Постников Е.А. и др. Моделирование и анализ финансовых рынков
Подождите немного. Документ загружается.

21
2.2. Расчет цены облигации как дисконтированного потока
платежей. Изменение цены облигации во времени.
Временная структура процентных ставок
Цена облигации является основным параметром при проведении
биржевых торгов. Как и для любого другого товара, рыночная цена об-
лигации определяется в результате взаимодействия спроса и предло-
жения. Для удобства цену облигации представляют в виде процента от
номинала.
Для расчета цены облигации используют метод дисконтирования,
то есть приведения потока платежей, генерируемого облигацией
, к те-
кущему моменту времени:
T
t
T
t
t
t
t
r
N
r
C
P
)1()1(
1
+
+
+
=
∑
=
, (2.1)
где
P
— цена облигации на момент размещения;
t
C
— купонный платеж в момент времени
t
;
N
— номинал облигации;
t
r — ставка дисконтирования;
T
— количество периодов до погашения.
Формула (2.1) позволяет рассчитать цену облигации на момент на-
чала обращения
0
=
t
, когда выплат по купонам еще не было. Упомя-
нутые в формуле периоды в реальности соответствуют году, полуго-
дию или нескольким месяцам. В российской биржевой практике пери-
од между выплатами для купонной облигации обычно составляет пол-
года (182 дня). Предположив, что количество периодов до погашения
равно четырем, мы можем проиллюстрировать, как изменяется
цена
облигации.
NCP
t
,,
0 1 2 3 4
N
2
C
3
C
4
C
1
C
t
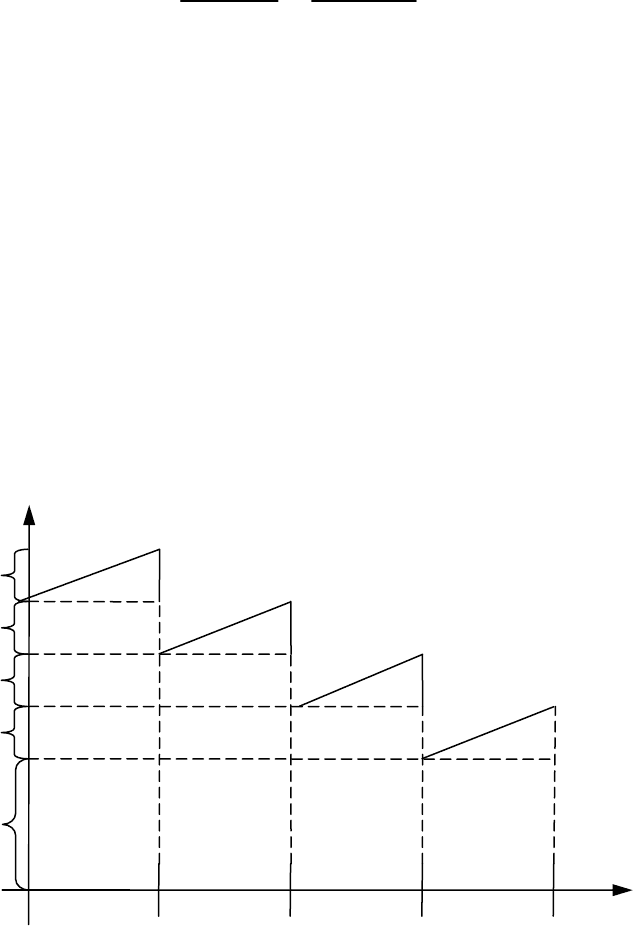
Рис. 2.2. Динамика стоимости облигации

22
По оси ординат обозначены четыре купона 4,1, =iC
i
и номинал
N
, а по оси абсцисс — время. Верхняя ломаная линия обозначает оста-
точную стоимость облигации. Действительно, в момент времени
0
=
t
эмитент не успел произвести ни одной выплаты и его обязательства со-
ставляют
NCCC +++
432
. Далее по мере приближения к дате пога-
шения первого купона
1=
t
цена облигации возрастает на
1
C
и падает
в момент выплаты купона и так далее.
В формуле (2.1) дисконтные множители
t
t
r )1(
1
+
уменьшают денеж-
ную оценку купона по мере его удаления от текущего момента време-
ни. Учитывая процесс изменения стоимости денег во времени, цена об-
лигации в начальный момент времени
0
=
t
будет стоить значительно
меньше, чем сумма всех обязательств эмитента. По мере приближения
к дате погашения она будет постепенно убывать.
Наиболее сложным моментом при оценке облигации по приведен-
ной формуле является определение процентных ставок
t
r
. Учитывая,
что
t
r
— ставка дисконтирования на период
t
, который может состав-
лять от нескольких месяцев до нескольких лет, нам обычно неизвестно,
какие факторы влияют на размер ставок и сохранятся ли они на преж-
нем уровне, скажем, через год или два. Есть несколько теорий, объяс-
няющих поведение ставок с различными периодами. Рассмотрим неко-
торые из них.
Теория ожиданий предполагает,
что будущие ставки являются не-
смещенными оценками действительных будущих ставок. Недостатком
теории ожидания является то, что она игнорирует риски, связанные с
инвестированием на более длительный срок.
Теория ликвидности учитывает компенсацию за риск при инвести-
ровании на более длительные сроки, причем эта компенсация возраста-
ет с увеличением срока до погашения, так как
увеличиваются риски.
Рис. 2.3. Временная структура процентных ставок
t
r
t
Премия за риск
23
Рассмотрим пример использования теории ожиданий и ликвидно-
сти (рис. 2.3). Для этого построим график временной структуры ставок,
отражающий их изменение во времени. По оси ординат обозначим до-
ходность, а по оси абсцисс время до погашения. Наличие фактической
возрастающей кривой в соответствии с теорией ожиданий говорит, что
в будущем следует ожидать повышения ставок
, однако в соответствии
с теорией ликвидности можно предполагать, что повышения ставок не
ожидается, а возрастающая кривая объясняется наличием премии за
риск.
2.3. Основные характеристики купонной
и бескупонной облигации. Методы расчета доходности
При обращении облигаций необходимо учитывать различные па-
раметры, среди них можно выделить такие, как накопленный купон-
ный доход (НКД) и доходность. Накопленный купонный доход состав-
ляет долю купона, которая подлежит выплате при совершении опера-
ций купли-продажи. Доходность представляет собой оценку выгодно-
сти вложения денежных средств в облигацию и может рассчитываться
различными методами: начиная от деления текущей рыночной цены на
номинал и заканчивая процедурой бутстреппинга.
Рассмотрим методику расчета НКД и доходности в соответствии с
методикой, принятой на бирже ММВБ.
Для расчета основных характеристик облигаций необходимо опре-
делиться с количеством дней в году и уметь рассчитывать количество
дней от одной даты до
другой. Во всех формулах расчета НКД и до-
ходности фигурирует так называемый базис — условное количество
дней в году (не путать со спрэдом между ценой фьючерса и базисного
актива). Под базисом можно понимать также методику расчета количест-
ва дней межу двумя датами. Так, если мы в качестве базиса используем
реальное количество дней
в году (этот базис обычно используется в рос-
сийской практике), то количество дней между датами мы берем фактиче-
ское. В случае с базисом 360, процедура расчета более сложная.
Можно выделить следующие наиболее часто используемые базисы.
Базис 365 (366). Основной базис, используемый на большинстве рос-
сийских бирж. Количество дней в году рассчитывается как разность
дат:
12
TTbasis
−
=
, (2.2)
где
21
, TT — первый и последний день в году.
Базисы 30/360. Существует три варианта базиса 30/360. Все вари-
анты используют формулу:

24
)(360)(30
121212
YYMMDDbasis −
+
−
+
−= , (2.3)
где
222111
..,.. YMDYMD — начальная и конечная даты.
− 30/360. Если
1
D приходится на 31 число, то
1
D меняется на 30.
Если
2
D приходится на 31 число и
1
D приходится на 30 или 31 число,
то
2
D меняется на 30.
− 30Е/360. Если
1
D приходится на 31 число, то
1
D меняется на 30.
Если
2
D
приходится на 31 число, то
2
D
меняется на 30.
− 30Е + /360. Если
1
D приходится на 31 число, то
1
D меняется на
30. Если
2
D приходится на 31 число, то
2
D меняется на 30 и
2
M уве-
личивается на 1.
Проще всего вычисляется доходность бескупонной облигации:
%100
100
××
−
=
t
basis
P
P
Y
, (2.4)
где
Y — доходность к погашению, в процентах годовых;
P
– цена облигации, в процентах от номинала;
t
– число дней от текущей даты до погашения.
Например, если цена облигации составляет 98,5 процентов, а число
дней до даты погашения 54, то доходность при погашении в процентах
будет рассчитываться следующим образом:
93,102100
54
365
5,98
5,98100
=××
−
=Y
.
Из формулы (2.4) можно легко получить цену облигации, задавая
доходность. Заметим, что для обеспечения положительной доходности
цена бескупонной облигации должна быть ниже номинала.
Расчет доходности купонной облигации выглядит несколько слож-
нее. Кроме того, существует несколько методик расчета доходности к
погашению купонной облигации.
Первым этапом при расчете доходности купонной облигации явля-
ется
расчет накопленного купонного дохода (НКД). Для этого обычно
используют линейную аппроксимацию купона, то есть предполагают,
что купонные выплаты равномерно распределяются между купонными
периодами.
0
0
TT
tTT
CA
C
C
−
−
−
×= , (2.5)
где
A
— накопленный купонный доход;
C
— текущий купонный платеж;
C
T — дата выплаты текущего купона;
0
T — дата выплаты предыдущего купона;
t
— количество дней до выплаты купона.

25
Заметим, что обычно в отличие от бескупонной, цена купонной
облигации обычно выше номинала за счет выплат по купонам.
Текущая доходность позволяет оценить годовую доходность ку-
понных выплат и рассчитывается следующим образом:
100×
×
=
P
D
basis
C
Y
t
t
current
. (2.6а)
Доходность к погашению можно вычислить, поделив поток дохо-
дов, генерируемый облигаций, на ее рыночную цену с учетом НКД:
1001
.
××
⎥
⎦
⎤
⎢
⎣
⎡
−
+
×
+
=
T
simplemat
D
basis
AP
TCN
Y
. (2.6б)
Эффективная доходность к погашению купонной облигации в про-
центах можно вычислить по следующей формуле:
basis
D
eff
T
mt
basis
D
eff
t
Tt
Y
N
Y
C
AP
)
100
1()
100
1( +
+
+
=+
∑
=
. (2.6в)
В формулах расчета доходности (2.6) приняты следующие обозна-
чения:
P
— цена облигации в процентах от номинала;
A
— накопленный купонный доход;
t
C — купонный платеж
t
;
N
— номинал облигации;
Y — доходность (эффективная) к погашению;
t
D
— количество дней до купонного периода t.
m — текущий купонный период.
T — количество купонных периодов.
Заметим, что эффективная доходность в силу сложности формулы
(2.6в) обычно вычисляется итерационным методом (процедура бутст-
реппинга) или методом перебора значений.
2.4. Чувствительность цены облигации к ставкам.
Дюрация Маколея
В предыдущем разделе мы рассмотрели, как меняется цена обли-
гации во времени: с момента размещения до погашения. Также пред-
ставляет интерес то, как меняется цена облигации в зависимости от
ставок на рынке. С такой «изменчивостью» цен облигаций связана тео-
рема «Об иммунитете облигаций», которая применима не только для
рынка облигаций, но
и может быть обобщена для произвольных обяза-
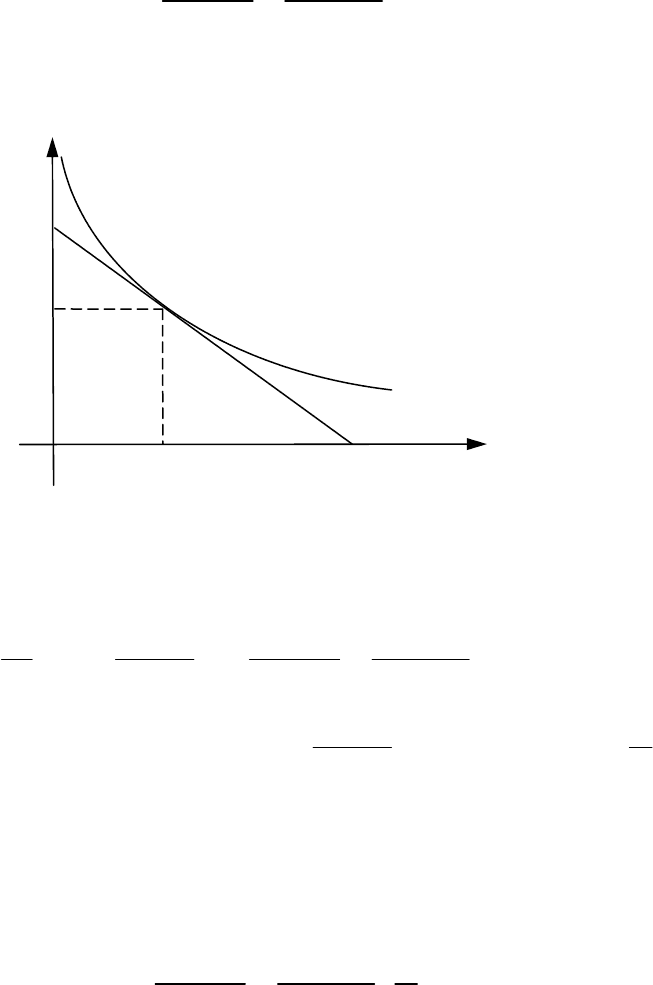
26
тельств и использоваться, в частности, в банковской сфере для созда-
ния сбалансированных кредитных портфелей.
Рассмотрим уже известную нам формулу определения цены обли-
гации в момент ее размещения (2.1). В качестве процентной ставки
можно взять некую средневзвешенную ставку
r
, что не повлияет на
точность определения цены облигации
P
. Тогда формулу можно пере-
писать следующим образом:
T
T
t
t
t
r
N
r
C
P
)1()1(
1
+
+
+
=
∑
=
. (2.7)
Меняя значения ставки
r
и определяя соответствующее им значе-
ние Р, можно построить кривую зависимости цены от ставки (рис. 2.4).
Рис. 2.4. Производная цены по ставке
Найдем производную цены
P
по ставке
r
.
⎥
⎦
⎤
⎢
⎣
⎡
+
+
+
+
−=
∂
∂
∑
=
T
T
t
t
t
r
tN
r
tC
r
P
r
)1()1(
)1(
1
1
. (2.8)
Производная (2.8) без выражения
)1(
1
r+
−
, умноженная на
P
1
, на-
зывается дюрацией Маколея (Macaulay Duration) и обычно обозначает-
ся MD. Фредерик Маколей в 1938 г. ввел эту величину и использовал в
качестве среднего времени инвестиций в облигацию вместо срока до
погашения:
P
r
tN
r
tC
MD
T
T
t
t
t
1
)1()1(
1
⎥
⎦
⎤
⎢
⎣
⎡
+
+
+
=
∑
=
. (2.9)
Кроме дюрации Маколея (2.9) часто используется модифициро-
ванная дюрация, которую можно рассчитать следующим образом:
r
0
r
0
P
P

27
P
r
tN
r
tC
r
D
T
T
t
t
t
if
1
)1()1(
)1(
1
1
mod
⎥
⎦
⎤
⎢
⎣
⎡
+
+
+
+
=
∑
=
. (2.9а)
Заметим, что при расчете как дюрации Маколея (2.9), так и моди-
фицированной дюрации (2.9а) в качестве ставки используется эффек-
тивная доходность к погашению (2.6в).
Частная производная цены по ставке представляет собой аппрок-
симацию изменения цены при изменении процентной ставки. Следова-
тельно, дюрация может быть использована для приближенного вычис-
ления изменения
цены облигации за счет изменения процентной ставки
на рынке.
Теорему об иммунитете облигаций можно сформулировать сле-
дующим образом. Риск изменения процентных ставок можно хеджиро-
вать, выравнивая дюрации активов и пассивов.
2.5. Пример расчета доходности облигации
с «плавающим» купоном
Расчет цены облигации с помощью рассмотренных нами формул
производится для конкретного денежного потока, все выплаты в буду-
щем являются фиксированными. Однако на практике эмитенты купон-
ных облигаций по различным причинам не фиксируют купоны, выпла-
ты по которым ожидаются через достаточно большой промежуток
времени. Известными являются один, два, или в лучшем случае
три
купона. Как же в таком случае рассчитывать цену или доходность?
Выход достаточно прост: неизвестные купоны принимаются равными
последнему известному.
Рассмотрим пример расчета доходности корпоративной облигации
ОАО «Челябинский трубопрокатный завод». С начала приведем неко-
торые данные о выпуске (табл. 2.1).
Таблица 2.1
Информация о выпуске
Показатель Значение
Номинал (р.) 1000
Дата начала размещения 22.06.2005
Дата окончания размещения 22.06.2005
Дата погашения 16.06.2010
Дней до погашения 1757
Периодичность выплат (в год) 2
Размер купона (% от номинала) 9,50
НКД (на 31.10.2005) 34,10

28
Окончание табл. 2.1
Показатель Значение
Рыночная цена (% на 31.10.2005) 102,20
Рыночная цена (р. на 31.10.2005) 1022,00
Доходность к моменту погашения (% год.) 8,55
Эффективная доходность к моменту пога-
шения (% год.) 9,10
Дюрация Маколея (дней) 1364
Модифицированная дюрация (лет) 3,43
Из приведенных данных рассчитываются такие показатели, как
купонный платеж, накопленный купонный доход, доходность к пога-
шению и дюрация. Проиллюстрируем расчет данных показателей.
Размер купона для конкретной облигации обычно приводится в
процентах от номинала. Купонный платеж в денежном выражении рас-
считывается как произведение годовой процентной ставки, приведен-
ной к 182 дням и умноженной
на номинал облигации:
3699,471000
365
182
100
5,9
=××=
t
C
.
НКД (2.5) рассчитывается следующим образом:
0959,30
05.06.2205.12.21
050622051031
1000
365
182
100
5,9
=
−
−
×××=
....
A
.
Здесь сначала ставка купонного платежа приводится к полугодо-
вому периоду, затем рассчитывается размер купона в денежном экви-
валенте и, наконец, полученное выражение умножается на коэффици-
ент, отражающий оставшееся количество дней до купонного платежа.
Отметим, что часто при расчетах для многих корпоративных облига-
ций период между купонными платежами составляет 182 дня, а
базис
365, что значительно упрощает расчеты, так как выплаты купонов по-
стоянно приходятся на один и тот же день недели.
Текущая доходность рассчитывается по формуле (2.6а).
100
1022
182
365
3699,47
×
×
=
current
Y
.
Расчет текущей доходности упрощается, если дана годовая купон-
ная ставка, в нашем случае 9,5 процентов:
100
5,102
5,9
×=
current
Y
.
Доходность к погашению для данной облигации рассчитывается
по формуле (2.6б) следующим образом:

29
5452,8100
1689
365
1
0959,341022
103699,471000
.
=××
⎥
⎦
⎤
⎢
⎣
⎡
−
+
×+
=
simplemat
Y
.
Проиллюстрируем расчет эффективной доходности (табл. 2.2).
Таблица 2.2
Расчет эффективной доходности
Купон-
ный пе-
риод,
t
Дата выплаты
купона
t
Дней до
выплаты,
t
D
Выплата,
t
C и
NC
t
+
в 10 период
Дисконтир.
t
C и
NC
t
+ в 10 период
1 21.12.2005 51 47,3699 46,7967
2 21.06.2006 233 47,3699 44,8074
3 20.12.2006 415 47,3699 42,9026
4 20.06.2007 597 47,3699 41,0788
5 19.12.2007 779 47,3699 39,3325
6 18.06.2008 961 47,3699 37,6604
7 17.12.2008 1143 47,3699 36,0594
8 17.06.2009 1325 47,3699 34,5265
9 16.12.2009 1507 47,3699 33,0588
10 16.06.2010 1689 1047,3699 699,8722
ИТОГО 1056,0952
Из таблицы видно, что в течение девяти купонных периодов эми-
тент облигации производит купонные выплаты, а в последний периоды
выплачивается купон и номинал. Для того чтобы рассчитать эффектив-
ную доходность, необходимо определить количество дней до выплаты
соответствующего купона
t
D , размер купона
t
C и затем дисконтиро-
вать полученный денежный поток по какой-либо начальной ставке с
учетом
t
D и базиса. Дисконтированные платежи складываются, и по-
лучается их приведенная стоимость (ИТОГО). Затем ставка изменяет-
ся, приведенная стоимость пересчитывается и так далее. Когда приве-
денная стоимость станет равной рыночной, мы найдем эффективную
доходность облигации. В результате выполнения итерационной проце-
дуры была установлена эффективная доходность в 9,1028 %. Для дан-
ной ставки можно
проверить соотношение (2.6в):
0948,1056
)
100
1028,9
1(
1000
)
100
1028,9
1(
3699,47
365
918251
10
1
)1(18251
=
+
+
+
=+
×+
=
−×+
∑
t
basis
t
AP
.(2.10)
Действительно, складывая рыночную цену и НКД, получаем чис-
ло, совпадающее с (2.10) до третьего знака после запятой:
0952,10560952,340000,1022
=
+
=
+
A
P
.
Таким образом, нами была действительно найдена эффективная
ставка доходности по рассматриваемой облигации.
30
Вопросы и задачи
1. Что такое облигация?
2. Выделите основные различия купонной и бескупонной обли-
гации.
3. Предприятию необходимо получить фиксированную сумму от
размещения облигационного займа. Какой способ размещения наибо-
лее предпочтителен для него?
4. Назовите основные теории временной структуры процентных
ставок.
5. Какой вид кривой процентных ставок (убывающая, возрастаю-
щая, «плоская») наблюдается сейчас
в России на рынке кредитования
физических лиц. Чем объясняется такая ситуация с точки зрения тео-
рии ожиданий?
6. В чем заключается теорема об иммунитете облигаций?
7. Рассчитайте НКД текущую и доходность к моменту погашения
для облигации ОАО «Челябинский трубопрокатный завод» для теку-
щей даты, приняв цену равной 103,60.
8. Рассчитайте эффективную
доходность к погашению для облига-
ции ОАО «Челябинский трубопрокатный завод» для текущей даты,
приняв цену равной 103,60 аналогично расчетам, приведенным в
табл. 2.2. Для этого можно воспользоваться электронной таблицей MS
Excel. По формуле (2.6) проверьте правильность расчета ставки эффек-
тивной доходности.
3. ФОРВАРД
3.1. Форвардный контракт
Одной из распространенных на практике производных ценных бу-
маг, позволяющих снизить риск, является форвард.
Форвардный контракт — это договор купли-продажи актива по
определенной цене исполнения k в определенный момент времени в
будущем T.
Покупатель форвардного контракта должен в момент времени T
оплатить определенное количество денег k за передаваемый ему другой
стороной
контракта актив.
Продавец форвардного контракта должен в момент времени T
передать актив другой стороне контракта и получить за него опреде-
ленное количество денег k.
