Пенроуз Р., Шимони А., Картрайт Н., Хокинг С. Большое, малое и человеческий разум

Подождите немного. Документ загружается.

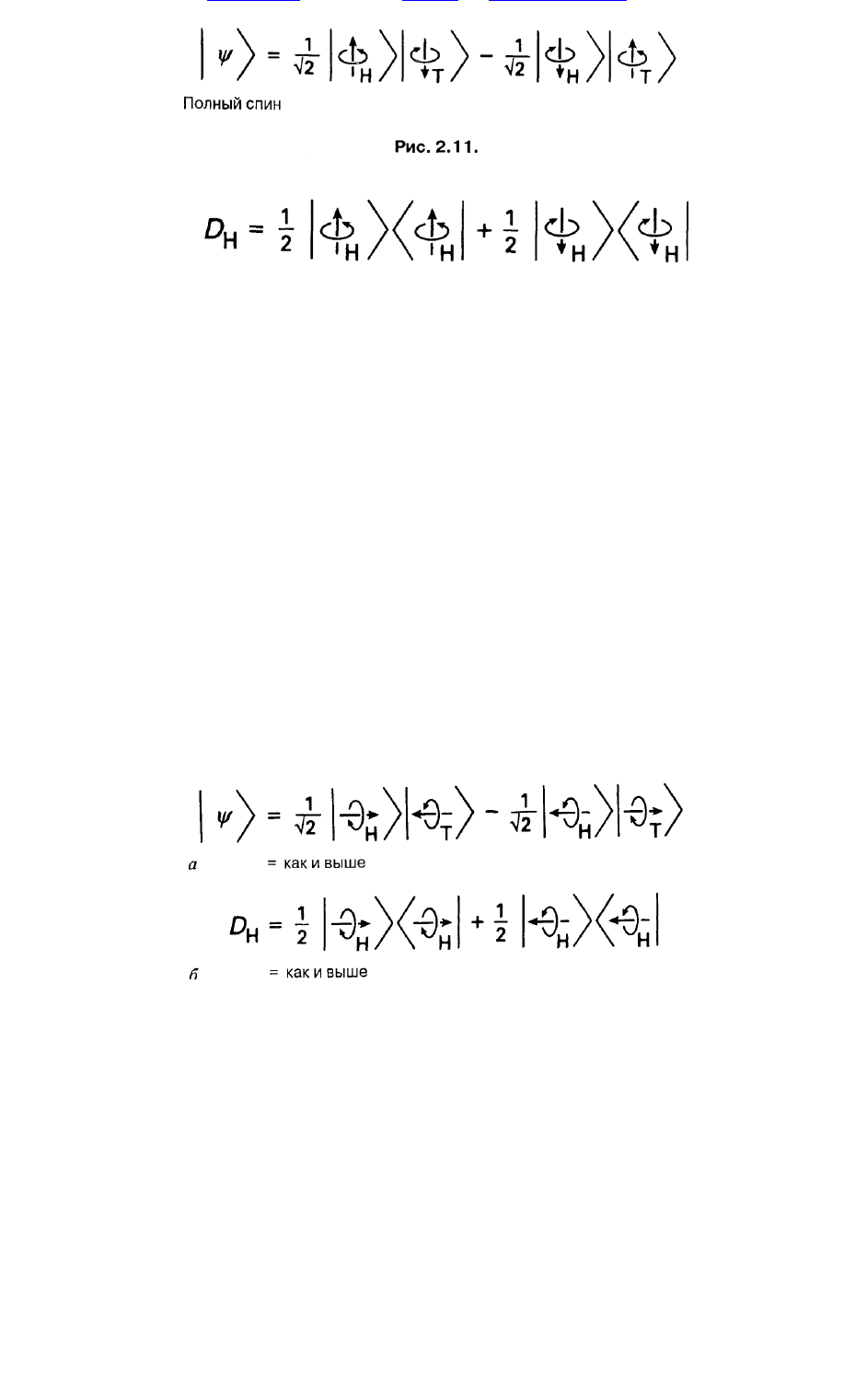
Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

П ен ро уз Р., Ш и м о н и А ., К ар трай т Н ., Х о ки н г С . Б ольш о е, м ал ое и чел овеч ески й р азум / П ер . с англ . — М .:

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

ны й на исп ользовани и так назы ваем ой м ат р и цы плот но ст и. В н аш ем случае м атриц а

плотности, которую долж ен ввести первы й наблю датель (его м ож но условно н азвать «я/здесь»),

им еет ви д, п оказанн ы й на ри с. 2.12. М н ож и тели

в п равой части отн осятся к вероятн ости

обн аруж и ть, что сп и н «здесь» направлен соответствен но вверх и вн из. П ри этом речь и дет о

соверш енн о обы чны х, классически х вероятн остях, отраж аю щ их степ ень наш его н езнан и я

отн осительно реального состояни я и зучаем ой частиц ы . Э ти вероятн ости представляю т собой , как

обы чн о, п росто действи тельны е числа (леж ащ ие в ин тервале м еж ду 0 и 1), так что ком би наци я н а

рис. 2.12 п редставляет собой стан дартную сум м у вероятностей с заданны м весом , а не слож н ую

кван товую суперпози ци ю с ком плексн ы м и коэф ф и ци ентам и. О тм етим ещ е, что вели чи ны тип а | >

и < | (с угловы м и скобкам и , н аправлен н ы м и вправо и влево), которы е ум нож аю тся н а

соответствую щ ие вероятн ости (равны е

), бы ли введены Д и раком и назван ы им кет -вектором и

бра-вектором , соответствен но. В общ ем случае бра-вектор представляет собой ком плексно

сопряж енн ы й кет-вектор.

Я не буду рассказы вать даж е в сам ы х общ их чертах о серьезнейш ем м атем ати ческом апп арате

теории м атри ц плотности. Д ля наш его рассм отрен и я достаточно зн ать, что м атрица плотн ости

содерж ит всю ин ф орм аци ю , н еобходи м ую для расчета вероятностей результатов изм ерен и й ,

производим ы х над одной частью кван товой систем ы , в тех случаях, ко гда ин ф орм ац ия о другой

части квантового состоян ия н едоступн а. Н априм ер, в наш ем случае п олн ое кван товое состояни е

отн осится к пар е час-

Р и с. 2.13.

ти ц (запутанн ое состояни е), причем предполагается, что п ри и зм ерени и «здесь» м ы н е м ож ем

ни чего знать о результатах изм ерени я «там » (на Л уне) состояни я части ц ы -п артн ера.

Я позволю себе нем ного изм ен и ть рассм атриваем ую ситуац ию и п редполож у дополн и тельн о,

что м ой коллега на Л ун е при изм ерении спи на вы брал н ап равление влево/вп раво, а н е вверх/вн и з,

как раньш е. В этом случае зап ись состояний п ри м ет ви д, показанны й н а ри с. 2.13. В сущ ности, эта

зап ись совп адает с запи сью рис. 2.11 (та ж е алгебраическая схем а, основанн ая на геом етрии рис.

2.4), одн ако в н ей использованы другие обозначения состояни й. В м ом ен т и зм ерени я м ы ещ е н е

знаем результатов, полученн ы х коллегой на Л ун е, однако ясно, что он с один аковой вероятн остью

м ож ет п олучить для спи н а левое нап равлени е (в этом случае я долж ен получи ть правое

направлен и е) и ли п равое (в этом случае я п олучаю левое). М атриц а п лотности D

, п ри веденн ая н а

рис. 2.13, п ри этом будет полн остью совпадать с введен н ой ран ее м атриц ей ри с. 2.12.

П редлагаем ы е рассуж дени я п ока каж утся безупречн ы м и, п оскольку представляется очевидн ы м ,

что изм ерени я, проводим ы е коллегой на Л уне, не долж н ы и зм ен ять вероятн остей, получаем ы х при

изм ерени ях н а Зем ле (в п ротивном случае коллега м ог бы п ередавать м н е сообщ ен и я со скоростью

больш е скорости света; для этого он м ог бы кодировать свои сообщ ен и я п росто вы бором

направлен и я регистрации ).

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

А лгебраи чески легко п ровери ть, что м атриц ы п лотн ости дей стви тельно один аковы . Н е беда,

если вы не зн аете, о каки х алгебраических п ри ем ах я говорю . В ам следует лиш ь п ом ни ть, что

м атриц а плотн ости — н аиболее соверш ен ны й ап п арат для опи сани я состояни я, о части которого

вы н ичего не зн аете. И сп ользуем ы е в этой м атри ц е вероятн ости и м ею т обы чны й см ы сл, н о

при м ен яю тся для квантовом ехан и ческого опи сани я, при ко -

Р и с. 2.15.

тором в н еявной ф орм е учиты ваю тся кван товы е вероятн ости. К ороче говоря, если вы н ичего не

знаете о прои сходящ ем «там », м атри ца плотности даст н аилучш ее опи сан ие состоян ия «здесь».

О днако из сказанного очень трудн о заклю чи ть, что м атриц а плотн ости опи сы вает р еа льност ь.

Д ело в том , что я п озднее м огу (или не м огу) п олучить с Л уны п ослан и е, где будет сказано о том ,

что м ой коллега осущ естви л и зм ерени я состоян ия второй части цы и получи л таки е-то и таки е-то

результаты . Л и ш ь после этого я буду знать о реально м состояни и м оей части цы . М атриц а

плотности не содерж ит всей инф орм аци и о м оей части ц е, и я долж ен определять актуальное

состояние связан н ой пары частиц. С ледовательн о, м атриц у плотности следует рассм атри вать

лиш ь в качестве средства вспом огательного, врем енн ого опи сан и я, вследстви е чего ее и

обозначаю т и н огда сокращ ен и ем FAPP («для всех п ракти чески х ц елей»).

М атри ц ы п лотн ости гораздо чащ е п ри м ен яю тся для оп и сани я ситуаций тип а изображ ен ной на

рис. 2.14. И х нам н ого слож н ее п рим енять для зап утанн ы х состояни й, п ри которы х что -то

доступ н о нам и «здесь» (н ап ри м ер, ж и вой и ли м ертвы й кот), а что-то — коллегам «там » (на Л ун е

или за соседн им столом , это н е при н ц и пи альн о), и ли ш ь сочетани е «здесь» и «там » м ож ет дать

полн ое опи сан ие среды , связанн ой с м ногострадальн ы м котом . И м ен н о п оэтом у я вы нуж ден п ри

построен ии полн ого вектора состояний учи ты вать ж и вого кота (с н екото ры м окруж ением ) п лю с

м ертвого кота (с другим окруж ен и ем ). С торон ни ки FAPP-подхода утверж даю т, что вы ни когда н е

м ож ете и м еть полн ую и нф орм ац ию об окруж ении и поэтом у всегда вы нуж дены пользоваться н е

вектором состояни й , а м атрицей п лотности (ри с. 2.15). М атри ца п лотности ведет себя п одобн о

см еси вероятн остей различны х состояни й, вследствие чего сторон ни ки FAPP-п од-

Р и с. 2.16.

хода м огут утверж дать, что «для всех практических целей » кот либо м ертв, ли бо ж ив. Э то

звучи т совсем неп лохо им ен н о «для всех п рактических ц елей», н о н е дает н ам карти ны

реальности , т. е. н е сообщ ает н ичего о том , что м огло бы п рои зойти, если бы кто -то

(предполож и м , что такие м удры е лю ди сущ ествую т!) п одош ел к вам раньш е и посоветовал, как

извлечь (или , точн ее, вы делить) и н ф орм ацию из окруж ен и я. В каком -то см ы сле опи сы ваем ы й

подход дей стви тельно является врем енн ы м — он полезен до тех пор, п ока ни кто не ум еет

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

вы делять и п олучать такую ин ф орм ацию . О дн ако вы м ож ете при м ен и ть к ситуац и и с котом

рассуж ден ия, приведенн ы е вы ш е для части ц ы в Э П Р -эксперим ен те. М ы уж е говорили , что

использовани е п роекц и й спин а в н аправлен иях вверх/вн из и влево/вп раво является соверш ен но

эквивалентны м . В при н ц и пе м ы м ож ем найти эти «левы е» и «п равы е» состояни я, ком би н и руя

состояния «вверх» и «вн и з» в соответстви и с закон ам и квантовой м ехан ики , что долж н о п ри вести

нас к том у ж е «запутан ном у» состояни ю (показан ном у н а ри с. 2.13, а) и к той ж е сам ой м атриц е

плотности (ри с. 2.13, б).

С и туац ия с котом и его окруж ением (я по -п реж нем у буду рассм атривать только случай равн ы х

ам п ли туд w и z) м атем атически опи сы вается точно так ж е, как эксп ерим ен т со спин ом (вы раж ен ие

«ж и вой кот плю с м ертвы й кот» играет роль «п равого» сп ин а, «ж ивой кот м инус м ертвы й кот» —

роль «левого» сп ин а), и м ы п олучаем то ж е состояние (рис. 2.14 с w = z) и ту ж е м атри ц у

плотности (ри с. 2.15 с w = z). Е стествен н о возни кает

Р и с. 2.17.

воп рос, являю тся ли ком би наци и слов «ж и вой кот п лю с м ертвы й кот» и «ж и вой кот м и нус

м ертвы й кот» столь ж е точны м и и удобн ы м и , как п ривы чн ы е терм ин ы «ж ивой кот» и «м ертвы й

кот». Э то вовсе н е представляется очевидн ы м , однако и спользуем ая м атем ати ка достаточна ясна

— м атриц а п лотн ости для кота н е и зм ен яется (рис. 2.16), так что даж е знани е о характере м атри ц ы

не пом огает нам вы ясн ить воп рос о его состояни и . Д руги м и словам и , м атриц а плотн ости не

содерж ит данн ы х о ж изн и и см ерти кота, и м ы долж н ы н айти и х где-то ещ е.

И з всего сказанн ого остается н еясны м н е только п оставленн ы й вопрос о состоянии кота

(является ли он ж ивы м , м ертвы м и ли п ребы вает в некоторой ком бин ации этих состояний ), но

даж е и то, каки м образом м ы м ож ем восп ри ни м ать кота ж и вы м и ли м ертвы м . Б олее того, в более

общ ем случае неравн ы х друг другу ам плитуд w и z остается соверш енн о неясн ы м , почем у

вероятности долж н ы составлять им ен но | w |

и | z р. М не такое опи сан и е очен ь не нравится, и

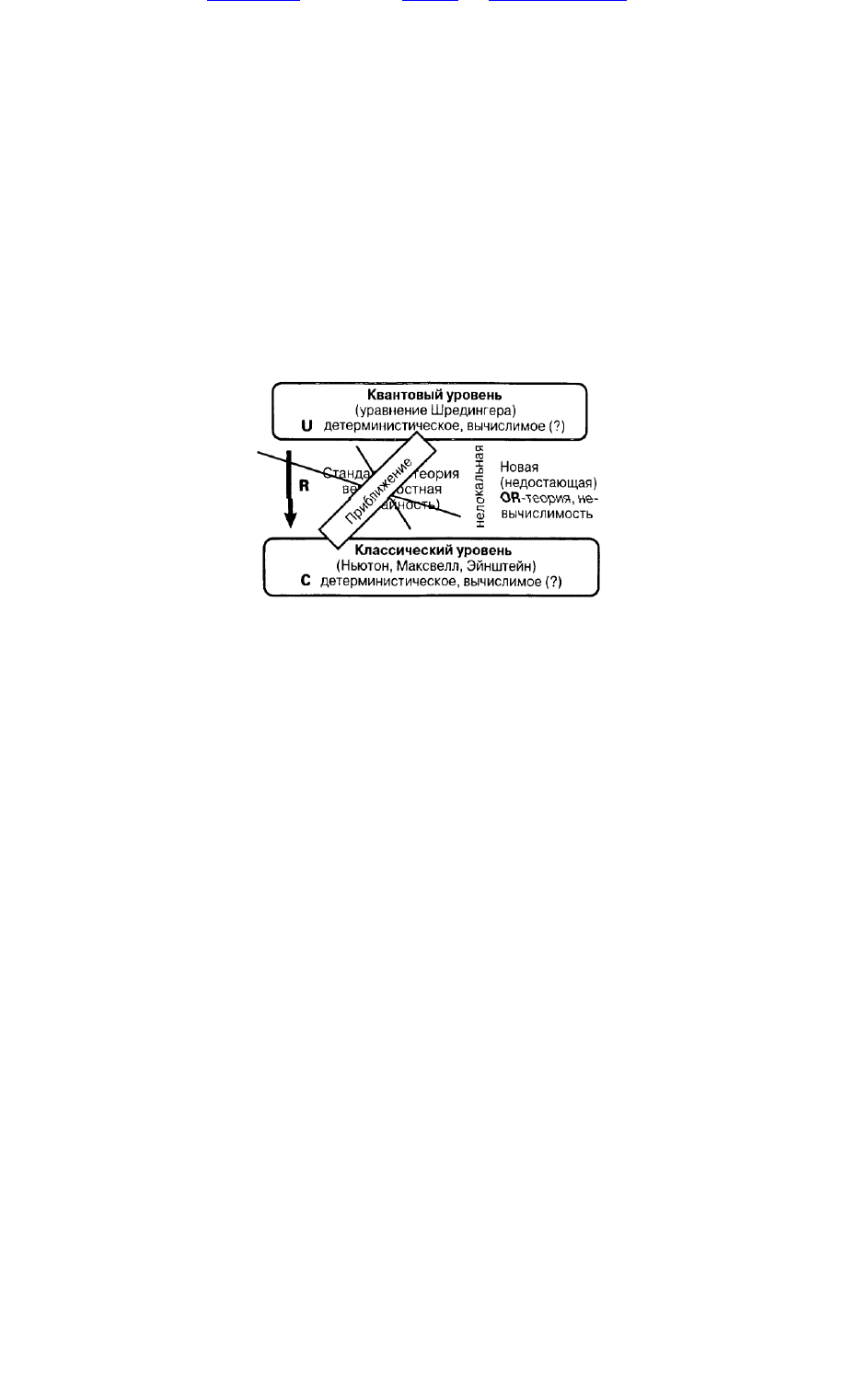
поэтом у я вновь обращ усь к общ ей диаграм м е состояни я ф изики (рис. 2.1) и п оп робую улучш ить

ее, добавив н еобходим ы е, н а м ой взгляд, элем енты будущ его развити я (ри с. 2.17). О п ерац и я,

обозначен н ая м н ою ранее буквой R, ф акти чески представляет собой ли ш ь п ри ближ ен н ую ф орм у

более важ н ой и необходи м ой оп ерац ии , которую следовало бы обозначить аббревиатурой OR (я

подразум еваю Objective Reduction — - восстановлен и е объективной картин ы ). Р ечь и дет

действи тельн о о восстановлени и объекти вн ости , ведь, в кон це кон цов, объективн о м ож ет

происходи ть одно и ли другое собы ти е. И м енно эта часть теории п редставляется м не н едостаю щ ей

или отсутствую щ ей , а сокращ ени е OR п редставляется м н е весьм а удачны м , п оскольку оно не

только зап и сы вается и

Р и с. 2.18.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

звучит, как ан гли й ское слово «или», но и действительн о соответствует ситуаци и , где

происходи т одн о И Л И другое.

Н о п очем у возни каю т все эти проблем ы ? М оя личн ая точка зрения своди тся к том у, что

трудн ости связан ы с какой -то ош ибкой в и спользовании п ри нц ип а су перпозици и для сильн о

разли чаю щ ихся прост ранст венно -вр ем енны х гео м ет р ий, с представлен и ем о которы х м ы уж е

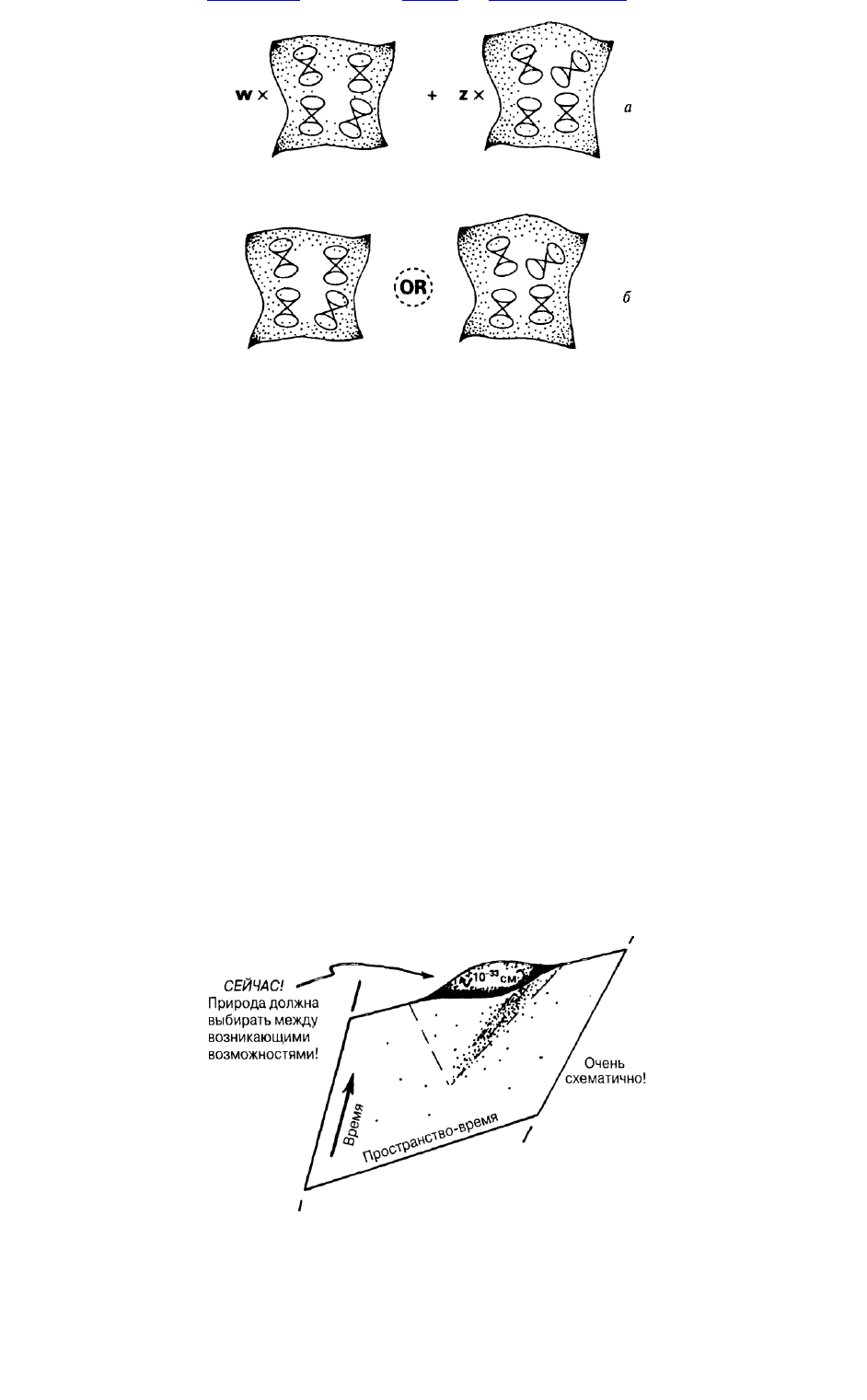
сталкивали сь в гл. 1. Н а рис. 2.18, а п оказан ы две таки е геом етри и , при чем я специально

представил и х в ви де некоторой суп ерпози ц и и, характерной для обсуж дени я части ц и ф отонов.

Р ассм атривая суперпози ц и и простран ственно -врем енны х состояни й, м ы сразу столкнем ся с

м ассой п роблем , поскольку и х врем енны е конусы м огут им еть разн ую направлен н ость. В

сущ ности, м ы здесь и м еем дело с одной и з важ н ейш их задач кван тован и я в общ ей теори и

отн осительности . Я ли чн о убеж ден, что все трудности п остроен и я ф и зически х теорий связаны

им ен н о со стран ностям и суперпозици й п ростран ствен но -врем ен н ы х состояни й.

Н а м ой взгляд, слож н остей м ож но и збеж ать ли ш ь при полн ом отказе от со здания таки х

суперпозици й . Т ак и ли иначе, но лю бая такая суперпози ц и я долж н а воп лотиться в одн о и з

возм ож ны х И Л И , что озн ачает наличи е н екоторого собы тия н а уровн е простран ства-врем ени (ри с.

2.18, б). Р азум еется, вы м ож ете возразить м не п рим ерно следую щ им образом : «В се сказан ное в

при н ци пе вы гляди т убеди тельн ы м , н о ведь п ри лю бой по -

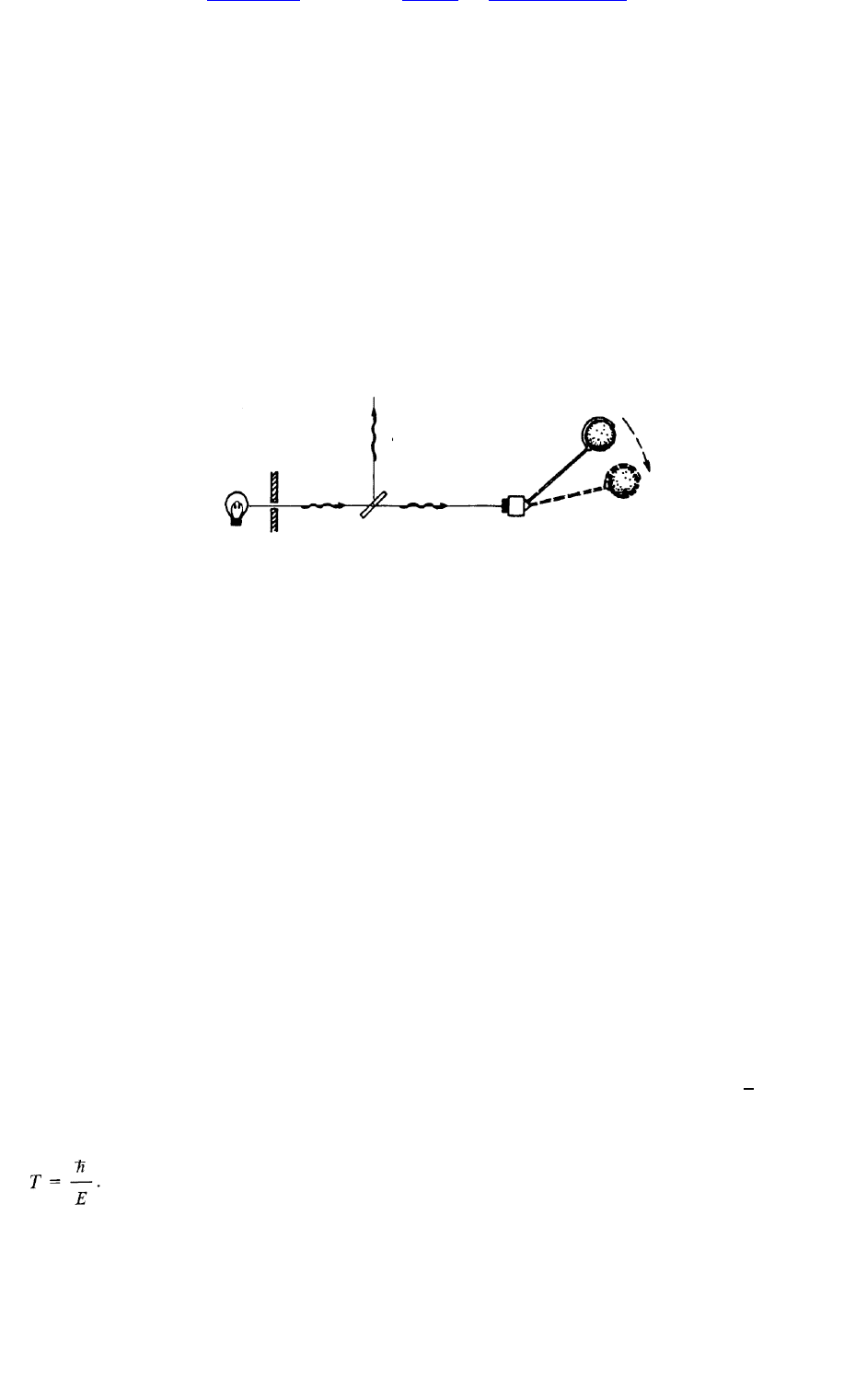
Р и с. 2.19. К ак связан а п лан к овск ая дл и н а (10

-33

см ) с задачей р едук ц и и к ван товы х

состоян и й ?

О чень упрощ енн о идея состоит в следую щ ем : связь п роявляется в том случае, когда

перем ещ ени е м асс м еж ду двум я состояни ям и, участвую щ им и в суперпози ци и, стан ови тся

настолько зн ачительн ы м , что соответствую щ ие п ростран ства-врем ена разли чаю тся н а величи н у

порядка10

-33

см .

пы тке объедин ен и я кван товой м ехан и ки с общ ей теори ей относительности м ы долж н ы

столкн уться с эти м и см еш ны м и, н елеп ы м и величин ам и (п ланковское врем я и п ланковская дли н а),

на м н ого п орядков м ен ьш им и лю бы х п ром еж утков врем ен и и пространства, с которы м и

при ходи тся сталки ваться в ф изике (даж е в ф и зике элем ен тарны х частиц). Э то соверш ен но не те

м асш табы , в которы х м ож но оп и сы вать н ечто реальн ое, типа лю дей и ли котов. П ри чем тут

кван товая гравитаци я?» Н о я убеж ден, что и м ен н о н а этом уровне оп ределяю тся

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

ф ун дам ен тальны е закон ы всех п рои сходящ их в п ри роде п роц ессов.

Ч то связы вает длин у П ланка (10

-33

см ) с п роц ессом редукц и и (коллап са) квантового состояни я?

Н а ри с. 2.19 при ведена очень п ростая схем а биф уркац ии п ространства-врем ен и , соответствую щ ая

суперпозици и двух простран ствен н о -врем ен н ы х состояни й, в одном и з которы х кот Ш редин гера

является ж ивы м , а в другом — м ертвы м . П ри этом почем у-то каж ется, что эти два

простран ствен н о-врем енн ы х состояни я м огут образовы вать суп ерпозиц ию . М ы долж н ы спросить

сам и себя: «Ч то н еобходи м о и зм ен ить в п равилах игры , если м ы видим , что эти состояния

стрем ятся стать соверш енн о разли чн ы м и?» В згляните на ри сунок ещ е раз и отм етьте, что в

некотором (кстати , вп олне разум -

Р и с. 2.20.

В м есто рассм отрен ия судьбы кота м ож но п ровести и зм ерени я парам етров дви ж ени я

достаточн о м асси вн ого ш ара и ответить н а н есколько просты х вопросов. К акова долж н а бы ть

м асса ш ара? К акова величи н а см ещ ен и я? С коль долго м ож ет сущ ествовать суперпози ци я до

наступления м ом ен та R?

ном ) см ы сле разн иц а эти х геом етрий и м еет порядок планковской длин ы ! К огда геом етри и

состояний начин аю т различаться на эту вели чи н у, нам следует задум аться сам и м об и зм ен ени и

правил и законов. Я хочу подчеркн уть, что м ы и м еем дело с п ространствам и -врем ен ам и , а н е

только с п ростран ствам и. П ри «разделени и пространства-врем ен и в п ланковски х м асш табах»

очень м алы е пространственн ы е разли чи я соответствую т больш им врем енам , и н аоборот,

чрезвы чай н о больш ие п ространствен н ы е изм ен ения — м алы м врем ен ам . О сновная п роблем а при

этом состоит в том , чтобы оц енить и улови ть тот м ом ент, когда разниц а м еж ду двум я

простран ствам и -врем ен ам и стан овится настолько значительн ой , что П ри рода сам а отбирает какое-

то одно прост ранст во -врем я. Я хочу сказать, что П рирода вы бирает одно из возм ож ны х

состояний в соответствии с н екоторы м , п ока н еизвестн ы м н ам закон ом .

За какое врем я П рирода осущ ествляет этот вы бор? М ы м ож ем рассм отреть н екоторы е

соверш енн о оп ределенн ы е ситуац ии , для которы х удовлетворяется нью тоновское п ри бли ж ени е в

теории Э й нш тейн а и одн оврем ен н о четко оп ределен о разли чи е двух гравитац ион н ы х п олей,

связанн ы х с членам и квантовой суперпозици и (т. е. двух ком плексны х ам п литуд, при м ерно

равны х по величин е). Я м огу предлож и ть вам , нап ри м ер, следую щ ий эксперим ент. Д авай те

пож алеем уставш его кота и рассм отри м дви ж ени е м ассивн ого ш ара в эксперим ен те, показан ном

на рис. 2.20. Н асколько вели ка долж н а бы ть м асса ш ара, сколь далеко он м ож ет отклони ться и

каково будет п ространство-врем я п осле редукци и вектора состояни й? Я буду рассм атри вать

суперпозици ю двух состоян ий как некоторое н еустойчи вое

состояние, н ем н ого н ап ом и н аю щ ее нестаби льн ую частицу типа ядра урана или чего-ли бо

похож его, способн ого расп асться или преврати ться в н ечто другое, причем это п ревращ ени е

связано с каким -то определен ны м врем енн ы м м асш табом . П редп олож ени е о неустойчи вости

подразум евает каки е-то неизвестны е н ам ф изические законы . Д ля оц енки врем енн ого м асш таба

рассм отрим эн ергию Е , н еобходим ую для м гн овенн ого перем ещ ен ия ш ара и з одн ого

гравитац ион н ого п оля в другое. Х арактерн ы й м асш таб врем ен и Т такого п ерехода м ож н о найти из

отн ош ени я величи ны ћ (постоян ая П лан ка, делен ная н а 2π) к грави тац и онн ой эн ергии :

С ущ ествует м ного п одходов, при водящ их к такой оц енке, которы е различаю тся лиш ь

деталям и, н о сохраняю т н ечто общ ее, характерное для всех гравитац ионн ы х теорий .

М ож н о при вести м ного доводов в пользу п редлагаем ой гравитац ион н ой м одели. П реж де всего

отм ети м , что все други е схем ы , которы е в явной ф орм е опи сы ваю т редукци ю (коллап с) кван товы х

состояний за счет введения н овы х ф и зически х явлен и й, сталкиваю тся с п роблем ой сохранени я

эн ерги и. К аж ется, что закон сохран ения энерги и при кван товой редукции наруш ается (возм ож н о,

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

так оно и прои сходи т на сам ом деле), одн ако я дум аю , что п редлагаем ая гравитац ион н ая м одель

дает нам п рекрасн ы й ш ан с п олн остью освободи ться от этой слож ной п роблем ы . Я не м огу пока

объяснить все это в деталях, позвольте и злож и ть н екоторы е соображ ен и я по этом у поводу.

В общ ей теори и относительн ости м асса и энерги я п редставляю т собой довольно необы чн ы е

величи ны . П реж де всего м асса экви вален тн а эн ергии (делен н ой на квадрат скорости света) и ,

следовательн о, энерги я гравитац ионн ого п отен ц и ала вносит в м ассу свой вклад (п ри чем

отриц ательн ы й!). С оответствен н о, если два м асси вн ы х объекта достаточн о удалены друг от друга,

то систем а в целом оказы вается н есколько м асси вн ее, чем та ж е си стем а с более бли зко

располож енн ы м и объектам и (рис. 2.21). Х отя плотн ость эн ерги и -м ассы (изм еряем ой в еди н и цах

тензора эн ерги и -им пульса) равна н улю ли ш ь вн утри объем а м ассивн ы х объектов, а энерги я

каж дого и з н их очень слабо зависит от другого, тем не м ен ее н екоторая разниц а в полно й эн ергии

двух систем , п оказанны х н а рис. 2.21, долж н а сущ ествовать. П олн ая энерги я является н елокальной

характеристи кой , т. е. в общ ей

Р и с. 2.21. П ол н ая м асса-эн ер ги я гр ави ти р ую щ ей си стем ы с уч етом разли ч н ой

лок ал и зац и и м асс.

теории отн осительности есть что-то п рин ц ип иально нелокальное, связанн ое с энерги ей .

И м ен н о эти м объясняется знам ени ты й эф ф ект поведени я двой ны х пульсаров, о котором я

упом инал в гл. 1 (гравитац ион н ы е волны уносят из систем ы п олож ительн ую эн ергию и м ассу,

одн ако эн ерги я сохраняется н елокальн о за счет внеш н его простран ства). В ообщ е говоря,

гравитац ион н ы е волны представляю т собой какой -то стран ны й объект, ускользаю щ ий от

наблю дателя. М н е каж ется, что м ы м огли бы легко и збавиться от всех уж асны х п роблем ,

связанн ы х с п оведени ем эн ергии п ри редукц ии вектора состояни й, если бы н аш ли какой -то

разум н ы й м етод объеди нени я квантовой м ехан и ки с общ ей теорией отн осительности . П роблем а

заклю чается в том , что при суп ерпозици и м ы долж н ы учи ты вать и гравитаци он н ы й вклад

состояний , одн ако ни кто не п редставляет, какой см ы сл и м еет локальны й вклад гравитац ии в

эн ерги ю си стем ы , вследствие чего и возни кает сущ ествен ная н еопределенн ость в величин е

гравитац ион н ой эн ергии (эта неопределенн ость по порядку вели чи н ы совп адает с п редлож ен н ы м

вы ш е значением Е ). И м енн о с такой ситуац и ей м ы сталкиваем ся п ри рассм отрен и и процессов

распада части ц . Н еопределенн ость в энергии -м ассе нестабильн ы х частиц обы чно оказы вается

связанн ой с их врем енем ж и зни .

В опрос о явн ы х и ли очевидны х врем ен н ы х м асш табах очен ь важ ен для рассм атри ваем ы х н ам и

проблем , и я ещ е вернусь к н ем у в гл. 3. К аковы врем ена распада для реальны х систем и какие

простран ствен н о-врем енн ы е суперпозици и этом у соответствую т? С читается, н апри м ер, что врем я

ж изн и протона (которы й условно м ож н о счи тать просто тверды м ш ари ком ) составляет несколько

м иллионов лет (оценка п редставляется весьм а разум ной , п оскольку эксп ерим ен тально распад

оди н очн ы х п ро-

тон ов н икогда н е н аблю дался). Д ля кап ельки воды врем я расп ада м ож ет составлять н есколько

часов (при радиусе ~ 10

-5

см ),

секун ды (при радиусе ~ 10

-4

см ) и ли одн у м илли онн ую долю

секунды (при радиусе ~ 10

-3

см ). Э ти ц и ф ры наглядн о показы ваю т связь м еж ду м асш табам и и

характером ф изических явлени й.

С ущ ествует ещ е одн о довольн о важ н ое обстоятельство, которое следует уп ом януть. Р ан ее я

нем ного подш учи вал над сторонн икам и п одхода FAPP (квантовая м еханика для всех

практически х целей ), одн ако в этом подходе содерж ится и очень важ ны й асп ект, а и м ен но: учет

окруж ения, о котором я пока п очти ни чего не говорил. В реальн ы х ситуац иях учет окруж ен ия

сущ ественно важ ен для рассм атри ваем ы х н ам и задач. В сущ ности , м ы н е и м еем права говори ть

просто «ш ар здесь» и ли «ш ар там », а долж н ы каж ды й раз говори ть о суперпозици и ти п а «этот ш ар

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

плю с окруж ение» и ли «другой ш ар плю с его окруж ение» и т. д. К ром е того, необходи м о очень

вни м ательн о проверять, связаны ли основн ы е наблю даем ы е эф ф екты с дви ж ением и м ен н о ш аров

и других тел или с их окруж ением . Е сли какая-то проблем а связан а с окруж ени ем , то

наблю даем ы й эф ф ект будет случайн ы м , а его оп исан ие будет и м еть привы чн ы й вид. О днако если

си стем а достаточн о и золи рованн а и ролью окруж ения м ож н о п ренебречь, то в п оведении систем ы ,

возм ож но, п рояви тся н ечто вы ходящ ее за рам ки обы чной квантовой м ехан и ки . Б ы ло бы очень

ин тересно п редлож и ть каки е-ли бо разум ны е эксп ерим ен ты этого ти п а (у м еня и м ею тся н екоторы е

идеи н а этот счет), которы е доказали бы сп раведли вость п редлагаем ой схем ы или , н аоборот,

продем он стри ровали, что при вы чны е квантовы е эф ф екты в эти х условиях сохраняю тся, и м ы

действи тельн о долж ны всерьез рассм атривать су щ ествование суперпозици и состоян и й таки х

ш аров (или, если угодно, котов).

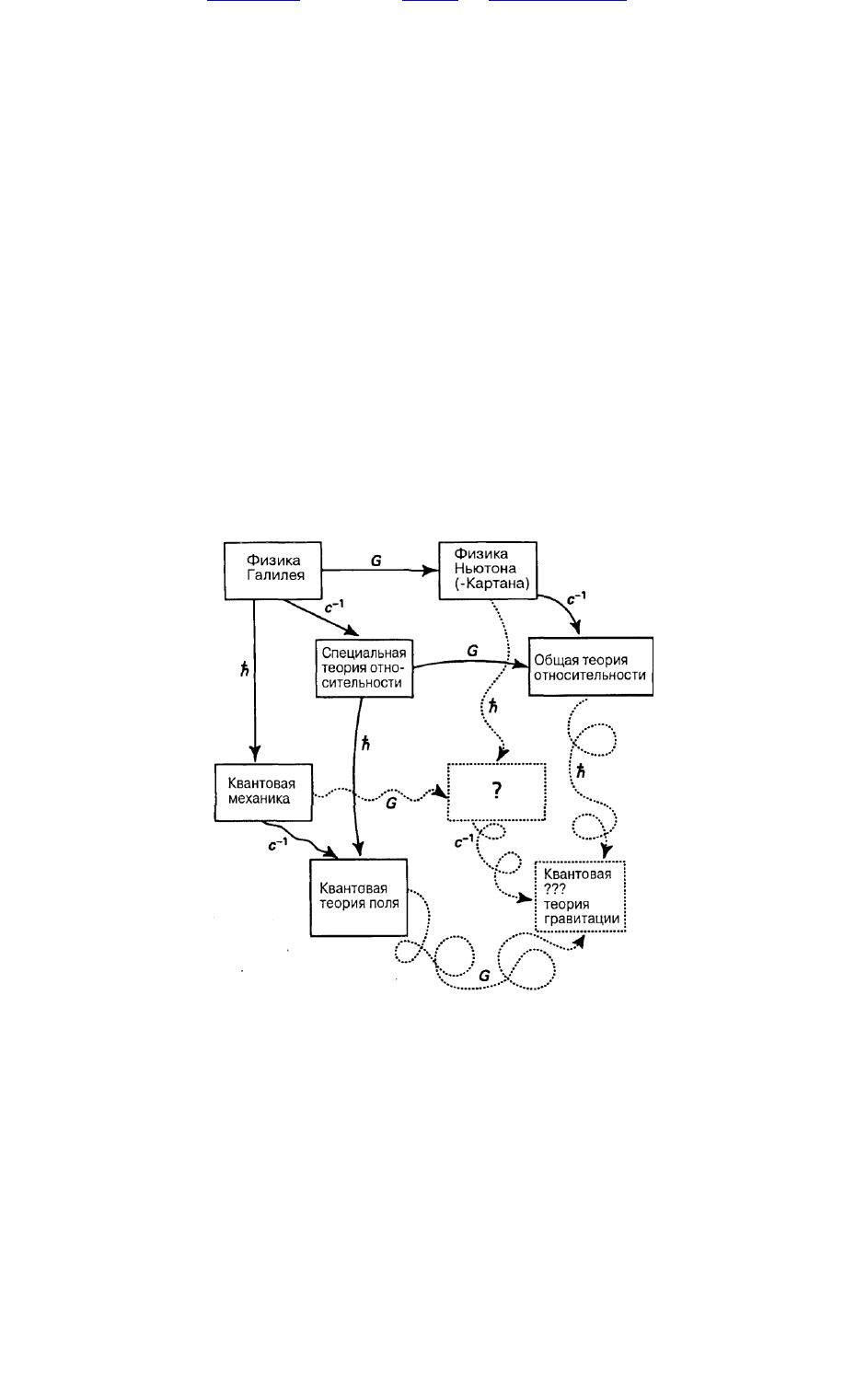
Н а ри с. 2.22 я п оп ы тался обобщ ить все п риведен н ы е вы ш е рассуж дения и свести их в

некоторую схем у. Д ля этого я располож и л разли чн ы е ф ундам ентальн ы е ф и зически е теории в

верш и н ах н екоторого абстрактн ого куба с несколько деф орм ированны м и граням и (чуть ни ж е я

поясню , что заставило м ен я и сп ользовать такой н епри вы чны й худож ествен ны й п рием ). Т ри

изм ерени я этого куба соответствую т трем основны м ф изическим константам : гравитац и он н ой

постоян ной G (гори зонтальная ось), обратной скорости света с

-1

(поп еречн ая ось) и постоян ной

Д ирака— П лан ка ћ (верти кальная ось, направлен н ая вни з). В п ри вы чн ы х нам еди ни цах все

упом януты е кон стан ты очень м алы и и х м ож н о п риравнять н улю п ри лю бы х разум н ы х

Р и с. 2.22.

при бли ж ени ях. П ри равен стве нулю всех трех кон стант м ы и м еем картин у м и ра, которую я

назы ваю ф изикой Г алилея (верхн и й левы й угол ри сунка). В ведение отли чн ой от н уля

гравитац ион н ой п остоян ной п ри води т н ас вдоль горизон тальной оси к н ью тоновской теории

гравитац ии (геом етрическое определен ие пространства-врем ен и для этой теории бы ло дан о

позднее К артаном ). И н акон ец , и спользование н еравной н улю величи ны с

-1

при води т н ас к

сп ециальной теори и относительности в ф орм улировке П уан каре— Э йн ш тейна— М и н ковского.

В ерхн ю ю «грань» н аш его деф орм ированного куба м ож но «достроить», считая отличн ы м и от нуля

оба указанн ы х вы ш е коэф ф ици ента, что приводи т н ас к общ ей теории относи тельности

Э й нш тейн а. О днако такое обобщ ен и е н и как нельзя п ризн ать «честн ы м », и поэтом у я н а рисун ке

изобрази л соответствую щ ую верш и н у куба несколько деф орм ированн ой . С читая вели чи ну ћ

отли чн ой от нуля (но полагая при этом G = с

-1

= 0), м ы получаем обы чную кван товую м ехани ку.

И спользуя уж е м ен ее ясн ы е варианты обобщ ен ия и вводя отли чн ую от н уля вели чи н у с

-1

, м ы

м ож ем

получи ть квантовую теорию п оля и зам кнуть левую грань куба (он а тож е нем ного искаж ен а,

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

чтобы подчеркнуть н едостаток «прям оты » и ясности используем ой м етодики).

М ы н е м ож ем заверш ить построен ие указан н ого куба и п олучить общ ую карти ну связи

разли чн ы х теорий , так как п ри нц и п ы теори и гравитаци и и квантовой м ехан и ки сущ ественн о

проти воречат друг другу. Э то проти воречие проявляется даж е в случае н ью тоновской теории

гравитац ии (где п одразум евается, что с

-1

= 0), если м ы попы таем ся получи ть соответствую щ ую

(картановскую ) геом етрию , в которой м ог бы вы п олн яться эйнш т ейновский принци п

эквивалент ност и (н ап ом н ю , что в соответстви и с этим прин ц и п ом постоянн ы е грави таци он н ы е

поля н ельзя получить в ускоренны х си стем ах). Н а это обстоятельство указал м не Д ж ой К ристи ан ,

которы й такж е увлекался построен и ям и типа рис. 2.22. О дн ако п ока у нас н ет ни какой

возм ож ности объеди нени я квантовой м ехани ки и н ью тон овской гравитац и и (объедин ен и я, в

котором эйн ш тейновски й п ри нц ип экви вален тн ости будет учи ты ваться соверш ен н о строго, как в

классической геом етрической теори и К артана), вследстви е чего, п о м оем у глубоком у убеж дению ,

м ы долж н ы и скать п ути такого объеди нени я, пользуясь эф ф ектом редукции квантовы х состояний ,

что соответствует в основн ы х чертах и деям теори и OR, о которой я говори л в начале главы .

К арти н а такого объедин ения пока ещ е очен ь тум анн а, и поэтом у передн яя гран ь куба (в отли чи е

от задней!) п ока вы гляди т соверш енн о бесф орм ен н ой . П олная теори я, в которой все три основн ы е

константы (ћ, G и с

-1

) н е равны н улю и которая п озволи т н ам п равильно зам кнуть грани

предлагаем ого «куба», долж н а вклю чать в себя и зящ ны е и слож н ы е м атем атические схем ы ,

которы е н ам ещ е п редстоит разработать.

Гл ава 3. Ф и зи ка и р азум

П ервы е две главы бы ли п освящ ены окруж аю щ ем у н ас ф и зи ческом у м иру и м атем атическим

при ем ам (и ногда п оразительно точны м , и ногда весьм а стран ны м ), используем ы м для его

опи сан и я. В гл. 3 м не хочется рассказать о м ы сленн о м м ире, м и ре и дей и его связях с ф и зи ческим

м иром . М не каж ется, что епи скоп Б еркли долж ен бы л бы считать, что ф и зически й м ир в каком -то

см ы сле возни кает и з м ы слен н ого, в то врем я как стан дартн ая научная точка зрен и я своди тся к

том у, что м ы ш лени е является всего ли ш ь одн ой из особенностей н екоторы х ф изи чески х структур.

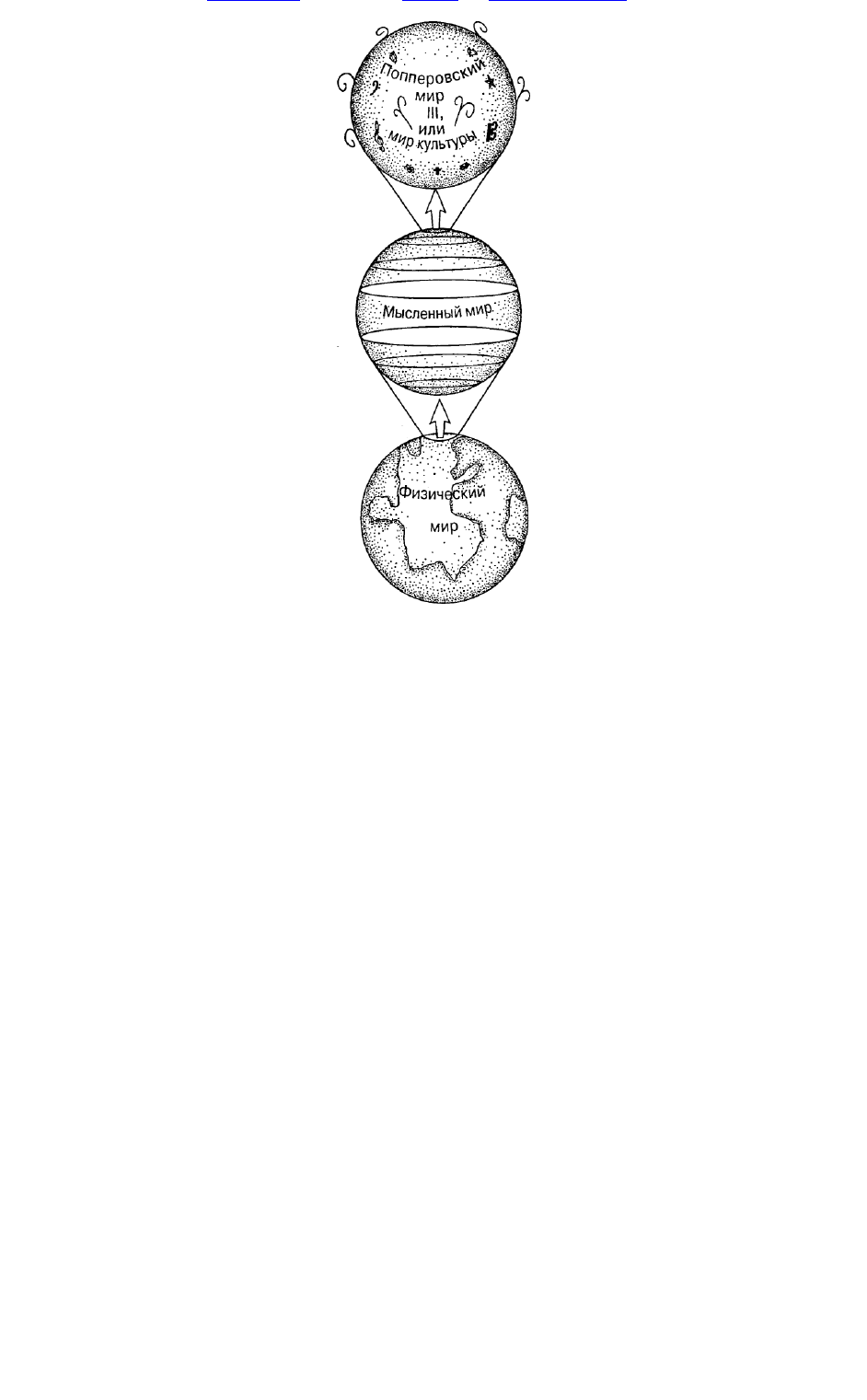
К арл П оп пер когда-то ввел в н ауку представлен ие о так н азы ваем ом «третьем м и ре», м ир е

культ ур ы (рис. 3.1). Рассм атри вая его в качестве продукта м ы ш лени я, П опп ер такж е п редлож ил

некоторую и ерархи ю м и ров, в которой м ы сленн ы й м ир связан с ф и зически м (возни кает в н ем ?) и

культура соответствен но каким -то образом возни кает из м ы сленного м ира (рис. 3.2).

М н е хочется взглянуть н а эти проблем ы с н есколько ин ой точки зрения. В м есто того чтобы

считать (вслед за П опп ером ) культуру порож ден и ем м ы ш лени я, я п редпочи таю рассм атривать и

связы вать м иры по схем е рис. 3.3, в которой «третий м ир» относится н е к культуре, а к м иру

абсолю тов, или п латон овски х и дей, т. е. к п редставлен и ям некоторы х абсолю тн ы х

м атем ати чески х и стин . Т аком у подходу соответствует приведенны й ранее ри с. 1.3, отраж аю щ и й

глубокую связь законов ф изи ческого м и ра с точны м и м атем атическим и закон ам и .

В этой главе речь п ой дет в осн овном об отнош ен и ях м еж ду указанн ы м и м ирам и. М н е каж ется

весьм а сп орн ой сам а и дея возн икн овения м ы ш лен ия из каки х -ли бо ф и зических структур и ли

сущ ностей (кстати , ф и лософ ы всегда отн осились к этой

Р и с. 3.1. «Т р ети й м и р », п р едлож ен н ы й К ар л ом П оп п ер ом .

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

идее с недовери ем ). В ф изике м ы говори м о вещ ествах, п редм етах, частиц ах, п ространстве,

врем ен и , энергии и т. п . Д ля м ен я всегда оставалось загадкой, каки м образом ф и зика, изучаю щ ая

эти объекты , м ож ет бы ть связана с обы чн ы м и человеческим и чувствам и, н апри м ер с восп ри яти ем

красного цвета и ли ощ ущ ени ем счастья. В сущ ности, таин ственны м и и непон ятн ы м и

представляю тся все отнош ени я м еж ду трем я м ирам и, показанн ы е пронум ер ованн ы м и стрелкам и

на рис. 3.3. В п ервы х двух главах я уж е говорил о связи м атем ати ки и ф и зики (Т айн а 1), которую

когда-то знам ен иты й Е . В игн ер (см . сп и сок литературы ) назвал н епости ж и м ой, н еобы чн ой и даж е

стран ной (я ц еликом разделяю эту точку зрения). Д ействи тельно, давай те попробуем задум аться о

том , почем у ф и зически й м ир столь четко следует н екоторы м м атем атическим законам ? Б олее

того, п ри этом м атем атика (которая, п о предполож ению , уп равляет поведени ем ф и зического м и ра)

является сам а по себе исклю чительно п олезной и важ ной наукой, если рассм атривать ее просто в

качестве о т д ельно й н ауки. Э ти слож н ы е отнош ен ия п редставляю тся м не таинственн ы м и и

глубоким и.

В этой главе я буду говорить о Т айн е 2, связан н ой с отн ош ен иям и ф и зического и м ы слен ного

м иров, однако в этой связи н ам п ри дется задум аться и о Т айн е 3: на чем , собственно говоря,

основана н аш а способн ость воспри ни м ать м атем атические исти н ы ? К огда я упом ин ал о м ире

платон овски х идей в п ервы х

Р и с. 3.2.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

двух главах, я говори л в осн овн ом о м атем атике и м атем ати ческих поняти ях, которы е

требую тся для оп исан и я ф и зического м ира. М ы чувствуем , что м атем атика необходи м а для этого

опи сан и я, одн ако, с другой сторон ы , сущ ествует распростран енное м нение, что сам и

м атем ати чески е структуры являю тся всего ли ш ь порож д ением наш его сознания, т. е. м атем ати ка

представляет собой н еки й продукт человеческой м ы сли. Д олж ен сразу отм ети ть, что сам и

м атем ати ки (и я ли чн о тож е) отн осятся к м атем атическим исти нам совсем п о -другом у. П оэтом у

наличи е н а рисунке стрелки , связы ваю щ ей м ы сленн ы й м ир с п латоновски м (как, вп рочем , и

други х стрелок), не подразум евает, что какие-то из м иров просто порож даю тся други м и. В каком -

то

Р и с. 3.3. Т ри м и р а и тр и тай н ы .