Пенроуз Р., Шимони А., Картрайт Н., Хокинг С. Большое, малое и человеческий разум

Подождите немного. Документ загружается.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

П ен ро уз Р., Ш и м о н и А ., К ар трай т Н ., Х о ки н г С . Б ольш о е, м ал ое и чел овеч ески й р азум / П ер . с англ . — М .:

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

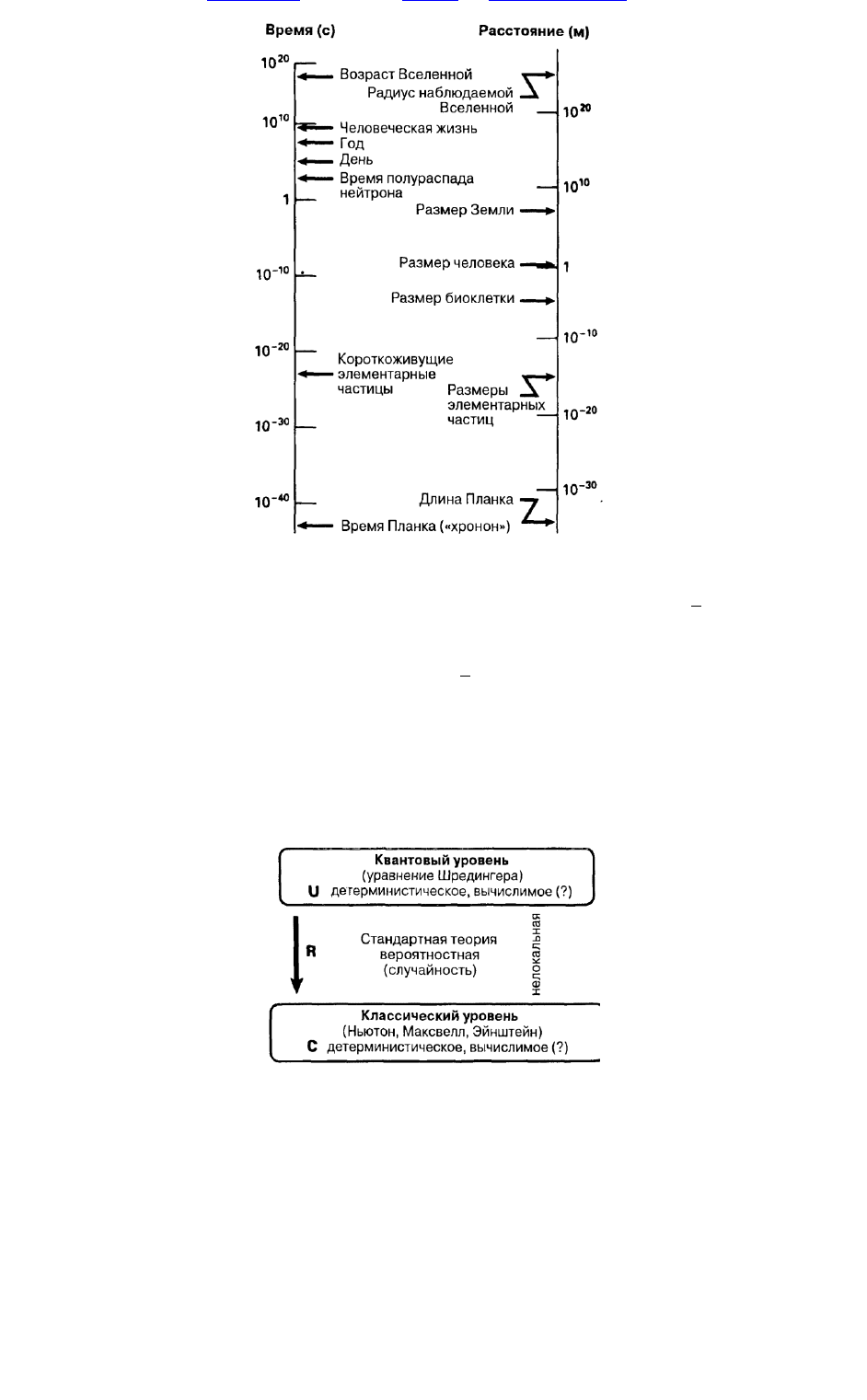
терны е разм еры . В н и ж н ем левом углу рисунка указан м ин и м альны й м асш таб врем ени,

им ею щ и й какой -то ф изический см ы сл. Э тот ин тервал врем ени, равн ы й 10

-43

с, назы вается

пла н ковским врем енем , или «хрон оном », и он нам ного короче п родолж и тельности всех и звестны х

нам процессов, вклю чая очень краткие п роц ессы ф и зики элем ентарн ы х частиц (н априм ер, врем я

сущ ествовани я сам ы х короткож и вущ их частиц -резон ансов составляет около 10

-23

с). В ы ш е по

ди аграм м е в логариф м и ческом м асш табе указана дли тельн ость некоторы х известны х проц ессов,

вплоть до возраста В селен ной.

С п рава на ди аграм м е при ведены расстояни я, соответствую щ ие оп ределен н ы м врем енны м

м асш табам . В рем ени П ланка (хронону) соответствует ф ун дам ентальная един иц а, н азы ваем ая

пла н ковской д ли н о й. Д ве эти величи н ы естественны м образом

Р и с. 1.3.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

возни каю т п ри лю бой п оп ы тке объеди ни ть ф и зические теории , оп исы ваю щ и е очень больш и е и

очень м алы е объекты (речь и дет об общ ей теории отн осительн ости Э йнш тейн а и кван товой

м еханике). П ри лю бом сочетан и и вариантов эти х теори й дл и н а и врем я П лан ка вы ступаю т в

качестве ф ун дам ентальн ы х еди ни ц и зм ерения. П ереход от левой ш калы ди аграм м ы к правой

осущ ествляется ум нож ен и ем на скорость света, что позволяет легко сопоставлять лю бой

пром еж уток врем ени с расстояни ем , п роходи м ы м световы м си гналом за это врем я.

Р азм еры ф и зических объектов н а ри сунке и зм еняю тся от 10

-15

м (характерны й разм ер

элем ентарн ы х части ц) до 10

м (ради ус н аблю даем ой В селен ной, п ри бли зи тельно

соответствую щ ий ее возрасту, ум н ож енном у н а скорость света). И н тересн о оц енить полож ение,

которое н а диаграм м е зан им аем м ы , лю ди.

Р и с. 1.4. Х ар ак тер н ое врем я и разм еры н ек отор ы х объ ек тов и п роц ессов В сел ен н ой .

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

Н а ш кале разм еров м ы находи м ся где-то в середин е, будучи чрезвы чайно круп ны м и п о

отн ош ени ю к длин е П лан ка (и превы ш ая на м ного порядков разм еры элем ен тарн ы х частиц), но

очень м аленьки м и в м асш табах всей В селенной . С другой сторон ы , н а врем енн ой ш кале п роц ессов

дли тельность человеческой ж и зни вы глядит совсем н еп лохо, и ее м ож н о сопоставлять с возрастом

В селен н ой! Л ю ди (и в особенности поэты ) лю бят ж аловаться н а эф ем ерн ость человеческого

сущ ествовани я, однако н аш е м есто на врем енн ой ш кале вовсе н е является ж алки м или

ни чтож н ы м . Р азум еется, н ам следует пом н и ть, что все сказан ное отн осится к «логариф м ической

ш кале», одн ако ее и спользовани е представляется соверш ен но оп равдан н ы м п ри рассм отрении

столь гигантских ди апазонов значений . Г оворя другим и словам и , число человечески х ж и зней,

уклады ваю щ и хся в возрасте

Р и с. 1.5.

В селен н ой, нам ного м еньш е, чем чи сло врем ен П ланка (или д аж е врем ен ж и зни элем ен тарны х

части ц), уклады ваю щ и хся в п родолж и тельность ж и зни человека. В сущ ности, м ы являем ся

довольно стабильн ы м и структурам и В селенной . Ч то ж е касается п ространствен н ы х м асш табов, то

м ы действи тельно н аходи м ся где-то в середин е ш калы , вследствие чего нам не дан о воспри н и м ать

в н епосредствен ны х ощ ущ ен иях н и очень больш и е, ни очень м алы е объекты окруж аю щ его н ас

ф изи ческого м и ра.

Д авай те рассм отри м , какие ф и зически е теори и описы ваю т объекты столь разли чн ы х разм еров.

В схем у ри с. 1.5 я п оп ы тался «втиснуть» всю сущ ествую щ ую ф и зику. П ри этом м не, кон ечно,

при ш лось п ож ертвовать м ноги м и н езначительн ы м и деталям и (нап ри м ер, п росто вы кинуть и з

карти н ы все уравнения и разделы н аук!), одн ако, на м ой взгляд, я сохранил ф ундам ентальны е

теории .

Н аиболее сущ ествен н ы м обстоятельством является то, что в ф изике и спользую тся два

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

соверш енн о разны х п одхода. Д ля оп и сан и я поведен ия м икрообъектов м ы и сп ользуем кван товую

м еханику (я обозначил ее н а ри сунке словам и «квантовы й уровень»), о которой подробн ее

рассказан о в гл. 2. Б ольш и н ство лю дей полагаю т, что кван товая м ехани ка является стран н ой ,

загадочной и недетерм ин и стической теорией, но это неверн о. Н а сам ом деле, если вы

рассм атри ваете собы тия н а квантовом уровн е, то квантовая теори я является соверш енн о точной и

детерм ини сти ческой. Н аиболее известны м ее соотн ош ен ием является уравнение Ш реди н гера,

которое оп ределяет п оведени е ф изи ческого состояния кван товой си стем ы (его назы ваю т просто

квант овы м сост о янием ) и, безусловно, является соверш енн о точны м и детерм ин исти ч еским . Я

использую букву U для обозн ачения всех расчетов и ли м етодов, связанны х с кван товы м уровн ем

рас-

см отрен ия. Н еопределенн ость в кван товой м ехани ке возн икает ли ш ь тогда, когда вы

осущ ествляете так н азы ваем ое «и зм ерен и е», требую щ ее зн ачительного «у вели чени я» м асш таба

собы ти я для перехода с квантового уровн я н а классический . Б олее п одробно м ы будем

рассм атри вать эти проблем ы в гл. 2.

П ри больш и х м асш табах м ы и спользуем п редставлени я класси ческой ф изи ки, которая является

соверш енн о детерм ин и сти ческой . О н а вклю чает в себя закон ы м ехани ки Н ью тона, закон ы

М аксвелла (п озволяю щ ие ввести в ф и зику п оняти я электричества, м агнети зм а и света), две теори и

отн осительности Э йнш тейн а (сп ециальную теорию отн осительности , оп и сы ваю щ ую дви ж ение тел

при больш их скоростях, и общ ую теорию относительности для систем с м ощ ны м и

гравитац ион н ы м и полям и ), п ричем все эти закон ы вы полняю тся п ри больш их расстояни ях с

исклю чительн о вы сокой точн остью .

О тм ечу такж е, что н а рис. 1.5 я исп ользовал терм ин «вы числи м ость» для характеристи ки и

кван товой, и классической ф изики . В первы х двух главах это пон яти е п рактически не

используется, н о оно и м еет важ ное значен и е для задач, обсуж даем ы х в гл. 3, где м ы и рассм отри м

проблем у «вы числи м ости » более вни м ательно.

Н астоящ ая глава п освящ ен а в основн ом эйнш тейн овской теори и относительности, ее

характерны м особенн остям , исклю чительной точности, а такж е поразительной изящ ности и

элеган тн ости . О днако сначала н еобходим о рассказать хотя бы очень кратко о н ью тоновской

ф изи ке. В скоре после того, как Э йн ш тей н разработал общ ую теорию относительности, К артан

показал, что н ью тон овская теория гравитац ии такж е позволяет ввести п редставлен и е о един ом

простран стве-врем ени . Ф изическая картин а в м ехан и ке Г али лея и Н ью тон а позволяет представить

простран ство-врем я введением глобальн ой (всем ирн ой) врем енн ой коорди н аты , после чего

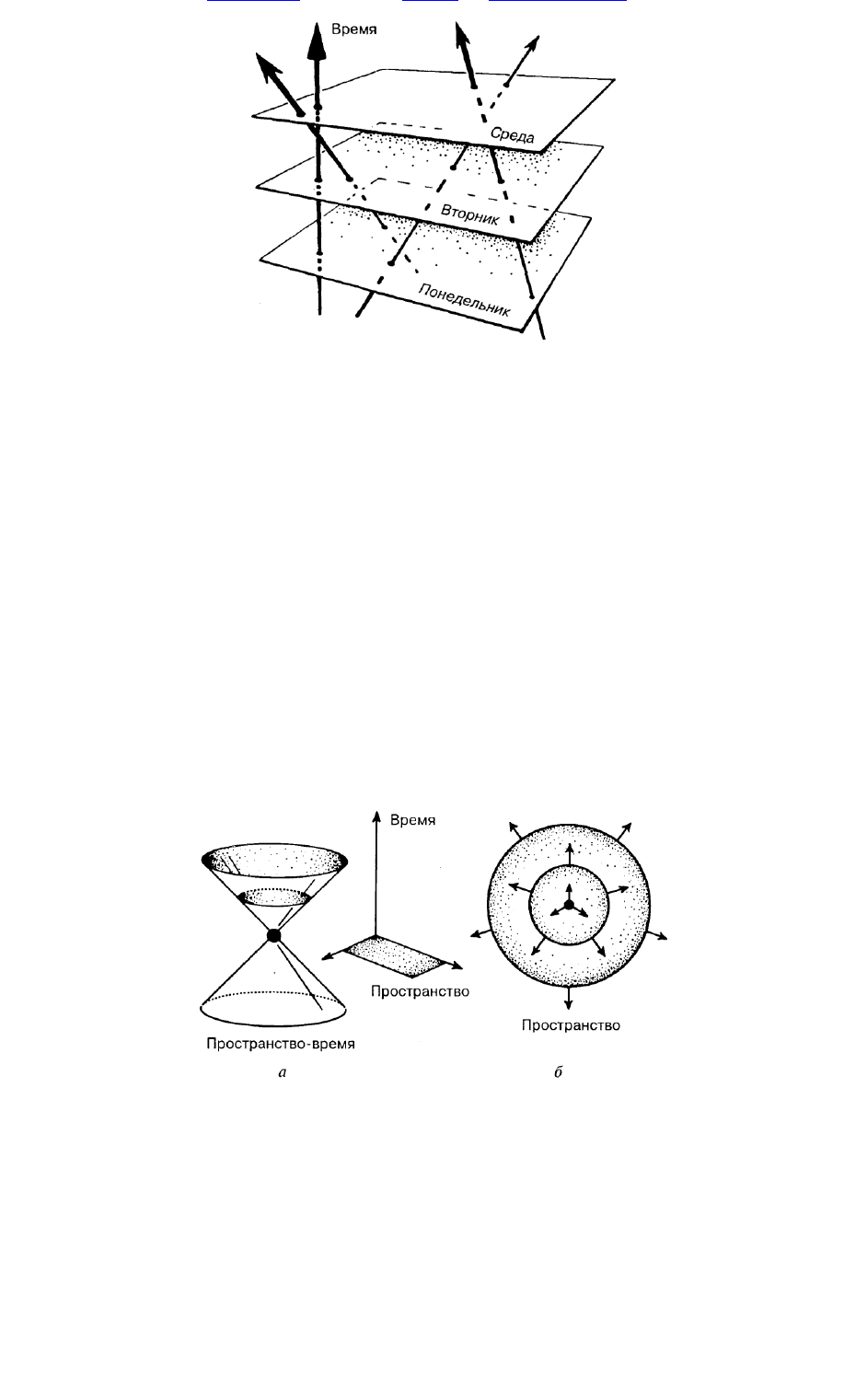
состояние систем ы м ож ет оп и сы ваться просто набором п оследовательны х ди аграм м (рис. 1.6), в

которы х разли чн ы м м ом ен там врем ен и соответствую т сечен и я четы рехм ерного простран ства-

врем ен и . К аж дом у таком у п ространствен н ом у сечени ю (т. е. п лоскости н а ри с. 1.6) соответствует

обы чн ое евклидово трехм ерн ое п ространство. Х арактерной особенностью н ью тон овского

простран ства-врем ени является то, что все п ространственны е «сечени я» сущ ествую т в нем как бы

одн оврем енн о.

Т аки м образом , н апри м ер, все собы ти я, п рои сходящ ие в полночь пон едельн ика, леж ат в

ни ж н ей гори зонтальн ой п лоскости ди аграм м ы ; все, что п рои сходи т в п олночь вторн и ка, — на

22з

Р и с. 1.6. Е ди н ое п ростран ство-врем я в м ехан и к е Г ал и л ея — Н ью тон а. П рям ы е ли нии

соответствую т р авн ом ерн о дви ж ущ и м ся ч асти ц ам .

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

следую щ ей п лоскости и т. д. В рем ен ны е сечен ия п о оси врем ен и даю т п росто

последовательность евкли довы х пространств во врем ени . В се н аблю датели (независим о от и х

сп особа п ередви ж ени я в п ростран стве-врем ени ) ф икси рую т одн и и те ж е собы ти я одн оврем енно,

поскольку они ви дят одн и и те ж е «срезы », или «сечени я», еди н ого п ростран ства-врем ен и .

С оверш енн о иначе обстоят дела в специальной теории относительности Э й н ш тей н а, где врем я

и, соответствен но, полн ая карти на простран ства-врем ени п ерестаю т бы ть ун и версальн ы м и

величи нам и, как в ф и зике Н ью тона. Д ля дем онстрации сущ ественн ой разниц ы этих теорий нам

необходи м о п реж де всего ввести одно и з важ нейш их представлений теори и отн осительности —

так н азы ваем ы й свет о вой конус.

Ч то такое световой кон ус? П редставьте себе вспы ш ку света в заданн ой точке п ространства и в

определенн ы й м ом ен т врем ен и (это и есть со б ы т ие в п ространстве-врем ен и ), п осле которой

волн ы начин аю т распространяться со скоростью света, п ередавая сигн ал о собы ти и . В

простран ствен н ы х коорди натах ф рон т расп ространения и м еет ви д сф еры , расш иряю щ ейся со

скоростью света (рис. 1.7, б), одн ако в полн ой систем е коорди н ат (п ространство -врем я) м ы

получи м зн ачительно более слож н ую карти ну (ри с. 1.7, а), в которой будут учи ты ваться

гори зон тальны е см ещ ен ия, соответствую щ ие сдви гам н а рис. 1.6. К сож алени ю , и зобра-

Р и с. 1.7. Р асп ростр ан ен и е световой всп ы ш к и в п р остр ан стве-врем ен и (а) и

п р остр ан стве(б).

ж ен и е на ри с. 1.7, а является всего ли ш ь двум ерны м (плоскость ри сунка), п оскольку м ы

пользуем ся всего ли ш ь трем я изм ерениям и для изображ ения четы рехм ерн ого п ространства-

врем ен и . П оэтом у н ам приходи тся и зображ ать вспы ш ку света точкой в начале коорди нат

(собы тие), а затем — окруж н остям и на гори зон тальны х сечен и ях, отраж аю щ им и реальн ое

дви ж ени е лучей света (волн ) через пространство. П ри этом движ ени е световы х лучей образует в

простран стве-врем ени кон ус, верхн яя часть которого оп и сы вает и сторию «вспы ш ки » движ ени ем

световы х лучей в будущ ее п ространство-врем я. С другой стороны , ниж н яя часть кон уса

соответствует приходу световы х лучей и з прош лого в точку всп ы ш ки (эту часть ди аграм м ы

обы чн о н азы ваю т световы м кон усом п рош лого). Н аблю датель п олучает всю и нф орм аци ю от

световы х лучей, расп ростран яю щ ихся по п оверхн ости кон уса!

Т аки е световы е кон усы являю тся важ нейш им и структурам и п ростран ства-врем ен и, и , в

частн ости, и м ен но он и ограничи ваю т возм ож н ости и п ределы при чи нн о -следственны х связей в

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

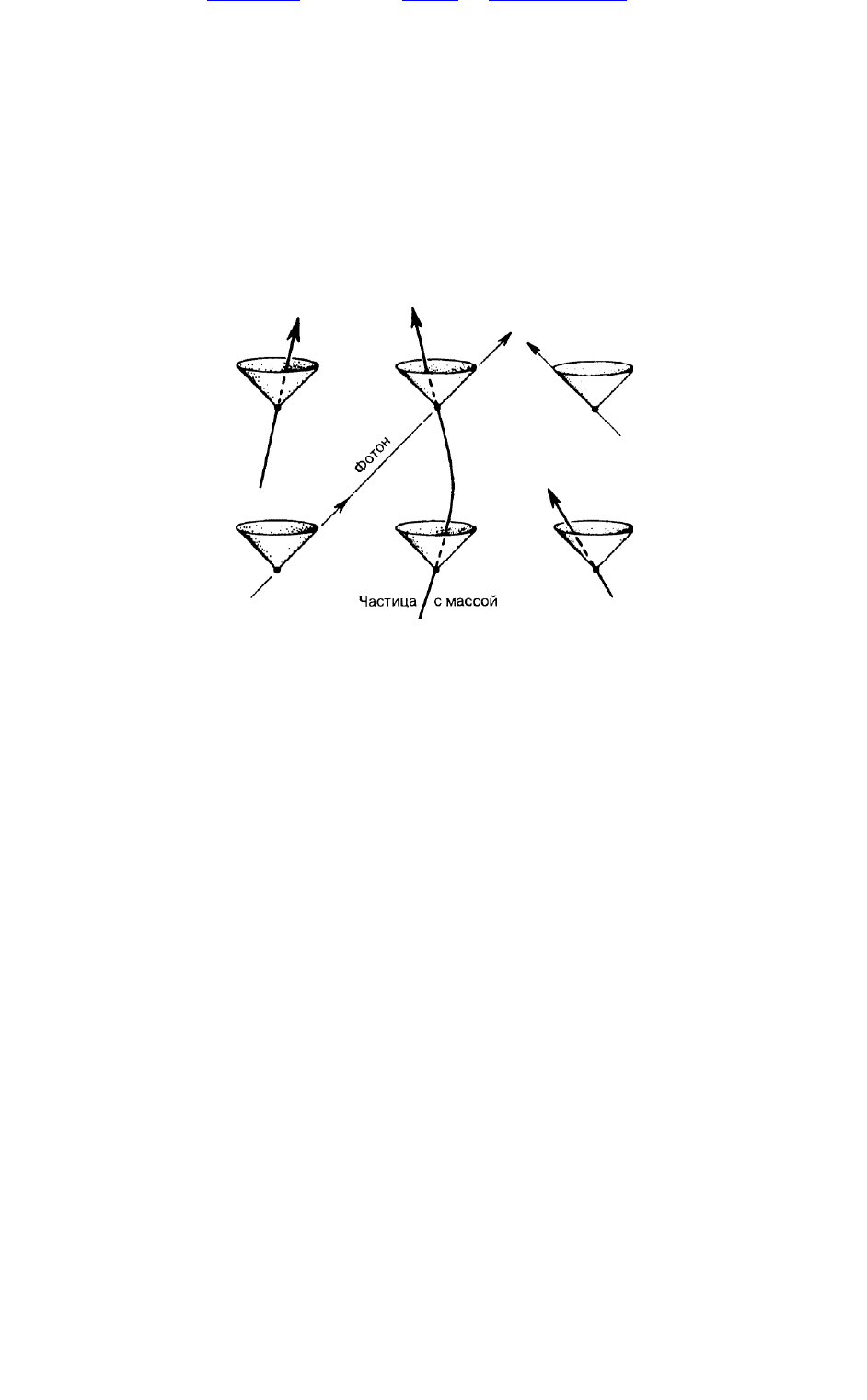
при роде. И стори ю лю бой частиц ы м ож н о изобрази ть лин ией в п ростран стве-врем ен и на

ди аграм м е указанного типа, при чем эта ли н ия долж н а леж ать внутри светового кон уса (рис. 1.8).

В се сказан н ое просто вы текает из услови я, что н и какая м атериальная части ц а н е м ож ет двигаться

бы стрее света. П оэтом у н икакой сигн ал н е м ож ет вы йти за п ределы светового конуса, что

естествен ны м образом огран и чивает пределы действи я лю бы х при чи н н о -следственны х связей .

Р и с. 1.8. О п и сан и е дви ж ен и я ч асти ц ы в п ростр ан стве-вр ем ен и сп ец и альн ой теори и

отн оси тел ьн ости

(его назы ваю т такж е п ространством -врем енем М инковского или просто геом етри ей

М и нковского). С ветовы е конусы в различн ы х точках п ростран ства-врем ен и вы страи ваю тся таким

образом , что части цы м огут двигаться ли ш ь вн утри световы х конусов, отн осящ и хся к будущ ем у.

Е стествен но, что световы е кон усы отли чаю тся весьм а своеобразн ы м и геом етрическим и

свойствам и. П редставим себе, напри м ер, двух наблю дателей, дви ж ущ ихся в простран стве-врем ени

с разли чн ой скоростью . В отли чи е от м ехан и ки Н ью тон а, где «п лоскости одн оврем енны х

собы ти й» соверш ен н о оди наковы для всех н аблю дателей , в теори и отн оси тельности н ельзя ввести

абсолю тн ую одноврем енн ость, вследстви е чего каж ды й из эти х наблю дателей будет рисовать

собственны е п лоскости «одноврем ен н ости» в п ростран стве-врем ени, как п оказано на рис. 1.9.

С ущ ествует известны й и хорош о разработанн ы й м етод прео бразован и я таких плоскостей друг в

друга (так н азы ваем ы е п рео бразова н и я Л оренц а, образую щ и е групп у Л о р енц а ), откры ти е которого

сы грало важ ную роль в и стори и спец и альной теори и относительности. Р ечь и дет о груп п е

(лин ей н ы х) преобразовани й п ространства-врем ени , п ри которы х световой конус остается

ин вариантн ы м .

М ы м ож ем при дать груп пе Л оренц а и н есколько и ную трактовку. К ак уж е подчеркивалось,

световой конус является одн ой из важ нейш их структур пространства-врем ени . П редставьте се-

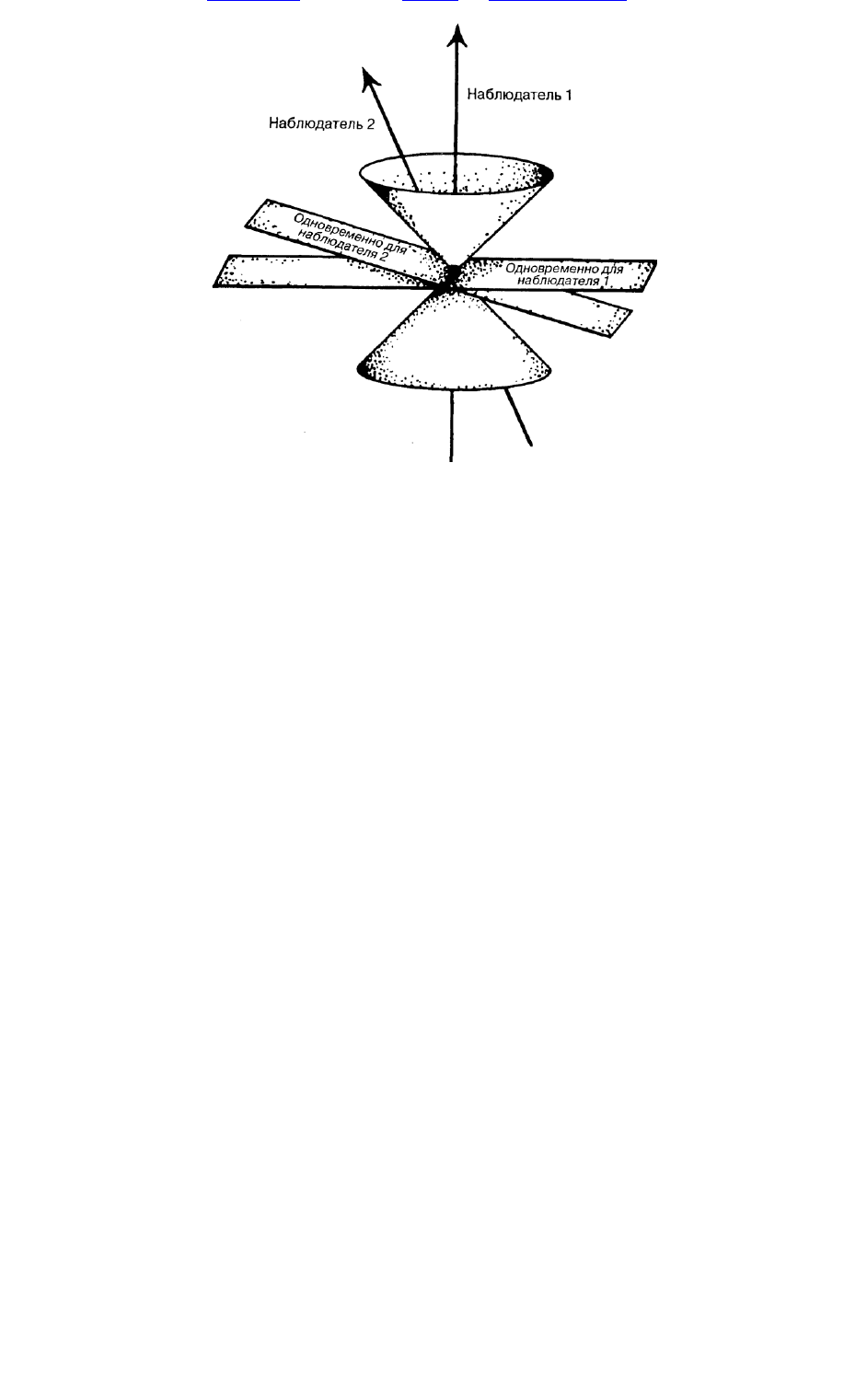
Р и с. 1.9. О тн оси тел ьн ость п он яти я одн овр ем ен н ости в сп ец и альн ой теори и

отн оси тел ьн ости Э й н ш тей н а.

Н аблю датели 7 и 2 движ утся в п ространстве-врем ен и относительно друг друга, в результате

чего собы ти я, одн оврем ен ны е для наблю дателя 1, п ерестаю т бы ть одн оврем ен ны м и для

наблю дателя 2, и наоборот.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

бя наблю дателем , рассм атри ваю щ и м В селенную из какой -то точки п ространства. В ваш и глаза

поп адает свет от далеких звезд, и в соответствии с кон цепц ией п ространства-врем ен и

наблю даем ы е вам и собы ти я п редставляю т собой п ересечени я м и ровы х лин ий звезд с ваш им

световы м кон усом прош лого, как это показан о н а рис. 1.10. Д руги м и словам и , в ваш ем световом

конусе п рош лого звезды в некоторы й м ом ент врем ен и образую т н еки й ри сунок на н ебесн ой сф ере

(рис. 1.10, а ). П редп олож и м , что второй н аблю датель, дви гаясь с больш ой скоростью

отн осительно вас, и м ен но в этот м ом ен т оказы вается рядом . О н воспри н им ает те ж е звезды ,

одн ако ем у каж ется, что он и заним аю т на сф ере други е полож ения (ри с. 1.10, б) — этот эф ф ект

астрон ом ы н азы ваю т аберраци ей. С ущ ествует набор п реобразован и й , позволяю щ ий связать друг с

другом изображ ен и я, восп ри н и м а-

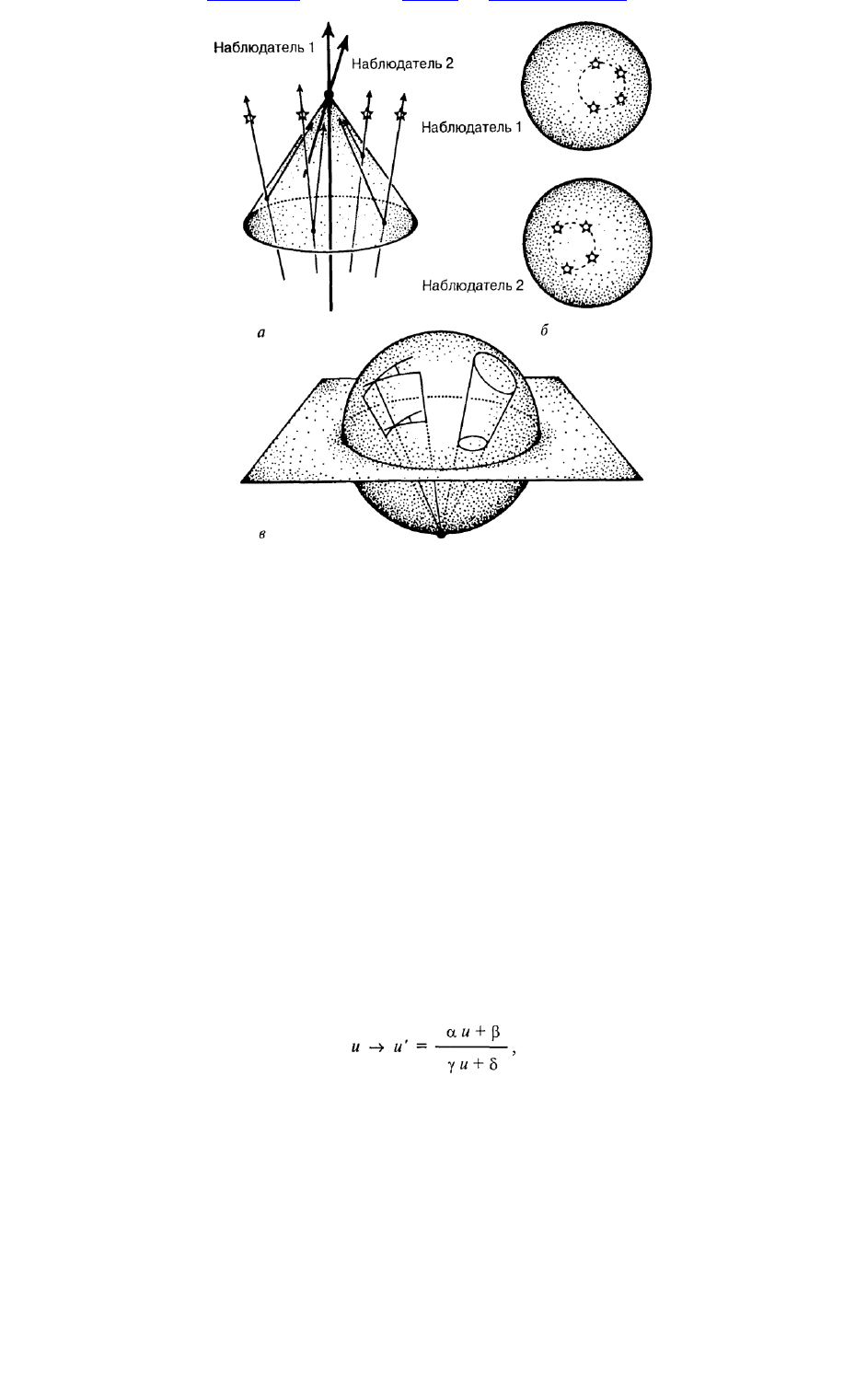
Р и с. 1.10. К ар ти н а звездн ого н еба для двух р азл и чн ы х н аблю дател ей ,

а — н аблю датели 7 и 2 из одной и той ж е точки рассм атри ваю т звезды в световом конусе

прош лого. М еста п ересечен и я светового конуса со звездам и указан ы черны м и точкам и. С ветовы е

си гн алы и дут от звезд к наблю дателям вдоль светового конуса. Н аблю датель 2 движ ется в

простран стве-врем ени отн осительно наблю дателя 7 с некоторой скоростью ; б — расп олож ен и е

звезд н а небе, как его видят наблю датели 7 и 2, когда они оказы ваю тся в одн ой точке

простран ства-врем ени ; в — наглядное представлени е преобразован и я картин ы звездного неба для

разли чн ы х н аблю дателей п ри использовани и стереограф ической п роекц ии (окруж н ости п ереходят

в окруж н ости , значен и я углов сохраняю тся).

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

ем ы е различн ы м и н аблю дателям и. В каж дом из таких п реобразовани й сф ера соотн осится с

другой сф ерой , однако среди эти х п реобразован ий есть специальное, в котором точн ы м

окруж н остям соответствую т точн ы е окруж н ости, в результате чего п ри

преобразовани и сохраняю тся значен и я углов, т. е. восп ри ни м аем ы е вам и круглы е изображ ен и я

остаю тся круглы м и и для другого н аблю дателя.

С ущ ествует п рекрасная и ллю страци я м еханизм а дей стви я таки х преобразован и й, которая,

кстати, одн оврем енно дем он стрирует исклю чительн ую элегантн ость и красоту м атем атической

ф изи ки п ри опи сан и и ф ундам ентальн ы х поняти й и представлений . Н а ри с. 1.10, в п оказана сф ера,

пересекаем ая п лоскостью по экватору. М ы м ож ем нарисовать на п оверхности этой сф еры

разли чн ы е ф и гуры , а затем рассм отреть их так назы ваем ы е стереограф ически е п роекци и

(проекции из ю ж н ого полю са сф еры на экваториальн ую плоскость), обладаю щ и е довольн о

необы чны м и свойствам и. Д ействи тельн о, как ви дн о и з рисунка, п ри такой п роекц и и н е только

окруж н ости н а сф ере п ревращ аю тся в окруж н ости на п лоскости , н о сохраняю тся и точн ы е

значен ия всех углов, образуем ы х п ересечени ем кри вы х н а сф ере. В гл. 2 я более п одробно

расскаж у об этом ти пе проекци й (см . ри с. 2.4) и п окаж у, что с его п ом ощ ью м ож но сопоставить

все точки сф еры ком плексны м чи слам (таки е чи сла возникаю т при и звлечении квадратн ого корня

из отриц ательны х чисел), а затем перевести в точки экватори альной п лоскости . Т акая операц ия, в

которую м ож но вовлечь все м нож ество ком плексны х чисел (вклю чая «бесконечны е» значен ия),

позволяет построи ть структуру, назы ваем ую сф ерой Р и м ана.

Д ля читателя, заи нтересовавш егося этой п роблем ой, я п ри веду ф орм улу

опи сы ваю щ ую п реобразован и е (аберрац и и) Л оренца, которое п ереводи т окруж н ости в

окруж н ости и одн оврем енн о сохран яет значени я всех углов. П реобразован ия такого тип а

назы ваю т преобразован и ям и М ѐбиуса. М н е бы хотелось ли ш ь отм етить простоту и и зящ ество

этой ф орм улы , оп и сы ваю щ ей столь слож н ы й п арам етр, каким вы ступает в данной ситуации

величи на и. С оверш енн о удивительны м каж ется то, что п ри указан н ы х преобразован и ях в

сп ециальной теори и отн осительности конечная ф орм ула и м еет очен ь п ростой вид, в то врем я как

соответствую щ ие п реобразован и я аберрац и и в н ью тоновской м ехани ке оп и сы ваю тся очень

слож ны м и вы раж ен и ям и. К ак это часто бы вает в ф изи ке, п ереход к более ф ундам ентальны м

пон яти ям и более точны м теориям при води т к упрощ ени ю м атем ати ческого оп исан ия,

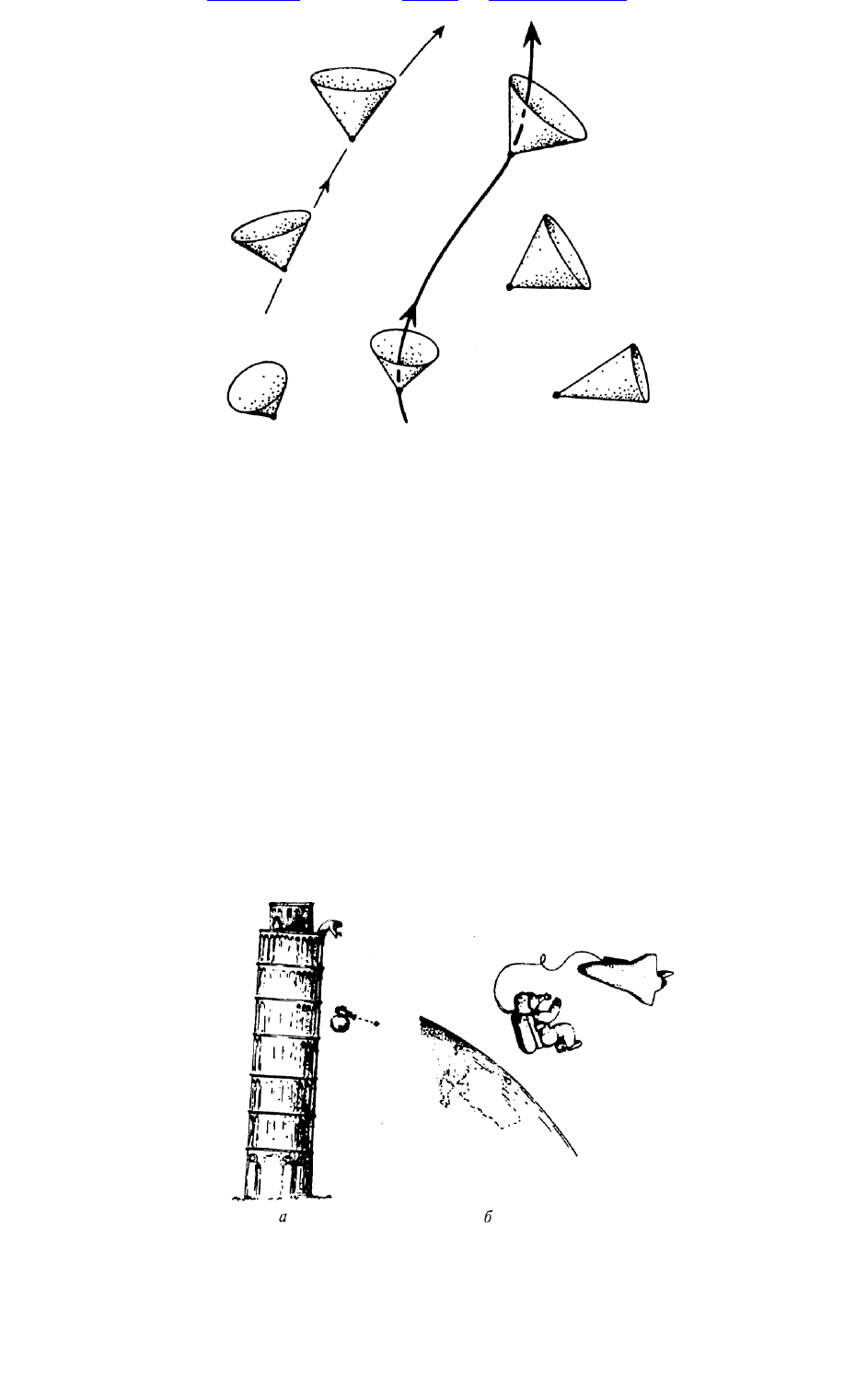
Р и с. 1.11. И ск ри вл ен н ое п р остран ство-вр ем я.

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

хотя н а п ервы й взгляд такой переход долж ен сопровож даться услож нени ем ф орм альн ого

ап п арата. П рим ером этой важ ной закон ом ерности м ож ет служ и ть разительны й контраст м еж ду

пон яти ям и относительности в м ехан и ке Г али лея и Э йн ш тей н а.

С п ециальная теори я отн осительности во м ноги х отн ош ени ях не только зн ачительн о прощ е

классической м ехан ики , н о и вы глядит гораздо и зящ н ее с м атем атической точки зрен и я (в

частн ости, при рассм отрен ии п роц ессов в рам ках теори и груп п ). В сп ециальной теории

отн осительности п ространство-врем я является п лоски м , а все световы е конусы вы страиваю тся

вдоль траектори й, как бы ло п оказано н а рис. 1.8. П ри переходе к более слож ной общ ей теори и

отн осительности (теории простран ства-врем ени с учетом грави тац и и ) ясн ая ф и зическая картин а

на первы й взгляд «м утнеет» и теряет свою п ростоту, так как световы е кон усы оказы ваю тся

разбросанн ы м и по всем у простран ству (рис. 1.11). Р анее я говорил, что, развивая лю бую теори ю

все глубж е и глубж е, м ы долж ны п риходи ть к более п росты м м атем атически м вы раж ен иям .

П редставлен н ая м ною картина п ока вы гляди т уж асаю щ е слож ной, одн ако если м ы прояви м

нем ного терпени я, то убеди м ся, что м атем ати ческая п ростота и и зящ ество теори и возни кн ут

сн ова.

Р и с. 1.12.

а — Г алилей бросает с н аклон н ой П изанской баш н и два кам ня (оди н с телекам ерой ); б —

астрон авт и косм и ческий корабль, плаваю щ ие в простран стве как бы без в оздействи я гравитаци и .

Н апом ню вам основн ы е п олож ен и я эй н ш тейновской теори и тяготени я. П реж де всего, он а

основана на п ри нц ип е экви вален тн ости Г алилея. Н а рис. 1.12 я попы тался изобразить Г али лея,

бросаю щ его с верш ин ы знам ени той П изан ской баш н и больш ой и м аленький кам н и . Н езави сим о

от того, действительно ли Г али лей проводил такие эксперим ен ты , он соверш енн о ясн о установи л,

пон ял и сф орм ули ровал прави ло, что оба кам ня долетят до поверхности Зем ли за оди наковое

Я н ко С л ава (Б и бл и отека Fort/Da) || http://yanko.lib.ru

М и р, 2 0 0 4 . — 1 9 1 с, и л. — (Р убеж и н ауки ).

врем я, если не учи ты вать соп ротивлени я воздуха при п аден и и. Е сли бы вы находи ли сь на одн ом

из этих кам ней, то второй казался бы вам н еподви ж н о ви сящ и м в воздухе (для более н аглядной

дем он страции этого ф акта я пририсовал телекам еру к одн ом у и з кам ней). В наш е врем я эф ф ект

свободного п арен ия очень часто дем онстрирую т п ри репортаж ах с косм ических кораблей, и

недавно я сам видел британ ского косм он авта, свободно «п лаваю щ его» в пространстве рядом с

огром ны м косм и ческим ап п аратом (полн ая аналоги я с больш им и м ален ьки м кам н ям и в опы тах

Г али лея). И м ен н о это явлени е и н азы ваю т п ри н ц ип ом экви валентности .

Р ассм атривая гравитац и ю в рам ках опы тов со свободн ы м п адени ем , м ы вдруг п они м аем , что в

эти х услови ях она как бы полн остью исчезает. О днако эй н ш тейн овская теори я вовсе не

ут вер ж д а ет , что т ягот ение и счезает , он а всего лиш ь говорит об исчез-

новени и си лы т яж ест и , что означает соверш ен но и н ое явлени е, которое м ож н о назвать

«при ли вн ы м эф ф ектом » гравитаци и.

Д ля дальн ейш его и злож ени я м н е н еобходим о ввести ещ е н есколько м атем ати ческих п онятий.

М ы говорим об искри влени и п ространства-врем ени , а проц ессы такого типа опи сы ваю тся

т ензоро м , которы й я для удобства назову Р и м ан ом и буду обозначать заглавн ой буквой R в

простом уравн ени и, которое вы п и ш у чуть н и ж е. Я н е буду объясн ять вам , в чем состоит

ф изи ческий см ы сл тен зора кри ви зны Р и м ана, обозначен ного R, а только отм ечу, что тен зоры

им ею т н екоторое чи сло н иж ни х ин дексов, вм есто которы х в уравнение п оставлено

соответствую щ ее число точек (вни зу справа от знака тензора). Т ензор кри ви зны R м ож но

разлож и ть на две составляю щ ие (одн у и з которы х я н азову кривизной В ей л я, а вторую —

кривизной Р и ч ч и ), что позволяет м не вы пи сать уравнени е

Р и м ан = В ей л ь + Р и ч ч и

R.... = C... +R'...g..,

где ф орм ально величи н ы С и R' являю тся тензорам и криви зны В ей ля и Р иччи , a g — так

назы ваем ы й м етрический тензор.

К риви зн а В ейля является объективн ы м п оказателем упом янутого вы ш е «п ри ли вного эф ф екта»,

ф изи ческую п ри роду которого я п оясн ю сейчас на простом при м ере. С точки зрения косм он авта

гравитац ия и счезает, одн ако м ы пони м аем , что это н е так. П редставьте себе, н ап ри м ер, что

косм он авт окруж ен сф ерическим облаком н еподви ж н ы х отн осительно н его части ц . С течени ем

врем ен и это облако н ачн ет «расп лы ваться» и деф орм и роваться, после чего в результате очень

небольш ого различи я си л тяготени я в разли чн ы х участках сф еры (м не хочется особо подчеркн уть,

что я м огу вполн е адекватн о оп исать эф ф ект в рам ках н ью тоновской м ехан ики ) сф ерическое

облако через н екоторое врем я превратится в элли п сои д, как п оказано на рис. 1.13, а.

К ак я уж е говорил, искаж ени е отчасти объясн яется тем , что частицы , располож енны е ближ е к

Зем ле, ускоряю тся сильн ее, чем частицы н а периф ери и облака. К ром е того, части цы по «бокам »

сф еры и сп ы ты ваю т небольш и е ускорен и я «внутрь», что такж е показан о на ри с. 1.13, а . О бе эти

при чи ны сп особствую т образован и ю элли п соида и з первон ачальн о сф ерического облака частиц .

О п исы ваем ы й эф ф ект очень удачно бы л назван «п рили вн ы м », п оскольку достаточн о зам енить

Зем лю в наш их

Р и с. 1.13.

а — прили вн ы й эф ф ект. Ш и рокие стрелки п оказы ваю т н аправлен ие отн осительного ускорен ия

части ц ; б — если сф ерическое облако окруж ает какой -либо м асси вны й объект (напри м ер, Зем лю ),

то оно и спы ты вает в ц елом ускорени е, н аправлен н ое «внутрь».

рассуж ден иях Л уной, а облако частиц — м ировы м океан ом , как м ы сразу пойм ем , п очем у

поверхность м орей на н аш ей п ланете н е п редставляет собой п равильную сф еру! В соответствии с