Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

432 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

ductile fracture after initial signiﬁcant plastic deformation. At the same time,

b. c. c. metals show brittle fracture at low temperatures.

In the case of silver [31], the material fracture occurs in creep mechanism

at low tensile stresses (σ/E < 10

−3

). Nucleation of voids and boundary sliding

take place in intergranular fracture. Transgranular fracture is accompanied by

the void nucleation at inclusions and the void growth together with the creep

strain. The strain localizes in weaken cross-section of the sample that leads to

growth of local stresses and rupture. High stresses cause ductile fracture also

with the void nucleation at inclusions. At increasing of the stresses, fracture

occurs in the mechanism, which is proper for polycrystals, when nucleation

and growth of cracks and voids at the grain boundaries are facilitated. Finally,

the fracture occurs in dynamical regime with propagation of stress waves in

the sample bulk.

In the case of molybdenum [301], three regions of brittle fracture by cleav-

age are added in the fracture chart, namely (i) on the nucleus cracks, prelim-

inary existing in crystal; (II) on the nucleus cracks, forming at coalescence

of dislocations in initial stage of plastic strain (microplasticity), and (III) the

plastic strain attains a signiﬁcant level (∼10%), but the fracture takes place

owing to the cleavage. Similar fracture charts for high-temperature supercon-

ductors can signiﬁcantly help in design and processing of HTSC JJs with

optimum characteristics. Finally, note [487, 1152] as successful examples of

development of the system analysis methods, including creation of the ma-

terial property charts, used for estimation of critical behavior of the HTSC

materials and composites.

9.8 Concluding Remarks

The results for diﬀerent toughening mechanisms, actually acting in HTSC

microstructures, and also the features of the fracture resistance alterations

due to the growth of crack-like defects have been presented in Chaps.8 and

9. They have conﬁrmed an existence of the numerous and non-simple eﬀects.

At the same time, today in the applied superconductivity, the simpliﬁed ap-

proaches to estimation of the strength and fracture toughness are widespread.

For example, the following relation is widely applied [198, 614, 911, etc.]:

= YK

1/2

, (9.34)

where σ

is the fracture stress, Y is a geometric constant, K

is the fracture

toughness and c is the ﬂaw size.

However, it is well known (see, e.g. [157, 262, 423, etc.]) that (9.34) has

been stated in the framework of the classical Griﬃth-Irwin’s approach [348,

473] for homogeneous linear-elastic solid under homogeneous loading.This

equation could be applied only under conditions of real dominating crack

with size considerably greater than microstructure scale and in the absence of

9.8 Concluding Remarks 433

internal (residual) stresses. Obviously, an account of these macrocracks is no

interesting for HTSC, because the superconducting and transport properties

very rapidly degrade even in an insigniﬁcant microcracking. Moreover, as has

been shown above, the HTSC microstructure is very heterogeneous with het-

erogeneity scale, being compared with characteristic microcrack size. Finally,

the HTSC compositions undergo non-homogeneous loading during working

and possess considerable residual stresses, initiated by processing. Note also

that another fracture mechanisms act by small fracture stresses. Hence, the

use of (9.34) could lead to incorrect conclusions, for example, “K

can be im-

proved [in REBCO] by the reﬁnement of the RE-211 particle size” (see [911],

p. 111), or “K

is independent of ﬂaws in the material (cracks, pores...) and,

therefore represents a true property of the Y-123/Y-211 compound” (see [614],

p. 2074). Violation of the dependence between σ

and K

, given by (9.34), is

evident, for example, from Fig. 8.15. Obviously, (9.34) could be applied only

in the absence of acting toughening and crack ampliﬁcation mechanisms and

under conditions of other restrictions described above.

The coming certiﬁcation of HTSC systems will demand correct deﬁnition

of the strength properties. The combination of the above considered toughen-

ing and crack ampliﬁcation mechanisms could exert on fracture resistance not

only summary eﬀect but also multiplication eﬀect. Therefore, for every actual

toughening (or crack ampliﬁcation) mechanism, ratio K

or G

should

be deﬁned, where K

) is the critical SIF (critical strain energy release rate)

due to actual toughening (or crack ampliﬁcation) mechanism and K

)is

the corresponding intrinsic parameter without toughening (or crack ampliﬁ-

cation). Then the total fracture resistance (in the force and energy approach,

respectively) should be found as

tot

i=1

(i)

; (9.35a)

tot

i=1

(i)

, (9.35b)

where n is the common number of the toughening and crack ampliﬁcation

mechanisms.

The research of eﬀectiveness of the HTSC toughening mechanisms should

be accompanied by the study of the HTSC conductivity because it is often

these eﬀects which are contrary to each other (see, e.g, [577, 822]). The mod-

eling of the current-carrying properties of HTSC system is the main aim of

the ﬁnal chapter of the monograph.

Modeling of Electromagnetic

and Superconducting Properties of HTSC

10.1 Modeling of Intercrystalline Dislocations

There are two basic approaches for description of intercrystalline structures

[43], namely (i) the structural unit approach, focuses on the atomic arrange-

ment at the intergranular boundary and (ii) the intergranular boundary dis-

location (IBD) approach, based on the periodic strain ﬁeld that is observed

at many intergranular boundaries. Both models use a coincidence site lat-

tice (CSL) description of the intergranular boundary geometry. While these

models are equivalent [48], each one has its own advantages in description

of the intercrystalline structure. Nevertheless, today studies of intergranular

boundaries in HTSCs focus primarily on the IBD description.

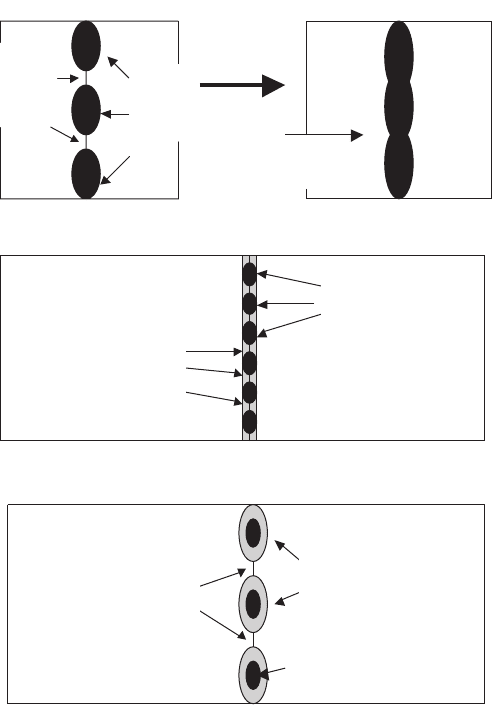
The structure of intergranular boundary may be presented, consisting of

two diﬀerent types of parallel conducting channels, disposed along the bound-

ary and deﬁned by dislocation structure (see Fig. 10.1). One of them possesses

approximate structure and properties of superconducting crystal, associated

with the regions between dislocations. Other channel is normal one or demon-

strating a weak superconductivity, and it is compared with dislocation cores

or their elastic deformations [406]. When the misorientation angle, θ,increases

then the dislocation density increases, the interdislocation spacing diminishes

which leads to gradual inhibition of the superconducting channels and to forc-

ing of the weak link behavior. Therefore, an understanding of IBD nature is

very important for statement of transition from the strong link behavior to

the weak one.

The IBD models are based on the concept that the grain boundary free

energy is particularly low for a certain set of special misorientation relation-

ships, θ [hkl]. In this case, the boundaries with θ [hkl] values other than special

ones relax into a conﬁguration in which sites of a low-energy structure are pre-

served by a localized rotation of the crystals. The macroscopic θ [hkl]andits

deviation from a low-energy misorientation are produced by the introduction

of a regular array of dislocations that rotates one crystal relative to the other

on a macroscopic scale. On the microscopic scale, these dislocations separate

436 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

(a)

(b)

Strong

Supercon-

ducting

Channels

Normal or

Isolating

Dislocations

θ ≤ 5°–10°

θ ≥ 5°–10°

(θ ≤ 20°)

(

θ ≥ 15° – 20°)

Current-Currying

Channels with Weak

Superconducting

Links

Cores of

Normal or

Isolating

Dislocations

Regions

of Strong

Links

Strong

Superconducting

Channels

Core of Normal

or Isolating

Dislocation

(c)

Mutual Re-

covering of Cores

(Tunnel Barrier)

Fig. 10.1. Three models explaining intergranular values of J

in thin YBCO ﬁlms

with [001] direction vs intergranular boundary structure: (a) model of dislocation

cores before and after their partial recovering (Dimos model) [149, 205]; (b)model

of Dayem’s bridge [920] and (c) model of channel with strong links [280]

the sites of boundary with low-energy structure. Thus, most intergranular

boundaries are presented as being divided into regions of “good ﬁt,” having

low-energy atomic structure, separated by a net of “bad ﬁt” of IBDs. As the

diﬀerence between the actual misorientation relationship and the low-energy

one increases, the spacing of the dislocations decreases and the fraction of bad-

ﬁtting region increases. A CSL construction is used to identify the low-energy

misorientations and describe the structure periodicity of the boundary. The

IBD model suggests that low energy is associated with relatively short-period

10.1 Modeling of Intercrystalline Dislocations 437

CSLs or, equivalently, low-coincidence index, Σ (where Σ is the fraction of

lattice sites of one crystal that is coincident with the other [427]).

CSLs can form in orthorhombic and tetragonal crystals only when the

squares of the lattice parameters all form rational ratios (i.e., a

: b

: c

are

rational numbers) [547]. This condition is rarely met in real crystal structures.

The approach selected to apply the coincidence concept to these systems is

to impose a small strain on the lattice in the boundary vicinity. This strain

forces the lattice parameters to meet the rational ratios condition, and the

lattice can form CSLs. The CSLs, resulting under strained conditions often

are called constrained CSLs (CCSLs). Usually, the additional strain is at-

tributed to additional sets of dislocations that are localized in the boundary

and become part of the IBD structure. Thus, the IBD structure has two com-

ponents, one to produce the correct axial ratios and other to accommodate

deviations from low-energy misorientations. Because the strain-producing and

deviation-accommodating IBDs can have opposite signs, the dislocation den-

sity may not increase monotonously with the deviation from the exact CCSL

misorientation relationship. As a result, the minimum spacing may not exist

at the CCSL misorientation and widely spaced IBD structures may accom-

modate rather large deviations from lattice coincidence [547]. This leads to a

boundary division into seemingly diﬀerent patches.

There are at least two reasons to explore the (C)CSL/IBD model. First,

it is necessary to identify the fundamental origin of the weak-link problem

in order to discern whether one is intrinsic to the boundary structure or ex-

trinsic. The second cause is connected with identiﬁcation of certain types of

inergranular boundaries other than low-angle boundaries that have speciﬁc

properties [43].

Because the structures of boundaries that lie parallel to low-index planes

of the CCSL have the shortest wavelength periodicity possible for that misori-

entation relationship, their energies are expected to be minimum and faceting

onto those planes might be expected. In this case, the modeling of intercrys-

talline structure is simpliﬁed in strongly faceting structures, because macro-

scopic boundaries with a variety of boundary planes can be considered as

mixtures of some boundary facets, each of which has a ﬁxed structure. The

CSL and CCSL conceptions can be used to optimize intergranular boundary

behavior. At the same time, they are not the governing structures due to the

following reasons [43]:

(1) Because the unit-cell dimensions are allowed to vary to achieve coinci-

dence, relatively low-Σ misorientations densely populate θ [hkl] space. As

a result, for many observed boundary misorientation relationships there

are several nearby CCSLs that may be used to the boundary description.

(2) The types of relaxations that occur in these boundaries often assume

statement of compromise between the magnitude of the local strain, re-

quired to achieve coincidence, the achievement of low Σ values and the

minimization of strain energy due to dislocations.

438 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

(3) The choice of an appropriate CCSL is complicated by the absence of a

suitable estimation for possible deviations from the exact coincidence mis-

orientation that reasonably can be referenced back to a particular CCSL.

This criterion must state the compromise between strains, low Σ, the

mechanism by which the strain is accommodated and the possible non-

monotonic dependence of the dislocation spacing on Δθ.

The elastic strains, produced by the IBD arrays in individual facets, can be

estimated using the equations derived for isolated pure-edge dislocations in an

isotropic medium [1138] and assuming reasonability of this approximation for

elastically isotropic material in the ab-plane [1079]. Then, the net strain ﬁeld

produced by a ﬁnite array of dislocations can be calculated using the super-

position method. The numerical results obtained for a boundary containing

seven equally spaced edge dislocations show that the material volume within

about 20 nm of the facet junction can deform ∼ 0.8% or more. In comparison,

the orthorhombic to tetragonal phase transformation is accompanied by an

analogous strain ∼ 1% [1079].

Conventional model [427] describes a symmetric low-angle grain boundary

(GB) by a chain of edge dislocations with the Burgers vector perpendicu-

lar to the GB plane. However, the structure of GBs in HTSC can be more

complicated due to existence of partial dislocations and facets at GBs, long-

range strain ﬁelds and compositional variations near GBs [43, 94]. The IBD

structures inﬂuence the change of J

due to an alteration of local composition

and hole concentration, additional electron scattering and signiﬁcant strains

near the dislocation cores. The models [241, 714, 920] have been proposed,

in which the current channels in GBs are described as an array of parallel

point contacts, which demonstrate weak-link behavior if their width becomes

smaller than the superconducting coherence length ξ [630]. The theoretical

description of the rapid decreasing of J

(θ) with increasing θ is usually as-

cribed by the strain-induced compositional suppression of superconducting

order parameter near dislocation cores or in the layer of some thickness near

GBs [43, 241, 714, 920]. Due to insuﬃciency of these phenomenological mod-

els, another model is presented in [373], which describes J

(θ), taking into

account the GB dislocation structure. It is assumed that the strains and ex-

cess ion charge of the GB dislocation structure can locally induce a dielectric

phase near dislocation cores and cause progressive overall suppression of the

superconducting order parameter with θ in a narrow layer of the order of the

screening length near GBs. The model provides an intrinsic mechanism for

the rapid decreasing of J

(θ)withθ, solving the Ginzburg–Landau equation

[182, 617], which describes well the practically important temperature range

for HTSC (T>77 K).

Dislocation model [690] computes a stress state at intergranular bound-

aries of three types, namely symmetrical and anti-symmetrical tilt ones with

periodical system of edge dislocations, and also symmetrical tilt boundaries

with arbitrary system of the edge dislocations. The angle dependencies of

10.1 Modeling of Intercrystalline Dislocations 439

intercrystalline critical currents are calculated in these computations. More-

over, it is shown that adequate description of superconducting features of the

boundaries can be obtained only in the framework of the arbitrary distributed

dislocations.

The models of local increasing of the critical temperature (T

), compared

to corresponding values of the bulk critical temperature (T

) due to structure

defects, causing the long-range strains, are presented in [372]. It is shown that

the strain-induced T

variation on defects is markedly enhanced in HTSCs due

to small ξ,highT

and strong anisotropic pressure dependence of the bulk

critical temperature [15, 81, 153, 308, 357, 501, 691, 692, 764, 773, 933, 1036,

1136, 1140, 1143]. The letter reﬂects the characteristic bell-like dependence of

on the holes concentration [1041], which changes near defects due to local

lattice distortions and electro-neutrality condition. These distortions ε(x, y)

can be quite strong, causing local plastic deformations or structure transfor-

mations around dislocation arrays, where the local holes concentration can

vary from the critical value, c

at which T

= 0 up to the optimum concen-

tration, c

which corresponds to the maximum possible critical temperature,

=maxT

(ε)inadeformed sample. This can give rise to localized su-

perconducting regions coupled by the proximity eﬀect above the bulk critical

temperature, T

. Note that the localized deformations around speciﬁc struc-

ture defects can be much stronger than those accessible in experiment by

applying uniaxial stress which is limited by the overall mechanical strength

of the sample. In this case, even the hydrostatic pressure tests show a sub-

stantial increase of T

under pressure from several degrees for optimally doped

Bi-2212 single crystals up to ∼20 K in Hg-1223 [153, 773]. The eﬀect markedly

increases in under-doped HTSCs [15].

The increasing of T

is estimated in [372] for edge dislocations, low-angle

grain boundaries and metastable linear dislocation arrays, taking into ac-

count anisotropic strain dependence of T

in the ab-plane and proximity eﬀect,

deﬁning the superconducting state at intergranular boundaries. Moreover, the

compositional changes are estimated due to the strain states, caused by de-

fects, and eﬀect of the T

variations on magnetic ﬂux pinning and magnetic

granularity.

Being dependent on the sample strain, the T

changes can be directly

aﬀected by applied stress state, which alters the dislocation distribution, GBs,

microcracks and so on. In turn, this makes the eﬀect of T

increasing dependent

on the particular deformation pre-history, which can give rise to localized

metastable superconducting states on defects above the bulk T

. For example,

maximum ΔT

is deﬁned by dislocation walls of ﬁnite length which can exist

in individual crystallites. However, these macrodefects are metastable and

can disappear after annealing or redistribution of dislocations in the remnant

strain ﬁelds.

The strains around defects can also signiﬁcantly suppress T

, especially

near dislocation walls [372] or high-angle boundaries. Depending on the direc-

tion of current, this can manifest itself either as additional pinning or weak

440 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

links because of the anisotropic ﬂux pinning typical planar crystalline defects

[366]. For the perpendicular current, J, the defect behaves as a weak link

which locally diverts J(r) as it has been observed in magneto-optical experi-

ments [832]. For parallel current, the dislocation wall enhances ﬂux pinning by

producing a deep potential well for vortices [372]. Such a well can trap many

vortices, if the length of the dislocation wall, 2L>(φ

/H)

1/2

,whereφ

the quantum of magnetic ﬂux and H is the applied ﬁeld. Moreover, the local

non-stoichiometry near GBs or dislocation arrays can signiﬁcantly increase

the strain-induced T

variations at GBs as compared to the material inside

grains.

10.2 Current-Limiting Mechanisms

and Grain Boundary Pinning

A dual role of the grain boundaries, which causes increasing of the magnetic

ﬂux pinning and, at the same time, eﬀectively block or divert macroscopic

supercurrent ﬂow is discussed in [364]. As it has been shown [205], the high-

angle GBs, microcracks, stacking faults and other planar defects can lead to

signiﬁcant decreasing of the superconducting order parameter, and thus to

diminution of connectivity of the superconducting grains. As a result, HTSCs

often demonstrate electromagnetic granularity, which causes signiﬁcant de-

crease of current-carrying properties of the superconductor [139, 354, 601, 832,

860]. Moreover, GBs in HTSC are strong current-limiting defects [597] because

of the exponential decreasing of the critical current: J

(θ)=J

exp(−θ/θ

)

across tilt GBs with the misorientation angle of θ between adjacent crystal-

lites, where θ

=4–5

◦

[205].

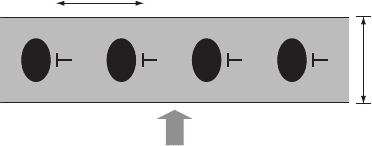
Low-angle GBs are inhomogeneous on diﬀerent scales. On a nanoscale,

they are formed by edge dislocations spaced by the distance, d = b/2sin(θ/2),

where b is the Burgers vector (see Fig. 10.2). Besides GBs, in HTSC there are

macroscopic facet structures with periods, D

∼ 100–1000

A, which are much

longer than the superconducting coherence length, ξ, along with long-range

strains and local non-stoichiometry on the scale of about D

both across and

along GBs [114].

Fig. 10.2. Channel structure of a low-angle GB formed by dielectric dislocation

core regions (black) and charge space layer (gray)

10.2 Current-Limiting Mechanisms and Grain Boundary Pinning 441

Due to the proximity of HTSC to the antiferromagnetic metal–insulator

transition, they demonstrate the strong strain dependence, T

= T

−C

−

(where C

and C

deﬁne the T

change under one-axis compression along

the a-andb-axis, respectively, for deformations ε

and ε

), which increases

into dielectric regions of the order of characteristic size b near dislocation cores.

These strain-induced dielectric core regions reduce the current-carrying cross-

section of GBs, dividing it into a set of current channels. For the anisotropic

in-plane dependence T

(ε)inYBCO(whereC

= −C

due to the eﬀect of the

CuO

chains), these channels have form, very diﬀerent from channels for the

nearly isotropic dependence T

(ε) in BSCCO crystals (for which C

= C

300 K) [373]. Moreover, the long-range deformations, caused by faceting can

lead to macroscopic modulations of T

and J

along grain boundary on the

length of order D

[114].

Another current-limiting mechanism is due to that the dislocation struc-

ture leads to an overall lattice expansion near GB in the layer of thickness

of order d, where the ion density N

is reduced by δN ∼ ζ<ε

,where

ζ ∼1–2 is Gr¨uneisen’s number [364]. The screening of the excess GB ion charge

by carriers (holes) causes the shift of the electric potential on GB, Φ

(θ) ∝ θ,

proportional to the GB dislocation density and thus the misorientation angle,

θ. This leads to the chemical potential variation at the GB, δμ(θ) ∝ θ,that

causes T

for θ ∼ 15–20

◦

. In turn, the hole depletion and zone bending near

a GB deﬁne strong superconductivity suppression in the space-charge layer

with thickness of the double Thomas–Fermi screening length, 2l

≈ ξ [373,

418, 419].

As a result, current transport through GBs is determined by the two fac-

tors: (i) strain-induced dielectric regions, which impede current ﬂow and (ii)

suppression of the superconducting order parameter in the current channels

due to charging eﬀects. When the angle θ increases, the chemical potential

μ(θ) on GB changes toward the under-doped insulating state, leading to pro-

gressive suppression of J

with θ. Calculations of J

(θ) are carried out in

[373] on the basis of the Ginzburg–Landau equations. They show that above

“transistor” model of GB describes well the observed exponential decreasing

of J

(θ) in HTSC.

The current transport in polycrystals in a magnetic ﬁeld of B is determined

by vortex dynamics and pinning, which are signiﬁcantly aﬀected by the chan-

nel structure of low-angle GBs. The increase in the misorientation angle, θ,

directly alters the structure of GB vortices. For very small θ, vortices on a

GB are Abrikosov’s (A) vortices, localized on the dielectric dislocation core

regions. At higher θ, the width of the GB current channels becomes of order ξ,

so the normal vortex core disappears turning into a Josephson core, which is a

2π-phase kink of length, l ≈ ξJ

, along GB, where J

is the decoupling cur-

rent density [364]. An intermediate Abrikosov vortex with Josephson core (AJ

vortex) [362] exists in the region of θ, where the phase core size, l, is smaller

than the London penetration depth, λ. This condition (l<λ) holds in a rather

wide region, J

/k < J

(θ) <J

,wherek = λ/ξ ∼ 100 is Ginzburg–Landau

442 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

parameter. For higher θ, J

(θ) decreases below of J

/k, and the AJ vortex

turns into the Josephson vortex of length λ

=(cφ

/16π

λJ

)

1/2

[364]. This

continuous A → AJ → J vortex transition with increase in θ directly aﬀects

vortex pinning on GB.

Vortices on grain boundaries are pinned due to both interaction with het-

erogeneities along GBs (core pinning) and magnetic interaction with GBs and

bulk A-vortices. The pinning force, f , is highly anisotropic with respect to the

current direction. If J  GB-direction, bulk A-vortices, spaced by L<lfrom

a GB are strongly pinned due to their magnetic interaction with the GB. This

causes the inverse dependence, J

∼ ξJ

/D, on the grain size, D at low ﬁeld,

B provided that GBs do not block current ﬂow, that is, J

[366]. This

behavior of J

(D) alters at higher values of B, either because the global value

of J

(B) is now limited by J

(B) or pinning becomes collective if the Larkin

pinning correlation length L

(B) >D.

When a current crosses GBs, the global value of J

in polycrystals is found

by a de-pinning of vortices, displacing along the GBs network. The core pin-

ning of such vortices is caused by their interaction with modulations of the

local current density, J

(x), which are found by current channels or facet

structure. For J

(x)=J

+ J

cos(qx), the AJ-vortices on a GB become

de-pinned, if the component of J perpendicular to the GB exceeds J



,which

is found as [832]



=2πJ

ql exp(−ql) . (10.1)

The critical current density, J



(T,B), is maximum for the optimum period

of the pinning potential, L

opt

=2πl(T,B). For ﬁxed q,theoptimumpin-

ning occurs in the region of T and B,whereql(T,B) ≈ 1. Note, that the

pinning of GB vortices parallel to the grain boundary dislocations has been

observed in [195]. However, because of the large size of the AJ phase core

(l ≈ ξJ

>> ξ), the pinning of AJ-vortices is much weaker than that of

bulk A-ﬂuxons. As a result, GBs become channels of preferential motion for

AJ- or J-vortices.

AJ-vortices, moving along the GB network experience the magnetic poten-

tial, U(x)=−φ

H(x)/4π, produced by strongly pinned bulk A-vortices. Here,

the magnetic ﬁeld along a GB varies as H(x) ≈ B + H

cos(2πx/a), where

a =(φ

/H)

1/2

in the inter-vortex spacing and the amplitude, H

≈ φ

/(2πλ)

is of the order of the lower critical ﬁeld, H

. Thus, the magnetic pinning

force, f



∼ φ

sin(2πx/a)/a ∝ H

1/2

,increaseswithH, leading to a non-

monotonous ﬁeld dependence of the global current density, J(H) (so-called

“ﬁsh-tail” eﬀect) [366] and matching peaks in the dependence, J

(H) [63].

These matching peaks have also been observed in YBCO bicrystals at ﬁelds

= φ

, for which the inter-vortex spacing is commensurate with the

GB facet structure [114].