Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

10.4 Non-Linear Current in Superconductors with Obstacles 453

diﬀerences between the current domain walls and the d-lines. First of all, the

domain walls have an internal structure and varying width, which depends

both on the value of n and on the geometry of current ﬂow. For example,

for the void in Fig. 10.10b, the width of the domain walls increases with the

distance from the void. This broadening of the domain walls provides the de-

cay of current perturbations, caused by the defect size a on a ﬁnite distance,

⊥

∼ an, much longer than a,ifn>>1. Moreover, the current domain walls

described by exact hodograph solutions remain diﬀerent from the phenomeno-

logical d-lines even in the critical state limit, at n →∞. It may be shown that

current ﬂow near domain walls satisﬁes the equation, ∇×E =0.

As the results of [367] show, a planar obstacle of size a greatly increases

electric ﬁeld disturbances over scales, L

⊥

∼ an, perpendicular to current

ﬂow or, L



∼ an

1/2

, along the current ﬂow, causing long-range interaction

between defects and strong eﬀect of the sample geometry. Indeed, even a

sparse network of planar defects can signiﬁcantly reduce the eﬀective current-

carrying cross-section if the average spacing between the defects is smaller

than L ∼ an.Fortypicalvaluesofn ∼ 30, this non-linear blockage of trans-

port current by defects can occur at rather small concentration of obstacles,

which is only a few percent of the geometrical cross-section of a supercon-

ductor. This eﬀect can have important applications for current percolation in

superconductor. For example, a microcrack in a ﬁlm with thickness, d (see

Fig. 10.9a), can cause a strong local peak of E(x) in YBCO coated con-

ductor, even for rather small defects, a>d/n<<1. In turn, such local

peaks of voltage and dissipation change the global current–voltage charac-

teristic of the whole conductor, similar to the eﬀect of macroscopic random

heterogeneities [374].

Measuring the scales L

⊥

and L



of magnetic-ﬂux disturbance, one can

estimate both the value of n ≈ (L

⊥



)

and the defect size, a ∼ L

⊥

/n.

The excessive dissipation caused by defects is another important feature of

the strong non-linearity of E(J). As a rule, HTSCs contain many macroscopic

current-limiting defects (cracks and high-angle grain boundaries), contribut-

ing considerably to the overall ac-losses and energy dissipation. For exam-

ple, for a sparse array of planar defects of size approximately a, spaced by

l>>a, the excessive dissipation per unit volume can be estimated as [367],

3/2

(a/l)

, which attains the order of the background bulk dissipation

(corresponding to uniform sample without defects) J

, if the geometrical

parameter, l<an

3/4

. Then, the overall dissipation will be stated by de-

fects, if they occupy rather small fraction ∼ n

−3/4

(of the sample geometrical

cross-section), which is few percent for superconductors with typical values

of n ∼ 20–30. The excessive dissipation due to defects can also trigger local

thermal instabilities in HTSCs [371]. These instabilities develop, mostly in

the regions of increased heat generation (for E>E

), which dominate the

overall dissipation. Other types of orientational current instabilities can be

caused by the high anisotropy of HTSCs, when current is forced to ﬂow along

454 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

(a) (b)

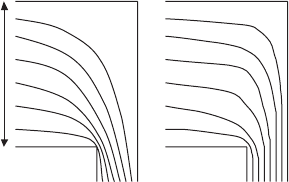
Fig. 10.11. Current streamlines for a transformer: (a) normal metal (n =1)and

(b) superconductor (n = 30) [293]

the c-axis by microcracks [115, 854] or a “brick-wall” structure of in-plane tilt

grain boundaries [104].

Equation (10.3) for steady-state current ﬂow become

∇×E =0, ∇×H = J . (10.7)

In the case of the transformer or elbow geometry (see Fig. 10.11), the

hodograph transformation method enables to compare the behavior of current

streamlines for normal metal (n = 1) and superconductor (n = 30), leading

to the important diﬀerences [293]. The metal streamlines become increasingly

compressed near the corner (J ∝ 1/x

1/2

and E ∝ 1/x

1/2

,wherex is the

distance from the corner). The current density for a superconductor is only

weakly divergent at the corner with J ∝ 1/x

1/n

(n>>1), while the electric

ﬁeld singularity is strongly increased (E ∝ 1/x). There are several similarities

with behavior, predicted by the Bean’s critical state model, namely (i) in the

limit of n →∞, the current density displays no singularities, even for ﬂow

around a sharp corner, and (ii) the current ﬂow breaks up into well-deﬁned do-

mains. At the same time, in contrast to Bean’s model, the equilibrium current

density does not remain uniform in a sample with obstructions.Figure. 10.11b

presents three diﬀerent ﬂow regions: two asymptotic regions, where current

ﬂow is straight and uniform, and an intermediate region, where the stream-

lines point radially outward, as if from a point-source, located at the top right

corner of the current lead. In this intermediate region, the current density is

not uniform, but the horizontal width of the point-source region is approxi-

mately 2L/π.

Figure 10.12 shows the current streamlines for the two current blocking

constrictions of diﬀerent sizes. In Fig. 10.12a, 90% crack shows a point-source

ﬂow domain, similar to the transformer geometry. Again, the current distur-

bance has a horizontal width of approximately 2L/π. In Fig. 10.12b, 10%

crack exhibits the long-range nature of current disturbances near obstruction.

Slightly below the defect, J is enhanced above its unperturbed value by an

average factor of about (1 + 1/n

1/2

) ≈ 1.18, for n = 30. For a defect of size

a, streamlines typically return to their unperturbed, uniform state beyond a

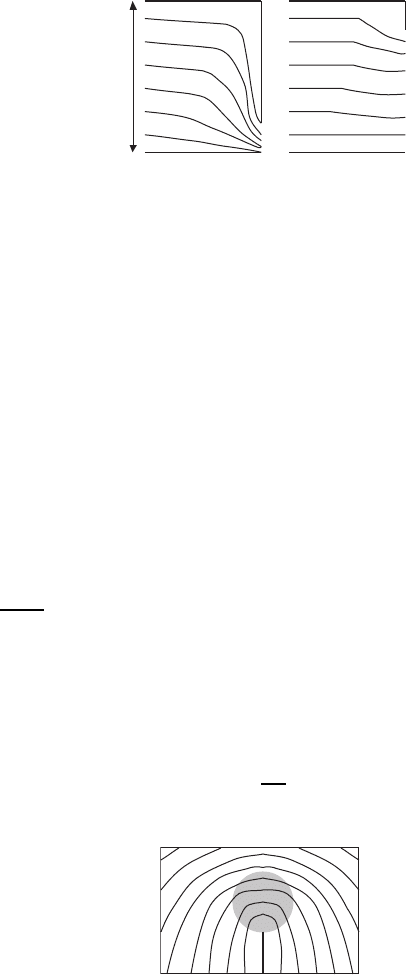
10.4 Non-Linear Current in Superconductors with Obstacles 455

(a) (b)

Fig. 10.12. Current streamlines for two constriction geometries (n = 30) [293]

characteristic length scale of an

1/2

. At the same time, signiﬁcant perturba-

tions J extend across the entire width of the sample in Fig. 10.12b. On the

opposite side from the defect, the current density is still enhanced by 9% over

its unperturbed value.

The current density for ﬁnite n has a weak singularity at the end of a

defect. Thus, a region of ﬂux-ﬂow will be nucleated, leading to detrimental

consequences for the macroscopic values of J

. Figure. 10.13 presents the ﬂux-

ﬂow boundary and current streamlines near a planar defect. For a defect with

size a, which is much longer than the ﬂux-ﬂow region, the boundary is perfectly

circular, with a radius of order (E/E

)an

1/2

,whereE

is the electric ﬁeld far

from the defect. In the limit of n →∞, the boundary just touches the end of

the defect.

In the case of current ﬂow around planar defects (high-angle grain bound-

aries, microcracks, etc.) in a ﬁlm (see Fig. 10.14) for n>>1, the distribution

J(x, y) breaks into orientational current ﬂow regions of characteristic width,

w =2



ad/π,fora<<d[368]. These regions are separated by the regions

of nearly uniform current ﬂow (presented by white color). A narrow region of

highly enhanced electric ﬁeld (gray color) extends from the defect end. In this

region, the distribution E(x) on the ﬁlm side opposite to the defect is given

as [368]

E(x)

∼

+(E

− E

)exp(−x

) , (10.8)

l =2(d − a)/

√

πn , (10.9)

Fig. 10.13. Current streamlines around a crack. Gray region represents ﬂux-

ﬂow [293]

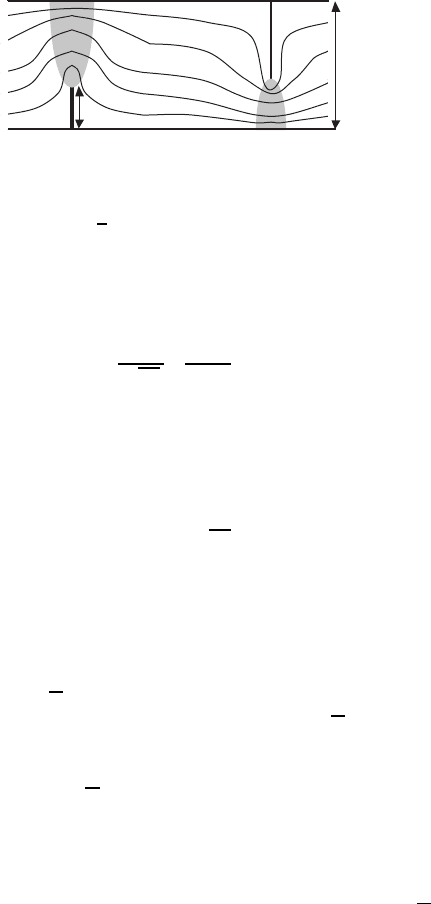
456 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

Fig. 10.14. Current ﬂow around planar defects [368]

where E

=[d/(d−a)]

√

e and E

is the uniform electric ﬁeld in the white

regions of Fig. 10.14. The narrow peaks of E(x) with width, l ∼ d/n

1/2

<< d,

and E

>> E

near planar defects give rise to the local excess voltage,

ΔV =(E

− E

)lπ

1/2

,as

ΔV =

√



d − a



n−1

. (10.10)

The factor [d/(d − a)]

n−1

,forn>>1 signiﬁcantly enhances ΔV ,even

at a<<d. As a result, a sparse array of defects, spaced by L deﬁnes the

overall voltage on the sample, when ΔV>LE

, that is, the defect size of a

exceeds a

a>a

= d[1 −



2d/

√

enL



1/(n−1)

] . (10.11)

Equation. (10.11) gives 0.1d<a

< 0.2d at 10d<L<100d,forn = 30.

Therefore, the strong non-linearity of E(J) signiﬁcantly enhances the blockage

of current ﬂow by small defects (a

<< d), even if they occupy only a small

fraction of the geometrical cross-section of a superconductor.

Finally, using a non-linear eﬀective medium theory [374], the global

averaged characteristics

J(E,B,T) of superconductors with weak macroscopic

random inhomogeneities can be calculated. In this case,

J(E,B,T) is related

to J(E,B, T) of a macroscopically uniform superconductor as [368]

J =(1− η

2/3

/2p)J, (10.12)

where inhomogeneities are quantiﬁed by a small dimensionless parameter η.

Due to the strongly non-linear behavior of E = E

exp[−U(J, T, B)/T ], the

parameter η depends on E, T and B, so even weak macroscopic random disor-

der can qualitatively alter the behavior of the global characteristic

J(E,B,T)

as compared to J(E,B,T). For example, weak heterogeneities (η<<1) can

lead to non-monotonous dependence of the critical current density J

on the

magnetic ﬁeld B (to the ﬁsh-tail eﬀect), while strongly aﬀecting the curvature

of the plot “ln E–J” [368].

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 457

10.5 Current Percolation and Pinning

of Magnetic Flux in HTSC

Experimental studies of GBs show that their critical currents (I

)couldvary

over orders of magnitude [206]. Then, it may be expected that supercurrent

ﬂow in polycrystalline samples at least near the critical state, would be per-

colative in nature that is supported by magneto-optic investigations of Bi-

2223/Ag tapes [833]. As a result, the behavior of current ﬂow in the case of

a distribution of boundaries with a suﬃciently widespread of I

may be un-

derstood. It is possible to apply the percolation theory to two directions of

superconductor’s studies:

(1) Transport in polycrystalline superconductors is characterized by links (or

breaking of those) between adjacent grains that can be described by per-

colation process [160, 191, 906 1013]. This approach is applied to sintered

HTSC bulks [98, 577, 706, 800, 819, 822], to Bi-2223/Ag tapes [785, 867,

1006] and to two-dimensional coated conductors [398, 437, 556, 903, 904,

1007].

(2) Flow of Abrikosov’s vortices through a superconductor can be also re-

garded as percolation process, which is governed physically by local trap-

ping (or untrapping) of vortices [1161, 1205].

The square [398, 556, 577, 785, 800, 819, 822], hexagonal [903, 904, 1007,

1188] and cubic [738, 867] meshes are used for diﬀerent numerical models.

On the theoretical level, percolation methods have dealt mainly with

linear circuit elements and focused on the critical behavior (i.e., on power

laws) near the percolation threshold [1206]. At the same time, the case of a

mesh of resistive elements with arbitrary non-linearity, where individual re-

sistive elements have been removed at random has been considered [1018].

It may be shown using the renormalization-group theory that the I–V char-

acteristic follows a power-law behavior near the percolation threshold. How-

ever, these renormalization-group calculations do not tell us anything about

the value of the critical current or the shape of the I–V curve away from the

critical region. The metal–insulator problem, in a certain sense similar to the

superconductor–metal problem, has been studied away from the percolation

threshold [181]. The case of a linear medium containing a small admixture of

non-linear elements has also been studied. This model is applied to the study

of composites, formed by non-linear impurities, embedded in a linear host

[613, 618, 1166]. Theoretical predictions of the I–V characteristics are made

using the Clausius–Mossotti approximation [618] or the eﬀective-medium so-

lution [1166]. Both cases are limited to the case of weak non-linearity or a low

density of non-linear elements. References [610, 611] are more close to under-

standing of the entire I–V characteristic for a strongly non-linear system. In

these works, a Ginzburg–Landau model of conduction in polycrystalline super-

conductors and a simpler model of non-linear resistor network is considered.

458 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

The latter provides a reasonable and relatively simple representation of the

physical properties of a superconductor with weak couples.

10.5.1 Model of Non-linear Resistor Network

It is assumed that the current ﬂows through a random array of microcrystal-

lites, separated by grain boundaries that act as weak links. Following [398],

we construct on the ﬁrst step an equivalent resistor network. For simplicity, it

is assumed that each grain is perfectly conducting (i.e., they are equipotential

areas). This allows one to separate, at least temporarily, the two current-

limiting factors (ﬂux pinning and weak links). Therefore, the obtained results

will be limited to cases in which the total magnetic ﬁeld (applied plus self)

is small enough that there is no ﬂux, penetrating into the grains. Flux only

penetrates the GBs.

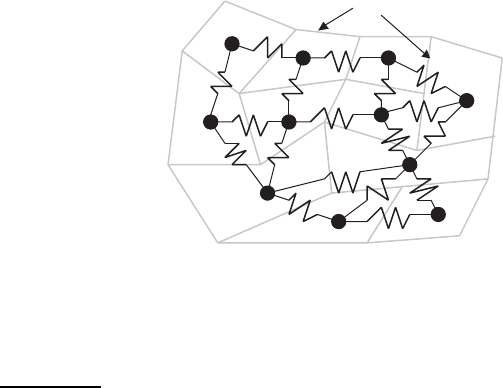
Consider the grains as nodes of above network, but replace each boundary

by a non-linear resistor (see Fig. 10.15). In graph–theoretical terms, the graph

of boundaries is replaced by its dual graph, with relation being one-to-one [28].

We shall assume that the geometrical randomness is less important than the

randomness in the strength of the resistors.

Investigate the current ﬂow through a granular superconductor, focusing

on two models of the GBs, applicable to the cases of Josephson junctions in low

and in high external ﬁelds, respectively.

Each boundary is found by its I–V

characteristic. V is some non-linear function of I for every resistor, but each

resistor may be diﬀerent. Generally, the resistors are described by a probability

distribution, P [V (I)]. Consider, for better understanding of the results, binary

distributions consisting of a mixture of weak and strong couples, which are

Fig. 10.15. The reduction of a polycrystalline superconducting network to an equiv-

alent resistor network. The irregularly shaped regions are superconducting grains

taken as equipotentials. All potential drops take place across GBs, shown as non-

linear resistors [398]

Why actual boundaries should behave in this way is explained in [630].

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 459

identical to each other in each group. The corresponding concentrations of the

links are denoted by p and q =1−p.

Divide the present model into two kinds corresponding to (i) weak-ﬁeld

Josephson junction (JJ) and (b) strong-ﬁeld ﬂux-ﬂow (FF) boundaries.

Binary JJ model. For the JJ case, the weak (strong) links with corresponding

concentration, p(1 − p), have a critical current, I

). If I<I

in such

resistor, then V =0;ifI>I

,thenV = IR

,whereR

=const(i =1, 2) and

.NotethatV is a discontinuous function of I for both types of links

(see Fig. 10.16).

Binary FF model. For the FF case, the weak (strong) links with corresponding

concentration, p(1 − p), have a critical current, I

). If I<I

in such

resistor, then V =0;ifI>I

,thenV =(I − I

,whereR

=const(i =

1, 2) and I

. Here, V is a continuous function of I for both types of

links (see Fig. 10.16).

Both models diﬀer at microscopic scale. The JJ model represents a situa-

tion of low current, and zero applied ﬁeld. The Josephson junction is assumed

to be superconducting for small currents and normal at high currents, when

the voltage drop is just ordinary Ohmic loss. There is a discontinuous change

between the two regimes. The FF model is intended to simulate weak links

because ﬂux pinning in them is weak. In this case, I

of the link represents

the de-pinning current. The losses take place for I>I

at the movement

of ﬂux along the boundary. Experimental measurements on individual GBs

show a crossover between the two sorts of behavior. Figure 10.17 shows I–V

characteristics for a 10

◦

-GB. At low applied ﬁeld, the boundary behavior is

similar with the JJ model, while at high ﬁeld it is closer to the FF model.

The considered non-linear network canbeanapproximationtoanactual

JJ array in the over-damped limit. The JJ model can represent a set of over-

damped junctions with no pinning, in which the McCumber parameter, β

≡

R

/(2eI

1/2

< 1, where R and C are the resistance and capacitance

of the junctions. Then, output I

tot

represents the dc-component of the actual

output value of real over-damped junctions. In turn, the FF model is the case,

where pinning of Josephson vortices dominates the transport. The result of

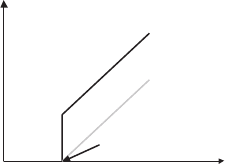
Voltage

Current

JJ model

FF model

Critical Current

Fig. 10.16. I–V characteristics for Josephson junction (JJ) and ﬂux-ﬂow (FF)

models. The ﬁrst is considered to be appropriate for low ﬁelds and the second for

high ﬁelds [398]

460 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

100

0.1

0.01

Current Density (A/cm

)

Voltage (μm)

3 0.5 0 T

10°

Fig. 10.17. Proper behavior of test I–V characteristics for 10

◦

-GB in YBCO at

diﬀerent applied ﬁelds. At low ﬁelds, the I–V characteristic is similar with the JJ

model. As the applied ﬁeld increases, there is a crossover at 5.5 T to a behavior that

is similar to the FF model [398]

numerical realization of two models is V

tot

) dependence for the system as

a whole. Thus, we feed a ﬁxed current at one end and collect it at the other

and measure the voltage drop.

Let there be a distribution of non-linear resistors on an inﬁnite mesh,

where each resistor have some critical current and occupation probability.

This implies that the critical current can be found as

tot

=min

l∈S

(l)

, (10.13)

where the minimum is taken over all surfaces that separate the electrodes

[883]; l are the wires that pierce S and I

(l)

is the critical current of wire l.

Because I

tot

depends only on I

(l)

, (10.13) states the dependence of total crit-

ical current of the mesh only upon the critical currents of individual elements

and not upon their dissipative behavior at I>I

Consider two adjacent inﬁnite surfaces S and S

∗

, which separate the elec-

trodes. The maximum supercurrent that can be carried through S,considered

entirely by itself, is:

(∞)

. (10.14)

However, it is not clear that the current can penetrate from S to S

∗

Indeed, we expect the critical current of the inﬁnite mesh to be less than

(∞)

, deﬁning an upper bound for I

tot

, independent of model and system

dimensionality.

In order to obtain a better approximation for I

tot

, consider a binary model,

in which there are only two types of resistors (I

and I

) with occupation

We take a mesh constant of unity to avoid distinguishing between currents and

current densities.

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 461

probabilities, p and q =1− p, respectively.

Equation (10.14) for this model

gives

tot

= pI

+ qI

. (10.15)

Consider M × N square mesh and suppose there is a current, I>NI

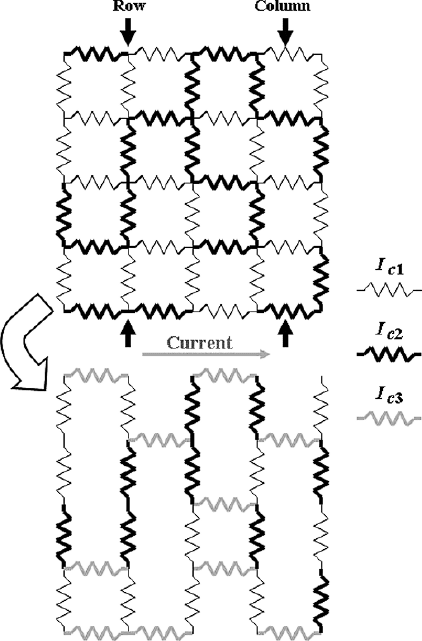
transported horizontally across the mesh. Divide the resistors into two groups.

Those resistors, which dispose perpendicular to the average current ﬂow direc-

tion, are called by “row resistors”. These rows are connected by what we will

call “column resistors”, that is, the resistors dispose parallel to the current di-

rection (see Fig. 10.18). The current ﬂow can be considered as a superposition

of two current distributions: NI

, running directly through the mesh (along

the column resistors) and a percolating current, I − NI

. Considering the

percolating current, we can “subtract oﬀ” an I

resistor from each column re-

sistor (a modiﬁed dilute resistor network is shown in Fig. 10.18). The columns

of this lattice have holes with probability, p,andI

= I

−I

critical current

resistors with probability, q =1−p. This modiﬁed mesh has a critical current,

. Then, the total critical current is I

tot

= I

+ I

The value of I

is found by two factors. First, the amount of current that

can be transported across any given column of the mesh, and second, whether

or not that current can be re-distributed to the I

resistors in the next column.

There are two various regimes of behavior distinguished by whether I

is less

or greater than I

When I

(or I

< 2I

), it is easy enough to re-distribute the

current between columns. Any current ﬂowing through a column resistor can

be shunted sideways along a row and re-distributed to the next column as

long as another column current does not get in the way. We can approximate

the probability that a given column current can be re-distributed along a row

without being interfered with in the following fashion. It is equal to the prob-

ability that there is an I

resistor directly across the given column current,

plus the sum of probabilities that there is a path at a site s steps along the

row, and no paths either coming in or out of the row before that point. By

only summing over steps to the right (or left) of the given column current,

we avoid the problem of interfering with the paths of other incoming column

currents. This re-distribution probability can be written as [398]

= q

∞

s=0

(1 − q)

2q − q

. (10.16)

Taking into account a volume fraction q of I

row currents, we write down

the averaged critical current density as

tot

= I

+(I

− I

)qp

= I

+(I

− I

) ×

2q − q

. (10.17)

Because, it is considered only the critical current, the exact I–V characteristic of

these resistors is unimportant.

462 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

Fig. 10.18. Scheme of two-dimensional network for current ﬂowing to the right.

Resistors are divided into those parallel (column) and perpendicular (row) to the

current. Then, the actual mesh is reduced to a dilute network, subtracting out a

uniform current to the right [398]

The obtained approximate formula (10.17), in particular, neglects the pos-

sibility that the percolation current goes backward. However, we expect this

path to make a smaller contribution than the ones calculated, because it cor-

responds to relatively rare conﬁgurations of resistors. In particular, approxi-

mation (10.17) should be well for the inﬁnite mesh, if I

[398].

When I

, the presented calculation will fail, because it is no longer

easy to shunt the current sideways along a row of resistors and hence the re-

distribution probability will be diﬀerent. Similar to above, a diﬀerent critical

current is calculated as [398]

tot

= I

+ q[I

− p

∗

)+(I

− I

∗

] , (10.18)