Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 473

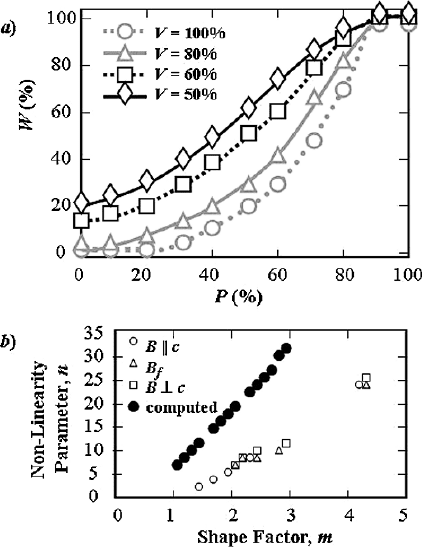
Fig. 10.25. (a) Change of degree of broken columns (W ) as a function of probability

of the broken links (P ) for system, including V % superconducting elements, and (b)

change of non-linearity parameter, n, as a function of distribution shape factor, m

[784]. The computational results (black circles) are compared with experimental data

(white ﬁgures) [875]

Figure 10.25a shows W in dependence on P for M = 400,N = 1000,C =2

and variation of V from 50 to 100%. In the case of V = 100%, the fraction W

of broken columns starts to increase for P>20%, that means a generation

of an electric ﬁeld. For V = 60%, W has already ﬁnite value even for P =0.

After calculation of E–J characteristic, so-called non-linearity parameter, n,

is found. As it is shown in Fig. 10.25b, the dependence of n on m,calculated

in the considered model, has a similarity with the experimental results [875].

Other approach, based on the statistical distribution of critical current

density and used for study of non-linear E–J characteristic, is developed in

[1161]. According to this model, the de-pinning probability function (Q)can

be described as a function of current density (J) by the next expression:

Q(J)=[(J − J

)/J

]

, (10.40)

where J

is the percolation threshold identical to the minimum value of J

; J

is the scale parameter, representing half-width of the statistic J

distribution;

474 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

and m is the distribution shape parameter. Then, the E–J characteristic can

be obtained integrating Q(J)as

E(J)=ρ



[(J

− J

)/J

]

, (10.41)

where ρ

is the resistivity for the uniform ﬂux ﬂow [1161]. In particular,

this model has permitted to estimate inﬂuence of bending strain on transport

E–J characteristics for Bi-2223 Ag/AgMg-alloy-sheathed tape [549]. More-

over, this approach permits to separate the components, caused by the grain

connectivity and ﬂux pinning, originated from the bending strain.

10.5.4 Aging at Mechanical Loading

In design of energetic HTSC cables, an estimation of electric properties of

the current-carrying elements presents the signiﬁcant interest at mechanical

aging of the sample, that is, at long cyclic and static loads. A probabilistic

approach is one of the main methods for the solution of this problem [719,

720]. The V –I characteristic can be described, using the Weibull’s distribu-

tion, and the time behavior of the relevant parameters can be considered

during mechanical aging of the cable material, for example, under tensile

stress and bend-vibration. In order to model the sample behavior, a proba-

bility function, g(J

), is introduced, which describes the probability that a

cross-section of a superconductor has a given value of the critical current den-

sity, J

[67]. It has been shown that g(J

) could be analytically derived as

the second derivative of the E–J characteristic via ﬂux-ﬂow resistivity. This

relationship holds, however, for a pure superconductor of type II, that is,

neglecting eﬀects of any non-superconducting matrix. Determination of second

derivative of E–J characteristic can be found numerically [1135]. A best-ﬁtting

distribution must be chosen in order to obtain parameters, which are able to

describe the function g(J

), as well as its integral, that corresponds to the cu-

mulative probability, G(J

). The probability function considered below is the

two-parametric Weibull’s distribution, which ﬁts both skewed and unskewed

probability density characteristics. The expressions of the two-parametric den-

sity and cumulative-probability Weibull’s function are found by [527]

F (x)=1− exp[−(x/α)

]; (10.42)

f(x)=(β/α)(x/α)

β−1

exp[−(x/α)

], (10.43)

where α and β are scale and shape parameters, whereas the random variable

x corresponds to the critical current density J

The Weibull’s parameters can be estimated in several ways [112]. In par-

ticular, they can be calculated on the base of test data, obtained by the prime

derivative of the E–J characteristic, that is, G(J

), numerically performed

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 475

and plotted in the coordinate system lg{−ln[1 − F (x)]} in dependence on

lg(x), which linearizes (10.42), transforming it into a straight line of slope β.

Actually, this probabilistic approach should be only applied to data rel-

evant to the superconductor, while the tested samples have a silver shield,

whose contribution is not easily separable from that of the superconductor

body. Therefore, the Weibull’s function can be used only to the experimen-

tally obtained V –I characteristics with the aim to show how it is correlated

with mechanical stress aging.

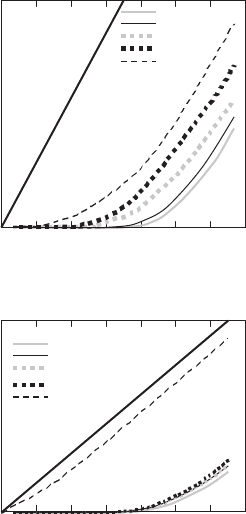
Examples of V –I characteristics, measured in aged and unaged specimens

are shown in Fig. 10.26 for vibrated and tensile-stressed samples. The silver

shield V –I characteristic is also presented in Fig. 10.26 for the sake of compar-

ison. As it is followed from this, the mechanical aging process can signiﬁcantly

aﬀect V –I characteristics. Moreover, the V –I curves tend to the silver resis-

tance for values of currents monotonously decreasing as aging time increases.

−

1200

1000

800

600

400

200

−

0 min

80 min

160 min

240 min

320 min

Current (A)

Voltage (μV)

(a)

2500

2000

−

1500

−

1000

−

500

−

0 min

139 min

248 min

379 min

540 min

Current (A)

Voltage (μV)

70605040302010

(b)

Fig. 10.26. V –I characteristics at various aging time for cases of vibration aging

(a) and tensile-stress aging (b) [720]

476 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

Tensile stress and vibration do age specimens in a diﬀerent way. While

the former creates local damage cracks only, the latter leads to overall degra-

dation, when silver shield is no more able to endure the applied stress. This

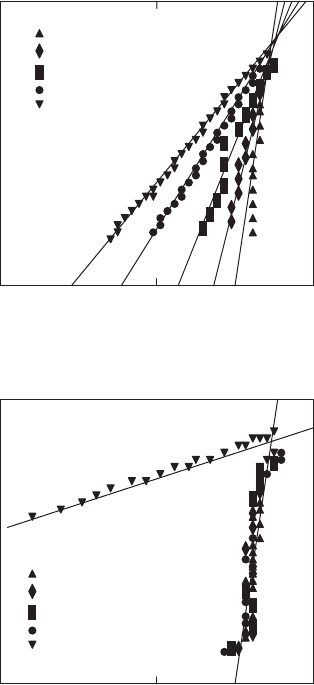
approach permits to obtain the Weibull’s functions for cases of cyclic and ten-

sile loads (see Fig. 10.27 [720]) with the normalization factor, deﬁned by the

silver characteristics. Moreover, the scale and shape parameters (α, β)ofthe

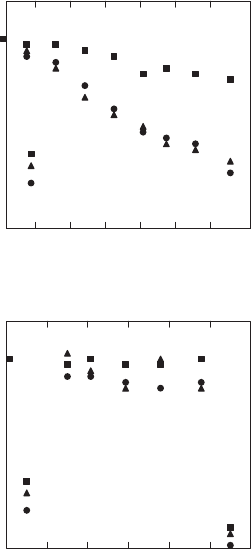
Weibull’s distribution can also be estimated and plotted as a function of aging

time (see Fig. 10.28 [720]). Figures 10.26–10.28 permit to estimate eﬀects of

the aging level and type on electrical properties of superconductor. So, the

−

99.9

−

Current (A)

Probability (%)

0 min

80 min

160 min

240 min

320 min

(a)

(b)

−

99.9

1 100

−

Current (A)

Probability (%)

0 min

139 min

248 min

379 min

540 min

1 10010

Fig. 10.27. Weibull’s plots derived from normalized prime derivative at diﬀerent

aging times for cases of vibration aging (a) and tensile-stress aging (b)

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 477

−

1.2

1.0

0.8

0.6

0.4

0.2

0.0

β/β

α/α

β/β

−

1.2

1.0

0.8

0.6

0.4

0.2

0.0

−

(a)

(b)

−

Time (min)

0 350300250200150

100

Time (h)

0 600500400300200100

Fig. 10.28. Relative values of scale (α)andshape(β) parameters of the Weibull’s

distribution and also of critical current density (J

)vstime(t), for one sample in

the case of aging due to vibration (a) and tensile stress (b)

critical current (I

) at moderately high and low cumulative probability signif-

icantly decreases as aging time increases, sharply in the case of tensile stress,

progressively for vibration. Similarly, the value of β signiﬁcantly diminishes

with time, reaching the lowest values for the most aged samples.

10.5.5 Eﬀective Electrical Conductivity

of Superconducting Oxide Systems

Finally, based on the percolation theory, we consider current carrying in the

model HTSC systems of YBCO and BSCCO, investigated in Chap. 8, and

also study corresponding eﬀective characteristics. Comparison of the results

of fracture resistance alteration due to action of diﬀerent toughening mecha-

nisms, with qualitative features of electrical conductivity, stated in this section

478 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

permits to estimate an eﬀect (positive or negative) of microstructure features

on properties of the considered superconductors.

YBCO Ceramic

It is known that electrical conductivity (the inverse value of resistivity) in

non-ordered media is proportional to the self-diﬀusion factor, and hence, the

average quadratic deviation of the liquid particles in absence of an external

force [332]. Following [800], consider the YBCO model structure as a perco-

lating cluster with cells, occupied by grains, and by free cells, corresponding

to voids. Obviously, the percolating (or conducting) properties decrease due

to the existence of intergranular microcracks and porosity. However, it is also

clear that all model structures considered below, stated in Chap. 8, possess a

joining, percolating cluster, because the following inequality always fulﬁlls:

+ f

<< p

, (10.44)

where C

= N

/N is the closed porosity of the ceramics (N

is the cell number,

occupied by voids and N is the total cell number); f

= l

is the ratio of

the cracked facets to the total number of boundaries between cells of the

joining cluster (obviously, f

= l

,wherel

is the total length of the

intergranular boundaries, because l

); and p

=0.5927 is the percolation

threshold for a square lattice.

In order to estimate eﬀective electrical conductivity of the model struc-

tures (considered in Sect. 8.1.1 and 8.1.2), we modify a known algorithm,

called ant into maze, applied for diﬀusion description in irregular media [332].

Take into account together with crystallite phase and voids, an existence of

grain boundary microcracks, and also GBs, possessing a smaller conductivity

compared to intracrystalline space. Consider a chance movement on only oc-

cupied cells (on crystallite phase) of the percolating cluster. At any time, the

probable numbers, p

∈ [0, 1] (where k =1,...,4) are generated in all cells,

which are adjacent to the main cell. In the case, when the cell under consid-

eration is separated from the main cell by a GB then its probable number is

decreased by 0.1 (to design the predominant cluster growth within a grain). If

an intergranular boundary has been replaced by a microcrack or the adjacent

cell is a void, then the corresponding probable number is found to be zero.

The cluster growth results from the occupation of a cell with largest possible

number, p

≥ p

. The cluster growth is impossible when the initial cell is

surrounded by voids, microcracks or when all of p

. Next, all the process

is repeated. At each step, including a marking time, the value of t increases

by 1. In the time, t = 0, some chance cell of the joining cluster begins to

Similar modeling can be fulﬁlled at other regular lattices having the following

values of the percolation threshold, p

, and the shape of unit cell [1075]: 0.6970

(hexagon), 0.5 (triangle), 0.4299 (diamond), 0.3116 (cube), 0.2464 (b.c.c.), and

0.1980 (f.c.c.).

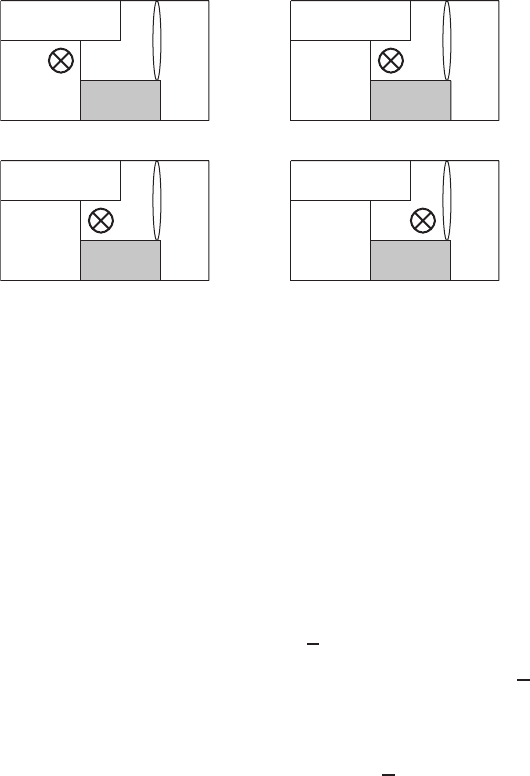
10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 479

0.58

0.26

0.43

(0.33)

0.75

(0.65)

0.00

0.18

(0.08)

0.00 0.00

0.94

0.71

(0.61)

0.32

(0.22)

0.46

0.66

(0.56)

0.53

0.00

0.80

(a)

(c)

(b)

(d)

0.00

Fig. 10.29. An example of percolating cluster growing in YBCO ceramic. Numbers

denote probabilities of cell occupation (in brackets there are considered probabilities,

taking into account a priority, which are compared with percolation threshold, p

0.5927). A cross corresponds to the cluster cell at previous step. Microcracks, formed

during cooling, are shown at GBs; porosity is denoted by gray color

move. In time t, the square of distance between initial and ﬁnal sites is calcu-

lated. Then, the modeling is repeated several times, and the mean quadratic

displacement, R, associated with the conductivity of the modeled structure is

calculated. An example of the cluster growth is shown in Fig. 10.29.

Statistically reliable results are obtained by applying the stereological ap-

proach. We obtain, again a necessary number of realizations for the statistical

process to ﬁnd unskewed estimation of the considered stereological character-

istic as [145]

n = (200/y)(σ

/x) , (10.45)

where y is the accuracy level (in this case 10%); σ

is the variance; x is the

mean value of the stereological characteristic. At the study of the electric con-

ductivity process, ﬁrst a growth of a joining cluster on the type of occupying

percolation [332] in two-dimensional lattice (25 × 40 cells), forming a path

from left to right of its boundary, is considered. As

x, we select the lattice

width (= 40), and the value of σ

is calculated by corresponding exceeding of

the cluster cell number over lattice width.

The percolation properties of the model microstructures, estimated for

t = 100, are presented in Table 10.1. The normalized mean quadratic dis-

placement, R/R

(where R

is the corresponding value for non-porous mate-

rial), which is proportional to electrical conductivity decreases with growth

of initial porosity as well as the square (cell number) of the joining cluster,

S/S

is the cluster area for nonporous material). These data correlate

with increasing GBs, l

, at the enhancement of the initial porosity, C

and decreasing of mean grain size, obtained in [814]. Thus, introducing even

small priority for growth of the joining cluster within grain compared to its

480 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

Table 10.1. Some model parameters for YBCO ceramics of various structures

Properties C

=0% C

= 20% C

= 40% C

= 60%

0.503 0.523 0.557 0.630

S/S

1.000 0.956 0.872 0.644

R/R

1.000 0.866 0.846 0.785

propagation in adjacent one (in this case, it corresponds to enhancement of

probability by 0.1) correlates with experimental data and leads to qualita-

tive conﬁrmation of known results by the results of computer simulation. The

presented results point again an important role of GBs and need to obtain

coarse-granular YBCO structures. More accuracy estimations can be obtained

in the framework of this model under condition of quantitative description of

the diﬀerence of conductive properties in grain and through GB. Obviously,

they will depend on features of domain structure of single crystallites, GBs

continuity, secondary phases and so on.

Large-Grain Melt-Processed YBCO

Taking into account the model structures of the melt-textured large-grain

YBCO samples, investigated in Sect. 8.3, it is obvious that their transport

properties are found by the existence of non-superconducting (211) and su-

perconducting (123) phases, and also by GBs. Then, in the electrical conduc-

tivity model, presented in the previous section, only one position is added,

namely in the case of the adjacent cell occupation by the 211 particle, the

probable number is replaced by zero. An example of the cluster growth is

shown in Fig. 10.30, but the obtained numerical results are presented in

Table 10.2 [822].

A comparison of the obtained eﬀective characteristics with the model re-

sults of Sect. 8.3 (see Table 8.7) shows a correlation between the mean pinned

grain area,

S, superconducting ﬁeld per grain, S

and ratio of the total inter-

granular boundary length to the total number of GBs between cells of joining

cluster, l

, on one hand, and change of the seed area, on the other hand.

The percolation properties have been calculated for t = 100. The behav-

ior of the mean quadratic displacement, R/R

, and the joining cluster area,

S/S

(where R

and S

are the corresponding values for the case, f =0.0and

Table 10.2. Numerical results

Property f =0.0,

≈ 2S

f =0.0,

≈ 3S

f =0.1,

≈ 2S

f =0.1,

≈ 3S

f =0.2,

≈ 2S

f =0.2,

≈ 3S

0.325 0.235 0.133 0.116 0.111 0.136 0.099 0.083

R/R

0.803 1.000 0.649 0.816 0.865 0.452 0.473 0.544

S/S

0.979 1.000 0.929 0.957 0.979 0.893 0.900 0.921

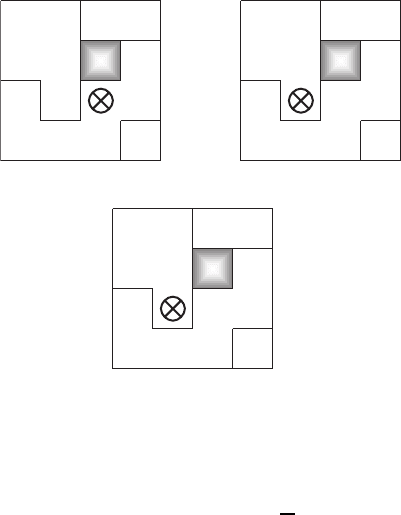
10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 481

0.30

0.95

(0.85)

0.69

0.00

0.66

(0.56)

0.18

(0.08)

0.39

(0.29)

0.78

(0.68)

0.59

(0.49)

0.24

(0.14)

(a) (b)

(c)

0.52

0.73

Fig. 10.30. An example of percolating cluster growing in large-grain YBCO sample.

Numbers denote probabilities of cell occupation (in brackets there are considered

probabilities, taking into account a priority). A cross corresponds to the cluster cell

at previous step. Gray color shows 211 particle

≈ 3S

), as well as the change in the value of S

coincide with experimen-

tal data [318, 640]. We conﬁrm that YBCO conducting properties decrease

with increase in the fraction of the 211 normal particles and with decrease in

the seed. At the same time, the considered toughening mechanisms intensify

(that in turn, inﬂuences indirectly an increasing of current-carrying proper-

ties) with an increase of the 211 normal particle size and fraction into 123

superconducting matrix. Finally, note that for completeness of investigation

of the percolation properties in this case, it is necessary to take into account

the GB microcracking during cooling and misorientaion of grain boundaries,

which are caused by indirect eﬀects of dispersed phase and also contribute in

ﬁnal superconducting properties.

Eﬀect of Microstructure Dissimilitude

The transport properties of the YBCO model structures, considered in

Sect. 8.4, are caused by superconducting granular phase, voids, microcracks

and GBs. Again, based on the algorithm ant into maze [332], eﬀective char-

acteristics can be calculated, which are presented in Table 10.3 [819]. An

example of the cluster growth is shown in Fig. 10.31.

The numerical results show a correlation between the grain area and the

ratio of total intergranular boundary length to total number of boundaries

between cells of the joining cluster, l

. The percolation properties have

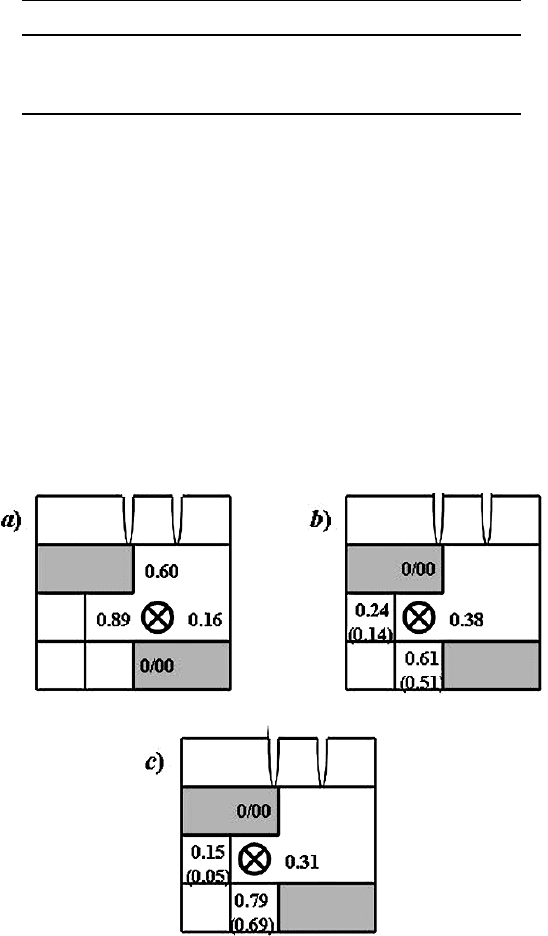
482 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

Table 10.3. Numerical results

ν,

◦

C/h l

R/R

S/S

10 0.51 1.00 1.00

20 0.50 0.91 0.87

30 0.39 0.81 0.74

been calculated for t = 100. The behavior of the mean quadratic displace-

ment, R/R

, and the joining cluster square, S/S

(where R

and S

are the

corresponding values for the case ν =10

◦

C/h), as well as a change of the value

of l

coincide with test data [642]. Thus, it is conﬁrmed that YBCO super-

conducting properties diminish with increased heating rate. This corresponds

also to the trends in the changes of the speciﬁc fracture energy (γ

(1)

/γ

(0)

)and

the microstructure dissimilitude (ΔK

/ΔK

), following from Fig. 8.33.

BSCCO Bulks

Considering the Bi-2223 model structure as percolating cluster with cells,

occupied by grains, note that the percolation properties are found in this

case by GBs, microcracks and texture, describing a connectivity of adjacent

Fig. 10.31. An example of propagation of percolating cluster in the case of

microstructure dissimilitude. Numbers denote probabilities of cell occupation

(in brackets there are considered probabilities). A cross corresponds to the clus-

ter cell at previous step. Gray color shows voids; microcracks are presented at GBs