Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 463

where

∗

= q

∞

s=0

1 − p

. (10.19)

Then, assume that the distribution of resistive elements is known for a

non-linear resistor network. A voltage drop (which will be calculated below

for the entire mesh) occurs if a current is imposed across the network. The

correct distribution of currents in the mesh can be found by solving Kirchoﬀ’s

equations, which uniquely deﬁne the current distribution in the network. In a

network of linear resistors, this reduces a set of linear equations to solution,

for which there are many standard methods. We are not aware of any general

method for non-linear resistors. The method, developed in [424, 610, 611], can

be applied only for the JJ case. The approach for the study of any current

densities, which is used below, satisﬁes current conservation and transport the

imposed current across the mesh.

We begin the solution of this problem, choosing a distribution that is

thought to be close to the actual one. This choice must conserve current at

each mesh node and also transport the imposed current across the lattice. One

possibility would be a distribution where the current ﬂows uniformly through

the mesh. Obviously, this initial approximation needs to be modiﬁed. We do

this by superimposing circulation currents on top of the initial distribution as

shown in Fig. 10.19. While these circulation currents contributes nothing to

the net transport of current they change the current path. Current conserva-

tion is obviously satisﬁed for all values of the circulation currents, which we

will consider as free variables. Thus, the search method can study all possible

currents.

The requirement to calculate the current distribution, satisfying the voltage

Kirchoﬀ’s law, can be expressed in terms of a minimization principle. If, for

a given resistor, we deﬁne the quantity



(i)di, (10.20)

Initial Guess

Circulation

Current

Fig. 10.19. Initial guess for the current distribution and imposition of circulation

currents [398]

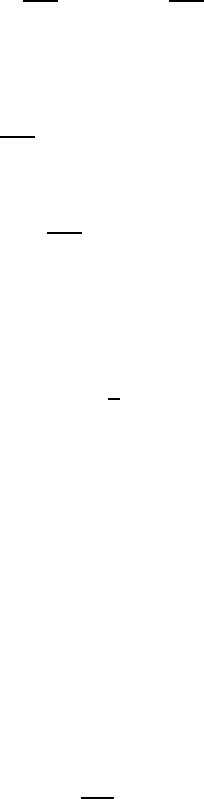
464 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

where V

(i) is the voltage-current characteristic of the j-resistor (assuming to

be known) and I

is the current ﬂowing across the j-resistor, then the solution

of Kirchoﬀ’s laws is equivalent to minimizing

G =

, (10.21)

where the sum is over all resistors in the lattice. We prove this by varying

G with respect to the currents in such a way that current conservation is

preserved. With this aim, ﬁnd a variation of G with respect to a circulation

current:

δG

δC

V (I

)

δI

δC

=0. (10.22)

Because the circulation current, C

, ﬂows around a speciﬁc loop, variations

in C

only aﬀect the currents along that loop. An additional eﬀect to be unit

linear in C

δI

δC



1, for I

on k loop ;

0, otherwise ,

(10.23)

where the sign is positive in the direction of C

. Then,

δG

δC

j∈loop

=0. (10.24)

This equation is valid for any loop in the mesh, that is, the minimization

of G with respect to the circulation currents is equivalent to the solution of

the Kirchoﬀ’s voltage law. Note that, in the case of linear resistors, G reduces

to representation

G =

Thus, for the linear case or any network, where all the voltages have the

same power-law dependence upon current, the minimization of G is equivalent

to minimization of the power loss of the mesh (a familiar result). An equivalent

minimization principle for an applied voltage can be formulated, minimizing

the sum:



(v)dv, (10.25)

where the sum is over the resistors and the free variables are the voltages at

each node [1018].

In order to understand what the eﬀect ﬁnite size has on the critical cur-

rent, consider a binary model on a square lattice. Equation (10.14) states the

bounds for an inﬁnite mesh as

≤

tot

≤ pI

+ qI

. (10.26)

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 465

At the same time, this upper bound decreases for a ﬁnite mesh. We have

for M × N lattice of nodes a resistor mesh with M = N − 1 columns and

N resistors in each column (see Fig. 10.18). Investigate possible ﬂuctuations.

The occupation probabilities may be p and q =1− p. However, obviously,

there are great ﬂuctuations from average values in a smaller mesh. Calculate

the expectation value for the maximum number of I

resistors in any of the

M columns. This value deﬁnes the limiting factor for the critical current. In

order to ﬁnd this expectation value, it is necessary to know the probability

P (a) that the maximum number of I

resistors in any of the M columns is

equal to a (out of N).

First, deﬁne f (a) to be the probability that a speciﬁc column has a resistors

of the I

-type in it:

f(a)=

a!(N − a)!

(1 − p)

N−a

. (10.27)

Then, deﬁne P

(x, a) as the probability that x columns (out of M )have

a resistors of the I

-type in them:

(x, a)=

x!(M − x)!

f(a)

[1 − f(a)]

M−x

, (10.28)

where 0 ≤ x ≤ M. Finally, the probability P (a)isgivenas

P (a)=

⎧

⎪

⎨

⎪

⎩

x=1

(x, a)

i=a+1

M−x

(0,i)],a= N ;

x=1

(x, a),a= N.

(10.29)

The obtained equation states the probability that x columns in M have

a resistors of R

multiplied by the probability that there are no columns (in

the M–x remaining) that have more than a resistors of R

in them, summed

over x. Then, we use P (a) to calculate the expectation value of a:

a =

a=0

aP (a)

a=0

P (a)

. (10.30)

Finally, we get the critical current for the mesh as

tot

+(N − a)I

. (10.31)

The present analysis is only relevant for small lattices, because for very

large meshes

a will be very close to p. Thus, the critical current is limited by

the ﬁnite size of the mesh and in that the critical current for the inﬁnite case

would be larger.

466 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

2.5

2.0

1.5

1.0

0.5

0.0

JJ model

FF model

Current

Voltage

0.5 1.0 1.5 2.0 2.5 3.0 3.50.0

Fig. 10.20. Comparison of I–V characteristics for binary JJ and FF models on

10 ×10 percolative mesh. Both models possess the same distribution of microscopic

critical currents and normal state resistances (p =0.5,I

=0.75 and R

0.75). The shape of the individual circuit elements I–V characteristics is preserved,

when they are combined into a mesh

The most important result of the computational realizations is that the

overall shape of the individual elements I–V characteristics is preserved when

the elements are combined into a mesh. Figure 10.20 compares 10 × 10 mesh

composed of JJ resistors with one of FF (p =0.5,I

=0.75 and R

0.75 in both cases) [398]. Obviously, the resulting overall characteristics are

very diﬀerent. This in itself is not surprising as the individual components have

various properties. However, the fact that the overall characteristics should

resemble that of the individual elements so closely is surprising. Statistical

averaging, even with strong non-linearity, does not wash out the underlying

input.

10.5.2 Simulation of Current Percolation and Magnetic Flux

in YBCO Coated Conductors

Despite great progress in texturing of the HTSC layer, grain boundaries re-

main the current-limiting factor. It has been shown in tests that dissipation

processes have been accompanied by viscous vortex ﬂow through low-angle

GBs [430]. Magneto-optical studies on coated conductors (CCs) state the

mechanism acting in these materials. Based on this, the model [271] uses the

simple, piece-wise linear I–V curve of low-angle GBs to calculate the global

percolative current transport in CC. Note also that most of the CC simula-

tions are reduced to ﬁnding the onset critical currents (I

) using calculations

of “limiting current path” [556, 903, 904, 1007].

A method, which enables to calculate current and ﬂux distribution as well

as I–V curves of two-dimensional grain lattices (square or hexagonal) with

arbitrary morphology and GB critical current distribution, is presented in

[1007]. Two-dimensional consideration of the current ﬂow in a CC is a good

approximation, because the thickness of the HTSC layer is much smaller than

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 467

the other length scales, and the high degree of sample texture ensures that

the current ﬂows essentially within the ab-planes. The CC is described in this

model as a resistor lattice, namely each GB is represented as a pair of resistors,

one of them with zero resistance, but ﬁnite current capacity (determined by

the GB critical current), and the second one possesses resistance proportional

to the ﬂux ﬂow resistivity.

The GB critical current is found from the GB

misalignment angle using an exponential dependence with a plateau at low

angles [1188]:

(α)=



exp[−(α − α

)/α

], for α ≥ α

;

, for α ≤ α

(10.32)

where L

is the length of the GB; α

and α

are the critical angles.

Analytically, this problem is reduced to a solution of a set of linear equa-

tions and inequalities for the currents. This set includes the current-limiting

equations for the superconducting resistors, the Kirchoﬀ’s equations for each

grain and each current loop and also equation for the total current in the con-

sidered system. This system of equations is under-determined in all non-trivial

cases, that is, there are fewer equations than variables. It is solved, simultane-

ously minimizing the total dissipation in the lattice for a given current. This

type of mathematical problem is well known in economic analysis and can be

solved by standard methods of linear optimization [393, 752].

The considered method enables to analyze both experimentally measured

grain morphologies and model structures and sets of hexagons or squares.

The former can be potentially used to predict the performance of a CC from

the morphology of its substrate. At the same time, simple model structures

are very valuable for fundamental studies of CC properties [903, 904]. As a

result of experimental analysis of the grain distributions [1188], there is a

possibility of the branching of ﬂux channels and also three scaling regimes

of I–V characteristics are identiﬁed, namely (i) the onset superconducting

current, I

, is dominated by ﬁnite- size scaling; (ii) the intermediate currents

are stated by percolation (or power-law) scaling; and (iii) the high currents

are described by the linear, Ohmic scaling.

Considerable interest presents a consideration of small model systems with

arbitrary distribution of the individual GB misorientation angles or GB crit-

ical currents. Figure 10.21 shows an example, where the general grain align-

ment is determined to be very high (all GB angles < 3

◦

), with the existence

of two grains (A and B) with misalignment angles of 45

◦

. This conﬁguration

leads to a current distribution with the currents ﬂowing around the misaligned

grains.

When the current exceeds the critical current, the ﬁrst ﬂux line enters

the conductor along the misaligned grains (see Fig. 10.21b). The path of the

ﬁrst ﬂux line is also the limiting cross-section for the current ﬂow. In an

A similar approach is usually used in lattice analysis, approximating non-linear

transport properties [483, 844].

468 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

(a)

1.0

0.8 −

0.6 −

0.4 −

0.2 −

0.0

50 60 70 80 90 100

Current (A)

Voltage (μV)

−

A+B

Ref A

(b)

(c)

Fig. 10.21. (a) Hexagonal model lattice with GB angles between 2 and 3

◦

,except

for the grains A and B, having 45

◦

misorientation; (b) ﬂux distribution in the same

lattice; and (c) I–V characteristic for the same lattice, labeled “A + B.” Moreover,

the curves are shown with only one highly misaligned grain (A) and in the case of

no misaligned grains (Ref) [1188]

“undisturbed” lattice of the same topology, the limiting cross-section would

be nine GB segments across the conductor. In the case, presented here, the

limiting cross-section is reduced to six segments, if one disregards the GB

segments of the highly misoriented grains. Accordingly, one expects that the

critical current (i.e., the onset current, deﬁned here for non-zero voltage) is

decreased by a third.

The I–V curves in Fig. 10.21 show that indeed the critical current di-

minishes from 78 to 54 A, that is, by 32%. One can also see that the I–V

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 469

400

300

200

100

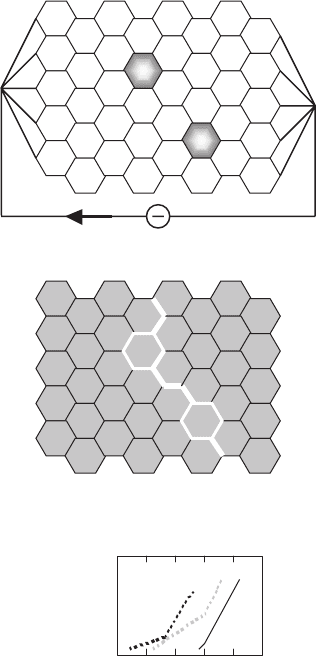
Percent of {001}<110> Grains

(kA /cm

)

% misoriented

grains

% fall in J

020

60 80 100

Fig. 10.22. Critical current on lattice of 25 × 50 hexagonal grains in dependence

of the percentage of grains with about 45

◦

misalignment

characteristics show pronounced kinking, similar to that found for low-angle

GB [430]. This kink indicates the onset of a new ﬂux channel through the con-

ductor or alternatively the branching of an existing channel. The eﬀect of the

misaligned grains on the value of I

is quite drastic: 5% of highly misaligned

grains (two grains from 40) lead to 32% reduction of the critical current. The

results of analogous simulation for the lattice with 25 × 50 hexagonal grains

are presented in Fig. 10.22 [1188]. In this case, the grain angles have been

assigned in a statistical manner, using two Gaussian distributions, centered

about 0 and 45

◦

, with their full-width half-maximum set at 5

◦

.Theyleadto

two practically separated percolative systems. The insert in Fig. 10.22 shows

that in this large system the critical current strongly decreases even at a small

percentage of misaligned grains.

Thus, the I–V characteristics in large lattice obey a parameter-independent

scaling law typical for percolative processes. In small aggregates, one can ﬁnd

piece-wise linear I–V curves, kinked at a point where new ﬂux channels enter

the conductor or existing channels branch out. In this case, highly misoriented

grains have a strong detrimental eﬀect on the critical currents.

10.5.3 Modeling of Electromagnetic Properties

of BSCCO/Ag Tapes

Based on the actual microstructure of BSCCO/Ag tape, in [833] the supercon-

ducting core is modeled as a stack of relatively well-aligned plate-like grains

whose ab-planes are approximately parallel to the magnetic ﬁeld, taking into

account the limiting of the intergrain current ﬂow by c-axis transport through

large-area twist boundaries [104], or by a lattice of low-angle “railway switch”

connections [150, 411], or by some other factors. The principal consequence

of the planar geometry is the current forcing in the direction perpendicular

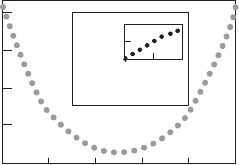
to magnetic ﬁeld H (see Fig. 10.23). In this case, the magnetization currents

tend to ﬂow in a plane perpendicular to H

(ﬁeld parallel to the one of the

major axis of the slab and plate-like grains), such that the distribution J(r)

is eﬀectively two-dimensional, and H(r) has only one component H

(x, y).

470 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

Fig. 10.23. Geometry of sample and magneto-optical indicator ﬁlm (1). Sketched

also are the model grain structure of BSCCO core of the “brick wall” type (2),

covered by silver sheath (3). The current streamlines are shown by thick arrows for

this planar geometry [833]

Consider the plate-like grain structure, presented in Fig. 10.23, ﬁrst ne-

glecting the non-superconducting second-phase precipitates and Ag/BSCCO

interface irregularities. For the ﬁeld orientation, shown in Fig. 10.23, the mag-

netization currents ﬂow macroscopically along the tape, but they must also

cross the ab-planes at some point in order to permit the current to loop at the

end of the tape and to create ﬂow around local barriers. In any case, the in-

tergrain current mostly ﬂows in the plane perpendicular to H, either through

the large-area GBs normal to the c-axis or through small-area low-angle GBs,

which separate slightly misoriented ab-planes (Fig. 10.23). In this case, the

two components J

(x, y)andJ

(x, y) are related to H

(x, y)as

(x, y)=

∂H

∂y

; J

(x, y)=−

∂H

∂x

. (10.33)

The local J

(x, y) values are found as J

=(J

+ J

)

1/2

, which yields

(x, y)=



∂H

∂x





∂H

∂y



. (10.34)

Therefore, for the speciﬁc geometry of magneto-optical (MO) measure-

ments, the current distribution is eﬀectively two-dimensional, permitting a

reconstruction of J(x, y) from a real measurement of the H

(x, y) distribution.

10.5 Current Percolation and Pinning of Magnetic Flux in HTSC 471

The characteristic spatial scales on which the above two-dimensional

scheme can be applied need some discussion. Obviously, second-phase pre-

cipitates, intergrowths, cracks, weakly coupled grains and irregularities of the

Ag/BSCCO interface can all lead to signiﬁcant deviations of the local J(r)

from the average current direction (the vector J(r)), generally having both

perpendicular (J

⊥

) and parallel (J

) components with respect to the local

direction of H(r). As a result, the ﬁeld H(r) can acquire a tangential compo-

nent, becoming dependent on z-coordinate, a feature, which is not taken into

account by the two-dimensional model. The characteristic size of L of these

inhomogeneities is estimated by the secondary phase and grain sizes. So, these

three-dimensional localized ﬁeld disturbances strongly decay over a distance

larger than L. However, if it is necessary to study the current distribution

over macroscopic scale (for l>L), the MO image can be averaged over the

length of L. After such averaging, any information about current loops smaller

than L and random tangential ﬂuctuations of H(r) will be lost. At the same

time, the macroscopic inhomogeneities of J(r) over spatial scales larger than

L can be extracted from the MO images, using the two- dimensional (10.33)

and (10.34).

Then, it may be supposed that the transport critical current density (J

)in

the Bi-2223/Ag tapes is limited by weak links at GBs. As it has been noted, su-

percurrent usually demonstrates two-dimensional behavior. At a grain bound-

ary, weak link breaks from superconducting to non-superconducting state

when current density and/or applied magnetic ﬁeld are suﬃciently high. An

electric ﬁeld is generated locally when all weak links break at a whole cross-

section of the column perpendicular to the current ﬂow axis. This behavior

can be treated as percolation phenomena based on the stochastic treatment.

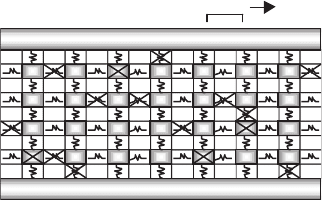
For simplicity, consider a single grain as an element in the system in which

grains are linked by GBs. Each element has coordination number Z deﬁned

by adjacent grains. As it is shown in Fig. 10.24, the system consists of M

elements in each column and N elements in each row (here Z = 4) [784]. The

stochastic computational procedure includes the following stages:

W = 1/8

= 4, N = 7, V = 24 /28, P = 55/67, C = 2

Fig. 10.24. System consisting of M elements in the column and N ones in the row.

Each element is connected by weak links with coordination number Z =4

472 10 Modeling of Electromagnetic and Superconducting Properties of HTSC

(1) Among the basic elements there select V % in superconducting state and

(100 − V )% in non-superconducting state. All elements are connected by

weak links.

(2) When the applied current to the system increases, the breaking of P %

weak links occurs (the broken links are selected randomly in the system)

and they transit in normal state when the current density, crossing weak

links, exceeds a critical value, J

(3) Supercurrents cross preferentially the superconducting links. When a

suﬃciently great number of weak links break, all links, included in a

column, are in non-superconducting state. When the current crosses this

normal column, an electrical ﬁeld is generated. The failure of P %from

total weak links leads to transition in normal state of W % columns from

total number.

(4) In order to consider the eﬀects of grain size, connectivity among grains,

etc., a parameter C is introduced, deﬁning the minimum size of elements

for keeping of superconducting state.

(5) Assuming Weibull’s distribution for estimation of strength of the weak

links, the probability P , by which the weak links break, is expressed as a

function of current density, crossing the respective weak link:

P = k(J − J

min

)

, (10.35)

where m is the distribution shape factor. Hence, we have:

J = J

min

+(P/k)

1/m

. (10.36)

For simplicity, it is assumed that J

min

=0.

(6) The fraction W of broken columns can be expressed through Weibull’s

function f(J

)as

W (J)=



f(J

)dJ

. (10.37)

On the other hand, the derivative of electric ﬁeld is given as

= R



f(J

)dJ

, (10.38)

where R

is the resistance for the uniform ﬂux ﬂow. Integrating W (J)with

respect to J, the electric ﬁeld is expressed as

E = R



W (J)dJ. (10.39)

Hence, a correlation of the parameters (P, W ) with the macroscopic quantities

(J, E) is followed.