Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

422 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

by the one-axially aligned reinforcing ﬁbers [267, 667, 1058]. The use of buﬀer

layers in the HTSC JJs is connected, in particular with attempts to signiﬁ-

cantly decrease the thermal and lattice mismatches. Therefore, an absence of

residual stresses will be assumed below. In this case, the damage processes

are caused by external tensile stresses (σ

∞

) remotely applied and parallel to

the ﬁbers (or analogously modeled buﬀer layers).

First, note some general features connected with the above fracture mech-

anism. The main idea of the toughening of the brittle matrix (including, in

the HTSC composites) by the brittle ﬁbers is linked with the processes of

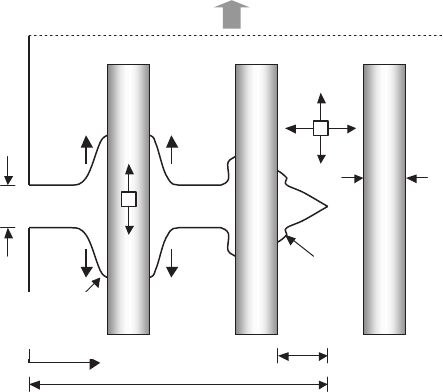
de-bonding and sliding at the interfaces (see Fig. 9.13). A de-bonding at the

matrix–ﬁber interface should be more favorable compared with a ﬁber frac-

ture at the matrix crack front in the case of the crack, inhibited by the ﬁbers.

The de-bonding is more probable than the ﬁber fracture, if the interface frac-

ture energy is suﬃciently small as compared with the ﬁber fracture energy.

Then, the HTSC composite, which to be under the de-bonding conditions,

demonstrates pushing eﬀect of the broken ﬁbers by the crack surfaces. At

the same time, an alternative fracture mechanism causes a growth of the ma-

trix crack through the ﬁbers without a de-bonding. So, a non-catastrophic

fracture mode could be obtained in the composites with weak interfaces and

high-strength ﬁbers (or buﬀer layers). For this sub-critical fracture mode, the

numerous matrix damages prior to a failure of the ﬁbers are proper. Then, the

complete strength of the composite is caused by the fracture of the ﬁbers and

by the following processes of the broken ﬁber pushing. The catastrophic mode

is found by the ﬁber fracture in the wake of the main matrix crack during its

Crack2u

∞

De-bonding

at Crack

Front

Sliding

De-bonding

in Wake

Zone

Fig. 9.13. Schematic representation of transversal matrix crack in layer HTSC

composite

9.4 Transversal Fracture 423

advancing. In this case, the complete strength is limited by the single dom-

inant crack and is found by a fracture resistance curve (i.e., dependence of

toughness on crack size) [267]. Then, a sliding of the broken ﬁbers or thin

buﬀer layers inevitably introduces a ﬁber pushing by the crack surfaces. This

process demands the study of ﬁber strength statistics, which is usually found

by Weibull’s distribution with the shape and scaling parameters m and S

,re-

spectively [1058]. A decrease of m corresponds to the more broad distribution

of the ﬁber strength, that is, to the fracture of greater number of the ﬁbers

far from the matrix crack front. This deﬁnes an increase of the ﬁber pushing

zone size. High median ﬁber strength is another useful property with a view

of the fracture resistance growth. It is found by the large values of S

,and

causes the sub-critical fracture mode.

For diﬀerent applications of HTSC JJs, it is more interesting to consider

a short crack, that is, the case, when the entire crack contributes in a stress

concentration, and a stress required for the crack growth is sensitive to its size.

Moreover, it is important to estimate critical parameters at the transition to

the steady-state cracking (i.e., to long crack), when the stresses at the crack tip

grow with an applied tension but are independent on the whole crack size. The

eﬀects of buﬀer layers on fracture of theHTSCcompositecanbeestimated,

introducing as the stresses, which close the crack surfaces, the stresses in the

buﬀer layers, playing role of the bridges between the crack surfaces [667]. The

corresponding decrease of SIF at the crack tip is calculated from these surface

attractions, using standard Green’s function. The crack growth criterion is

found, equating the SIF at the crack tip to intrinsic toughness of the matrix

without reinforcements (K

). Then an analysis of the buﬀer layer pushing

from the matrix, based on the results of [667], enables to ﬁnd a relationship

between the closure pressure (p)andthecrackopening(u)as

p =[uτV

(1 + η)/R]

1/2

, (9.16)

where η = E

;2R is the buﬀer layer thickness; τ is the sliding

frictional stress at the interface; E

and E

correspond to Young’s modules

of the matrix and buﬀer layer; and V

=1−V

isthevolumefractionofthe

matrix.

An approximate analytical solution for the short crack can be obtained,

assuming that the crack proﬁle at small crack sizes (c) does not diﬀer greatly

from that of the crack, subjected to uniform pressure. Then the crack opening

is found as [667]

u(x)=2(1− ν

1/2

(1 − x

)

1/2

, (9.17)

with the limiting displacement (2u

) and the equilibrium stress (σ

∞

) deﬁned

depending on the crack size, respectively, as

= σ

∞

R/τV

(1 + η) ; (9.18)

∞

/σ

=(1/3)(c/c

)

−1/2

+(2/3)(c/c

)

1/4

,c≤ c

, (9.19)

424 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

where E

= E

+ E

; ν

= ν

+ ν

;andK

= K

and

, referring to the SIF of the composite and of the matrix, respectively.

The crack size (c = c

), being transitional to the steady-state crack, and

the corresponding equilibrium stress (σ

∞

= σ

), which is independent on the

crack size, can be obtained as

=2[K

(1 + η)R/I

τV

(1 − ν

)]

2/3

; (9.20)

=(6.7/Ω)[I

(1 − ν

)(K

)

τE

(1 + η)

1/3

; (9.21)

for straight crack:

/σ

=1.02 ; c

=1.88 ; Ω = π

1/2

; I =1.20 ; (9.22)

for penny-shaped crack:

= σ

; c

= c

; Ω =2/π

1/2

; I =2/3 . (9.23)

Then, the steady-state toughness increment is found as [897]

ΔG



p(u)du, (9.24)

and we have, taking into account (9.16),

ΔG

=(4/3)α

3/2

, (9.25)

where α

=[τV

(1 + η)/R]

1/2

. Limiting by the case of the penny-shaped

crack and substituting σ

∞

= σ

into (9.18), we have ﬁnally:

ΔG

=4σ

/3α

. (9.26)

On the other hand, inserting the buﬀer layer strength (S) into (9.16) and

(9.24), found may be another equation for ΔG

[267]. Application of the spe-

ciﬁc dependence of ΔG

(on the parameter u

or S) is very important in order

to experimentally determine the value of ΔG

, namely to select the strength

test type, the shape and sizes of experimental sample. Then note that (9.20),

(9.21) and (9.26) include considerable number of material parameters; there-

fore, it is necessary to solve the problem of multi-parametric optimization for

their optimum selection with account of the speciﬁc loading conditions and

possible damages.

9.5 HTSC Systems of S-N-S Type

HTSC JJs of S-N-S type include laminated compositions of the ceramic–

metal–ceramic kind. First, consider a pair of the edge cracks, growing symmet-

rically and parallel to the metallic buﬀer layer, dividing two half-inﬁnite brittle

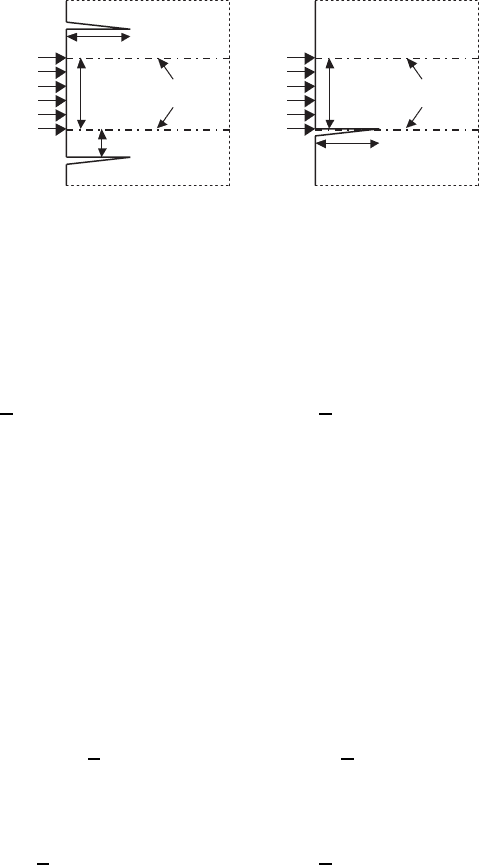
9.5 HTSC Systems of S-N-S Type 425

λ h

Interface h

Interfacepp

(a) (b)

Fig. 9.14. Model representations of damage in composites of the ceramic–metal–

ceramic type: (a) pair of steady-state cracks into brittle substrates and (b)interface

crack

half-planes (see Fig. 9.14a). Then, the SIFs determining the crack path may

be estimated using uniform pressure in the metal, p = E

(Δα

−Δα

/2)ΔT/

(1 − ν

), where Δα

= α

− α

and Δα

= α

− α

. The following are

analytical representations for the steady-state cracks and like ceramics [121]:

√

h = −0.26(1 + 2λ)

−1/2

; K

√

h =0.43(1 + 2λ)

−1/2

, (9.27)

where λh is the distance from the cracks to the corresponding interface and

h is the thickness of the metal layer. At the greater thermal expansion of the

metal, that is, for α

>α

(e.g., Ag), K

< 0, and edge cracks cannot grow

along interface, and only after coalescence near edge are able to propagate

into ceramic away from the interface. At smaller thermal expansion of the

metal, that is., for α

<α

(e.g., Mo), K

> 0 and a fracture along interface

is possible, when ductile layers are subjected to large residual stresses and has

a requisite thickness [447]. Therefore, the metals, which possess small thermal

expansion, are undesirable for bond integrity in HTSC JJs.

Inthecaseofsingleinterfacecrack(seeFig.9.14b),itmaybeshownfor

ceramic layers with like properties that the SIFs are maximal near the sample

edge. The equations for long crack (a ≥ 3h) are [121]

√

h = Φ

(h/a)

1/2

; K

√

h = ω(h/a)

1/2

, (9.28)

where Φ

≈±0.47 and ω ≈ 0.73, with negative sign of Φ

for α

>α

.The

values of the SIFs for short crack (a/h << 1) are given as

√

h = −0.99(a/h)

1/2

; K

√

h =0.63(a/h)

1/2

. (9.29)

The comparison of the solutions for single crack and pair of cracks deﬁnes

three diﬀerent regions, namely (i) the SIFs for both cases are equal at a<<h,

(ii) the SIFs for single crack have larger values at a<hdue to the shielding of

the crack pair and (iii) the SIFs for the crack pair exceed those for the single

crack at a>hbecause of full release of the strain energy in the metallic layer

by the crack pair.

426 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

In the case of unlike ceramics, the additive SIF, caused by the diﬀerence

in their properties, should be superimposed on the solution for like ceramics.

Obviously, this value is the SIF for body subject to the equal but opposite

surface forces on either side of the bond plane. The crack growth in the case of

small-scale yielding is found by the summary value of the SIFs from residual

and external stresses. We obtain K

> 0fortheedgecracksatα

<α

,and

the residual stress state will deﬁne the interface strength, S, corresponding to

maximum stress for the crack growth as [121]

S = E

/[2

√

π(Φ



+ ω

)ph(1 − ν

)] , (9.30)

where G

is the fracture resistance of the interface governed by the phase angle

of loading, Ψ ≈ π/6. Then, we obtain, K

< 0atα

>α

and the edge crack

growth is initially inhibited, but fracture nucleates from center. The interface

strength in this case can be given as [121]

S ≈ 0.5



πE

(1 − ν

) − p/10 , (9.31)

where G

is the fracture resistance governed by Ψ =0anda

is the radius of

the interfacial crack, which controls the fracture.

9.6 Toughening Mec hanisms

The toughening mechanisms in the S-N-S layered systems are connected with

the interface geometry, inducing the crack deﬂection and the out-of-plane

microcracking that constructs the links, bridges, which increase toughness

and fracture resistance at the stage of sub-critical crack growth along the

ceramic–metal interfaces. Microcracks–voids, formed during processing (e.g.,

using photo-lithographic techniques, combined with evaporation and diﬀu-

sion bonding) and localized at the ceramic–metal interfaces, under loading

promote the bridging bulges and stretching of the metal ﬁlm, which can in-

hibit the crack growth. In this case, a cracking both along plain side of the

patterned region and along the patterned side of the metal ﬁlm is possible.

As has been shown by the experiments conducted for glass–copper interfaces,

the toughness increase is nearly comparable for the samples, where the crack

is driven along the plain interface, wherein the crack deﬂection is absent, and

where the crack grows at the patterned interface, wherein the toughening re-

sults from both the crack deﬂection and bridging [778]. The R-curve behavior

(i.e., fracture resistance vs crack extension) states in the second case that

the crack bridging is the dominating mechanism for the crack tip shielding

(to compare with the crack deﬂection) in the interface toughening. The cor-

responding toughening mechanisms connected with the crack bridging and

deﬂection are shown in Fig. 9.15. The estimation of the toughening value in

the steady-state crack, induced by stretching of the metal layer, which re-

mains to be joined with the brittle substrate at one side (see Fig. 9.15a),

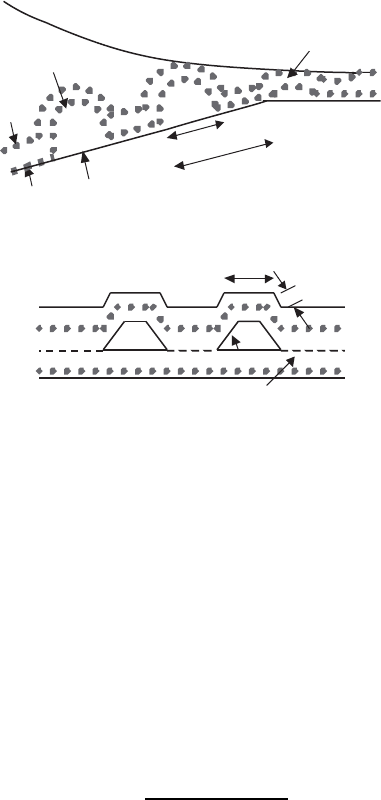
9.6 Toughening Mechanisms 427

Metal Film

Ceramic

(a)

(b)

Ceramic

Metal Film

Fig. 9.15. Two models of interfacial toughening due to (a) crack bridging under

plastic stretching of metal ﬁlm and (b) crack deﬂection

can be derived, assuming each metallic ligament stretches to the shape of arc

with height H,widthd and period λ. Then, the toughness increment (ΔG

)

is found through thickness h, yielding strength σ

and plastic strain ∈

for

metallic layer [778]:

ΔG

= σ

h ∈

= σ

h(8d/3λ)(H/d)

. (9.32)

The toughening in the case of the fracture along the patterned interfaces

due to the crack deﬂection can be estimated on the basis of the model for 2D

crack with repeated kink segments (see Fig. 9.15b) as [778]

ΔG

def

= G





D + d

D cos

(θ/2) + d



− 1



, (9.33)

where G

is the intrinsic toughness, taking into account the inclined and ﬂat

interfaces; D and d are the deﬂected and undeﬂected crack segment lengths,

respectively, and θ is the angle of the crack deﬂection. Finally, it should be

noted that a modest eﬀect of the toughening (compared to the macroscopic

crack deﬂection) occurs from much ﬁner scale surface roughness, causing both

the interfacial crack tilts and twists, which inhibit the crack extension and

induce greater the plastic stretching of the bridging metal ligaments as the

main crack extends [778].

428 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

Table 9.2. Material parameters used in calculations

Property YBCO SrTiO

Ag Mo

α(10

−6

−1

) 16.0 9.4 8.3 18.9 5.3

E(GPa) 64 300 380 75 315

ν 0.22 0.23 0.25 0.37 0.31

(MPa) – – – 25 570

Table 9.3. Numerical results

Composition h

/h K

/σh

1/2

∈

S(MPa) ΔG

ΔG

def

YBCO/SrTiO

4.9 – 1.41 – – –

YBCO/Al

0.8 – 1.60 – – –

YBCO/Ag – 1.38 – – – –

YBCO/Mo – 1.28 – – – –

YBCO/Ag/SrTiO

– – – 585 0.02 0.02

YBCO/Mo/SrTiO

– – – 380 0.51 0.02

The known material parameters (see Table 9.2) enable to estimate some

numerical results (see Table 9.3) for composite structures, which are proper

for HTSC JJs. We use in the computations the following relationships for

geometrical parameters: d/λ =2/3,H/d =0.1,D/d =0.15, and values of

θ =35

◦

= G

=2J/m

[778], K

=1MPa· m

1/2

,a = a

=3h =

300 nm, ΔT = 800 K.

9.7 Charts of Material Properties and Fracture

The numerical results may also be obtained for diﬀerent HTSC composites

of the S-I-S type using (9.1)–(9.3), (9.20), (9.21) and (9.26). However, even

initially, there are great spreads of the values for various mechanical and

strength properties, which caused the actual structure of these materials.

In particular, the elastic modules for HTSC ceramics can be 1–2 order of

magnitude smaller than the modules of the same superconducting crystals. For

example, in the case of BSCCO, the fracture toughness (K

) changes in the

range 0.5–3.0MPa ·m

1/2

, but Young’s modulus lies in the limit 54.1–230GPa

[775]. Therefore, the computations based on (8.20), (8.21) and (8.26) lead

to signiﬁcant diﬀerences for the limit values of K

and E

at other ﬁxed

parameters (see Table 9.4). These results are obtained in the simplest case,

considering two matrix layers (BSCCO) and one buﬀer layer (MgO) with the

same thickness (i.e., V

= 2), selecting other parameters as ν

=0.2 [648],

The same statement relates also to materials used in HTSC JJs of the S-N-S type,

some properties of which are presented in Tables 9.2 and 9.3

9.7 Charts of Material Properties and Fracture 429

Table 9.4. Some numerical results for penny-shaped crack

Properties c

(τ/R)

2/3

(R/τ)

1/3

ΔG

(R/u

τ)

1/2

=0.5MPa· m

1/2

; E

=54.1 GPa 3.516 6.408 14.507

=0.5MPa· m

1/2

; E

= 230 GPa 5.362 2.298 9.655

=3.0MPa· m

1/2

; E

=54.1 GPa 11.608 21.158 14.507

=3.0MPa· m

1/2

; E

= 230 GPa 17.704 7.588 9.655

=0.36,E

= 290 GPa [47]. The corresponding shear modules are found as

= E

/(ν

+1), wherek =1, 2. This example is also interesting from the

view of the HTSC processing due to the very small chemical reaction between

MgO and BSCCO melt [762].

The numerical results lead to qualitative trends in change of some nor-

malized parameters depending on the fracture toughness (K

) and Young’s

modulus (E

). For example, for the penny-shaped crack into superconduct-

ing matrix (see Table 9.4), the crack size, corresponding to its transition to

the steady-state crack (c

= c

), grows together with the fracture toughness

or/and Young’s modulus. In this case, the equilibrium stress (σ

= σ

)en-

hances with K

but diminishes with increase of E

. The fracture toughness

increment for the steady-state crack (ΔG

) decreases with increase of E

The normalizing multiples in the considered dependencies include tangential

stress at the interface, taking into account the sliding friction (τ) and the limit

displacement at the crack opening (2u

). These parameters state the features

of transversal fracture and characterize the material interfaces (in particular,

the de-bonding processes), and therefore, preliminary experimental deﬁnition

of these is necessary.

Similar spreads of data exist for YBCO and other ceramics and metals used

in HTSC JJs processing. The main causes, which ﬁnd these broad ranges of

material properties, are the following ones: porosity, microcracks, damages,

domain and crystallographic structures, etc. The eﬀects of porosity and mi-

crocracking on elastic modules of YBCO and BSCCO ceramics may be taken

into account, in particular, using the self-consistent diﬀerential method [577,

814]. In any case, mechanical properties every time should be selected with

account of speciﬁc microstructure, loading and fracture features of materials.

So, it is necessary to optimize elastic modules of both material components

in the estimation of Dunders parameter α, deﬁned in (9.3).

Anumberof

parameters are necessary to be given in the estimation of critical properties

of the HTSC-layered composites using (9.20), (9.21) and (9.26).

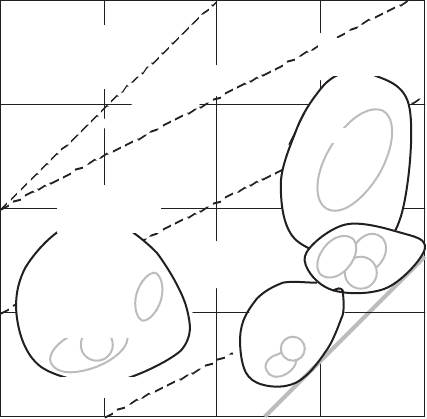
In order to solve the above selection problem, the material property charts

[30] may be useful. Figure 9.16 presents that chart, in which one property is

The parameter α, in particular, is very important in the estimation of the frac-

ture character, because its increase diminishes the fracture of interface cracking

to compare with the substrate failure in the plot of dependence of the relative

toughness (Γ

/Γ

) on the phase angle of loading (Ψ) [263]

430 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

1000

100

1.0

0.1

Threshold

Value

Directing Line

/E = C

=1000 (kJ/m

)

0.01

Engineering

Polymers

PMMA

Engineering

Ceramics

BSCCO

YBCO

MgO

ZrO

Glasses

SiO

0.1 1.0 10

Youn

’s Modulus E (GPa)

Fracture Toughess, K

(MPa·m

1/2

)

1000100

Epoxies

Polyethers

Metals

Engineering

Alloys

Fig. 9.16. Material property chart, representing K

vs E on logarithmic scales. The

guide lines K

/E = const help in fracture design of materials. Additional property,

= K

/E,isshown

plotted against another on logarithmic scales. This displays properties in very

clear form and ensures to represent additional fundamental relationships in

each chart (in particular, the critical release rate of strain energy, G

/E, is shown additionally in Fig. 9.16). These charts help to select range

for any property and to state criteria for the estimation of threshold material

behavior that are used in HTSC JJs processing, taking into account speciﬁc

loading conditions, thermal and electromagnetic treatments and so on.

When the crack grows through polycrystalline or composite structure,

a signiﬁcant change of the surrounding material characteristics occurs with

increase of the crack size and local stresses at the crack front. Numerous

toughening mechanisms are initiated, namely microcracking and twinning

near crack, crack branching and bridging, phase transformations and domain

re-orientations, interaction of crack with microcracks and mesostructure el-

ements, etc. Due to these, it is complicated to obtain the quantitative es-

timations of crack growth rate and hence to deﬁne a time before fracture

or sample durability for given stress (σ) and temperature (T ). Thus, it is

very diﬃcult to distinguish between action of various mechanisms of fracture

resistance and also material failure features. The fracture charts, based on

experimental data and plotted for many materials, solve this problem in some

way and help to select material properties, taking into account the fracture

9.7 Charts of Material Properties and Fracture 431

type. The boundaries in the fracture charts deﬁne equal contributions of adja-

cent regions, which correspond to action of speciﬁc fracture mechanism. They

displace at alteration of microstructure characteristics of the given material.

The fracture charts for b. c. c. metals (e.g., Mo) and f. c. c. metals (e.g., Ag)

diﬀer signiﬁcantly (see Fig. 9.17a and b). F. c. c. metals demonstrate only

–1

−6

−5

−4

−3

−2

σ /E

T, °C

σ (MPa)

0 0.2 0.4 0.6 0.8 1.0

–200

0.1

(b)

8006004002000

T/T

0.2 0.4 0.6 0.8 1.0

T/T

–1

−6

−5

−4

−3

−2

σ /E

0 T, °C

σ (MPa)

(a)

200016001200800400

Fig. 9.17. Fracture charts for Mo (a)andAg(b). Numbers denote the next fracture

types: (1) cleavage I; (2) cleavage II; (3) cleavage III; (4) dynamic fracture; (5) ductile

fracture; (6) transgranular and (7) intergranular creep fracture; (8) rupture. Dashed

curves show limit changes of interfaces