Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

412 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

(b)

(c)

BSCCO

MgO

100μm

(a)

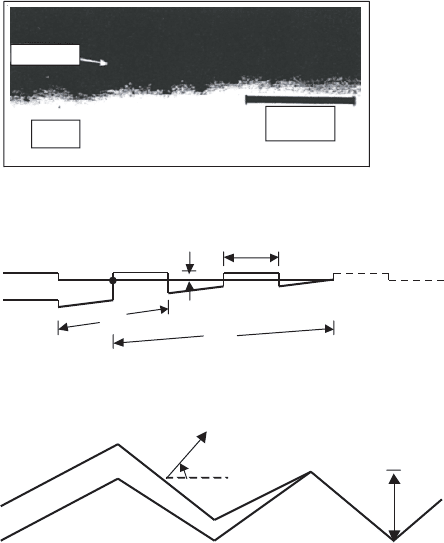
Fig. 9.4. (a) Proper interface between melted Bi-2212 thick ﬁlm and polycrystalline

MgO substrate (optical micrograph of cross-section [762]); and two models (b)and

crack (1), last contact point (2), crack tip (3) and interface (4)

where a is the crack size. Then, the condition of facet contact in the second

model [482] coincides with the condition of a single crack deﬂection in the

ﬁrst model [266]. In the case of existence of the facet contacts, the second

model as compared with the ﬁrst one takes into account, additionally, an

interaction between various crack deﬂections. The proper dependencies of the

crack shielding (ΔG/G), caused by the interface roughness, on the phase

angle of loading (Ψ) and on the diﬀerent inclinations of the facet sides (δ)

are shown in Fig. 9.5. The obtained trends of the crack shielding growth with

the phase angle of loading agree well with experimental observations of the

interface crack in diﬀerent ceramics, in which the steady-state crack trajectory

is caused by the condition, K

= 0 [263, 266, 482, 816].

9.2 Thin Films on Substrates 413

1.0

−

0.8

−

0.6

−

0.4

−

0.2

−

0.0

Phase Angle of Loading, Ψ

δ = 0°

20°

40°

60°

Crack Shielding, ΔG/G

0° 15° 30° 45° 60° 75° 90°

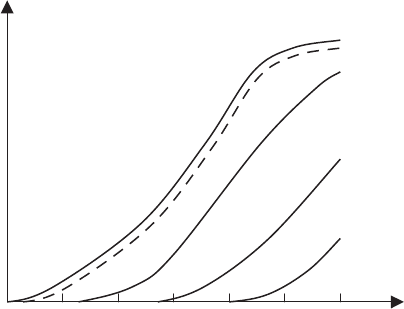
Fig. 9.5. Crack shielding (ΔG/G) vs phase angle of loading (Ψ). The dashed curve

corresponds to the model of contact zone (χ ≈ 100), and the solid curves are ob-

tained due to the model for diﬀerent inclination (δ)offacetsides

9.2 Thin Films on Substrates

During processing of JJ, the residual stresses can initiate in thin ﬁlms adherent

to substrates due to the deformation mismatches or/and thermal expansion

anisotropy. The residual stresses in YBCO ﬁlm structures, caused by diﬀerent

causes (e.g., lattice mismatches, thermal expansion, non-stoichiometry) can

reach, in whole, the value of ∼100 MPa [333]. A relaxation of these stresses

can also lead to the formation of defect structures, in particular the dislo-

cation mismatches form gradually with increase of the ﬁlm thickness and

accumulation of elastic stresses. Due to the high anisotropy of microstructure

properties, thin ﬁlms are subjected to the microcracking and twinning in the

speciﬁc directions. For example, generally, the cracks form into (001) plane,

and spacing between them increases with the ﬁlm thickness. First, crack oc-

curs in the ﬁlm at attainment of the critical thickness (H

), depending on

thermo-elastic stress of the lattice disagreement (σ) and fracture toughness

)asH

∼ (K

/σ)

[634]. The distinct feature of ﬁlm from bulk crystals is

a cellular domain structure inside single grains with the cell boundaries par-

allel to the (100) and (010) planes. The cells diﬀered by mutual replacement

of directions of the a-andb-axes and coupled coherently in similar to twins.

Together with external electric and magnetic ﬁelds, the internal stresses

lead to diﬀerent damage, developing in the ﬁlm-substrate system, in par-

ticular to the ﬁlm de-cohesion from substrate. The de-cohesion mechanism

depends on the residual stress sign (i.e., tension or compression) and exis-

tence of the stress gradient. In the ﬁlm tension, de-laminations initiate at the

414 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

sample edges and propagate into brittle substrate parallel to the interface

[221, 447]. Moreover, an across-ﬁlm cracking which nucleates at the free

surface is possible [446, 447], following its de-lamination and buckling [75].

Under conditions of compression, the ﬁlm de-lamination and buckling are

possible, too [75]. The investigations of mechanical and electromagnetic prop-

erties of HTSC ﬁlms are complicated due to (i) structure defects, (ii) high

anisotropy of elastic modules and (iii) existence of structure phase transfor-

mations [634].

In order to estimate strength parameters and study fracture features, the

composite beam theory is applied, assuming an existence of the initial mi-

crodefect crack at the sample edge. Consider the model sample, presented in

Fig. 9.6a, which is equivalent to the case of uniform distribution of the thermal

stress, σ

= E

ΔαΔT ,whereE

and ν

are elastic modules for the ﬁlm, Δα

is the diﬀerence of the thermal expansion factors between the ﬁlm and sub-

strate and, ΔT is the temperature diﬀerence, covered at cooling. Note that the

thermal strain, ε =ΔαΔT , must be replaced in the case of the deformation

h/2

Neutral Axis

Crack Trajectory

λh

Δh

Crack

λh

Neutral Axis

Film (E

, α

, ν

)

Substrate (E

, α

, ν

)

(a)

(b)

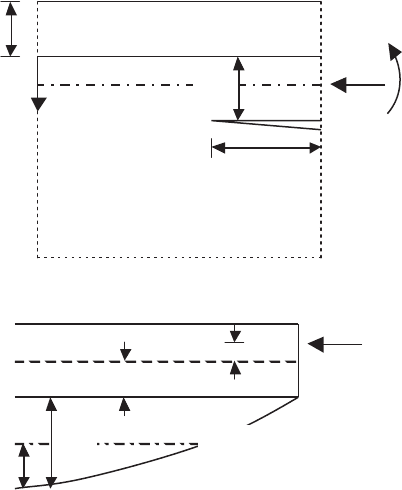
Fig. 9.6. Models of steady-state crack into substrate, taking into account (a)

thermal expansion diﬀerence between ﬁlm and substrate and (b) existence of stress

gradient in the ﬁlm

9.2 Thin Films on Substrates 415

mismatches by the strain, depending on the crystallographic properties of the

system. Then, the corresponding SIFs can be found by [221]

=0.434Ph

−1/2

(Σ + λ)

−1/2

+0.558M (Ih

)

−1/2

; (9.6)

=0.558Ph

−1/2

(Σ + λ)

−1/2

− 0.434M (Ih

)

−1/2

, (9.7)

where h is the ﬁlm thickness, Σ = E

(in the plane stress case) and

Σ = E

(1 −ν

)/E

(1 −ν

) (in the plane strain case); E

and ν

are the elastic

modules for the substrate; I = {Σ[3(Δ −λ)

−3(Δ −λ)+1]+3Δλ(Δ − λ)+

}/3 is the dimensionless moment of inertia; Δ = (λ

+2Σλ + Σ)/

2(λ + Σ); λ = z/h; P = σ

h is the load; and M = σ

λ(λ +1)/2(Σ + λ)is

the bending moment (per unit thickness). The steady-state crack path into

brittle substrate parallel to the interface is found by the condition K

=0.

Then, equating the SIF of I Mode to the fracture toughness of the substrate

= K

), we obtain the critical layer thickness (h

), of which complete

fracture is inhibited, as

=0.755(Σ + λ

)(K

/σ

)

, (9.8)

where λ

is the relative depth, governing the steady-state crack path, for which

=0.

Consider also the case of the stress gradient, existing on the ﬁlm thickness

(see Fig. 9.6b). In this case, σ

is the mean stress in the ﬁlm and M =

P [(λ +0.5 −Δ)h + ξ], where ξ is the distance from the ﬁlm center to the force

action line in (9.7). Similar to the previous model the parameters h

and λ

are found depending on the value of ξ, that is, on the given stress gradient.

Further more, the simple equations can be obtained for toughness param-

eters in the case of small-scale yielding of the substrate under condition of

steady-state transversal cracking of the ﬁlm. In this case, the strain energy

release rate (G

) and corresponding SIF (K

) are found as [446]

/σ

h = πF(Σ); K

/σ

√

h =



πF(Σ) , (9.9)

where σ is the ﬁlm tension (residual or/and applied); thefunction of F (Σ)is

given in Table 9.1 [446] for various values of Σ = Σ

/Σ

. Then, the typical

de-laminations, occurring from the notch orthogonal to the tension direction,

are classiﬁed in Fig. 9.7a and, b. In the case (a), there is a de-lamination of

open type, which grows together with the longitudinal cracking of the ﬁlm. In

the case (b), the longitudinal cracks are absent. The de-lamination remains

Table 9.1. Function F (Σ) dependent on ratio of elastic modules, Σ

Σ 43211/21/3

F (Σ) 0.79 0.75 0.70 0.62 0.57 0.54

416 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

(a) (b)

(c)

(d)

(e) (f)

Fig. 9.7. Typical de-laminations in ﬁlm-substrate structure (see explanation in the

text) [75]

to be closed and “pocket-like,” and the buckling takes place due to Poisson’s

eﬀect under suﬃciently-high applied stress. The form of this de-lamination

can be approximated by ellipse with semi-axes a and b.

Generally, the ﬁlm de-lamination from the substrate and its buckling in

compression as well as under tension can be studied in the framework of the

stability theory in fracture mechanics with consideration of diﬀerent stages

for crack-shaped defects [75]. The typical de-laminations under compression

are shown in Fig. 9.7c–f. By suﬃciently-high compression, the de-lamination

opens and is accompanied by a buckling, which is similar to the cylindrical

beam-like bending (case (c)). Case (d) represents a close de-lamination in the

form of ellipse with semi-axes a and b. The so-called edge de-laminations are

9.3 Step-Edge Junctions 417

presented by cases (e) and (f) and can be approximated by half-ellipse. In case

(f), the secondary crack can be observed, which grows across the de-lamination

as a result of the de-lamination bending.

In the case of the beam approximation, the critical buckling strain, ∈

can be estimated for acting compressive stresses in the ﬁlm and substrate

(σ

and σ

, respectively) by [978]

∈



(1 − 2ν

)

(1 − ν

)

(3 − 4ν

)

12(1 − ν

)





−1

, (9.10)

where

12(1 − ν

)

Σ(3 − 4ν

)

; Σ =

(1 − ν

)

(1 − ν

)

. (9.11)

9.3 Step-Edge Junctions

The strength problems, related to above ones arise, considering an inclined in-

terface crack in the step-edge JJs and in the S-N-S edge junctions with ground

planes. It is known that the tapered edges of the base electrode with edge an-

gles, being lesser than 45

◦

, are important to avoid a grain boundary formation

in the counter-electrode [454]. On the other hand, the shallower edge angles

have revealed problems with a void formation on the edges below 15

◦

[455].

So, in order to optimize the strength and damage behavior of these HTS JJs,

it is useful to consider a crack problem, when the crack surfaces contact at the

kinks. In this case, the SIFs of I and II modes at the crack tip (i.e., K

and

) diﬀer from corresponding applied SIFs by the values, which depend on

the kink angle (β), the kink amplitude and Coulomb friction factor (μ)(see

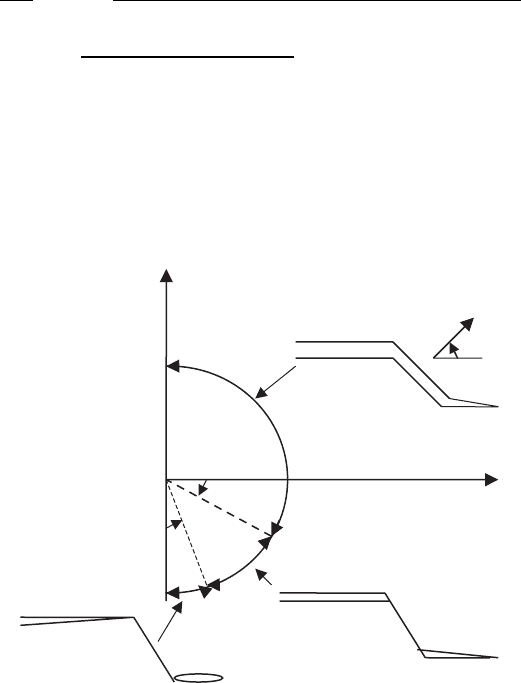
Fig. 9.8a). This geometry and a replacement of the inclined frictional force,

2∈d

(a)

2∈d

β − Φ

(b)

Fig. 9.8. Model of interface crack [266] in step-edge HTSC JJ used in order to

analyze eﬀects of the crack shielding

418 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

F , acting at the crack surfaces, by the homogeneously distributed tractions,

applied to the segment, 2 ∈ d (see Fig. 9.8b), enable to estimate a contact

eﬀect through normal and shear forces. In turn, it permits to determine the

contributions of this eﬀect on the SIFs at the crack tip and in the corre-

sponding displacements of the crack surfaces. Further more, it is possible to

consider the conditions of sliding and locking of the crack surfaces via terms of

the phase angle of loading (Ψ), the friction angle (Φ =arctanμ)andthekink

angle (β). An analysis, which has been carried out for K

> 0 [266], enables

to distinguish the main types of the crack behavior at the crack asperity (see

Fig. 9.9). Then, based on the conditions of a contact and a frictional locking,

the crack shielding (ΔG) may be estimated in the case of the sliding contact

due to the facet contact as [266]

ΔG

=2h(∈)

(sin β +cosβtgΨ)[sin(β − Φ)+cos(β − Φ)tgΨ]

cos Φ(1 + tg

Ψ)

−

(∈)(sin β +cosβtgΨ)

cos

Φ(1 + tg

Ψ)

, (9.12)

where 0 <β<π/2(forπ/2 <β<π, Φ must be replaced by (– Φ)), and due

to the crack locking as

ΔG/G =1− [1 − h(∈)]

, (9.13)

Φ−

Frictional

Locking

Sliding

Contact

Completely

Open Crack

Φ − β

(if > 0)

Fig. 9.9. Chart of possible crack behavior types, connected with crack asperity,

taking into account loading modes [266]

9.3 Step-Edge Junctions 419

where h(∈)=f(∈)/g(∈), but the functions f(∈)andg(∈) are found by

f(∈)=(

√

1+ ∈−

√

1−∈)/ ∈ ; (9.14)

g(∈)=

2 ∈



√

1+ ∈−

√

1−∈+



∈





√

1+ ∈ +1

√

1+ ∈−1



−



1 −

∈





√

1−∈

1 −

√

1−∈



. (9.15)

The comparison of h(∈) with the function, deﬁned from exact solution

of the problem on a microcrack ahead of a macrocrack [895], shows that the

proposed model slightly overestimates a crack shielding, caused by the facet

contact. The dependencies of the crack shielding (ΔG/G) on the various pa-

rameters for above two mechanisms are presented in Figs. 9.10 and 9.11. the

crack behavior due to the facet contact is more interesting. In the both ex-

amples of this case, namely without and with a friction (i.e., for Φ =0

◦

and

◦

, respectively), the crack shielding (ΔG/G) shows non-monotonous depen-

dencies on the phase angle of loading (Ψ). Initially, the value of ΔG/G grows

and then one diminishes with increase of Ψ. A friction presence displaces the

maximums of the curves in the direction of the increase of Ψ, restoring usual

tendency of a growth of the crack shielding with the phase angle of loading.

−

1.0

0.8

0.6

0.4

0.2

0.0

–0.2

–0.4

−

Phase Angle of Loading, Ψ

Crack Shielding, ΔG/G

β = 45°

60°

45°

75°

60°

75°

0° 90°75°60°45°30°15°

Fig. 9.10. Crack shielding (ΔG/G) as functions of phase angle of loading (Ψ ),

kink angle (β) and friction angle (Φ). Solid curves correspond to the case of friction

absence (Φ =0

◦

), and dashed curves ﬁnd the case of Φ =45

◦

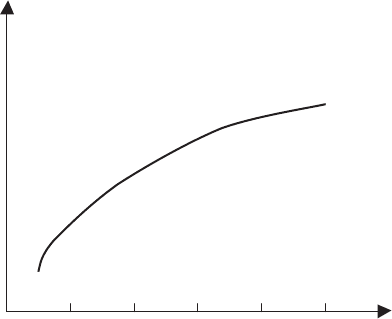
420 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

−

1.0

0.9

0.8

0.7

0.6

0.5

Crack Shielding, ΔG/G

0.0 0.2 0.4 0.6 0.8 1.0

∈

Fig. 9.11. Crack shielding (ΔG/G) vs parameter ∈ in sliding contact (eﬀect of the

crack locking)

At the same time, a displacement of the maximums in the direction of the

decrease of Ψ occurs, increasing the kink angle β. The latter corresponds to

diminution of the edge angle (α) of the step-edge junction, since α =90

◦

− β.

Further more, a non-zero friction may introduce the contrary mechanism to

the crack shielding, namely the crack ampliﬁcation (ΔG<0). This is impos-

sible in the case of 90

◦

<β<180

◦

,whenΔG/G grows monotonously with Ψ

(into interval of its alteration from 0

◦

up to 90

◦

) [266]. Thus, the crack, which

climbs on a step, is more safe as compared with the crack that goes down from

the step. Therefore, the maximum values of the crack shielding for the present

type of HTSC JJs may be found, thanks to an optimum and simultaneous se-

lection of the parameters β,Φ and Ψ in accordance with the trends, depicted

in Fig. 9.10. In the case of the crack locking, a monotonous growth of the

crack shielding takes place with the parameter ∈ (see Fig. 9.11), which ﬁnds

the step size at given values of β and d. The greater edge size corresponds to

the greater microcrack ahead of a macrocrack in the case of the inclined inter-

face, at β = const and at the invariable crack shielding. Then, even the small

structural defects (with a high probability initiated at the interfaces during

HTSC JJ processing, for example, due to the thermal anisotropy or/and crys-

tallographic mismatches) may be suﬃcient in order to achieve an actual crack

shielding, at the small edge size.

9.4 Transversal Fracture

During HTSC JJ processing and a device work under high electromagnetic

ﬁelds, a nucleation and a propagation of microcrack-like defects in the direc-

tion perpendicular to the layers of the HTSC composite is possible (e.g., see

9.4 Transversal Fracture 421

100 μm

(b)

Bi-2212

Crack

(a)

BSCCO

Transversal

Fracture

Fig. 9.12. (a) SEM micrograph of transversal fracture of BSCCO/Ag rod [775] and

(b) SEM image of cross-section of Bi-2212/Ag ﬁlm with transversal crack [275]

Fig. 9.12). On the whole, fracture picture and fracture resistance are not only

caused by the material properties and by the geometrical parameters of thick

(matrix) layers and thin (buﬀer) layers, but even rather by the failure features

at the interfaces. The de-cohesion (or de-bonding) processes at the material

interfaces may be caused by the residual stresses, formed during the HTSC

JJ processing. In this case, the internal stresses may be increased by the sup-

plementary stresses due to the thermal change and/or Lorentz forces. The

mechanical damage, nucleated by de-cohesion processes, causes an immediate

diminution of the functional properties of the junction, decreasing steadily

with time, that limits reliability and longevity of the device. At the same

time, a partial de-cohesion can play a positive role in the case of a transver-

sal fracture of the HTSC layer composite, increasing its fracture resistance.

Hence, it is necessary to estimate diﬀerent strength parameters and fracture

toughness, which should be obtained in the framework of fracture mechanics,

applied to the brittle matrix–ﬁber composites, when a matrix crack is bridged