Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

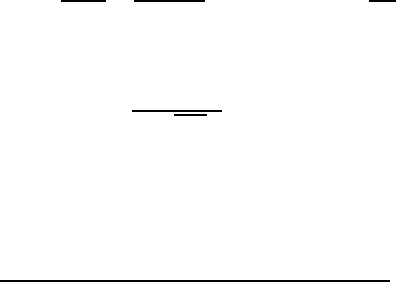
8.2 Twinning Processes in Ferroelastics and Ferroelectrics 381

fracture resistance, which are intrinsic for the material structure, and deﬁnes

essentially true strength properties. In the framework of the force approach

by using the SIF for given fracture mode (I, II, III or their combination), the

constitutive relationships, deﬁning equilibrium states of crack growth at the

pointed stages of its propagation, have the form [163]:

dK/dc>dK

/dc for unstable fracture ; (8.71)

dK/dc<dK

/dc for stable fracture , (8.72)

where c is the length of the growing crack; K

is the critical value of SIF,

deﬁning the crack start (i.e., the ceramic fracture toughness). If there are

internal mechanisms, contributing in the change of the crack growth, then

eﬀective driving force, acting in the crack tip (K), can be presented as a sum

of applied external load (K

) and internal residual stresses (K

K = K

. (8.73)

The terms of K

in (8.73) can interpret the shielding and anti-shielding

(leading to the crack ampliﬁcation) inﬂuences on transmission of external

stresses to the crack tip depending on their signs (i.e., negative or positive,

respectively). In particular, the microcracking near macrocrack, crack branch-

ing and crack bridging, studied in Sect. 7.1, lead to the shielding eﬀects. At

the same time, the microcrack–macrocrack coalescence causes a decreasing of

fracture resistance (the anti-shielding eﬀect).

Now, consider directly the toughening of HTSC ceramic, caused by the

processes of twinning near growing crack. In this case, the hydrostatic com-

ponent of stress, required to introduce the transformation, is obtained from

the condition ΔΦ ≤ 0 and can be written using (8.67) as

ΔV ≥−ΔF

6ΔΓ

ηd

(η

− 1)

+0.14EΔV

0.4

Gγ

. (8.74)

The hydrostatic stress near the crack tip is subjected to the non-equality

[261]:

≤

2K(1 + ν)

√

2πr

cos(Θ/2) , (8.75)

where {r, Θ} are the polar coordinates connected with the crack tip. Then,

using non-equalities (8.74) and (8.75), we obtain the distance of r

∗

from the

crack tip at which single grain will be subjected to the transformation. We

have for ν =0.2:

2πr

∗



0.8KΔVdη

cos(Θ/2)

[2(3ΔΓ

+0.2Gγ

d)ηη

− Γ

(η

+ η)](η

− η)

. (8.76)

Then, the size of the transformation zone, r

, can be calculated, using

(8.76) at K = K

and maximum value of the reached toughness (for Θ ≈ π/3)

382 8 Computer Simulation of HTSC Microstructure and Toughening

[262, 668]. The latter suggests that each particle is subjected to suﬃcient

shear stress, which introduces the martensitic transformation under condition

of thermodynamic limit (8.68) (at p

= 0), superimposed on the particle.

Note that the value of the angle Θ ≈ π/3 divides the zones of the toughening

and the crack ampliﬁcation near the crack tip. The transformed particles at

the crack front increase K

tip

(the stress concentration at the crack tip), while

the particles disposing into the region, |Θ| >π/3, lead to the opposite eﬀect.

Finally, consider the toughening, increasing fracture resistance of HTSC

ceramics due to twinning in the process zone with width 2r

, surrounding the

advancing crack (see Fig. 8.26). Taking into account the superconductor be-

havior, caused by the hysteresis curve “σ–ε”, we can estimate the toughening

for the steady-state crack, caused by the twinning as [102, 192]



)

+ EΔJ

, (8.77)

where ΔJ

(

U(y)dy is the increment of fracture resistance; U is the

square under the curve “σ–ε”,calculated at each value of y-coordinate on

(a)

1.0

0.5

0.0

π/3 2π/3 πθ

ΔK

|ΔK*|

(b)

Fig. 8.26. Eﬀect of transformation zone, forming near crack (1), on ceramic tough-

ening: (a) frontal (2) and wake (3) zones of toughening (the pointed parameters

are discussed in text); (b) fracture toughness change, connected with disposition

of transformed particle; ΔK is the SIF diﬀerence due to total development of the

transformation zone, that is, at great values of Δc/r

[262]

8.2 Twinning Processes in Ferroelastics and Ferroelectrics 383

the basis of the governing law for the material subject to the twinning.

Equation (8.77) is reduced to the following form for one-axis curve “σ–ε” [192]:



(E − H)



8π





−







1/2

, (8.78)

where K

is the fracture toughness of the superconductor for the steady-

state crack; K

=(2γ

1/2

is the ceramic toughness without the twinning

process; γ

is the fracture energy; H is the hardness factor of the ceramic

at indentation; σ

is the threshold stress, stating a transition to non-elastic

material behavior due to nucleation of the twinning near the crack tip.

In order to obtain numerical results, we use the known parameters for

YBa

7−x

,namely:G =41GPa,γ

∼ S

=0.018,Γ

∼ σ

=0.01 J/m

[261]. In more detail, we discuss a selection of the values for the volumetric

deformation, ΔV , and the threshold stress, σ

(∼ P

). As has been shown

in [344], the spontaneous (non-elastic) deformation initiates at temperature

= 920 K, resulting in the structural phase transition from tetragonal phase

(P 4/mmm) to orthorhombic (P mmm). This deformation is deﬁned by the

components C

and C

of the elastic stiﬀness matrix. Below the tem-

perature of T

(into orthorhombic phase), the formed domain structure of

HTSC can re-switch from one spontaneous deformed oriented state to the

other by external shear load, σ. The shear modulus attains minimum value

for σ = σ

(where σ

is the coercive stress), because the number of twins

is maximum in this case, and the sample is most compliant to mechanical

loading. The number of twins decreases at σ>σ

, leading to greater stiﬀness

of the sample and to increasing of G. Due to this, we select as the thresh-

old value the next one: σ

= σ

. The presented temperature dependencies of

[344] in the vicinity of the phase transition give the value of σ

≈ 3MPa.

This is much less than the corresponding value of the threshold stress, causing

the twinning (20 MPa) that is calculated in [578] for BaTiO

samples, tested

on impact load at diﬀerent rates of the loading, and also than the value for

partially stabilized ZrO

(4 GPa) [863]. Finally, the spontaneous deformation

jump at the phase transition, we suggest, is equal to ΔV =10

−4

, according

to experimental results of [344]. This is also much less than the corresponding

values for BaTiO

(54 × 10

−4

) [849] and for ZrO

(57 × 10

−3

) [863].

Substitute the necessary values in (8.68) (at p

= 0), calculating the

preliminary values of the twin extent, d, from (8.69) for the observed grain

sizes of YBCO, D = 10–100 μm. The solution (8.68) for the above range of

the grain sizes leads to the value of η

→ 0. Then, from (8.76) and (8.77)

an absence of real toughening for HTSC ceramics, caused by the twinning

processes, is found. This is explained by very small magnitudes of ΔV and

(∼ P

), deﬁning a spontaneous strain in the YBCO, compared to the cor-

responding values for partially stabilized ZrO

[863] and ferroelectric ceramic

BaTiO

[578, 849], where the twinning processes play the most important

rule in material toughening. Thus, the toughening (or crack ampliﬁcation)

384 8 Computer Simulation of HTSC Microstructure and Toughening

at the fracture of YBa

7−x

superconducting ceramic is caused by mi-

crocracking due to deformation or/and thermal anisotropy, and by the pro-

cesses, connected with microcracking (in particular crack branching and crack

bridging), but not transformations of the martensitic type.

8.3 Toughening Mechanisms for Large-Grain YBCO

8.3.1 Model Representations

Two main computer simulation approaches, namely Monte-Carlo simulations

[814, 821] and phase ﬁeld method [937, 956, 1016], are usually used to study

microstructure transformations, which accompany the YBCO fabrication. The

phase ﬁeld method has been discussed in Sect. 7.1.6. Here, we consider a modi-

ﬁed Monte-Carlo scheme. The simulation of the YBCO precursor microstruc-

ture will be based on the re-crystallization model for ferroelectric ceramics

[516, 823] and on the study of thermal conductivity in mixes and structure-

heterogeneous solids [234]. Formation of the ﬁnal YBCO microstructures, us-

ing seeds at existence of dispersed 211 phase, will be found by the Monte-Carlo

techniques [22, 1009, 1010].

A precursor microstructure after YBCO pellet modeling is represented by

discrete lattice with 2000 square cells of characteristic size δ. Each lattice cell

is assigned a number (between 1 and Q), corresponding to the orientation of

the grain in which one is embedded. All grains have diﬀerent orientations,

deﬁned during the pellet microstructure simulation, in which lesser numbers

correspond to earlier initiated crystallites. This liquidates a neighborhood of

the grain of the same orientation. Then, the cells which have neighbors with

unlike orientation lie at the grain boundary; in the other case, they are placed

in grains. The grain boundary energy is speciﬁed, deﬁning an interaction be-

tween nearest neighboring lattice sites as [22, 1009, 1010]

E = −J

(δ

− 1) , (8.79)

where S

is one of the Q orientations on site i(1 ≤ S

≤ Q),δ

is the

Kronecker’s delta. The sum is taken over all nearest neighbor sites (nn), J is

a positive constant that sets the energy scale of the simulation. Note that the

orientation dependence of the energy of a straight boundary segment exhibits

a ratio of the maximum to minimum boundary energy of 2/

√

3 for triangular

lattice and

√

2 for square one. Both ratios are close to unity, that is, the grain

boundary energy is nearly isotropic and only weakly lattice dependent [22].

In simulation of boundary motion kinetics by the Monte-Carlo techniques,

a lattice cell is selected at random, and a new trial orientation is randomly

changed to one of the other grainorientations. Then, the energy alteration

8.3 Toughening Mechanisms for Large-Grain YBCO 385

caused by change in orientation (ΔE) is evaluated. The transition probability

(P ) is given by [22]

P =



exp(−ΔE/k

T )ΔE>0

1ΔE ≤ 0 ,

(8.80)

where k

is Boltzmann constant, T is the temperature. A re-orientation of

a site at a grain boundary corresponds to boundary migration. A boundary

segment moves with rate, related to the local chemical potential diﬀerence

(ΔE

) as [22]

= C[1 − exp(−ΔE

T )] , (8.81)

where factor C is found by the boundary mobility and symmetry of the lattice.

The simulations for the cases of T ≈ 0andT ≈ T

,whereT

is the melting

point, have shown similar results [1009]; therefore, we use T ≈ 0, below.

The (N −N

) attempts of re-orientations, where N is the number of lattice

cells and N

is the total particle number, are arbitrarily used as unit of time

and deﬁned as one Monte-Carlo step (MCS) per site. In order to incorporate

particles of 211 phase into the model, corresponding cells are assigned by ori-

entation which are distinct from all grain orientations. It is suggested that

the particle concentration and sites initially arbitrarily selected are ﬁxed dur-

ing simulation and are independent from any attempts of cell re-orientation.

The insertion of the crystalline seed into microstructure is done by replacing

the grains at the center of the microstructure with one large square grain

with characteristic size considerably greater than the mean grain radius of

the YBCO precursor pellet.

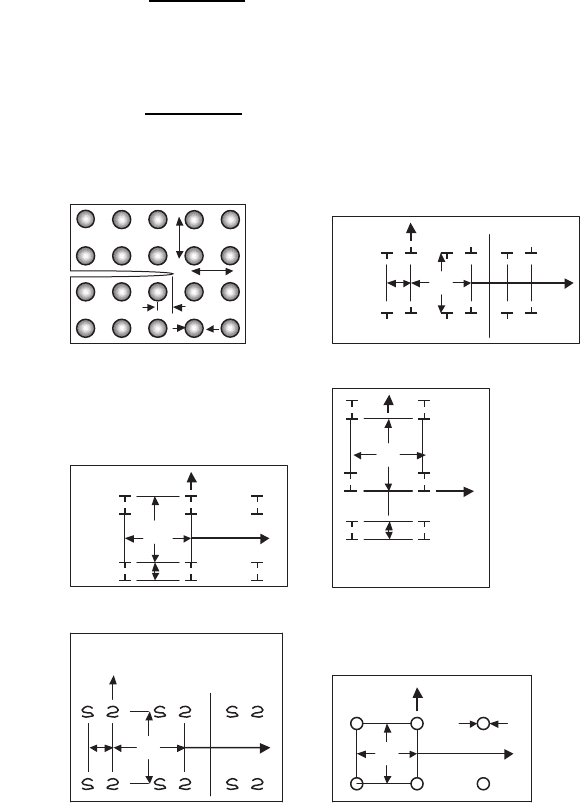
In the computer simulations, we consider three cases of YBCO microstruc-

ture evolution after primary re-crystallization (see Fig. 8.27):

(1) particle dispersion of 211 phase into matrix of 123 phase;

(2) insertion of large grain (seed) into matrix of 123 phase;

(3) insertion of large grain (seed) into matrix of 123 phase with dispersed 211

phase.

77 77

64 64

15 15 15

151515

31 31

23 23

3434

77 77 77 9027 27

64 64 64

6464

47 47

52 1

111

115

23 23

23 23 23

34 34

4848

777777

64 64

15 15 15

151515

15 15

31 31

(c)(a) (b)

23 23

34343

Fig. 8.27. Three models of YBCO microstructure evolution, used in computer

simulations: (a) dispersion of 211 phase (black) in 123 matrix, (b) large-grain seed

(white) in 123 grain matrix and (c) 211 dispersion and grain-seed in 123 matrix

386 8 Computer Simulation of HTSC Microstructure and Toughening

As a condition of the computation stop in the ﬁrst and third cases, an exis-

tence of one particle at any intergranular boundary at least (that corresponds

to complete pinning of microstructure with dispersed particles [1009, 1010]) is

selected. In the second case, the computations are ﬁnished when some grain

radius attains the seed grain size.

In order to obtain statistically representative results, we use approach

[145]. Then, using comparatively small grain aggregates together with stere-

ological method accelerates computations due to the operation with smaller

arrays of variables and obtains necessary statistics.

8.3.2 Eﬀect of 211 Particles on YBCO Fracture

As has been shown in the previous chapters, a special eﬀect on the 123 ma-

trix fracture may be exerted by dispersed inclusions of the 211 phase. The

platelet structure of 123 superconducting phase covering the 211 single inclu-

sions during solidiﬁcation from melting via a zipper-like mechanism promotes

the formation at the 123/211 phase interface of the defects-faults and increased

dislocation concentration. Therefore, the existence of secondary phase inclu-

sions causes the alteration of the strength properties indirectly and directly.

In the ﬁrst case, these inclusions inﬂuence formation of certain microstruc-

tures during material fabrication with corresponding fracture resistance. In

the second case, these inclusions deﬁne the acting toughening mechanisms,

fracture toughness and strain energy release rate. Therefore, we consider the

possible mechanisms of toughening in the case of the composite structure

YBa

7−x

BaCuO

(a)

(b)

Fig. 8.28. (a) Tilt and (b) twist of crack at its interaction with inclusion

8.3 Toughening Mechanisms for Large-Grain YBCO 387

Crack Deﬂection

As the 123/211 interface strength is less than YBCO matrix strength, a crack

deﬂection around dispersed particles (see Fig. 8.28) in the form of crack tilt

and twist is possible. Then the driving force of the crack, which orients ran-

domly to the main tension vector, is described by the local stress intensity

factors k

and k

, corresponding to the opening, sliding and tearing frac-

ture modes. The crack driving force, governed by the strain energy release

rate, G, is found as [268]

EG = k

(1 − ν

)+k

(1 − ν

)+k

(1 + ν) , (8.82)

where E and ν are the elastic modules.

In the case of applied SIF of mode I, K

,thelocalSIFsofk

(i =1, 2, 3)

for tilted crack are given as [268]

= F

(Θ)K

; k

= F

(Θ)K

, (8.83)

where

(Θ)=cos

(Θ/2) ; F

(Θ)=sin(Θ/2) cos

(Θ/2) . (8.84)

For twisted crack the local SIFs of k

are found by [268]

= F

(Φ)k

+ F

(Φ)k

; k

= F

(Φ)k

+ F

(Φ)k

, (8.85)

where

(Φ)=cos

(Θ/2)[2ν sin

Φ +cos

(Θ/2) cos

Φ];

(Φ)=sin

(Θ/2) cos

(Θ/2)[2ν sin

Φ +3cos

(Θ/2) cos

Φ];

(Φ)=cos

(Θ/2) sin Φ cos Φ[cos

(Θ/2) − 2ν];

(Φ)=sin

(Θ/2) cos

(Θ/2) sin Φ cos Φ[3 cos

(Θ/2) − 2ν] . (8.86)

The computation of toughening due to crack deﬂection is the statistical

problem, which is connected with averaging of the driving force in all possible

tilt and twist angles. The eﬀect of particle volume fraction, V

, which causes

an initial crack path alteration, is equal to [268]

=1+0.87V

, (8.87)

where G

and G

are the fracture toughness of composite and matrix, respec-

tively. The inclusions with higher characteristic ratio have stronger eﬀects,

that is, spherical particles create a lesser toughening compared with disk-

shaped and rod-shaped ones. Toughening eﬀect attains saturation at V

≈ 0.2.

An increased dimension of loading generally causes the increase of crack driv-

ing force due to the complexity of stress state and decrease of toughening

eﬀects.

388 8 Computer Simulation of HTSC Microstructure and Toughening

Crack Pinning by Particles

In the case of small-scale crack bridging in which the bridging zone size (L)is

small compared with the crack length, sample sizes and distance from crack

tip to the sample boundaries, the crack pinning by elastic particles with size

2a (see Fig. 8.29) is possible. Then, the toughening factor, Λ, may be found

as [101]

Λ ≡



ω(1 − c)



πS

ac(1 − c

1/2

)

1/2

; ω =

E(1 − ν

)

(1 − ν

)

; c =(a/b)

(8.88)

where K

and K

are the critical SIFs for crack growth in composite and in

matrix, respectively; S is the particle strength; b is the radius of penny-shaped

crack with central pinning particle; E and ν are eﬀective elastic modules of

composite (E

and ν

are the elastic matrix constants). Thus, the toughening

is increased with inclusion size and strength.

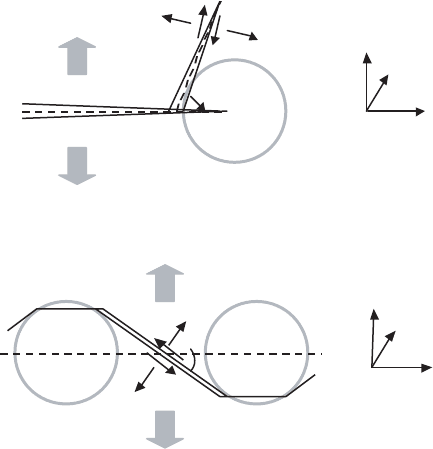
Toughening due to Periodically Distributed Inclusions

The internal stress state caused by periodically distributed inclusions is al-

most sinusoidal at the mean plains between inclusion layers, where a ﬁnite

crack is placed along the x-axis. Dislocation techniques have been applied to

Fig. 8.29. (a) Crack pinning by particles and (b) crack opening; ν is the crack

opening rate; σ

is the stress, loading the particle

8.3 Toughening Mechanisms for Large-Grain YBCO 389

inclusions, modeled by centers of shear, compression, anti-plane and extension

(dilatation) (see Fig. 8.30 [621]). These are the following results:

(1) For shear centers:

ΔK

=1.6

μV

1/2

(1 − ν)

; a<<λ; b

= he

. (8.89)

(2) For horizontal compression centers:

ΔK

=1.6

μV

1/2

(1 − ν)

; a<<λ; b

= he

. (8.90)

(d)

–σ

(b)

(f)

(e)

(c)

(a)

Fig. 8.30. (a) Crack toughening by periodical array of inclusions; dislocation struc-

tures (with Burgers vector, b), modeling the inclusions: (b)shearcenters;(c)hor-

izontal compression centers; (d) vertical compression centers; (e) anti-plane shear

centers and (f) extension (dilatation) centers

390 8 Computer Simulation of HTSC Microstructure and Toughening

(3) For vertical compression centers:

ΔK

=2.2

μV

1/2

(1 − ν)

; a<<λ; b

= he

. (8.91)

(4) For anti-plane shear centers:

ΔK

III

=0.4μV

1/2

; a<<λ; b

= he

. (8.92)

(5) For extension (dilatation) centers:

ΔK

=0.8

1/2

(1 − 2ν)

; a<<λ; e

=ΔV/V . (8.93)

Thus, the SIF diﬀerence of corresponding mode for periodically distributed

inclusions is proportional to the elastic modulus, volume fraction of the inclu-

sions, deformation mismatches (e

αβ

) and square root of the inclusion spacing

(λ). However, it is independent of the crack length, that is, the dispersion

toughening is more eﬀective at the crack initiation to compare with its growth.

8.3.3 Some Numerical Results

The numerical results presented in Table 8.7 [822] have been found for some

microstructure properties in all possible variants that are found by the 211

particle concentration (f =0.1 and 0.2) and the seed size (S

≈ 2S

and

,whereS

is the seed area and S

is the maximum grain square after

primary re-crystallization before beginning of the 123 grain growth). The ﬁnal

microstructures with the dispersed 211 particles demonstrate dependencies

similar to

S ≈ 4a/f,where

S is the mean pinned grain area, a is the particle

square. This corresponds to the topological ideas developed in the computer

simulations of the grain pinning by dispersed particles [1009]. The behavior of

outstripping grain growth around seed coincides well with the computational

results of large grain growth in the microstructure of normal grain growth

[1010] and the growth morphology of YBCO specimens with seed, solidiﬁed at

unfavorable temperatures [640]. Moreover, the present computer simulations

may be characteristic to the pushing process of the 211 particles due to 123

front advancing [640]. The numerical results show a correlation between the

grain area,

S, and superconducting ﬁeld per grain,

Table 8.7. Numerical results

Para-

meters

f =0.0,

≈ 2S

f =0.0,

≈ 3S

f =0.1,

≈ 2S

f =0.1,

≈ 3S

f =0.2,

≈ 2S

f =0.2,

≈ 3S

S/δ

13.89 23.81 45.45 50.03 62.50 25.01 29.41 31.25

/δ

13.89 23.81 40.91 45.08 56.25 20.05 23.53 25.00