Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

8.6 Toughening of Bi-2223 Bulk, Fabricated by Hot-Pressing Method 401

boundary energy and its mobility on grain misorientation, using a correspond-

ing texture component for each grain. For simplicity, we limit the texture

components to two (A and B), which are quite suﬃcient to describe consider-

able number of test data. In particular, we could model the growth processes

for considered anisotropic Bi-2223 superconductor along the c-direction and

in the ab-plane. Mass transfer between crystallites is based on the following

assumptions [245]:

(1) The migration rate of a boundary between two grains i and j is given by

= m

=2γ

(1/R

− 1/R

) , (8.116)

where p

is the driving force, m

and γ

are the mobility and boundary

energy, (1/R

− 1/R

) is the average curvature for this grain boundary

and M

=2m

is the grain growth diﬀusivity.

(2) All grains of the same size and orientation experience the same growth

rate (homogeneity condition).

(3) The grains, surrounding a given grain, are distributed randomly with re-

spect to size and orientation.

Then, the grain growth rate of the size class i with a texture component

A (or B) without the growth stagnation is found by [245]

A(B)

/dt = M

A(B)

∗

[1/R

A(B)

∗

− 1/R

A(B)

] , (8.117)

where M

A(B)

∗

and R

A(B)

∗

are the integrated diﬀusivity and integrated critical

radius, respectively, controlling the grain growth of the component A (or B).

Note that the value of R

A(B)

∗

is the intermediate grain size of the component

A (or B) between increasing and decreasing grains, and M

A(B)

∗

determines the

rate of these processes [245]:

∗

+ F

; M

∗

+ F

;

(8.118)

∗

+ F

R

 + F

R



; R

∗

+ F

R

 + F

R



(8.119)

where M

(H, K = A or B) is the grain-growth diﬀusivity of a boundary

between grains of the orientation classes H and K. The grain fraction of the

size class i with the orientation A (or B) is deﬁned as

A(B)

= n

A(B)

;

i=1

+ n

)=N

;

i=1

+ F

)=1; F

A(B)

i=1

A(B)

(8.120)

where N

and N

are the total number of size classes and grains, respectively;

A(B)

is the number of grains per unit volume of the size class i withorientation

402 8 Computer Simulation of HTSC Microstructure and Toughening

A(orB);R and

A(B)

are the mean radius of grains in the whole system

and that with the orientation component A (or B), respectively:

R =

i=1

;

A(B)

i=1

A(B)

; (8.121)

= R

+ σ

;

A(B)



A(B)



, (8.122)

where σ and σ

A(B)

denote the standard deviations. The size class for a given

grain is found by the cell number, contained in this grain. The condition for

abnormal grain growth in the grain size class i with the orientation A (or B)

in the space (R, t), taking into account (8.117), is found as [245]

1/R

A(B)

∗

− 1/R

A(B)

/2 , (8.123)

where I

=6f

/(πr) is the value of the grain-growth stagnation, f

and r are

the volume fraction and mean radius of the secondary phase particles. It is

assumed that the stagnation parameter is independent of the grain orientation

and is calculated as described above. This parameter, as well as the critical

radii of the components A and B, governs the abnormal grain growth. This

circumstance enables us to deﬁne the HTSC ceramic properties and their

dependencies on the secondary phase characteristics.

The size parameters, which are necessary for calculations, are found in

the simulation of the primary re-crystallization. The orientations A and B are

distributed between grains, using the Monte-Carlo procedure, and they do not

change during growth. Moreover, it is assumed that mass transfer between

the grains of diﬀerent orientations is absent. As an example, we consider the

case of the next diﬀusion parameters for the orientation classes [2]: M

=2M

. This suﬃciently arbitrary selection is explained by

the absence of reliable test data for the Bi-2223 ceramic. The mass transport

between grains is simulated in accordance with the grain growth mechanism

at the non-singular surfaces [1034].

The computational algorithm for abnormal grain growth consists of the

following steps:

(1) The distribution of the orientations H (where H = A or B) between the

grains that are formed after primary re-crystallization.

(2) The deﬁnition of all neighbors for every grain of both orientation classes.

(3) The determination of adjacent grain couple in each orientation class

)with max

1≤i

≤N

1/R

− 1/R

(4) The growth of the larger grains from the (i

)attheexpenseofsmaller

ones.

(5) The checking of the conditions:

1/R

A(B)

∗

− 1/R

A(B)

≤ I

/2, where

=1,...,N

8.6 Toughening of Bi-2223 Bulk, Fabricated by Hot-Pressing Method 403

(6) End of the grain growth in the corresponding component H, if the condi-

tions (5) have been satisﬁed; else a change of the corresponding parameters

in (8.118)–(8.122) and fulﬁllment of the steps: (2)–(6) again.

The simulation of intergranular cracking due to cooling is carried out

as before, using (8.4) and (8.5) and the procedure described in detail in

Sect. 8.1.2.

8.6.2 Bi-2223 Toughening by Silver Dispersion

As has been noted above, an addition of Ag ductile phase dispersion to the

Bi-2223 ceramic causes a considerable increasing in the fracture resistance

of the superconductor compared to that of untoughened matrix. It is known

that the main mechanism responsible for enhanced toughness of brittle com-

posites with ductile particles appears to be the crack bridging by the ductile

phase. Here, we limit ourselves to the most important case for HTSC, when

an increasing of the ceramic toughness is independent of the particle size and

ductile strength. This corresponds to the state, when the ductile ﬂow has

occurred in a considerable zone near the crack tip. Then, the toughness in-

creasing due to the ductile particles (stationary crack case) can be estimated

as [988]



1 − ν

√



10(1 − ν

(7 − 5ν

)(1 − f

)



1/2

, (8.124)

where K

and K

are the fracture toughness with and without toughening,

respectively; f

is the ductile particulate concentration, deﬁned by the fraction

of this phase, intercepting the macrocrack path; ν

is eﬀective Poisson’s ratio,

deﬁned by the relative concentration of the Bi-2223 and Ag phases, and also

by the intergranular microcracks, formed during the composite processing.

Under conditions of the modiﬁed cubic model, we obtain [428]:

=(1− f

2/3

)ν

+ f

2/3

[ν

1/3

+ ν

(1 − f

1/3

)/E

]

1/3

+(1− f

1/3

)/E

]

, (8.125)

where the indexes m and c correspond to the metal inclusions and the ceramic

matrix. For the cracked matrix with a microcrack density, β

, Poisson’s ratio,

, and Young’s modulus, E

, are expressed as [892]

1+[(16/45)(1 − ν

)/(2 − ν

)]β

1+[(16/45)(1 − ν

)(10 − 3ν

)/(2 − ν

)]β

; (8.126)

=1/



16(1 − ν

)(10 − 3ν

)

45(2 − ν

)



, (8.127)

where ν

and E

are the intrinsic elastic modules.

Since the metallic inclusions have a greater thermal expansion than the

ceramic matrix [564], the residual tension (σ

) occurs in the metal, but the ce-

ramic is compressed. This internal stress state aﬀects the toughening, because

the compressive stresses in matrix must be exceeded within the bridging zone

404 8 Computer Simulation of HTSC Microstructure and Toughening

before beginning of crack opening. The additive increment of the toughness

is estimated as [988]

ΔG

≈ αf

∗

, (8.128)

where α(∼ 0.25) is a factor that depends on the precise nature of the func-

tion σ = σ(u); u

∗

is the total crack opening when the ductile material fails

(Fig. 8.35a). For cylindrical metal particles in a non-hardening material, the

axial residual stress, σ

, can be obtained as [444, 988]

ΔαΔT

∗

3(1 − 2ν

)+2(1+ν

)(E

)

, (8.129)

where Δα is the thermal expansion factor diﬀerence of the phases; ΔT

∗

is the

cooling thermal range, in which the rapid creep provides relaxation.

= σ

(a)

(b)

Fig. 8.36. (a) Scheme of crack (1) bridging by intercepted ductile silver particles (4);

the process (2) and stretch (3) zones of plastically distorted particles are shown (h

and L are the corresponding zone sizes; u

∗

is the residual crack opening at link failure

and σ

is the yield strength) [988]; (b) a model fragment of Bi-2223/Ag composite

with the Bi-2223 grains (5) and cooling microcracks (6); macrocrack is denoted by

gray line

8.6 Toughening of Bi-2223 Bulk, Fabricated by Hot-Pressing Method 405

Table 8.9. Numerical results [577]

D/δ β

/b f

2.40 0.15 1.51 0.12 1.96

2.84 0.22 1.62 0.10 1.92

It has been suggested in computer simulations that the silver inclusions

are localized at the triple junctions, where there are usually microdefect sites,

healed by the Ag. The necessary parameters for Ag particles are given else-

where [845]. The optimum Ag volume concentration in the Bi-2223 bulk is

assumed to be f

=0.2 [564]. Finally, we modeled the intergranular macro-

crack path (see Fig. 8.36b), using Viterbi’s algorithm for graphs [796, 823],

taking into account the grain structure and processing microcracks.

Statistically reliable results during computer simulations are obtained

again by application of the stereological method [145]. In order to deﬁne more

accurate estimations of the eﬀects of dispersed Ag particles on the strength

properties, we assumed that other toughening mechanisms, considered above,

are absent. We obtain numerical results for values of I

=2.0and1.2(ﬁrst

and second line in Table 8.9, respectively), where D

is the grain size before

the grain growth. In the macrocrack simulation which propagates along the

intergranular boundaries of the Bi-2223 matrix, the value of f

is found, tak-

ing into account the macrocrack length, the number of triple junctions (or Ag

particles) in the crack path and the relationship between the defect size (2a)

and critical boundary size (l

), namely: a =0.1l

,whichisthesameasthat

for a ceramic with TEA [260]. As it follows from (8.128), the value of f

is pro-

portional to the toughness diﬀerence, ΔG

. At the same time, a decreasing of

the parameter I

leads to increasing of the matrix grain size and correspond-

ing enhancement of the microcracking density (β

). Moreover, the number of

triple points also decreases with the increasing of the relative macrocrack size

/b,wherel

is the macrocrack size, and b is the specimen width due to the

longer path, required around the larger grains. The latter causes a decreasing

of f

and corresponding decreasing of ΔG

. Finally, the smaller values of β

increase the elastic modules and together with the increased concentration of

lead to increasing of K

at decreasing of the grain size.

Mechanical Destructions of HTSC Josephson

Junctions and Composites

As it has been shown in Chap.1, Josephson eﬀects are connected with a

behavior of weak links of superconductors. According to the classiﬁcation

of high-temperature superconducting Josephson junctions (HTSC JJs), pre-

sented in Sect. 1.7, special interest from view of strength and fracture tough-

ness is excited by the junctions with intrinsic barriers or interfaces, formed

by the intergranular boundaries with diﬀerent crystallographic orientations,

and also HTSC JJs with extrinsic interfaces in the fabrication of which, the

artiﬁcial normal metallic or insulating barriers are used. The strength prob-

lems of the JJs, having the extrinsic interfaces (see Fig. 9.1), cause their small

eﬀective superconducting area as compared with the geometrical square and

can lead to the large parameter spreads. The microstructure destruction can

be found by some causes, namely by the deformation (lattice) mismatches and

thermal expansion anisotropy [17, 554], by exceeding the critical ﬁlm thick-

ness [314, 929], by the misorientation eﬀects [314], by the rough or damaged

interfaces [929], etc.

The use of buﬀer layers (e.g., CeO

, MgO, YSZ, ZrO

, SrTiO

[981]) has

enabled the increase of superconducting and transport properties of HTSC

composite structures due to diminution of TEA and lattice mismatches be-

tween HTSC ﬁlm and substrate and also owing to decrease of a chemical

reactivity of the substrate. Nevertheless, the problems of critical mechanical

behavior for these laminated structures under conditions of existence of resid-

ual stresses and external loads remained in the center of attention of HTSC

JJ researchers and engineers.

This chapter presents a set of models for estimation of strength properties

for HTSC composites of S-I-S and S-N-S (where S is the superconductor, I is

the isolator, N is the normal metal) types, based on the consideration of inter-

faces, taking into account TEA, geometrical and material parameters, external

loads and residual stresses. Moreover, features of the mechanical damage of

HTSC composites and proper fracture resistance mechanisms are considered

[802, 804, 807].

408 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

Fig. 9.1. Cross-section of HTSC JJ, consisting of nine layers, on NdGaO

substrate:

1 – buﬀer layer (30 nm), 2 – YBCO base layer (150 nm), 3 – transitional supercon-

ducting layer (150 nm), 4 – SrTiO

epitaxial dielectric (150 nm), 5 – YBCO top

layer (150–200 nm), 6 – non-epitaxial silicon nitride dielectric (250 nm), 7 – silver

contact layer (600 nm), 8 – molybdenum resistor (90 nm) and 9 – silver wiring layer

(600 nm) [751]

9.1 Interface Fr acture

The interface roughness in HTSC bimaterial and a crack growth near and at

the interface introduce inevitably a mixed loading mode. In this case, there

are some morphological features of fracture [263, 485, 979], shown in Fig. 9.2,

namely (i) an interface fracture; (ii) a crack growth into more brittle compo-

nent; (iii) an alternative fracture along interface or between the interface and

adjacent material; and (iv) a crack deﬂection from one interface to an other.

The experiments on various materials have shown that the crack path is found

by both the ratio of interface fracture energy to fracture energy of more brit-

tle component (Γ

/Γ

) and the phase angle of loading, Ψ =arctg(K

where K

and K

is the SIF of I and II mode, respectively. On the other hand,

this angle can be coupled with the ratio of displacements – the shear to the

opening (i.e., to the ratio of ν/u) due to the insertion of Dunders parameters

(α and β) as [236]

Ψ =arctg(ν/u)−∈

ln r − arctg(2 ∈

) , (9.1)

where

∈

2π



1 − β

1+β



; (9.2)

α =

(1 − ν

) − μ

(1 − ν

)

(1 − ν

)+μ

(1 − ν

)

; β =

(1 − 2ν

) − μ

(1 − 2ν

)

2[μ

(1 − ν

)+μ

(1 − ν

)]

; (9.3)

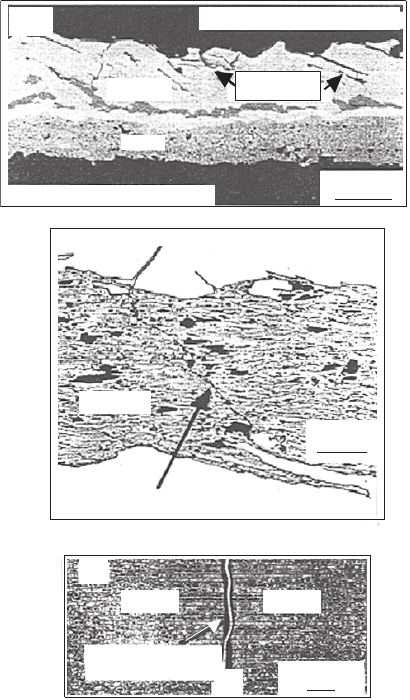
9.1 Interface Fracture 409

Alumina

YSZ

YBCO

Cracks

30 μm

Silver

Crack

BSCCO

10 μm

460 μm

Interface Crack

(a)

(b)

(c)

Fig. 9.2. Characteristic morphology of possible fractures at and near interfaces

into HTSC composite structures: (a) interface fracture and an alternative fracture

between the interface and adjacent material (SEM cross-sectional micrograph of

YBCO thick ﬁlm, processed on YSZ barrier layer on alumina [979]), (b)crackgrowth

into more brittle component (Back-scattered electron image of transversal cross-

section of BSCCO/Ag tape [485]) and (c)crackinAl

bonded with Au, showing

a crack alternating between interfaces [263]

and ν

(k =1, 2) are the shear modulus and Poisson’s ratio, respec-

tively, for k-component and r is the distance measured from the crack tip at

the interface. The parameter of α together with the dependence of Γ

/Γ

Ψ enables to separate the areas of the interface crack and the brittle substrate

fracture in the case of an initial crack at the interface. Then, the fracture

410 9 Mechanical Destructions of HTSC Josephson Junctions and Composites

behavior and the interface fracture energy are very sensible to a sign of the

phase angle at the great diﬀerence of the fracture energies for both components

(Γ

>> Γ

). In the case of the positive value of Ψ, there are both regimes,

namely the interface cracking and a crack deﬂection into more brittle com-

ponent, depending on the parameter α. The second case (when Ψ<0) is

more interesting. Therein, the greater value (i.e., Γ

) is compared with the

interface fracture energy Γ

. As the condition Γ

>> Γ

prohibits crack propa-

gation away from the interface, then there are two cases. For the low material

strength, a plastic bluntness of the crack at the interface occurs and the failure

features are caused by the toughening mechanisms, including an initiation of

voids at the interface.

In the contrary case, the stress state of the interface

crack interacts with microcracks and structural defects which as rule exist

in the brittle material and provoke a growth of microcracks in the direction

to the interface. This causes a saw-tooth fracture, with chips of the brittle

material attached to the interface (see Fig. 9.3).

Further more, because the complete smoothness of the interfaces is impos-

sible (e.g., see Fig. 9.4a), an estimation of the JJs fracture resistance depending

on the interface roughness is the actual problem. The crack surfaces, grow-

ing along the interface, contact each other either at the roughness or at the

facets. In this case, it is possible to obtain diﬀerent values of the interface frac-

ture resistance, which grow with the phase angle of loading, Ψ. These eﬀects

have been observed and estimated for diﬀerent brittle materials [266, 482]. In

particular, a comparative analysis of microstructure properties and fracture

parameters, caused by the mixed loading mode, has been fulﬁlled for the ﬁne-

grain (PbTiO

) and coarse-grain (BaTiO

) ferroelectric ceramics [816]. The

decrease of the strain energy release rate (or crack shielding) ΔG = G − G

(where G and G

are the values of the strain energy release rate connected

with applied load and at the crack tip, respectively) can be estimated using

two models: (i) the contact zone of the crack surfaces taken into account, but

without account of Coulomb’s friction [266], and (ii) the inclination angle of

the faceted interface, δ, is taken into account [482]. We have for the ﬁrst model

(see Fig 9.4b) [266]:

ΔG/G =[1− λ

−2

(α)]tg

Ψ/(1 + tg

Ψ) , (9.4)

where α =(L/l

)/ ln[1/ sin(πD

/2l

)]. The values of the function, λ(α),

for various values of α have been tabulated in [101]. The length of the con-

tact zone, L, is found by L =(π/32)[EH/(1 − ν

]

.Herel

is the

spacing between the facet centers, D

is the facet length and H is the

height of the interface step. The numerical approximation is obtained, tak-

ing into account the typical geometry of undulating interfaces, assuming that

At the same time, note that those intergranular voids formed, for example, by

thermo-mechanical treatment during a multi-stage processing of monocore Bi-

2223 tapes, may become the main cause of critical current diminution in the case

of prolonged ﬁnal annealing [801]

9.1 Interface Fracture 411

Interface

Cracks

−

1.4

−

1.2

0.8

−

0.6

−

0.4

−

0.2

−

−π/8

π/8 π/4 3π/2 π/2

Interface

Cracking of

Substrate

Fracture of

Interface

Phase Angle of Loading, Ψ

Relative Toughness, Γ

/ Γ

Fig. 9.3. Fracture at interface into bimaterial for Γ

>> Γ

(result in the case

of α = β = 0). When phase angle, Ψ<0, the interface fracture demonstrates

near-boundary segments of material free from cracks [263]

∼ 1/2; H/l

∼ 1/2; equating K

to the fracture toughness, K

(which

is approximately equal to 1 MPa ·m

1/2

for a broad set of ceramics), and intro-

ducing a material parameter, χ = E

H/(1 −ν

, which deﬁnes the length

of the contact zone, L. Note that the parameter χ in total causes a fracture

behavior in this microstructure consideration. Therefore, one should be mea-

sured with a high accuracy in order to obtain acceptable results for the HTSC

JJs. For example, the value of χ ≈ 100 has been found for the glass–polymer

interface [266].

We obtain for the second model (Fig. 9.4c) [482]:

ΔG/G =(cosδ sin Ψ − sin δ cos Ψ)

,Ψ>δ; H>>a, (9.5)