Островський А.Л., Мороз О.І., Тарнавський В.Л. Геодезія, частина II
Подождите немного. Документ загружается.


Знайдемо середнє вагове значення висоти точки
Е:
Далі, знаючи зрівноважену висоту вузлової точки Н
Е
, знайдемо
нев'язки кожного з ходів: Д, Д, Д за формулами:
Д=я,-я
£
,д
=
я
2
-я
е
,д=я
3
-я
£
.
Подальше зрівноваження кожного із цих ходів можна виконати
описаним вище методом. Залишається оцінити точність нівелювання за
результатами зрівноваження. Знайдемо середню квадратичну похибку
одиниці ваги - /і для випадку, коли у одну вузлову точку сходяться и -
ходів. Тоді, як відомо,
РУУ•
її!
(1.4.10)
и-1
де (п -1) - кількість надлишкових ходів;
Р
(
- ваги ходів;
V, - поправки ходу, отримані зі зрівноваження.
Щоб знайти висоту точки Е, достатньо прокласти один хід.
Якщо
Р
{
;
= —, то ц - похибка ходу, довжиною в 1 км; якщо ж
р. = —, де С - довжина деякого ходу в км, то = ; у цих двох
випадках похибка нівелювання на одній станції и = ; якщо ж ^ = —,
VI о и і
то /л - похибка нівелювання на одній станції. Тоді, = /і
сл1
>/Ї0 . Нарешті,
С Ц
якщо % = —, то ц - похибка ходу, що має С станцій; м
С
т~~г- °
и,. VС
останньому випадку похибка ходу, довжиною в
1
км буде:
Похибку визначення висоти вузлової точки Е знаходять за формулою:
1.4.3. Зрівноваження перевищень нівелірних мереж методом
еквівалентної замш
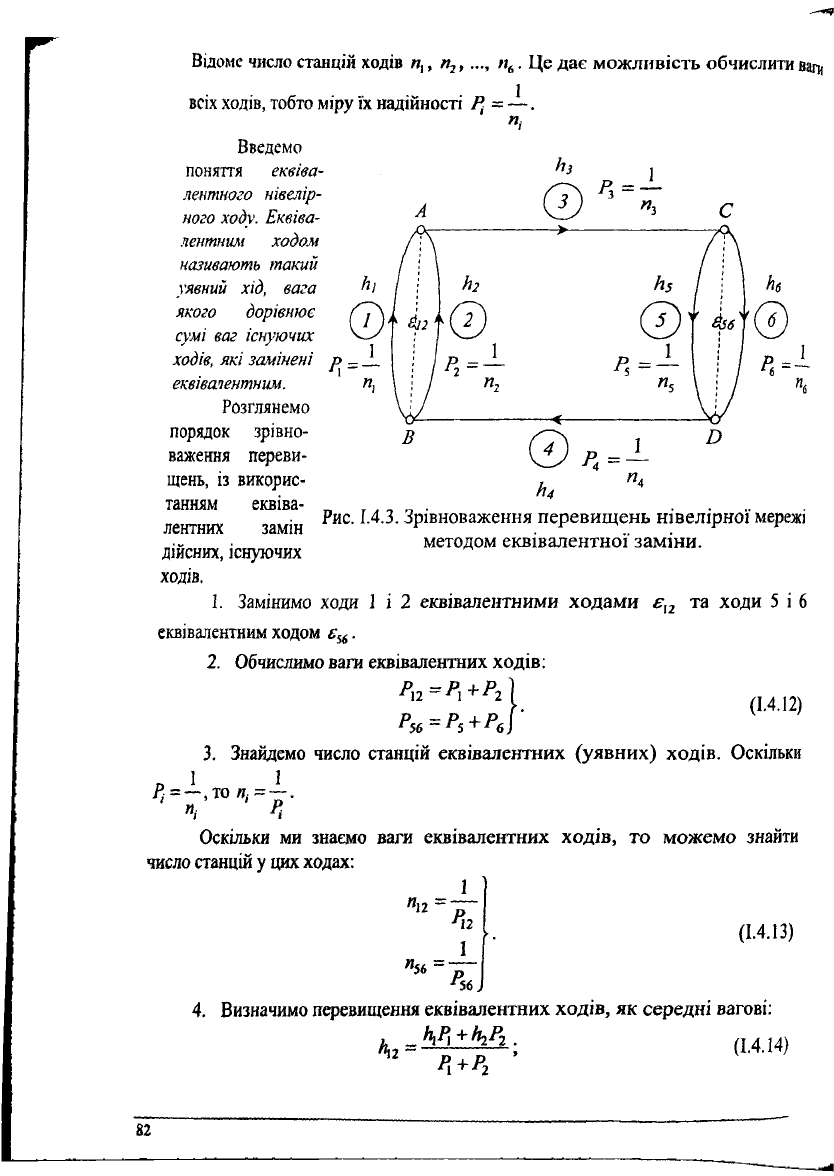
Візьмемо нівелірну мережу, показану на рис. 1.4.3. Мережа має 4
вузлові точки А, В, С, й. Висоти цих точок невідомі. Між вузловими
точками прокладено 6 ходів. В ходах виміряні перевищення й,, ^, Н
ь
.
81
Відоме число станцій ходів и,, п
г
,..., п
6
. Це дає можливість обчислити
і
всіх ходів, тобто міру їх надійності Р
і
—
1
пі
Введемо
поняття еквіва-
лентного
нівелір-
ного ходу. Еквіва-
лентним ходом
називають такий
уявний хід, вага
якого дорівнює
сумі ваг
існуючих
ходів,
які
замінені
р _
еквіваїентним.
Розглянемо
порядок зрівно-
важення переви-
щень, із викорис-
танням еквіва-
лентних замін
дійсних, існуючих
ходів.
1. Замінимо ходи 1 і 2 еквівалентними ходами є
хг
та ходи 5 і 6
еквівалентним ходом є
56
.
2. Обчислимо ваги еквівалентних ходів:
и.
Рис. 1.4.3. Зрівноваження перевищень нівелірної мережі
методом еквівалентної заміни.
Р
п
=Р
х
+Р
г
(1.4.12)
3. Знайдемо число станцій еквівалентних (уявних) ходів. Оскільки
р
1 1
И,
л
Оскільки ми знаємо ваги еквівалентних ходів, то можемо знайти
число станцій у цих ходах:
1
"12=-
Пг
1
"56=-
Г
56)
(1.4.13)
4. Визначимо перевищення еквівалентних ходів, як середні вагові:
= М±М_
;
(1.4.14)
/?+/»
2
82

и
56
-
(1.4.15)
Після заміни ходів 1,2- еквівалентними ходами є
и
, та ходів 5, 6 -
еквівалентним ходом є
}6
, мережа перетворилася у зімкнений хід - полігон.
5. Знайдемо нев'язку полігону /
н
та число станцій полігону -
п:
Л=А» +
'Ь
+ ''
5
. +
'>4.
0.4.16)
п = п
и
+ п
і
+ п
і6
+ п
л
. (1.4.17)
6. Визначимо нев'язки чотирьох ходів, що залишилися після заміни:
еквівалентних є
п
, е
56
та існуючих - 3,4:
А„ -~
п
и'' Д, -~'"5б
11
и
41
и
Л,=—и
3
; Л=-«4
' и ' п
(1.4.18)
7. Знаючи нев'язки ходів 3 і 4, знайдемо їх зрівноважені переви-
щення як поодиноких ходів:
8. Аналогічно знайдемо зрівноважені перевищення еквівалентних
ходів:
^12 зв -Д
2
І
^56зв ~Д
6
]
9. Визначимо нев'язки ходів 1 і 2 та 5 і 6:
Д
|
Д
=Л
2-^2м| '
Д =
А
5-
А
56
И
]
Д =
А
6-
А
56З»|
10. На рисунку не показано, але в кожному із шести ходів є репери.
Тепер, коли дана мережа розділилась на шість незалежних ходів і відомі
нев'язки цих ходів, то в подальшому врівноважують перевищення між цими
реперами, пропорційно вагам частин ходів між суміжними реперами. Ці
ваги обернено пропорційні числу станцій у секціях. Зрівноваження завер-
шують оцінкою точності результатів. Похибка одиниці ваги знаходять за
формулою:
(1.4.19)
(1.4.20)
(1.4.21)
(1.4.22)
\п-к '
де п - число всіх ходів; к - число вузлових точок.
(1.4.23)
83
Різниця г = (п-к) дає число надлишкових ходів. У нашому випадку:
г =6-4 = 2. Мережа мас два надлишкових ходи.
1.4.4. Зрівноваження висот нівелірних мереж методом еквівалентної
заміни
Методом еквівалентної заміни можна зрівноважувати не тільки
перевищення, але й висоти точок, числові величини яких називають відміт-
ками.
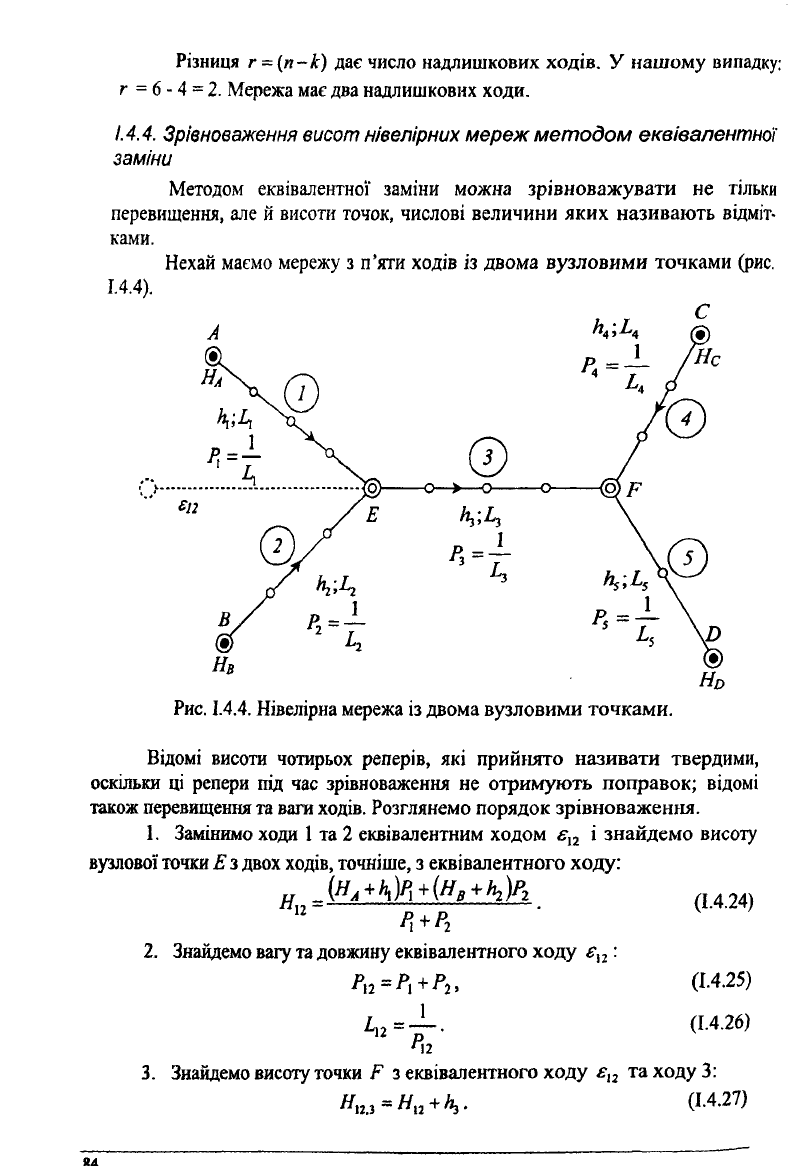
Нехай маємо мережу з п'яти ходів із двома вузловими точками (рис.
1.4.4).
Рис. 1.4.4. Нівелірна мережа із двома вузловими точками.
Відомі висоти чотирьох реперів, які прийнято називати твердими,
оскільки ці репери під час зрівноваження не отримують поправок; відомі
також перевищення та ваги ходів. Розглянемо порядок зрівноваження.
1. Замінимо ходи 1 та 2 еквівалентним ходом є
п
і знайдемо висоту
вузлової точки Е з двох ходів, точніше, з еквівалентного ходу:
(Н
А
+Н
І
)Р
1
+ (Нд
я,, = .
Р
1+
Р
г
2. Знайдемо вагу та довжину еквівалентного ходу є
п
:
Р
п
= Р
1
+
Р
2
,
1
(1.4.24)
Ь
п
(1.4.25)
(1.4.26)
42
3. Знайдемо висоту точки Р з еквівалентного ходу є
12
та ходу 3:
Я„
3
=Я
и +
Аз. (1.4.27)
ЯЛ

ж
Тепер, по-суті, ми маємо мережу з однією вузловою точкою - Р.
Знайдемо найімовірніше значення висоти цієї точки:
Н
р
=
+ + +
+
> (1428)
де І
123
=£
12
+£
3
, а
Пг.з +
^ + Р,
Л2,з=~- (1.4.29)
^12,3
4. Знаючи зрівноважене значення висоти точки Р, знайдемо нев'язки
ходів, що сходяться у цій точці:
(1.4.30)
Л,=(Яс + А
4
)-^. ("-ЗІ)
(1.4.32)
5. Розділимо нев'язку Д на нев'язки еквівалентного ходу є
п
та
ходу 3, враховуючи довжини цих ходів:
Аг ~ , ^т
і,
2
+^3
(1.4.33)
6. Тепер є можливість вирахувати зрівноважену висоту точки £ -
Я
£
з контролем:
Н
Е
=Н
Х1
-Д
2
, (1.4.34)
Н
Е
=Н
Р
-Нз-Д. (1.4.35)
7. Залишається знайти нев'язку початкових ходів
1
та 2:
А
=(Н
А
+Н,)-Н
В
]
* , ' . (1.4.36)
Оцінку точності виконують, як звичайно.
1.4.5. Зрівноваження нівелірних мереж способом послідовних
наближень (спосіб вузлів)
Розглянемо застосування цього способу для мережі, що складається із
шести ходів, які створюють три вузлових точки (рис. 1.4.5). Відомі переви-
щення та довжини ходів, висоти трьох реперів, обчислені ваги ходів.
Припустимо, що якимось чином знайдені висоти вузлових точок X, У,
2. Але, якщо знайдені висоти цих точок, то для кожного ходу можна скласти
рівняння похибок.
85
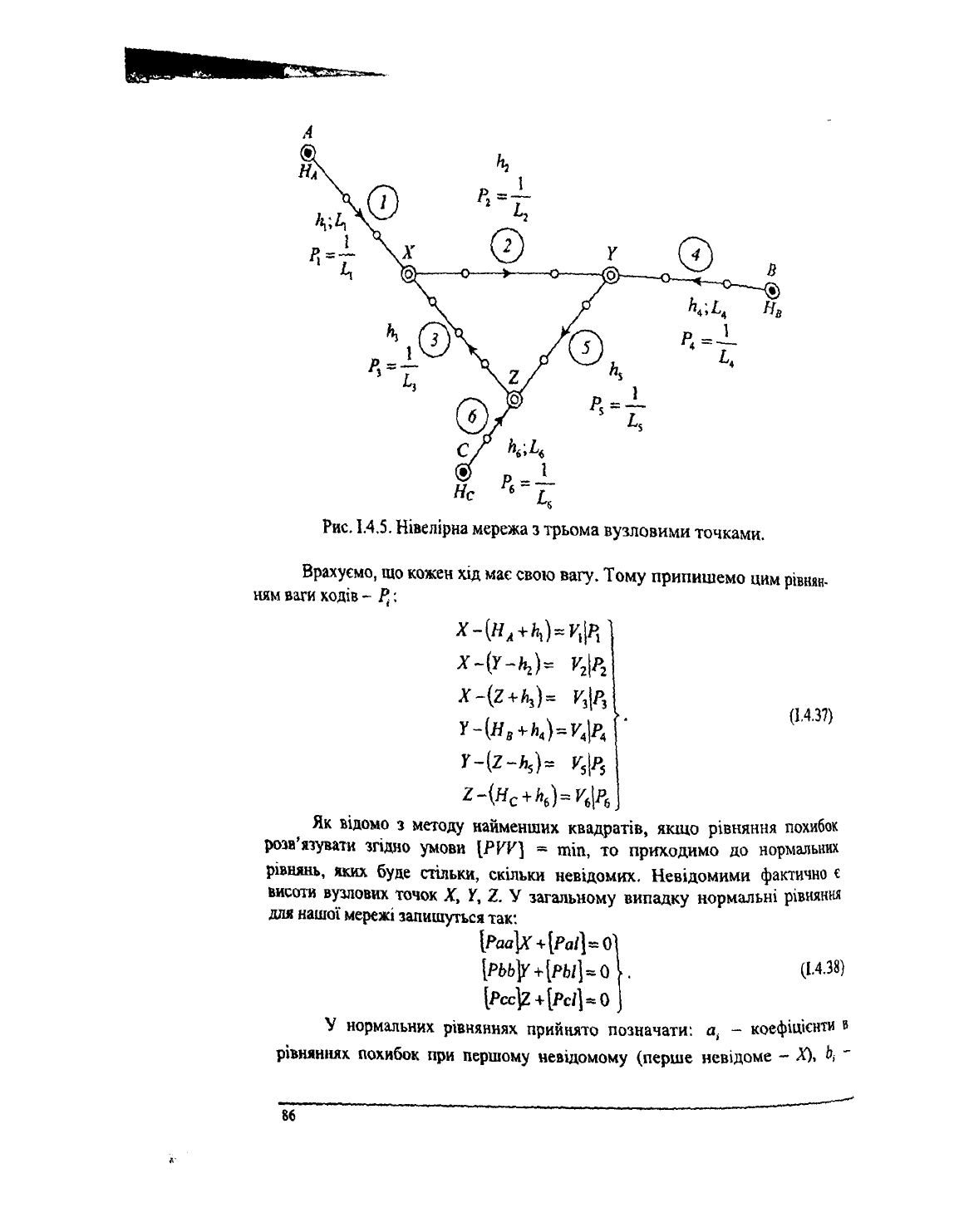
Рис. 1.4,5. Нівелірна мережа з трьома вузловими точками.
Врахуємо, що кожен хід має свою вагу. Тому припишемо цим рівнян-
ням ваги ходів - Р
(
:
Як відомо з методу найменших квадратів, якщо рівняння похибок
розв'язувати згідно умови [РУУ] - тіп, то приходимо до нормальних
рівнянь, яких буде стільки, скільки невідомих. Невідомими фактично €
висоти вузлових точок X, У, 2. У загальному випадку нормальні рівняння
дня нашої мережі запишуться так:
У нормальних рівняннях прийнято позначати: а
і
- коефіцієнти в
рівняннях похибок при першому невідомому (перше невідоме - X), Ь,'
(14.37)
(1.4.38)

відповідні коефіцієнти при другому невідомому
—
У; с,
—
при третьому
невідомому - 2. Як видно з (1.4.37), коефіцієнти при Х,У,2- одиниці, тобто:
а,
3
ь
>
=
с
, =
1
;
- вільні члени, відомі частини рівнянь;
і, = ~{н
А
+л,); =
-(у-М
;
- '«- +Ьв).
Перше нормальне рівняння системи (1.4.38) у розгорнутому вигляді
запишеться так:
Р,Х + Р
2
Х
+
Р
г
Х - (н
л
+ Н
[
)Р
1
-{У-Н
2
)Р
2
-(г
+
Н
і
)Р
і
= 0. (І.4.39)
Розв'яжемо це рівняння відносно невідомого X:
+
(
і440)
Р
х
+Р
г
+ Р
г
Аналізуючи (1.4.40), зауважимо, що невідоме X визначається як
середнє вагове з трьох ходів, що сходяться у вузлову точку. Тепер, не
записуючи інші два нормальні рівняння в розгорнутому вигляді, можемо, за
аналогією з (1.4.40), записати формули для знаходження невідомих У та 2:
у=
{Х
+
к
1
)Р^{Н
в+
Н,)Р,
+
(2-Ь
і
)Р
іі
г =
{Х-Ь
г
)Р
г
+(У
+
Ь
і
)Р
і
+ (Н
с
+ к
6
)Р
6
Оскільки в рівняннях (1.4.40), (1.4.41), (1.4.42) є невідомі, як у лівій,
так і в правій частині, то безпосереднє розв'язання цих рівнянь неможливе.
Дійсно, наприклад, у (1.4.40), в лівій частині невідоме - X, а в правій -
невідомі У та 2. Те саме у двох інших рівняннях. Але ці рівняння можна
розв'язувати способом послідовних наближень, тобто способом ітерацій.
Для цього спочатку знайдемо наближені значення невідомих висот вузлових
точок, використовуючи відомі репери, що розташовані найближче до
шуканих:
^ = Нл + \; К
Р
= Я
в
+
А
4
;
2
лр
=Н
С +
И
6
.
У рівняння (1.4.40) підставимо наближені значення У^ та 2
Щ
.
Знайдемо Х
х
із першого наближення. Далі, під час розв'язування рівняння
(1.4.41), підставляємо не Х„
р
, а значення Х
{
- із першого наближення.
Знайдемо . Визначаючи 2 з рівняння (1.4.42), будемо підставляти не Х^,
У„
р
, а Х
1
та У,. Тоді знайдемо з першого наближення 2,.
Переходимо до другого наближення: визнаючи X, підставляємо в
(1.4.40) значення У,, 2, і так далі.
Зазвичай, достатньо зробити 3-4 наближення. Процес ітерації закін-
чують, якщо в останньому й передостанньому наближенні значення неві-
домих однакові. Зрозуміло, що такий метод придатний для мережі зі
87
значною кількістю ходів та вузлових точок. Рівняння для визначення
невідомих висот реперів складають безпосередньо зі схеми нівелірної
мережі. Тому, цей спосіб знайшов широке застосування у виробництві.
Обчислення проводять на персональних комп'ютерах.
1.4.6. Зрівноваження нівелірної мережі порівнянням нев'язок суміжних
ходів
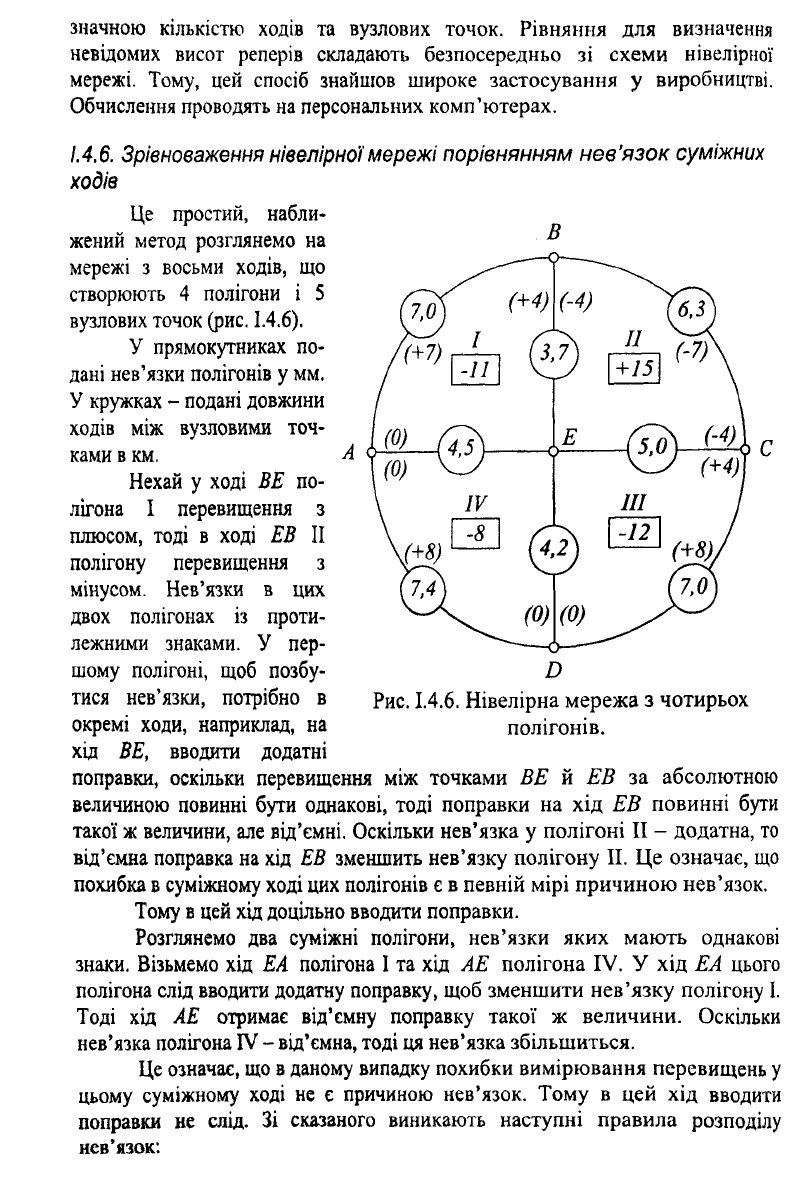
Це простий, набли-
жений метод розглянемо на
мережі з восьми ходів, що
створюють 4 полігони і 5
вузлових точок (рис. 1.4.6).
У прямокутниках по-
дані нев'язки полігонів у мм.
У кружках - подані довжини
ходів між вузловими точ-
ками в км.
Нехай у ході ВЕ по-
лігона 1 перевищення з
плюсом, тоді в ході ЕВ II
полігону перевищення з
мінусом. Нев'язки в цих
двох полігонах із проти-
лежними знаками. У пер-
шому полігоні, щоб позбу-
тися нев'язки, потрібно в
окремі ходи, наприклад, на
хід ВЕ, вводити додатні
поправки, оскільки перевищення між точками ВЕ й ЕВ за абсолютною
величиною повинні бути однакові, тоді поправки на хід ЕВ повинні бути
такої ж величини, але від'ємні. Оскільки нев'язка у полігоні II - додатна, то
від'ємна поправка на хід ЕВ зменшить нев'язку полігону II. Це означає, що
похибка в суміжному ході цих полігонів є в певній мірі причиною нев'язок.
Тому в цей хід доцільно вводити поправки.
Розглянемо два суміжні полігони, нев'язки яких мають однакові
знаки. Візьмемо хід ЕА полігона І та хід АЕ полігона IV. У хід ЕА цього
полігона слід вводити додатну поправку, щоб зменшити нев'язку полігону І.
Тоді хід АЕ отримає від'ємну поправку такої ж величини. Оскільки
нев'язка полігона IV - від'ємна, тоді ця нев'язка збільшиться.
Це означає, що в даному випадку похибки вимірювання перевищень у
цьому суміжному ході не є причиною нев'язок. Тому в цей хід вводити
поправки не слід. Зі сказаного виникають наступні правила розподілу
нев'язок:
В
Рис. 1.4.6. Нівелірна мережа з чотирьох
полігонів.

1. Якщо у двох суміжних полігонах нев'язки з протилежними
знаками, то в суміжний хід слід вводити однакові поправки з
протилежними знаками і зменшити нев'язки цих полігонів;
2. Якщо у двох суміжних полігонах нев'язки з однаковими знаками,
то в суміжні ходи не можна вводити поправки;
3. Абсолютні значення поправок повинні бути прямо пропорційні
довжині ходів, що створюють полігон.
Користуючись цими правилами, зрівноважимо мережу, подану на
рис. 1.4.6. Почнемо з полігона І, У хід ЕА вводити поправку не слід. Тому
поправки в цей суміжний хід дорівнюють нулеві. Нев'язка -11 мм припадає
на два ходи. Хід АВ - довший порівняно з ходом ВЕ. Тому розподілимо
нев'язку так: на хід ВЕ - +4 мм; на хід АВ - +7 мм. Поправки на рисунку
взяті у круглі дужки. Перший полігон ув'язано.
Перейдемо до полігону II. Полігон отримав поправку -4 мм.
Залишилась нев'язка +11 мм. Поправки на два інші ходи цього полігона
будуть -4 мм та -7 мм.
Перейдемо до полігону III. Тут залишилась нев'язка -8 мм. У хід ОЕ
вводити поправки не можна, залишок нев'язки слід ввести в зовнішній хід
С£> - +8 мм.
Нарешті, розглядаємо полігон IV. Два ходи цього полігона отримали
нульові поправки. Це означає, що всю нев'язку слід ввести в зовнішній хід
ЬА - +8 мм. Мережа ув'язана.
Спосіб простий, оскільки зрівноваження виконують безпосередньо на
схемі мережі, практично без обчислень і, за певного досвіду, спосіб дає
результати, що часто задовольняють інженерну практику.
1.4.7. Зрівноваження нівелірної мережі методом В.В.Попова
Професор В.В.Попов вдосконалив розглянутий нами спосіб порів-
няння нев'язок так вдало, що він став точним. Розглянемо суть цього спо-
собу на тій самій мережі, що подано на рис. 1.4.6. Мережа зображена у
збільшеному вигляді на рис. 1.4.7. Спосіб, названий автором способом
полігонів, зводиться до послідовного розподілення нев'язок у кожному
полігоні пропорційно вагам окремих ходів, приведених до одиниці. Ці ваги
називаються червоними числами, оскільки на схемах мереж вони випи-
суються червоним кольором.
Розглянемо, як обчислюють червоні числа (приведені ваги) на прик-
ладі полігону І. Периметр полігона 1-15,2 км, а хід АВ має довжину 7,0 км.
15,2 7
Складемо пропорцію: , Х
ЛВ
= 0,46; 0,46 і є приведена
вага ходу АВ.
15 2 3 7
Для ходу ВЕ відповідно знайдемо: —— = —і—, Х
ВЕ
=0,24.
1 Хве
Аналогічно знайдемо вагу ходу ЕА. Вона становить Х^ - 0.30.
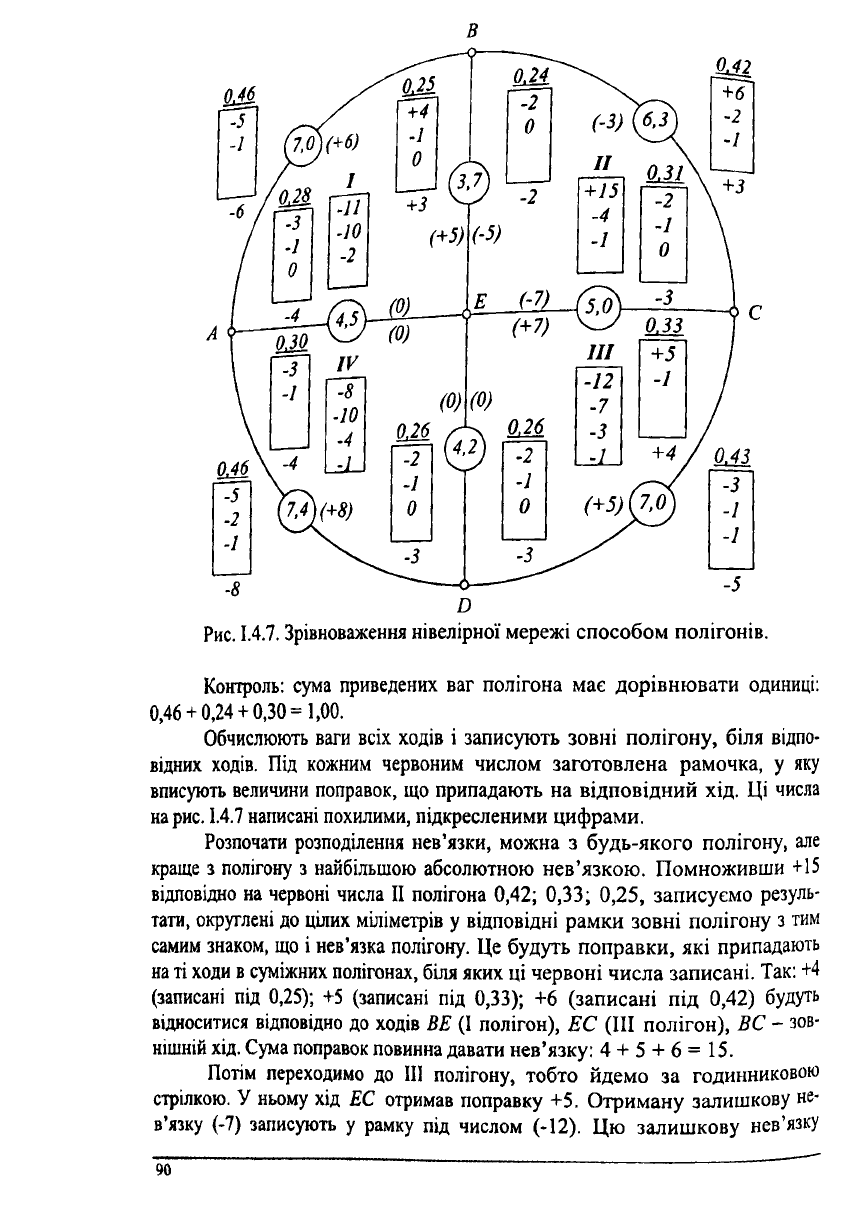
в
Контроль: сума приведених ваг полігона має дорівнювати одиниці:
0,46 + 0,24 + 0,30=1,00.
Обчислюють ваги всіх ходів і записують зовні полігону, біля відпо-
відних ходів. Під кожним червоним числом заготовлена рамочка, у яку
вписують величини поправок, що припадають на відповідний хід. Ці числа
на рис. 1.4.7 написані похилими, підкресленими цифрами.
Розпочати розподілення нев'язки, можна з будь-якого полігону, але
краще з полігону з найбільшою абсолютною нев'язкою. Помноживши +15
відповідно на червоні числа II полігона 0,42; 0,33; 0,25, записуємо резуль-
тати, округлені до цілих міліметрів у відповідні рамки зовні полігону з тим
самим знаком, що і нев'язка полігону. Це будуть поправки, які припадають
на ті ходи в суміжних полігонах, біля яких ці червоні числа записані. Так: +4
(записані під 0,25); +5 (записані під 0,33); +6 (записані під 0,42) будуть
відноситися відповідно до ходів ВЕ (І полігон), ЕС (III полігон), ВС - зов-
нішній хід. Сума поправок повинна давати нев'язку: 4 + 5 + 6=15.
Потім переходимо до III полігону, тобто йдемо за годинниковою
стрілкою. У ньому хід ЕС отримав поправку +5. Отриману залишкову не-
в'язку (-7) записують у рамку під числом (-12). Цю залишкову нев'язку
90
