Островський А.Л., Мороз О.І., Тарнавський В.Л. Геодезія, частина II

Подождите немного. Документ загружается.

множимо на червоні числа полігона III і результати (-2), (-2), (-3) записуємо

у відповідні рамки полігона III, що розташовані зовні цього полігона. Далі

переходимо до четвертого полігона. У ньому була нев'язка (-8), але хід £0

отримав поправку (-2). Тому сумарну нев'язку (-10) записують під почат-

ковою нев'язкою (-8). Нев'язку (-10) множать на червоні числа полігону IV і

записують у рамки зовні цього полігона (-5), (-3), (-2).

Нарешті, переходимо до І полігону. У ньому поправки мають два

ходи: хід ВЕ (+4) та хід ЕА (-3). Тому нев'язку (-11) виправимо на суму цих

поправок. Отримаємо (-10), які записуємо під (-11). Нев'язку (-10) множимо

на червоні числа І полігона, записуючи відповідні поправки (-5), (-3), (-2) у

відповідні рамки. На цьому завершується перше коло розподілення нев'язок.

Переходимо до другого кола, все повторюючи в тому ж порядку і

починаючи з полігона II. У цьому полігоні нев'язку ми вже розподілили, але

потім ходи СЕ й ЕВ отримали нові поправки (-2) і (-2). Склавши їх, отри-

маємо нову нев'язку - (-4) цього полігона. Нову нев'язку розподіляємо так

само, як описано вище, вписуючи вторинні поправки ходів у відповідні

рамки. Аналогічно розподіляємо вторинні нев'язки в усіх полігонах і

переходимо до наступного кола. У нашому випадку необхідно було зробити

три кола. Тепер залишається в кожній рамці під червоними числами

обрахувати алгебраїчну суму поправок. Для периферійних ходів потрібно в

алгебраїчній сумі поміняти знаки на зворотні й отримані таким чином числа

записати в середині відповідного полігона біля відповідного ходу.

Наприклад, для ходу АВ маємо зовні -6, тоді ми повинні записати (+6). Для

розпізнавання поправок у ходи записуємо їх у круглі дужки.

Для внутрішніх ходів кожної пари суміжних полігонів є по дві рамки,

розміщені по різні сторони ходу. Так, для ходу СЕ рамка в середині II

полігона дає поправку (-3), а для ходу ЕС- рамка в середині полігона III, дає

поправку (+4), що під час переводу на хід СЕ дає (-4). Склавши (-3) і (-4), ми

знайдемо загальну поправку ходу СЕ, рівну (-7). Для ходу ЕС поправка

дорівнюватиме (+7). Ці дві величини ми і вписуємо біля даного ходу, кожну

в середині відповідного полігону. Контролем знайдених поправок є те, що їх

сума має давати початкову нев'язку з оберненим знаком.

Зазначимо, що якщо розподіл нев'язок виконувався б із заокруглен-

ням до десятих частин мм, то поправки деяких ходів змінились би тільки на

1 мм, однак, потрібно було б зробити шість кіл, що не виправдовує затрати

потрібного для цього майже вдвоє більшого часу.

Порівнюючи рис. 1.4.6 і рис. 1.4.7, бачимо, що

деяких ходах поправки,

отримані двома способами, відрізняються. Спосіб порівняння нев'язок, як уже

відзначалось, наближений і застосовували ми його спрощено, не дотри-

муючись точної пропорційності поправок і довжин ходів. Проте, на цьому

прикладі ми бачимо, що розподіл нев'язок наближеним способом виконується

приблизно так, як і строгим способом. Нульові поправки отримали ті самі

ходи під час зрівноваження обома способами. Зрівноважування завершують

складанням каталогу висот реперів і оцінкою точності отриманих результатів.

~>7

РОЗДІЛ II. ПЛАНОВІ ГЕОДЕЗИЧНІ МЕРЕЖІ

11.1. Методи створення планових мереж. Основні вимоги.

Формули

II.

1.1. Сучасні методи створення планових мереж

Планові опорні геодезичні мережі - це точки з відомими коорди-

натами (Х

У,), які фундаментально закріплені на земній поверхні або на

спорудах, і визначені на основі лінійних та кутових вимірів.

У залежності від геометричної форми та безпосередньо виміряних

елементів розрізняють чотири основні методи створення планових мереж:

1. Тріангуляція;

2. Полігонометрія;

3. Трилатерація;

4. Супутниковий метод.

Розглянемо суть кожного із цих методів.

1. Тріангуляція - це мережа трикутників, що межують один з одним,

у яких вимірюють усі кути й хоча би одну сторону. На рисунку II. 1.1 подано

ланку тріангуляції, що складається із восьми трикутників. Довжини сторін

трикутників у ланках тріангуляції можуть сягати 20-25 км.

Чотирикутник АМВИ - базисна мережа. Базисні мережі будувались

для визначення довжини сторони трикутника. Сторона АВ безпосередньо

не вимірювалась. Вимірювався базис - лінія МУ та вісім кутів чотирикут-

ника - ромба, що дістав назву геодезичного чотирикутника. У цьому

чотирикутнику більша діагональ АВ, що визначалась, одночасно є стороною

першого трикутника ланки. Базис вимірювався підвісними мірними

приладами. Такі сторони, як АВ, називають вихідними. Базисні мережі буду-

валися до появи світловіддалемірів. Світловідцалемірами можна вимірювати

довжини сторін трикутників, не будуючи базисних мереж. Сторони,

безпосередньо виміряні світловіддалемірами, називають базисними. Ланки

тріангуляції, зазвичай, складаються з 10-12 трикутників. Віддалі між

кінцевими пунктами ланки можуть сягати 200-250 км. Ланки, як правило,

прокладають уздовж меридіанів та паралелей. Чотири таких ланки (дві -

уздовж паралелей, дві - уздовж меридіанів) створюють полігон периметром

800-1000 км. Усередині полігон заповнюють суцільною мережею

трикутників тріангуляції такого ж класу, або нижчого за точністю. Вершини

трикутників, закріплені на місцевості, називають пунктами тріангуляції.

Координати початкових (вихідних) пунктів на кінцях ланки та азимути

вихідних сторін визначають з астрономічних спостережень. На таких

пунктах, показаних на рисунку п'ятикутними зірками, виконують астро-

номічні визначення широт <р та довгот X, а також визначення прямих та

зворотних азимутів сторін АВ та С£>. Такі пункти називають пунктами

Лапласа. Горизонтальні кути та довжини сторін визначають із геодезичних

вимірювань. Мережі, де поєднують астрономічні й геодезичні вимірювання,

називають астрономо-геодезичними.

Рис.

II.

1.1. Астрономо-геодезична тріангуляційна ланка.

У колишньому Радянському Союзі, у який входила Україна, була

створена державна тріангуляційна мережа, що складалася із чотирьох класів:

найточніший - 1-й клас, точність мереж поступово знижувалась з переходом

до 2-го, 3-го, та 4-го класів. Основні вимоги до державних тріангуляційних

мереж СРСР подані в таблиці

II.

1.1.

Таблиця

II. 1.1

Головні вимоги до мереж тріангуляції

колишньому СРСР.

——— Класи

Характеристики —

1 2

Довжини сторін трикутників, (км)

20-25 7-20 5-8

2-5

Відносні похибки визначення

базисних сторін

1:400000

1:300000 1:200000

1:100000

Середня квадратична похибка

вимірювання кутів, (")

±0,7

±1,0

±1,5 ±2,0

2. Трилатерація - це також ланки трикутників, як і в тріангуляції, що

межують один з одним, але з виміряними сторонами, а не кутами. Вершини

трикутників мережі трилатерації називають пунктами трилатерації. Кінцева

мета створення трилатерації, як і створення тріангуляції - визначення пла-

нових координат пунктів.

3. Полігонометрія - побудована на місцевості система ламаних ліній

(рис.

II.

1.2) з виміряними відрізками 8

та горизонтальними кутами Д,

Ламана лінія - це полігонометричний хід. Відрізки - сторони полігоно-

метричного ходу. Горизонтальні кути Д між відрізками - кути повороту

ходу; вершини полігонометричного ходу, позначені на рисунку кружками,

пронумеровані 1, 2, ..., /', ..., л+1 є пунктами полігонометричного ходу.

Пункти полігонометрії фундаментально закріплені на місцевості, як і пункти

тріангуляції чи трилатерації.

Ук

Рис.

II. 1.2.

Полігонометричний хід, прокладений між пунктами тріангуляції

(Т

- початковий, Т

- кінцевий) з відомими координатами і дирекційними

кутами.

Метод полігонометрії вважають рівноцінним із методом тріангуляції.

Тому і вимоги до мереж полігонометрії майже такі ж, як до мереж тріангу-

ляції. Ці вимоги подані в таблиці

II.

1.2. Як бачимо з таблиці, державна

полігонометрія

колишньому Радянському Союзі також мала чотири класи.

Таблиця

II. 1.2

Основні вимоги до державної полігонометрії в колишньому СРСР.

Класи

Характеристакіг-—

1 2 3

Довжина сторін, (км)

20-25

7-20

5-8 2-5

Відносна похибка

вимірювання сторін

1:300000 1:250000

1:200000*

(1:150000)

1:150000*

(1:100000)

Середня квадратична

похибка вимірювання

кутів, (")

0,4 1,0

1,5

2,0

* для сторін полігонометрії 3-го та 4-го класів, близьких до мінімальних,

допускають відносні похибки 1:150000 та 1:100000, відповідно.

Проте, до появи світловіддалемірів (світловіддалеміри в геодезично-

му виробництві з'явились тільки після 2-ї світової війни) тріангуляція

займала провідне місце, як метод створення державних геодезичних мереж.

Метод полігонометрії застосовувався значно менше, переважно через

складність вимірювання ліній.

4, Супутниковий метод створення мереж. У наш час поширене

застосування має система ОР8 - ОІоЬаІ РОЇІІІОПІП§ Зузїет (глобальна по-

шукова система). Розглянемо принцип визначення положення наземних

пунктів системою ОРЗ. 6Р8-приймач, що встановлюють на пункті, коорди-

ната якого визначають (пункт Р на рисунку

II.

1.3), приймає радіосигнали від

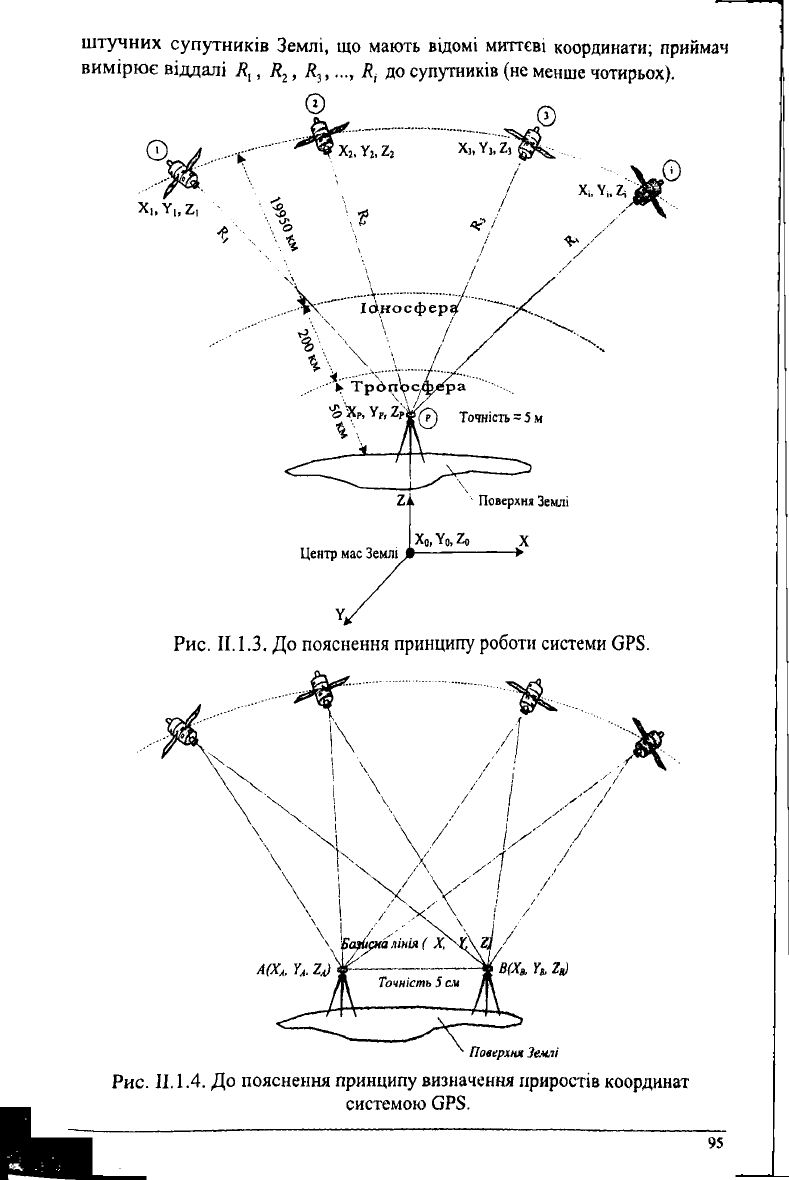
штучних супутників Землі, що мають відомі миттєві координати; приймач

вимірює віддалі Л,, Я

, ..., К, до супутників (не менше чотирьох).

с>

' Я,

^ \ 'Л

Хг, Уг, ї.%

Х,,У),2ц

....^Ч""*" Шносфер^

1 ...

••""

£ Тр6п'оа

Хр, Ур, 2р

Рис.

II.

1.3. До пояснення принципу роботи системи 0Р5.

\ !

' / /'

/X /

\ ! /

и/

\ І /

\ Баріріа

лінія

(

а (х

,у

л^— -^«йіігі)

Точність 5 см

Поверхня Землі

Рис. II. 1.4. До пояснення принципу визначення приростів координат

системою ОР8.

Координати супутників передаються на ОР8-приймач. У відповіднос-

ті з рис.

II. 1.4

можна записати чотири таких рівняння:

-2

)

-Х

)

+(У

-У

)

+(2

-2

)

-Х

)

+(Уз

~Г

)

+(2 з

-Х

)

(У

-Ур)

+(їг

-2

)

У системі

(II. 1.1)

три невідомі Х

, У

, 2

. Насправді, є чотири неві-

домі: крім Х

, Ї

, 2

ще невідома асинхронність 5

(різниця похибок

показників хронометрів супутника та приймача). Саме тому потрібно спос-

терігати мінімум чотири супутники. Розв'язавши ці рівняння, знайдемо

шукані координати точки Р. Електронно-обчислювальна система ОР8-прий-

мачарозв'язує ці рівняння і відображає на дисплеї координати Х

, У

, 2

ОР5-приймачі пристосовані до визначення прямокутних геодезичних

координат X, У, 2 (з початком в центрі мас Землі), топоцентричних

прямокутних координат X, У, Н (із початком координат на топографічній

поверхні землі) та геодезичних координат В, Ь, Н (широт, довгот та

висот). Визначення геоцентричних координат виконують з точністю до 5 м.

Така точність не задовольняє вимогам геодезії.

Якщо один ОР8-приймач знаходиться на пункті з відомими

координатами, а другий - на невідомому (рис. II. 1.4), тоді можна отримати

прирости координат ЬХ, ДУ, Д2. Такі відносні, а не абсолютні визначення

координат значно (приблизно в 100 разів) точніші. Похибка визначення

координат біля 5 см може бути зменшена збільшенням часу спостереження.

Як це зрозуміло з рисунку, ОРЗ-технології дозволяють одночасно

визначати як планове, так і висотне положення наземних пунктів. В геодезії

широке застосування набув відносний метод визначення координат.

11.1.2.

Основні положення створення планових державних

геодезичних мереж (ДГМ)

Основні положення затверджені Постановою Кабінету Міністрів

України від 8 червня 1998 р. № 844.

Планова геодезична мережа складається з:

• асірономо-геодезичиої мережі 1 класу;

• геодезичної мережі 2 класу;

• геодезичної мережі згущення 3 класу.

Для знімання масштабів 1:5000, 1:2000, 1:1000, 1:500 створюють

розрядні мережі згущення, які поділяють на:

• мережі полігонометрії, трилатерації і тріангуляції 4 класу;

• мережі полігонометрії, трилатерації і тріангуляції І і II розрядів.

ДГМ створюють для вирішення таких основних завдань країни в інте-

ресах господарської діяльності, науки та оборони країни:

• встановлення єдиної геодезичної системи координат країни;

• забезпечення вихідними геодезичними даними засобів наземної,

морської й аерокосмічної навігації;

• вивчення фігури і гравітаційного поля Землі та їх змін у часі;

• дослідження геодинамічних явищ та рухів земної поверхні;

• обґрунтування регіонів пошуку корисних копалин;

• вивчення руху полюсів та нерівномірності обертання Землі;

• інші задачі.

Положення пунктів ДГМ визначають у двох системах координат -

загальноземній та референцній; між ними встановлюється однозначний зв'я-

зок, який визначають параметрами взаємного переходу. За загальноземну

систему приймають геодезичну референцну систему 1980-го року (СРЗ

1980) з такими параметрами еліпсоїда:

велика піввісь а = 6378137 м, стиснення е = = —-— (Ь - мала

а 298,257

піввісь).

На перехідний період (до введення системи ОР8) залишається

система координат 1942 року (СК-42) з вихідними даними:

• референц-еліпсоїд Красовського (велика піввісь а = 6378245 м);

• стиснення 1:298,3;

• висота геоїда в Пулково над референц-еліпсоїдом дорівнює нулю.

11.1.3. Астрономо-геодезична мережа 1 класу (АГМ-1)

Астрономо-геодезичну мережу будують у вигляді однорідної за

точністю просторової геодезичної мережі, яка складається із системи

рівномірно розташованих геодезичних пунктів, віддалених один від одного

на 50-150 км. АГМ-1 є геодезичною основою для побудови нових мереж і

забезпечення подальшого підвищення точності існуючої мережі.

Частина пунктів АГМ-1 представляє собою постійно діючі станції

ОР5 спостережень та астрономо-геодезичні обсерваторії, на яких виконують

комплекс безперервних супутникових астрономо-геодезичних, гравіметрич-

них та геофізичних спостережень за змінами форми і розмірів Землі, її

гравітаційного поля, викликаними геодинамічними процесами.

Решта пунктів АГМ-1 - це фундаментально закріплені на місцевості

пункти, положення яких періодично визначають в рамках довгострокової

програми їх функціонування.

Систему координат АГМ-1 узгоджують з науковими проектами між-

народного співробітництва. Просторове положення пунктів АГМ-1 виз-

начають методами супутникової геодезії в загально-земній системі з віднос-

ною похибкою Др/р = 1 • 10"

(До - середня квадратична похибка ВИЗНа-

оч

чення геоцентричного радіуса р пункту). Кожен пункт АГМ-1 повинен бути

зв'язаний ОР8 вимірюваннями не менш як з трьома пунктами мережі, які

межують з ним.

Пункти АГМ-1 повинні бути зв'язані з мережами високоточного ніве-

лювання, що дозволяє визначити перевищення нормальних висот між сусід,

німи пунктами АГМ-1 з середньоквадратичними похибками не більшими за

0,05 метрів. На кожному пункті АГМ-1 періодично повторюють визначення

відхилення прямовисних ліній із середньоквадратичною похибкою - 0,5".

11.1.4.

Основні вимоги до державної мережі 2 класу

Геодезичну мережу 2 класу будують у вигляді однорідної за точністю

просторової мережі, яка складається з рівномірно розташованих пунктів

мережі 1 та 2 класів, побудованих згідно з вимогами до такої мережі в

колишньому СРСР та нових пунктів, що визначаються відповідно до вимог

сучасній основних положень. Нові пункти геодезичної мережі 2 класу

розташовуються на відстані 8-12 км, і їх положення визначають, як правило,

відповідними методами супутникової геодезії, а також наземними методами

{тріангуляції, трилатерації, полігонометрії), які забезпечують точність

визначення взаємного положення пунктів з середньоквадратичними похиб-

ками 0,03-0,05 метрів для середньої довжини сторін 10 км. За вихідні пункти

приймають пункти АГМ-1. Група нових пунктів мережі 2 класу повинна

мати зв'язок не менш ніж із трьома пунктами АГМ-1. Периметр полігонів

полігонометрії 150-180 км, найбільша довжина полігонометричного ходу 60

км. Основні вимоги до побудови мережі 2 класу подані в таблиці 11.1.3.

Таблиця 11,1.3

Основні вимога до побудови геодезичних мереж 2 класу.

Параметри мережі

ОР5

тріангуляція

полігоно-

метрія

трилатера-

ція

Довжини найбільша

сторін,

(км)

найменша

Середня квадратична

похибка вимірювання

куга, не більше, (")

Відносна похибка

вимірювання сторін

(базису), т

І5

1:300000

Середня квадратична

похибка вимірюван-

ня сторони, не

більше, (м)

0,03

11.1.5. Основні вимоги до державної мережі згущення 3 класу

Геодезичну мережу згущення 3 класу будують з метою збільшення

кількості пунктів до щільності, яка забезпечує створення знімальної основи

великомасштабного топографічного та кадастрового знімання. Вола вклю-

чає геодезичні мережі згущення 3 та 4 класів, побудованих згідно з вимо-

гами положення про державну геодезичну мережу СРСР 1954-61 років, та

нові мережі згущення, що будують згідно сучасних Основних положень.

Нові пункти геодезичної мережі згущення 3 класу визначають одним

із чотирьох раніше перерахованих методів. Вихідними служать пункти

АГМ-1 та геодезичні мережі 2 класу (ГМ-2).

Якщо мережі згущення 3 класу будують методом полігонометрії, тоді

прокладають поодинокі ходи або ходи з вузловими точками, які опираються

на пункти більш високого класу. Периметри полігонів полігонометрії 70-90

км; найбільша довжина ходу складає

ЗО

км. Якщо відстані між пунктами, що

належать до різних ходів, менші за 2 км, ці ходи обов'язково з'єднують

додатковими ходами. По можливості повинна забезпечуватися видимість

(земля-земля) між суміжними пунктами мережі. За відсутності видимості

закладають два орієнтирних пункти.

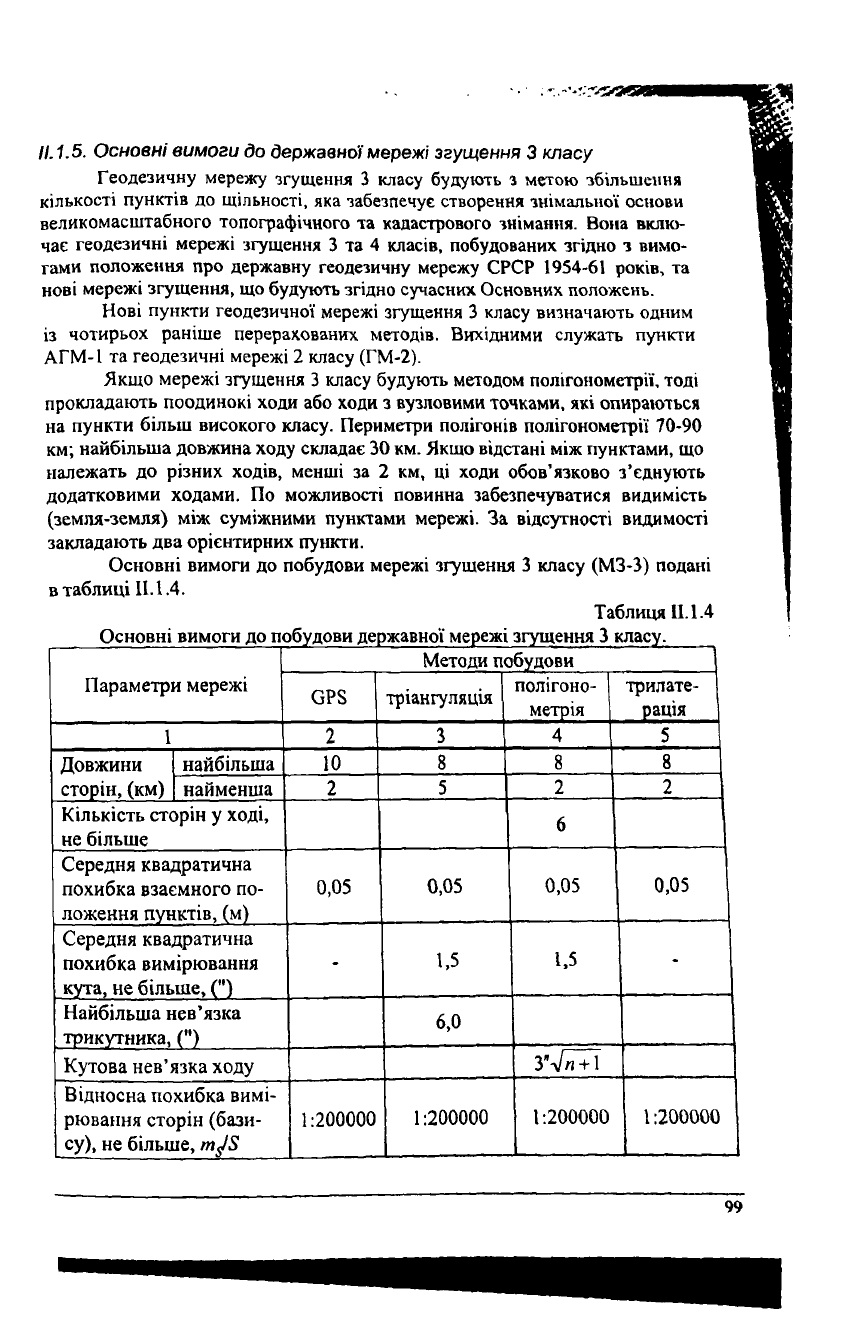
Основні вимоги до побудови мережі згущення 3 класу (МЗ-З) подані

в таблиці

II.

1.4.

Таблиця 11.1.4

Основні вимоги до побудови державної мережі згущення 3 класу.

Методи побудови

Параметри мережі

ОРЗ

тріангуляція

полігоно- 1

метрія 1

трилате-

рація

1 2

4 5

Довжини

найбільша

сторін, (км) найменша

2 2

Кількість сторін у ході,

не більше

Середня квадратична

похибка взаємного по-

0,05

ложення пунктів, (м)

Середня квадратична

похибка вимірювання

кута, не більше, (")

- 1,5

1,5

Найбільша нев'язка

трикутника, (")

6,0

Кутова нев'язка ходу

З'л/л +

Відносна похибка вимі-

рювання сторін (бази-

су), не більше, т^3

1:200000

1:200000 1:200000

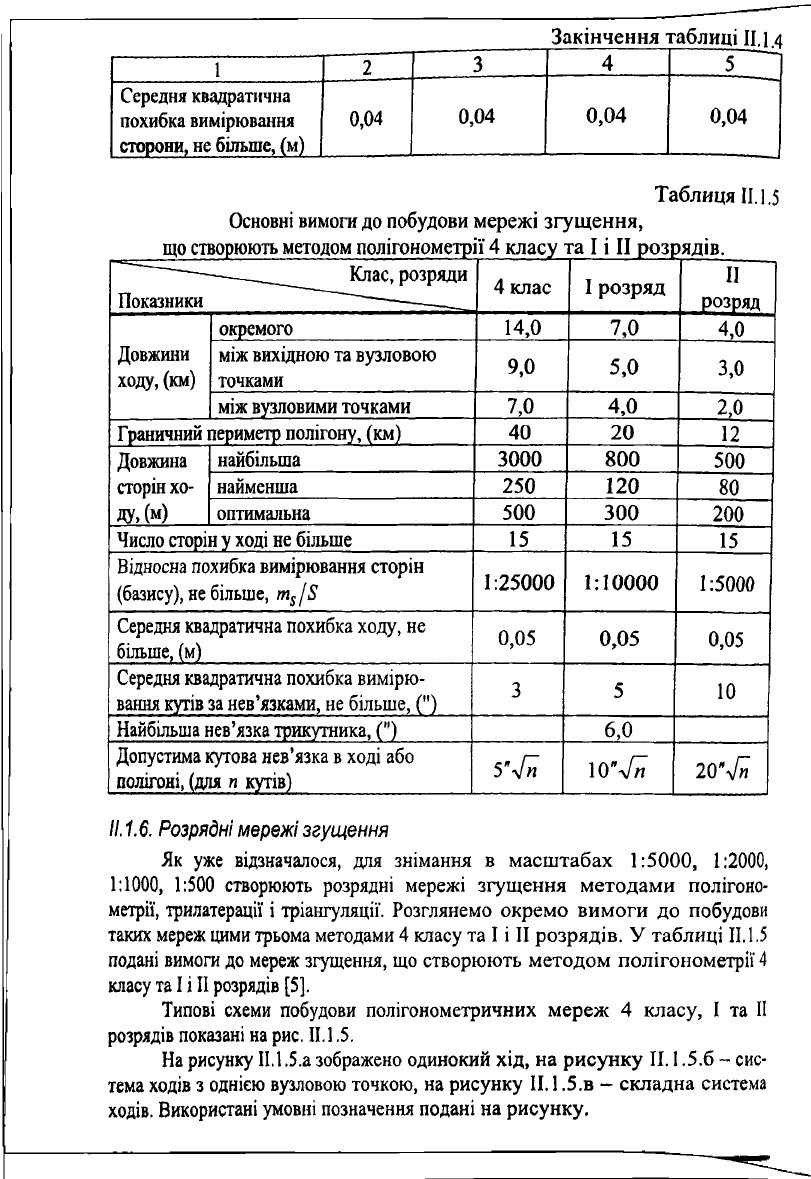
Закінчення таблиці

II. і

Середня квадратична

0,04

похибка вимірювання

0,04

0,04 0,04

0,04

сторони, не більше, (м)

Таблиця

II. 1.5

Основні вимоги до побудови мережі згущення,

що створюють методом полігонометрії 4 класу та І і II розрядів.

—•——__ Клас, розряди

Показники _____

4 клас

І розряд

розряд

Довжини

ходу, (км)

окремого

14,0

7,0

4,0

Довжини

ходу, (км)

між вихідною та вузловою

точками

9,0

5,0

3,0

Довжини

ходу, (км)

між вузловими точками 7,0

4,0

2,0

Граничний периметр полігону, (км)

Довжина

сторін хо-

ДУ,

(м)

найбільша

3000 800

500

Довжина

сторін хо-

ДУ,

(м)

найменша

250 120

Довжина

сторін хо-

ДУ,

(м)

оптимальна

500

300

200

Число сторін у ході не більше

15 15

Відносна похибка вимірювання сторін

(базису), не більше, т

1:25000 1:10000

1:5000

Середня квадратична похибка ходу, не

більше, (м)

0,05

Середня квадратична похибка вимірю-

вання кутів за нев'язками, не більше, (")

Найбільша нев'язка трикутника, (")

6,0

Допустима кутова нев'язка в ході або

полігоні, (для п кутів)

Ю'Ч/Й

20"л/«

11.1.6.

Розрядні мережі згущення

Як уже відзначалося, для знімання в масштабах 1:50 00, 1:2000,

1:1000, 1:500 створюють розрядні мережі згущення методами полігоно-

метрії, трилатерації і тріангуляції. Розглянемо окремо вимоги до побудови

таких мереж цими трьома методами 4 класу та І і II розрядів. У таблиці

II. 1.5

подані вимоги до мереж згущення, що створюють методом полігонометрії 4

класу та

і II розрядів [5].

Типові схеми побудови полігонометричних мереж 4 класу, І та II

розрядів показані на рис.

II.

1.5.

На рисунку

II.

1.5.а зображено одинокий хід, на рисунку II. 1.5.6 - сис-

тема ходів з однією вузловою точкою, на рисунку II. 1.5.в - складна система

ходів. Використані умовні позначення подані на рисунку.