Носко В.П. Эконометрика для начинающих
Подождите немного. Документ загружается.

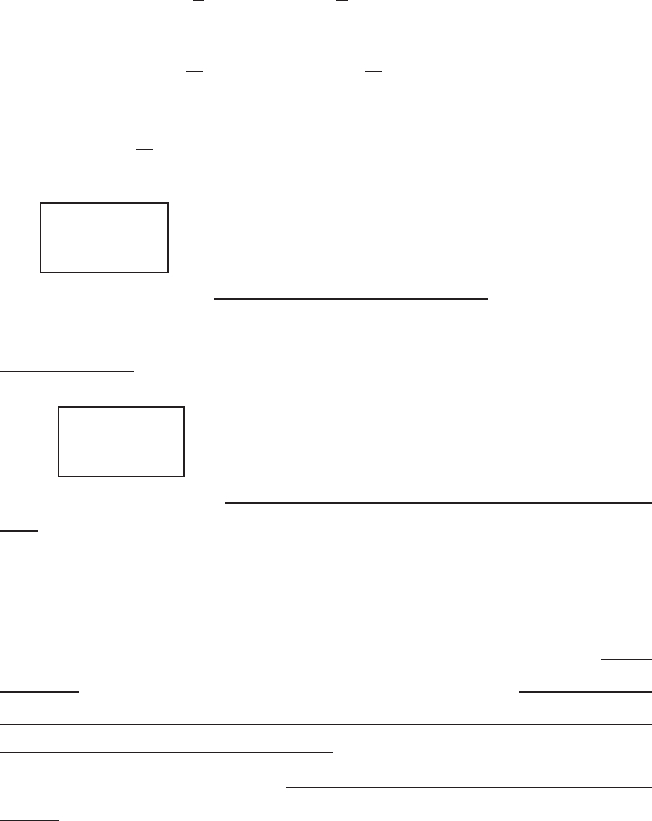
15
E
¦¦¦
¦¦¦ ¦
wy y wy y w
wy w y w wy cy
i
i
n
ii
i
n
ii
i
n
i
i
n
ii
i
n
i
i
n
ii
i
n
i
111
111 1
,
ɝɞɟ
cww
ii
.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ,
E
¦
cy
i
i
n
i
1
,
ɝɞɟ
cc
n1
,, — ɮɢɤɫɢɪɨɜɚɧɧɵɟ ɜɟɥɢɱɢɧɵ, ɚ yy
n1
,, —
ɧɚɛɥɸɞɚɟɦɵɟ ɡɧɚɱɟɧɢɹ ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ
YY
n1
,, . ɉɨɷɬɨɦɭ
ɜɵɱɢɫɥɟɧɧɨɟ
ɩɨ ɩɨɫɥɟɞɧɟɣ ɮɨɪɦɭɥɟ ɡɧɚɱɟɧɢɟ
E
ɹɜɥɹɟɬɫɹ
ɧɚ-
ɛɥɸɞɚɟɦɵɦ ɡɧɚɱɟɧɢɟɦ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ
E
¦
cY
i
i
n
i
1
,
ɤɨɬɨɪɚɹ ɹɜɥɹɟɬɫɹ ɥɢɧɟɣɧɨɣ ɤɨɦɛɢɧɚɰɢɟɣ ɫɥɭɱɚɣɧɵɯ ɜɟɥɢ-
ɱɢɧ YY
n1
,, ɢ ɢɦɟɟɬ ɧɟɤɨɬɨɪɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɜɟɪɨɹɬɧɨɫɬɟɣ,
ɡɚɜɢɫɹɳɟɟ ɨɬ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɩɨɫɥɟɞɧɢɯ.
ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ, ɚɧɚɥɢɬɢɱɟɫɤɨɟ ɨɩɢɫɚɧɢɟ ɪɚɫɩɪɟɞɟɥɟɧɢɹ
E
ɤɚɤ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɞɨɜɨɥɶɧɨ ɡɚɬɪɭɞɧɢɬɟɥɶɧɨ. Ȼɨɥɟɟ
ɩɪɨɫɬɨ ɷɬɚ ɡɚɞɚɱɚ ɪɟɲɚɟɬɫɹ ɜ ɫɢɬɭɚɰɢɢ, ɤɨɝɞɚ
H
i
ɢɦɟɟɬ ɝɚɭɫ-
ɫɨɜɫɤɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ. ȿɫɥɢ ɨɲɢɛɤɢ
H
H
1
,,
n
- ɧɟɡɚɜɢɫɢɦɵɟ
ɫɥɭɱɚɣɧɵɟ ɜɟɥɢɱɢɧɵ, ɢɦɟɸɳɢɟ ɨɞɢɧɚɤɨɜɨɟ ɧɨɪɦɚɥɶɧɨɟ ɪɚɫ-
ɩɪɟɞɟɥɟɧɢɟ ɫ ɧɭɥɟɜɵɦ ɫɪɟɞɧɢɦ, ɬɨ ɬɨɝɞɚ ɨɰɟɧɤɚ ɧɚɢɦɟɧɶɲɢɯ
ɤɜɚɞɪɚɬɨɜ
E
ɩɚɪɚɦɟɬɪɚ
E
ɬɚɤɠɟ ɢɦɟɟɬ ɧɨɪɦɚɥɶɧɨɟ ɪɚɫɩɪɟɞɟ-
ɥɟɧɢɟ. ɑɬɨɛɵ ɭɤɚɡɚɬɶ ɩɚɪɚɦɟɬɪɵ ɷɬɨɝɨ ɧɨɪɦɚɥɶɧɨɝɨ ɪɚɫɩɪɟɞɟ-
ɥɟɧɢɹ ɢ ɢɦɟɬɶ ɜɨɡɦɨɠɧɨɫɬɶ ɩɪɨɜɨɞɢɬɶ ɫɬɚɬɢɫɬɢɱɟɫɤɢɣ ɚɧɚɥɢɡ
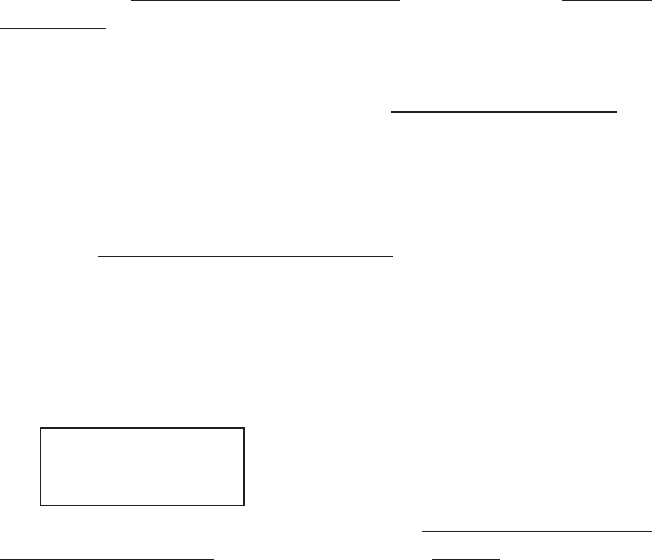
16
ɩɨɞɨɛɪɚɧɧɨɣ ɦɨɞɟɥɢ ɥɢɧɟɣɧɨɣ ɫɜɹɡɢ ɦɟɠɞɭ ɩɟɪɟɦɟɧɧɵɦɢ
ɮɚɤɬɨɪɚɦɢ, ɧɚɦ ɩɪɢɞɟɬɫɹ ɭɞɟɥɢɬɶ ɜɧɢɦɚɧɢɟ ɧɟɤɨɬɨɪɵɦ ɜɚɠ-
ɧɵɦ ɱɢɫɥɨɜɵɦ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚɦ ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ ɢ ɢɯ
ɫɜɨɣɫɬɜɚɦ.
2.3. ɑɂɋɅɈȼɕȿ ɏȺɊȺɄɌȿɊɂɋɌɂɄɂ ɋɅɍɑȺɃɇɕɏ
ȼȿɅɂɑɂɇ ɂ ɂɏ ɋȼɈɃɋɌȼȺ
ɋɥɭɱɚɣɧɵɟ ɜɟɥɢɱɢɧɵ, ɫ ɤɨɬɨɪɵɦɢ ɦɵ ɢɦɟɟɦ ɞɟɥɨ ɜ ɞɚɧ-
ɧɨɦ ɤɭɪɫɟ, ɩɨɥɧɨɫɬɶɸ ɨɩɪɟɞɟɥɹɸɬɫɹ
ɡɚɞɚɧɢɟɦ ɢɯ ɮɭɧɤɰɢɢ
ɩɥɨɬɧɨɫɬɢ, ɭɤɚɡɵɜɚɸɳɟɣ ɧɚ ɡɨɧɵ ɛɨɥɟɟ ɜɟɪɨɹɬɧɵɯ ɢ ɦɟɧɟɟ ɜɟ-
ɪɨɹɬɧɵɯ ɡɧɚɱɟɧɢɣ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ. ɑɚɫɬɨ, ɨɞɧɚɤɨ, ɢɧɬɟ-
ɪɟɫɭɸɬɫɹ ɛɨɥɟɟ ɫɠɚɬɵɦɢ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚɦɢ ɪɚɫɩɪɟɞɟɥɟɧɢɣ
ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ, ɜɵɪɚɠɟɧɧɵɦɢ ɨɬɞɟɥɶɧɵɦɢ ɱɢɫɥɚɦɢ
. Ʉ
ɬɚɤɢɦ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚɦ, ɜ ɩɟɪɜɭɸ ɨɱɟɪɟɞɶ, ɨɬɧɨɫɹɬɫɹ
ɦɚɬɟ-
ɦɚɬɢɱɟɫɤɨɟ ɨɠɢɞɚɧɢɟ
ɢ
ɞɢɫɩɟɪɫɢɹ
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ.
ɉɭɫɬɶ ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ
X
ɢɦɟɟɬ ɮɭɧɤɰɢɸ ɩɥɨɬɧɨɫɬɢ
p
x
(). Ƚɪɚɮɢɤ ɮɭɧɤɰɢɢ
p
x
() ɨɝɪɚɧɢɱɢɜɚɟɬ ɜɦɟɫɬɟ ɫ ɨɫɶɸ ɚɛɫ-
ɰɢɫɫ Ox ɩɨɥɨɫɭ ɩɟɪɟɦɟɧɧɨɣ ɲɢɪɢɧɵ
. ȿɫɥɢ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɷɬɭ
ɩɨɥɨɫɭ ɤɚɤ ɦɚɬɟɪɢɚɥɶɧɵɣ ɨɛɴɟɤɬ ɨɩɪɟɞɟɥɟɧɧɨɣ (ɩɨɫɬɨɹɧɧɨɣ)
ɬɨɥɳɢɧɵ, ɢɡɝɨɬɨɜɥɟɧɧɵɣ ɢɡ ɨɞɧɨɪɨɞɧɨɝɨ ɦɚɬɟɪɢɚɥɚ ɢ ɢɦɟɸ-
ɳɢɣ ɦɚɫɫɭ, ɪɚɜɧɭɸ ɟɞɢɧɢɰɟ, ɬɨ ɚɛɫɰɢɫɫɚ ɰɟɧɬɪɚ ɬɹɠɟɫɬɢ ɷɬɨɝɨ
ɦɚɬɟɪɢɚɥɶɧɨɝɨ ɨɛɴɟɤɬɚ ɧɚɡɵɜɚɟɬɫɹ
ɦɚɬɟɦɚɬɢɱɟɫɤɢɦ ɨɠɢɞɚ-
ɧɢɟɦ
(
expectation
)
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ X
, ɨɛɨɡɧɚɱɚɟɬɫɹ
E (X)
ɢ ɜɵɱɢɫɥɹɟɬɫɹ ɩɨ ɮɨɪɦɭɥɟ
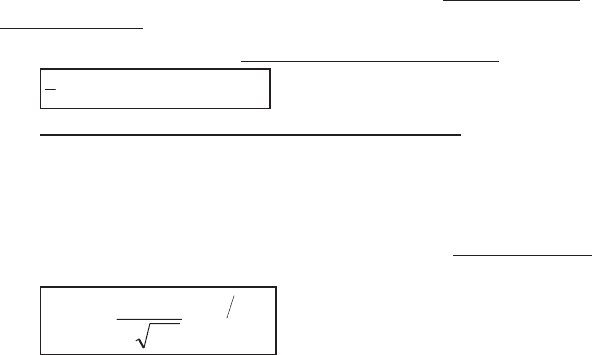
EX xpxdx() ()
f
f
³
.
ȿɫɥɢ ɝɪɚɮɢɤ ɮɭɧɤɰɢɢ ɩɥɨɬɧɨɫɬɢ ɫɢɦɦɟɬɪɢɱɟɧ ɨɬɧɨɫɢ-
ɬɟɥɶɧɨ ɨɫɢ ɨɪɞɢɧɚɬ (ɬɚɤ ɱɬɨ
p
x
() — ɱɟɬɧɚɹ ɮɭɧɤɰɢɹ), ɬɨ
E
X
() 0.
17
Ⱦɨɜɨɥɶɧɨ ɱɚɫɬɨ ɨ
E
X
() ɝɨɜɨɪɹɬ ɤɚɤ ɨ
ɫɪɟɞɧɟɦ ɡɧɚɱɟɧɢɢ
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ X
. ɗɬɨ ɫɜɹɡɚɧɨ ɫ ɬɟɦ, ɱɬɨ ɟɫɥɢ
XX
n1
,,
—
ɧɟɡɚɜɢɫɢɦɵɟ ɤɨɩɢɢ
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ
X
(ɬ. ɟ. ɫɥɭɱɚɣ-
ɧɵɟ ɜɟɥɢɱɢɧɵ
XX
n1
,,
ɧɟɡɚɜɢɫɢɦɵ ɜ ɫɨɜɨɤɭɩɧɨɫɬɢ ɢ ɢɦɟɸɬ
ɬɨ ɠɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ, ɱɬɨ ɢ
X
), ɬɨ ɬɨɝɞɚ ɩɪɢ ɛɨɥɶɲɢɯ n ɞɥɹ
ɧɚɛɥɸɞɚɟɦɵɯ
ɡɧɚɱɟɧɢɣ xx
n1
,, ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ
XX
n1
,,
ɢɦɟɟɬ ɦɟɫɬɨ ɩɪɢɛɥɢɠɟɧɧɨɟ ɪɚɜɟɧɫɬɜɨ
1
1
n
n
xxEX # () ,
ɬɟɦ ɛɨɥɟɟ ɬɨɱɧɨɟ, ɱɟɦ ɛɨɥɶɲɟ ɡɧɚɱɟɧɢɟ
n . ɂɧɵɦɢ ɫɥɨɜɚ-
ɦɢ, ɫ ɭɜɟɥɢɱɟɧɢɟɦ
n ɡɧɚɱɟɧɢɟ
E
X
() ɫɤɨɥɶ ɭɝɨɞɧɨ ɬɨɱɧɨ ɩɪɢ-
ɛɥɢɠɚɟɬɫɹ ɡɧɚɱɟɧɢɟɦ ɫɪɟɞɧɟɚɪɢɮɦɟɬɢɱɟɫɤɨɝɨ ɧɚɛɥɸɞɚɟɦɵɯ
ɜɟɥɢɱɢɧ
xx
n1
,,
.
Ɉɛɪɚɬɢɦɫɹ ɨɩɹɬɶ ɤ ɭɩɨɦɹɧɭɬɨɦɭ ɪɚɧɟɟ ɝɚɭɫɫɨɜɫɤɨɦɭ
(ɧɨɪ-
ɦɚɥɶɧɨɦɭ) ɪɚɫɩɪɟɞɟɥɟɧɢɸ ɫ ɮɭɧɤɰɢɟɣ ɩɥɨɬɧɨɫɬɢ
px e
x
()
1
2
22
2
VS
V
ɢ ɩɭɫɬɶ ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ
X
1
ɢɦɟɟɬ ɬɚɤɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ
ɫ
V
1
, ɚ ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ X
2
ɢɦɟɟɬ ɬɚɤɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ
ɫ
V
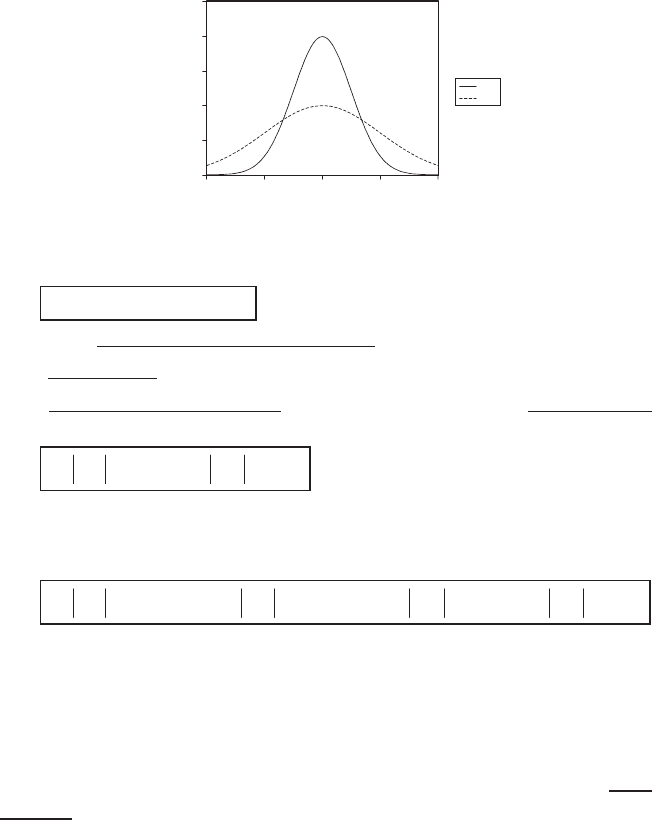
2 . ɋɪɚɜɧɢɦ ɝɪɚɮɢɤɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɮɭɧɤɰɢɣ ɩɥɨɬɧɨ-
ɫɬɢ (ɫɩɥɨɲɧɨɣ ɥɢɧɢɟɣ ɩɪɟɞɫɬɚɜɥɟɧ ɝɪɚɮɢɤ ɮɭɧɤɰɢɢ ɩɥɨɬɧɨɫɬɢ
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ
X
1
):
18
0.0
0.1
0.2
0.3
0.4
0.5
-4 -2 0 2 4
X
P_1
P_2
ɉɨɫɤɨɥɶɤɭ ɜ ɨɛɨɢɯ ɫɥɭɱɚɹɯ ɝɪɚɮɢɤɢ ɫɢɦɦɟɬɪɢɱɧɵ ɨɬɧɨɫɢ-
ɬɟɥɶɧɨ ɧɭɥɹ, ɬɨ
EX EX() ()
12
0 ,
ɬ. ɟ. ɦɚɬɟɦɚɬɢɱɟɫɤɢɟ ɨɠɢɞɚɧɢɹ
ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ
X
1
ɢ
X
2
ɫɨɜɩɚɞɚɸɬ. Ɉɞɧɚɤɨ, ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ
X
2
ɛɨɥɟɟ ɪɚɫɫɪɟɞɨɬɨɱɟɧɨ, ɢ ɷɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɞɥɹ ɥɸɛɨɝɨ
a ! 0
^`^`
PX a PX a
12
! ! .
ɉɪɢ ɷɬɨɦ ɝɨɜɨɪɹɬ, ɱɬɨ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢ-
ɧɵ
X
2
ɢɦɟɟɬ
ɛɨɥɟɟ ɬɹɠɟɥɵɟ
(
heavy
), ɢɥɢ
ɛɨɥɟɟ ɞɥɢɧɧɵɟ
(
long
)
ɯɜɨɫɬɵ
(
tails
). ɋɨɨɬɜɟɬɫɬɜɟɧɧɨ,
^`^`^`^`
PX a PX a PX a PX a
1122
11d !! ! d .
ȼ ɪɚɫɫɦɨɬɪɟɧɧɨɦ ɫɥɭɱɚɟ ɜ ɤɚɱɟɫɬɜɟ ɱɢɫɥɨɜɨɣ ɯɚɪɚɤɬɟɪɢ-
ɫɬɢɤɢ ɫɬɟɩɟɧɢ ɪɚɫɫɪɟɞɨɬɨɱɟɧɧɨɫɬɢ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɦɨɠɧɨ ɛɵɥɨ
ɛɵ ɩɪɢɧɹɬɶ ɩɚɪɚɦɟɬɪ
V
: ɱɟɦ ɛɨɥɶɲɟ ɡɧɚɱɟɧɢɟ ɷɬɨɝɨ ɩɚɪɚɦɟɬɪɚ,
ɬɟɦ ɛɨɥɟɟ ɪɚɫɫɪɟɞɨɬɨɱɟɧɨ ɪɚɫɩɪɟɞɟɥɟɧɢɟ. ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ,
ɫɪɚɜɧɢɜɚɬɶ ɫɬɟɩɟɧɢ ɪɚɫɫɪɟɞɨɬɨɱɟɧɧɨɫɬɢ ɪɚɫɩɪɟɞɟɥɟɧɢɣ ɫɥɭ-
ɱɚɣɧɵɯ ɜɟɥɢɱɢɧ ɦɨɠɧɨ, ɩɪɢɜɥɟɤɚɹ ɞɥɹ ɷɬɨɣ ɰɟɥɢ ɩɨɧɹɬɢɟ ɞɢɫ-
ɩɟɪɫɢɢ.
Ⱦɢɫɩɟɪɫɢɟɣ
(
variance
)
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ X
ɧɚɡɵɜɚɸɬ
ɱɢɫɥɨ
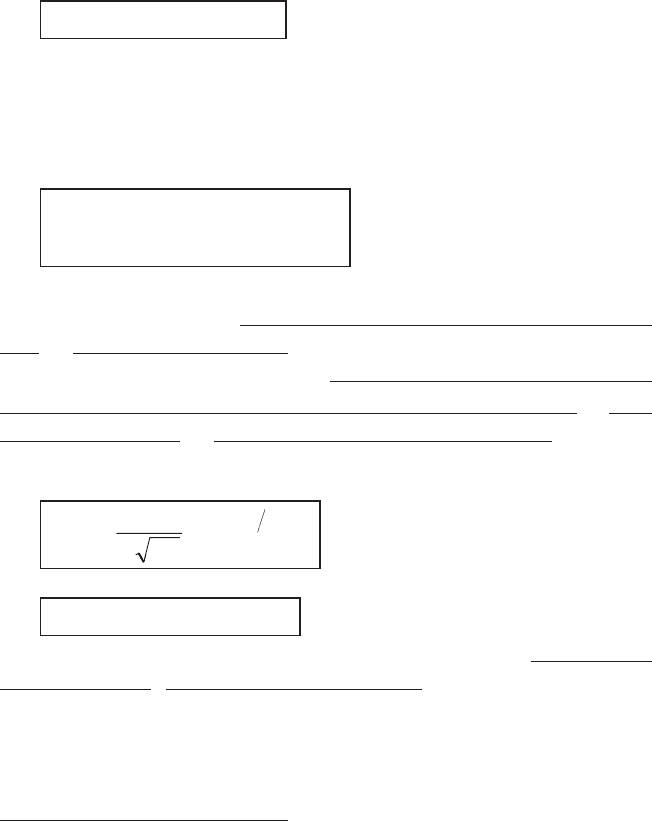
19
DX EX EX() ( ()),
2
ɪɚɜɧɨɟ ɦɚɬɟɦɚɬɢɱɟɫɤɨɦɭ ɨɠɢɞɚɧɢɸ ɤɜɚɞɪɚɬɚ ɨɬɤɥɨɧɟɧɢɹ
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ
X
ɨɬ ɟɟ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɨɠɢɞɚɧɢɹ
E
X
().
1
Ɂɧɚɹ ɮɭɧɤɰɢɸ ɩɥɨɬɧɨɫɬɢ
p
x
() ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ
X
, ɞɢɫ-
ɩɟɪɫɢɸ ɷɬɨɣ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɦɨɠɧɨ ɜɵɱɢɫɥɢɬɶ ɩɨ ɮɨɪ-
ɦɭɥɟ
DX x EX pxdx() () ()
f
f
³
2
.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɦɚɬɟɦɚɬɢɱɟɫɤɨɟ ɨɠɢɞɚɧɢɟ
E
X
()ɦɨɠɧɨ
ɢɧɬɟɪɩɪɟɬɢɪɨɜɚɬɶ ɤɚɤ ɜɡɜɟɲɟɧɧɨɟ ɫɪɟɞɧɟɟ ɜɨɡɦɨɠɧɵɯ ɡɧɚɱɟ-
ɧɢɣ
x
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ
X
, ɫ ɜɟɫɚɦɢ, ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɵɦɢ
p
x
(), ɚ ɞɢɫɩɟɪɫɢɸ D
X
()— ɤɚɤ ɜɡɜɟɲɟɧɧɨɟ ɫɪɟɞɧɟɟ (ɫ ɬɟɦɢ ɠɟ
ɜɟɫɚɦɢ) ɤɜɚɞɪɚɬɨɜ ɨɬɤɥɨɧɟɧɢɣ ɜɨɡɦɨɠɧɵɯ ɡɧɚɱɟɧɢɣ
x
ɫɥɭ-
ɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ
X
ɨɬ ɟɟ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɨɠɢɞɚɧɢɹ.
ȿɫɥɢ ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ
X
ɢɦɟɟɬ
ɧɨɪɦɚɥɶɧɨɟ ɪɚɫɩɪɟɞɟ-
ɥɟɧɢɟ
ɫ ɮɭɧɤɰɢɟɣ ɩɥɨɬɧɨɫɬɢ
px e
x
()
1
2
2
2
2
VS
PV
,
ɬɨ ɞɥɹ ɧɟɟ
EX DX() ()
PV
, .
2
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ, ɢɦɟɸɳɚɹ ɧɨɪɦɚɥɶɧɨɟ
ɪɚɫɩɪɟɞɟɥɟɧɢɟ, ɩɨɥɧɨɫɬɶɸ ɨɩɪɟɞɟɥɹɟɬɫɹ (ɜ ɨɬɧɨɲɟɧɢɢ ɟɟ ɪɚɫ-
ɩɪɟɞɟɥɟɧɢɹ) ɡɚɞɚɧɢɟɦ ɡɧɚɱɟɧɢɣ ɟɟ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɨɠɢɞɚɧɢɹ
ɢ ɞɢɫɩɟɪɫɢɢ.
ȼ ɫɜɹɡɢ ɫ ɱɚɫɬɵɦ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ ɧɨɪɦɚɥɶɧɨ ɪɚɫɩɪɟɞɟɥɟɧ-
ɧɵɯ ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ ɜ ɞɚɥɶɧɟɣɲɟɦ ɢɡɥɨɠɟɧɢɢ, ɦɵ ɛɭɞɟɦ
1
ȼ ɥɢɬɟɪɚɬɭɪɟ ɩɨ ɷɤɨɧɨɦɟɬɪɢɤɟ ɦɚɬɟɦɚɬɢɱɟɫɤɨɟ ɨɠɢɞɚɧɢɟ ɫɥɭɱɚɣɧɨɣ
ɜɟɥɢɱɢɧɵ X ɨɛɨɡɧɚɱɚɸɬ ɢɧɨɝɞɚ ɫɢɦɜɨɥɨɦ M(X), ɚ ɞɥɹ ɞɢɫɩɟɪɫɢɢ ɫɥɭɱɚɣ-
ɧɨɣ ɜɟɥɢɱɢɧɵ X ɢɫɩɨɥɶɡɭɸɬ ɬɚɤɠɟ ɨɛɨɡɧɚɱɟɧɢɹ Var(X) ɢ V(X).
20
ɨɛɨɡɧɚɱɚɬɶ ɧɨɪɦɚɥɶɧɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ, ɢɦɟɸɳɟɟ ɦɚɬɟɦɚɬɢɱɟ-
ɫɤɨɟ ɨɠɢɞɚɧɢɟ
P
ɢ ɞɢɫɩɟɪɫɢɸ
V
2
, ɫɢɦɜɨɥɨɦ N (, )
PV
2
. ȼɫɥɭ-
ɱɚɟ, ɤɨɝɞɚ
P
0,
V
2
1 , ɝɨɜɨɪɹɬ ɨ
ɫɬɚɧɞɚɪɬɧɨɦ ɧɨɪɦɚɥɶɧɨɦ
ɪɚɫɩɪɟɞɟɥɟɧɢɢ
N
(,)01 . ɂɦɟɸɬɫɹ ɜɟɫɶɦɚ ɩɨɞɪɨɛɧɵɟ ɬɚɛɥɢɰɵ
ɡɧɚɱɟɧɢɣ ɮɭɧɤɰɢɢ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɢ ɮɭɧɤɰɢɢ ɩɥɨɬɧɨɫɬɢ ɫɬɚɧ-
ɞɚɪɬɧɨɝɨ ɧɨɪɦɚɥɶɧɨɝɨ ɪɚɫɩɪɟɞɟɥɟɧɢɹ.
Ⱦɥɹ ɞɚɥɶɧɟɣɲɟɝɨ ɧɚɦ, ɜ ɩɟɪɜɭɸ ɨɱɟɪɟɞɶ, ɩɨɧɚɞɨɛɹɬɫɹ ɫɥɟ-
ɞɭɸɳɢɟ ɩɪɨɫɬɵɟ
ɫɜɨɣɫɬɜɚ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɨɠɢɞɚɧɢɹ ɢ
ɞɢɫɩɟɪɫɢɢ
.
ȿɫɥɢ
a
- ɧɟɤɨɬɨɪɚɹ ɩɨɫɬɨɹɧɧɚɹ, ɨɬɥɢɱɧɚɹ ɨɬ ɧɭɥɹ, ɚ
X
- ɧɟ-
ɤɨɬɨɪɚɹ ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ
, ɬɨ ɬɨɝɞɚ ɫɭɦɦɚ
X
a ɢ ɩɪɨɢɡɜɟ-
ɞɟɧɢɟ aX ɬɚɤɠɟ ɹɜɥɹɸɬɫɹ ɫɥɭɱɚɣɧɵɦɢ ɜɟɥɢɱɢɧɚɦɢ; ɩɪɢ ɷɬɨɦ,
E
X
a
E
X
a
EaX aE X
()()
() ()
D
X
aD
X
DaX a D X
()()
() ().
2
Ⱦɜɚ ɫɜɨɣɫɬɜɚ, ɤɚɫɚɸɳɢɟɫɹ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɨɠɢɞɚɧɢɹ, ɧɟ-
ɩɨɫɪɟɞɫɬɜɟɧɧɨ ɫɥɟɞɭɸɬ ɢɡ ɨɩɪɟɞɟɥɟɧɢɹ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɨɠɢ-
ɞɚɧɢɹ. ɉɪɢ ɜɵɜɨɞɟ ɩɟɪɜɨɝɨ ɢɡ ɧɢɯ ɭɱɢɬɵɜɚɟɦ, ɱɬɨ ɩɨ ɫɚɦɨɦɭ
ɨɩɪɟɞɟɥɟɧɢɸ ɮɭɧɤɰɢɢ ɩɥɨɬɧɨɫɬɢ ɪɚɫɩɪɟɞɟɥɟɧɢɹ,
pxdx()
f
f
³
1 .
ɂɡ ɷɬɢɯ ɞɜɭɯ ɫɜɨɣɫɬɜ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɨɠɢɞɚɧɢɹ ɥɟɝɤɨ ɩɨ-
ɥɭɱɚɟɦ ɭɤɚɡɚɧɧɵɟ ɞɜɚ ɫɜɨɣɫɬɜɚ ɞɢɫɩɟɪɫɢɢ. Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ,
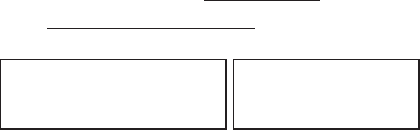
DX a E X a EX a
EX a EX a EX EX DX
()
(())(())()
2
22
,
D aX E aX E aX E aX aE X
Ea X EX aEX EX aDX
()
() ()
22
2
2
2
2
2
.
21
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɢɡɦɟɧɟɧɢɟ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɧɚ ɧɟɤɨ-
ɬɨɪɭɸ ɩɨɫɬɨɹɧɧɭɸ ɜɵɡɵɜɚɟɬ ɬɚɤɨɟ ɠɟ ɢɡɦɟɧɟɧɢɟ ɦɚɬɟɦɚɬɢɱɟ-
ɫɤɨɝɨ ɨɠɢɞɚɧɢɹ, ɧɨ ɧɟ ɨɬɪɚɠɚɟɬɫɹ ɧɚ ɞɢɫɩɟɪɫɢɢ. ɂɡɦɟɧɟɧɢɟ
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɜ
a ɪɚɡ ɩɪɢɜɨɞɢɬ ɤ ɬɚɤɨɦɭ ɠɟ ɢɡɦɟɧɟɧɢɸ
ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɨɠɢɞɚɧɢɹ ɢ ɢɡɦɟɧɹɟɬ ɡɧɚɱɟɧɢɟ ɞɢɫɩɟɪɫɢɢ ɜ
a
2
ɪɚɡ.
ȼ ɩɪɢɦɟɧɟɧɢɢ ɤ ɥɢɧɟɣɧɨɣ ɦɨɞɟɥɢ ɧɚɛɥɸɞɟɧɢɣ
yxin
iii
D
E
H
, 1, , ,
ɫ ɮɢɤɫɢɪɨɜɚɧɧɵɦɢ
xx
n1
,, ɢ ɜɡɚɢɦɧɨ ɧɟɡɚɜɢɫɢɦɵɦɢ ɝɚ-
ɭɫɫɨɜɫɤɢɦɢ ɨɲɢɛɤɚɦɢ
H
H
1
,,
n
, ɦɵ ɢɦɟɟɦ:
H
i
a
NYx
iii
0
2
,
VDEH
a
Nx
i
DE V
.,
2
ɋɨɨɬɜɟɬɫɬɜɟɧɧɨ,
ED EY xD
ii i ii
HHV DEHV
, 0
22
,() ; () () .
Ɂɚɦɟɬɢɦ, ɧɚɤɨɧɟɰ, ɱɬɨ ɟɫɥɢ
ZZ
n
1
,, — ɫɥɭɱɚɣɧɵɟ ɜɟɥɢ-
ɱɢɧɵ ɢ
ZZ Z
n
1
, ɬɨ
EZ EZ EZ
n
1
ɢ ɟɫɥɢ ɫɥɭɱɚɣɧɵɟ ɜɟɥɢɱɢɧɵ
ZZ
n
1
,,
ɩɨɩɚɪɧɨ ɧɟɤɨɪɪɟɥɢ-
ɪɨɜɚɧɵ
, ɬ. ɟ.
CovZZ EZEZZEZ
jk j j k k
,()() 0 ,
ɬɨ ɬɨɝɞɚ
DZ DZ DZ
n
1
.
ȼ ɩɪɢɦɟɧɟɧɢɢ ɤ ɩɨɫɥɟɞɧɟɣ ɥɢɧɟɣɧɨɣ ɦɨɞɟɥɢ ɧɚɛɥɸɞɟɧɢɣ
ɷɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɪɚɫɫɦɚɬɪɢɜɚɟɦɚɹ ɤɚɤ ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ
ɨɰɟɧɤɚ ɧɚɢɦɟɧɶɲɢɯ ɤɜɚɞɪɚɬɨɜ
E
, ɤɨɬɨɪɭɸ ɦɵ ɩɪɟɞɫɬɚɜɢɥɢ ɪɚ-
ɧɟɟ ɜ ɜɢɞɟ
E
¦
cY
i
i
n
i
1
,

22
ɝɞɟ
cww
ii
,
w
xx
xx
i
i
i
i
n
¦
2
1
,
ɬɚɤ ɱɬɨ
cc
n1
,,
— ɮɢɤɫɢɪɨɜɚɧɧɵɟ ɜɟɥɢɱɢɧɵ, ɢɦɟɟɬ ɧɨɪ-
ɦɚɥɶɧɨɟ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɫ ɦɚɬɟɦɚɬɢɱɟɫɤɢɦ ɨɠɢɞɚɧɢɟɦ
EcEY
i
i
n
i
(
)(
E
¦
1
)
ɢ ɞɢɫɩɟɪɫɢɟɣ
DcDY
i
i
n
i
(
)(
E
¦
2
1
) .
2.4. ɇɈɊɆȺɅɖɇɕȿ ɅɂɇȿɃɇɕȿ ɆɈȾȿɅɂ ɋ
ɇȿɋɄɈɅɖɄɂɆɂ ɈȻɔəɋɇəɘɓɂɆɂ ɉȿɊȿɆȿɇɇɕɆɂ
ɇɚɱɢɧɚɹ ɫ ɷɬɨɝɨ ɦɨɦɟɧɬɚ, ɦɵ ɛɭɞɟɦ ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ
(1) Ɇɨɞɟɥɶ ɧɚɛɥɸɞɟɧɢɣ
ɢɦɟɟɬ ɜɢɞ
yx x i nnp
ii pipi
t
T
T
H
,
11
1,,, ,
ɝɞɟ
y
i
- ɡɧɚɱɟɧɢɟ ɨɛɴɹɫɧɹɟɦɨɣ ɩɟɪɟɦɟɧɧɨɣ ɜ i -ɦɧɚ-
ɛɥɸɞɟɧɢɢ;
x
ij
- ɢɡɜɟɫɬɧɨɟ ɡɧɚɱɟɧɢɟ j -ɨɣ ɨɛɴɹɫɧɹɸɳɟɣ ɩɟɪɟɦɟɧ-
ɧɨɣ ɜ i -ɦ ɧɚɛɥɸɞɟɧɢɢ;
T
j
- ɧɟɢɡɜɟɫɬɧɵɣ ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɢ j -ɨɣ ɨɛɴɹɫɧɹɸ-
ɳɟɣ ɩɟɪɟɦɟɧɧɨɣ;
H
j
- ɫɥɭɱɚɣɧɚɹ ɫɨɫɬɚɜɥɹɸɳɚɹ (“ɨɲɢɛɤɚ“) ɜ i -ɦɧɚ-
ɛɥɸɞɟɧɢɢ.
(2)
H
H
1
,,
n
- ɫɥɭɱɚɣɧɵɟ ɜɟɥɢɱɢɧɵ
,
ɧɟɡɚɜɢɫɢɦɵɟ ɜ ɫɨ-
ɜɨɤɭɩɧɨɫɬɢ
, ɢɦɟɸɳɢɟ
ɨɞɢɧɚɤɨɜɨɟ ɧɨɪɦɚɥɶɧɨɟ ɪɚɫɩɪɟɞɟɥɟ-

23
ɧɢɟ N (0,
V
2
)
ɫ ɧɭɥɟɜɵɦ ɦɚɬɟɦɚɬɢɱɟɫɤɢɦ ɨɠɢɞɚɧɢɟɦ ɢ ɞɢɫɩɟɪ-
ɫɢɟɣ
V
2
0! .
(3)
ȿɫɥɢ ɧɟ ɨɝɨɜɨɪɟɧɨ ɩɪɨɬɢɜɧɨɟ, ɬɨ ɜ ɱɢɫɥɨ ɨɛɴɹɫɧɹɸ-
ɳɢɯ ɩɟɪɟɦɟɧɧɵɯ
ɜɤɥɸɱɚɟɬɫɹ ɩɟɪɟɦɟɧɧɚɹ, ɬɨɠɞɟɫɬɜɟɧɧɨ
ɪɚɜɧɚɹ ɟɞɢɧɢɰɟ
, ɤɨɬɨɪɚɹ ɨɛɴɹɜɥɹɟɬɫɹ
ɩɟɪɜɨɣ
ɨɛɴɹɫɧɹɸɳɟɣ
ɩɟɪɟɦɟɧɧɨɣ, ɬɚɤ ɱɬɨ
xi n
i
1
11{ ,,,.
ɉɪɢ ɫɞɟɥɚɧɧɵɯ ɩɪɟɞɩɨɥɨɠɟɧɢɹɯ
yy
n1
,, ɹɜɥɹɸɬɫɹ ɧɚ-
ɛɥɸɞɚɟɦɵɦɢ ɡɧɚɱɟɧɢɹɦɢ ɧɨɪɦɚɥɶɧɨ ɪɚɫɩɪɟɞɟɥɟɧɧɵɯ ɫɥɭɱɚɣ-
ɧɵɯ ɜɟɥɢɱɢɧ YY
n
1
,,
,
ɤɨɬɨɪɵɟ ɧɟɡɚɜɢɫɢɦɵ ɜ ɫɨɜɨɤɭɩɧɨɫɬɢ ɢ
ɞɥɹ ɤɨɬɨɪɵɯ
EY x x DY
ii pip i
() () ,
TT V
,
11
2
ɬɚɤ ɱɬɨ
Y
i
a Nx x i n
ipip
(),,,.
TTV
,
11
2
1
ȼ ɨɬɥɢɱɢɟ ɨɬ
H
H
1
,,
n
,
ɫɥɭɱɚɣɧɵɟ ɜɟɥɢɱɢɧɵ YY
n
1
,,
ɢɦɟɸɬ ɪɚɫɩɪɟɞɟɥɟɧɢɹ, ɨɬɥɢɱɚɸɳɢɟɫɹ ɫɞɜɢɝɚɦɢ
.
Ɉɩɪɟɞɟɥɟɧɧɭɸ ɭɤɚɡɚɧɧɵɦ ɨɛɪɚɡɨɦ ɦɨɞɟɥɶ ɧɚɛɥɸɞɟɧɢɣ ɦɵ
ɛɭɞɟɦ ɧɚɡɵɜɚɬɶ
ɧɨɪɦɚɥɶɧɨɣ ɥɢɧɟɣɧɨɣ ɦɨɞɟɥɶɸ
ɫ
p
ɨɛɴɹɫ-
ɧɹɸɳɢɦɢ ɩɟɪɟɦɟɧɧɵɦɢ. ɂɧɚɱɟ ɟɟ ɟɳɟ ɧɚɡɵɜɚɸɬ
ɧɨɪɦɚɥɶɧɨɣ
ɥɢɧɟɣɧɨɣ ɦɨɞɟɥɶɸ ɦɧɨɠɟɫɬɜɟɧɧɨɣ ɪɟɝɪɟɫɫɢɢ ɩɟɪɟɦɟɧɧɨɣ y
ɧɚ ɩɟɪɟɦɟɧɧɵɟ x
1
, ... , x
p
. Ɍɟɪɦɢɧ “ɦɧɨɠɟɫɬɜɟɧɧɚɹ” ɭɤɚɡɵɜɚɟɬ
ɧɚ ɢɫɩɨɥɶɡɨɜɚɧɢɟ ɜ ɩɪɚɜɨɣ ɱɚɫɬɢ ɦɨɞɟɥɢ ɧɚɛɥɸɞɟɧɢɣ ɞɜɭɯ ɢ
ɛɨɥɟɟ ɨɛɴɹɫɧɹɸɳɢɯ ɩɟɪɟɦɟɧɧɵɯ, ɨɬɥɢɱɧɵɯ ɨɬ ɩɨɫɬɨɹɧɧɨɣ.
Ɍɟɪɦɢɧ “ɪɟɝɪɟɫɫɢɹ” ɢɦɟɟɬ ɨɩɪɟɞɟɥɟɧɧɵɟ ɢɫɬɨɪɢɱɟɫɤɢɟ ɤɨɪɧɢ
ɢ ɢɫɩɨɥɶɡɭɟɬɫɹ ɥɢɲɶ ɜ ɫɢɥɭ ɬɪɚɞɢɰɢɢ.
Ɉɰɟɧɢɜɚɧɢɟ
ɧɟɢɡɜɟɫɬɧɵɯ ɤɨɷɮɮɢɰɢɟɧɬɨɜ ɦɨɞɟɥɢ
ɦɟɬɨ-
ɞɨɦ ɧɚɢɦɟɧɶɲɢɯ ɤɜɚɞɪɚɬɨɜ
ɫɨɫɬɨɢɬ ɜ ɦɢɧɢɦɢɡɚɰɢɢ ɩɨ ɜɫɟɦ
ɜɨɡɦɨɠɧɵɦ ɡɧɚɱɟɧɢɹɦ
T
T
1
,,
p
ɫɭɦɦɵ ɤɜɚɞɪɚɬɨɜ

24
Qyxx
piipip
i
n
TT T T
111
2
1
,.
¦
Ɇɢɧɢɦɭɦ ɷɬɨɣ ɫɭɦɦɵ ɞɨɫɬɢɝɚɟɬɫɹ ɩɪɢ ɧɟɤɨɬɨɪɨɦ ɧɚɛɨɪɟ
ɡɧɚɱɟɧɢɣ ɤɨɷɮɮɢɰɢɟɧɬɨɜ
TT TT
1
,,
,
1
pp
ɬɚɤ ɱɬɨ
QQ
pp
p
,
min , .
,,
TT TT
TT
11
1
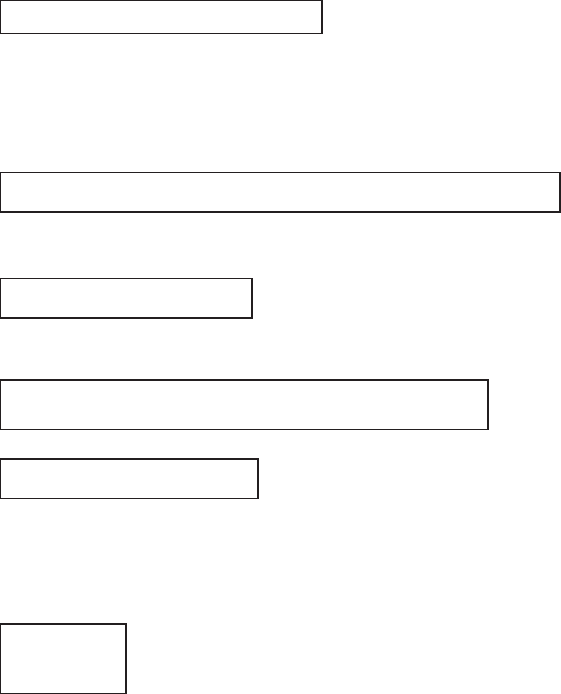
ɗɬɨ ɦɢɧɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɦɵ ɨɩɹɬɶ ɨɛɨɡɧɚɱɚɟɦ RSS ,
ɬɚɤ ɱɬɨ
RSS y x x
ii pip
i
n
¦
,
TT
11
2
1
ɢ ɧɚɡɵɜɚɟɦ
ɨɫɬɚɬɨɱɧɨɣ ɫɭɦɦɨɣ ɤɜɚɞɪɚɬɨɜ
.
Ʉɨɷɮɮɢɰɢɟɧɬ ɞɟɬɟɪɦɢɧɚɰɢɢ R
2
ɨɩɪɟɞɟɥɹɟɬɫɹ ɤɚɤ
R
RSS
TSS
2
1
ɝɞɟ
TSS y y
i
i
n
¦
2
1
.
Ɉɛɨɡɧɚɱɚɹ
,,,yx xi n
ii pip
TT
,
11
1
(
ɩɨɞɨɛɪɚɧɧɵɟ - fitted
- ɡɧɚɱɟɧɢɹ ɨɛɴɹɫɧɹɸɳɟɣ ɩɟɪɟɦɟɧɧɨɣ
ɩɨ ɨɰɟɧɟɧɧɨɣ ɥɢɧɟɣɧɨɣ ɦɨɞɟɥɢ ɫɜɹɡɢ), ɢ ɨɩɪɟɞɟɥɹɹ
ɨɫɬɚɬɨɤ
(
residual
)
ɨɬ i-ɝɨ ɧɚɛɥɸɞɟɧɢɹ
ɤɚɤ
eyy
iii
,
ɦɵ ɩɨɥɭɱɚɟɦ:
