Nof S.Y. Springer Handbook of Automation

Подождите немного. Документ загружается.

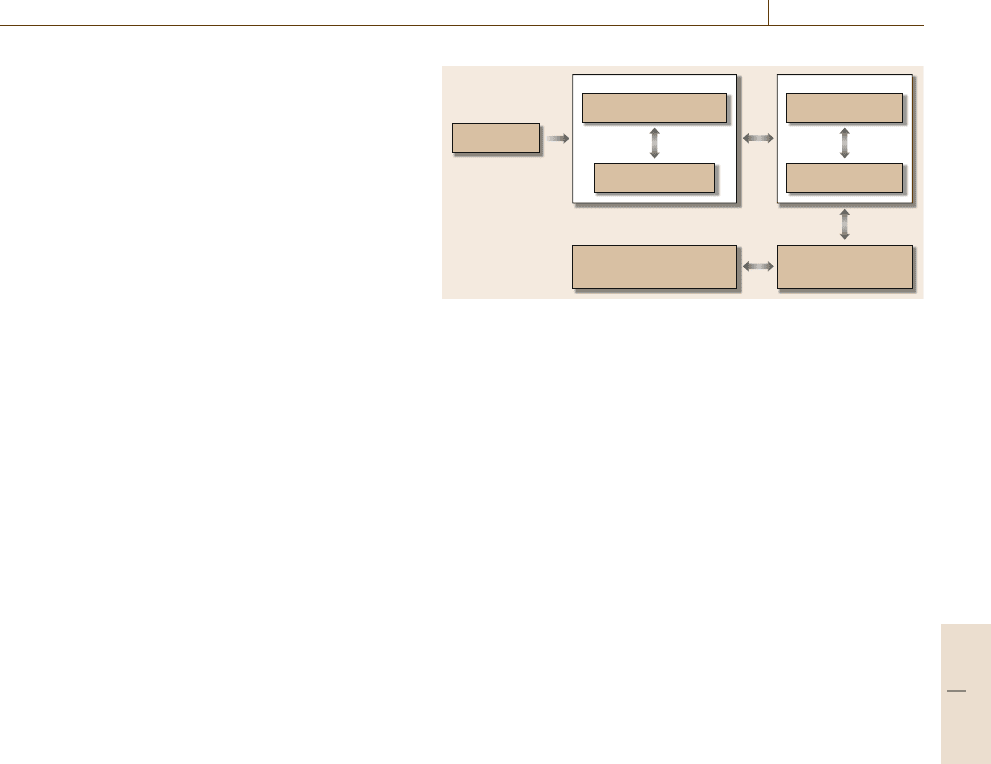
Machining Lines Automation 35.3 Line Balancing 605

should be performed for the optimal reconﬁguration

of the transfer line (note that this is rarely consid-

ered for dedicated lines of mass production; more

precisely, a reconﬁguration of a dedicated line deals

with speciﬁc engineering approaches). As illustrated

in Fig. 35.6, these steps are executed sequentially. Of

course, the designer can return to the previous steps as

often as necessary (i. e., the decision-making process is

iterative).

Such a methodology was already implemented in

a decision-aid software tool for the preliminary de-

sign of dedicated transfer lines [35.12]. The developed

software includes a database of parameterized features

for product analysis. The product analysis provides

a set of features which will be used at the process

planning step. The process planning generates sev-

eral process plans with the best one chosen for each

feature. A set of operations and constraints are ob-

tained. Then, a type of transfer line is selected by

considering the process plans, part dimensions, re-

quired productiveness, cost of equipment, variability

and longevity of market demand, etc. For the obtained

process plans and production system type, the corre-

sponding line balancing problem is solved. Finally, an

estimation of the cost of the production system is made.

If the solution or the cost is unsatisfactory, the de-

signer can modify the data and constraints and restart

the procedure.

Definition of operations

Process planning

Detailed design and

implementation of the line

Evaluation and

simulation

Choice of line type

Balancing the line

New product

Fig. 35.6 Design of transfer lines

While this software was initially developed to de-

sign dedicated transfer lines, the general methodology

is valid for all transfer lines (dedicated, ﬂexible or re-

conﬁgurable). The difference is that for the dedicated

transfer line it is applied once (at the preliminary de-

sign stage). In the case of ﬂexible transfer lines, thistool

should be used in real time, each time a new product is

launched. For reconﬁgurable transfer lines, it is useful

for each physical reconﬁguration of the line.

This approach is based on a set of engineering

procedures, knowledge-based constraints, and some op-

timization techniques for transfer line balancing. The

optimization techniques are the core (and originality) of

this methodology, which is why, the rest of this chapter

will consider this aspect.

35.3 Line Balancing

As aforementioned, the line balancing (assignment of

operation to workstations) is the key problem in the

design of transfer lines.

Historically, the line balancing problem was ﬁrst

stated for assembly lines. As far as we know, the earli-

est publication on assembly line balancing (ALBP) was

presented by Salveson [35.13]. Furthermore, exhaustive

studies were made by several researchers in the last

50years, with many interesting applications covered.

One comprehensive state of the art has been presented

in a special issue [35.14]. Several articles provide broad

surveys of this problem; see, for example [35.15–20].

To summarize, the ALBP is NP-hard; see, for exam-

ple [35.21]. Much research has been generated to solve

the problem by developing approximate or exact meth-

ods [35.22–32].

The problem of machining line balancing is rather

recent. This problem was mentioned in [35.33]. In Dol-

gui et al. [35.34], it was deﬁned for dedicated transfer

lines and ﬁrst called transfer line balancing problem

(TLBP).

Industry favors solving TLBP because the machin-

ing lines become too expensive otherwise. The TLBP

consists of answering the following questions:

1. Which machining units are to be chosen to execute

the required operations?

2. How many workstations are necessary?

3. How should the machining units be assigned to the

stations?

These questions can be answered by an intelligent

assignment of operations and machining units to work-

stations, minimizing the line cost while satisfying the

objective production rate as well as respecting all other

constraints.

Part D 35.3

606 Part D Automation Design: Theory and Methods for Integration

Several exact and approximate (or heuristic) meth-

ods for TLBP have been proposed. Exact methods are

useful to better understand the problem, however for

large-scale problems they require excessive computa-

tion time. Contrarily, approximate methods can provide

quicker results but do not guarantee the optimality of

solutions. Additionally, a heuristic algorithm is often

easier to develop than optimal procedures.

The most signiﬁcantmethods foran exact resolution

of the TLBP are:

•

Linear programming in mixed variables: the prob-

lem is modeled as a mixed integer program and

solved with an optimization tool such as ILOG

Cplex [35.35–37].

•

Dynamic programming: a recursive method used

for the resolution of problems having an additive

objective function. Examples of this approach for

TLBP are given in [35.33, 34, 38, 39], where the

initial problems were transformed into constrained

shortest-path problems and solved with appropriate

algorithms.

•

Branch and bound: an implicit enumerative proce-

dure which avoids verifying all solutions. Several

works use this approach for the resolution of the

TLBP; see, for example, [35.40,41].

Also, the column generation method can be used for

TLBP. Indeed, it was already successfully used for as-

sembly line balancing; see, for example, [35.42].

For large-scale problems, or when the allocated

computing time is severely limited (e.g., for ﬂexi-

ble transfer lines), several approximate methods have

been designed. We classify these methods into two

categories:

1. Heuristics based on priority rules derived from the

methods for ALBP. There are several heuristic algo-

rithms, which differ in the rule(s) used:

– Ranked positioned weight (RPW) [35.22]):

based on the weights of the operations cal-

culated from their execution time and the

operational times of their successors [35.43].

– Computer method of sequencing operations for

assembly lines (COMSOAL) [35.24]): solutions

are generated by assigning operations randomly

to the stations [35.44–47].

2. Metaheuristics, i.e., solving strategies applicable

to a wide range of combinatorial optimization

problems:

– A multistart decomposition approach was sug-

gested in [35.43,48].

An example of machining line balancing via simulation

can be found in [35.49].

Note that most of these methods were developed

for dedicated transfer lines. In the next section, we will

show how this approach can be applied to ﬂexible and

reconﬁgurable transfer lines. To illustrate, an industrial

case study will be presented with a mixed integer pro-

gramming model.

35.4 Industrial Case Study

35.4.1 Description of the Case Study

In Fig.35.7, the machining line considered in this case

study is presented. This line is designed to manufacture

automotive cylinder heads.It isequipped with CNC ma-

chines (machining centers) for the output of 1250 parts

per day. All the machines are identical (line modularity

principle), with some exceptions. In contrast to dedi-

cated transfer lines with multispindle machines, here,

each machine contains one spindle and a magazine for

tools. For each machine, to pass from one operation to

the next it is necessary to consider an additional time

due to tool changes and displacements or/and the ro-

tation of the part (setup time). Taking into account the

fact that a part is held at a machine with some ﬁxtures in

a given position (part ﬁxing and clamping), some faces

and elements of the part are not accessible for machin-

ing even after part displacement or rotation. Whatever

positioning and clamping are chosen some areas on the

part will be hidden or covered. Therefore, the choice of

a part position for part ﬁxing should be also considered

in the optimization procedure.

In Fig.35.7, lines (1) represent the transport sys-

tem composed of conveyors. Robots are used for part

loading and unloading. The boxes (2) represent the

CNC machines. Machines in a group aligned vertically

represent a workstation. Then a workstation can com-

prise more than one machine; in this case, the same

operations are duplicated and executed on different ma-

chines. With the parallel machines at each station, the

line is easily reconﬁgurable. The line cycle time can

be modiﬁed, if necessary, and even be shorter than the

Part D 35.4

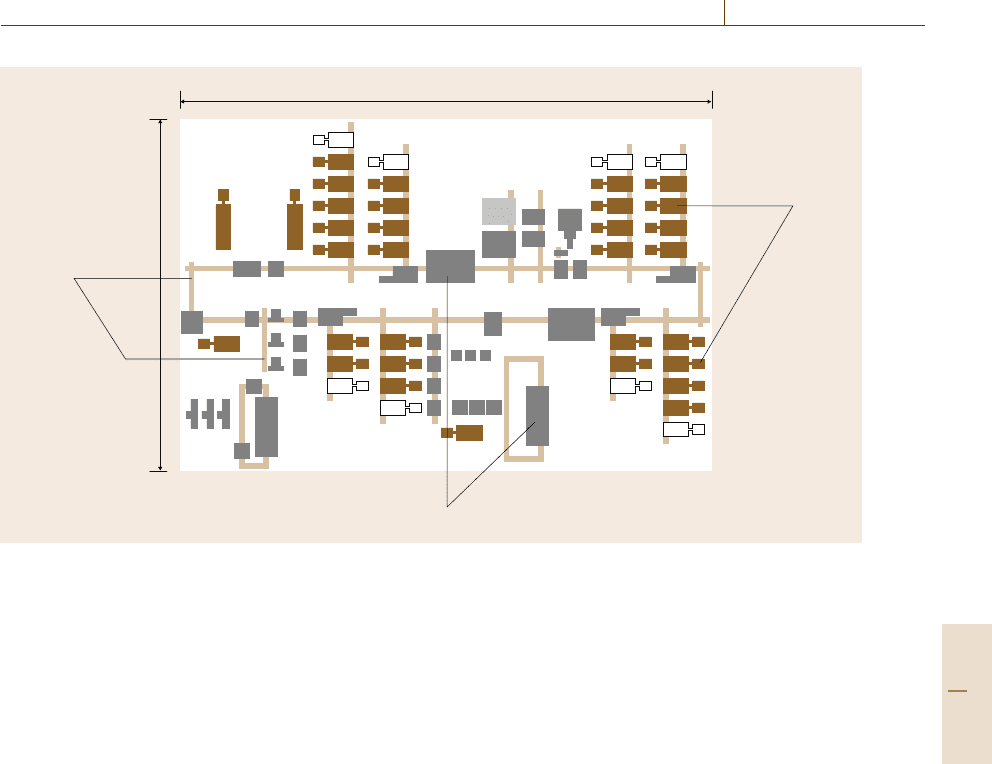
Machining Lines Automation 35.4 Industrial Case Study 607

(2)

(3)

(1)

80000

42000

• 1250 parts/day

• 32 machines

Fig. 35.7 Schema of a line for machining cylinder heads (PCI/SCEMM)

time of an operation. The boxes (3) represent dedi-

cated stations for speciﬁc operations such as assembly

or washing.

To help the designer of this line, we developed

a model for line balancing. The input data used were:

•

Cycle time (takt time) imposed by the objective pro-

duction rate: one part is produced at each cycle.

•

Precedence constraints: relations of order between

operations. These relations deﬁne feasible se-

quences of operations.

•

Inclusion constraints: the need to carry out ﬁxed

groups of operations on the same workstation.

•

Exclusion constraints: the impossibility of carry-

ing out certain subsets of operations at the same

workstation.

•

Accessibility constraints: these are related to the

positioning of the part; indeed, for a position

some part sides are not accessible, and thus opera-

tions on these sides cannot be carried out without

repositioning. In the considered machining line,

only one part ﬁxing position is deﬁned for each

workstation (part repositioning occurs between two

stations).

•

Sequence-dependent setup times: the time required

for the execution of two sequential operations is not

equal to the sum of their times but also depends on

the order in which they are done, because the time

needed for the displacement/change of tool and part

rotation are not negligible.

•

Parallel machines: at each workstation several iden-

tical CNC machines are installed. Thus, the local

cycle time of the workstation is equal to the num-

ber of parallel machines multiplied by the line cycle

time (takt time). The machines of the same work-

station execute the same operations (in parallel on

different product units).

Hence, here, we have a special case of line balancing

with a sequential execution of operations, setup times,

parallel machines, as well as accessibility, exclusion,

and inclusions constraints.

The line of the case study can be regarded as re-

conﬁgurable. Indeed, while designed for the production

of a single product, if there are changes on the prod-

uct characteristics, the reconﬁguration of this line is

possible and easy thanks to:

•

The use of standard and identical CNC machining

centers, which simpliﬁes the reallocation of opera-

tions to the workstations.

•

At each station, machining centers can be added or

eliminated as needed thanks to this modularity.

Part D 35.4

608 Part D Automation Design: Theory and Methods for Integration

Now, we present a mixed integer programming

(MIP) model for the design of this line for a given prod-

uct. Furthermore, at the end of this section, we will give

an extension of this model which can be used when

reconﬁguring the line for another product.

35.4.2 Mixed Integer Programming (MIP)

To summarize the optimization problem, we will enu-

merate its main assumptions.

The set of all operations N to be executed at the line

is determined by the process plans for the product for

which the line is designed. A part to be machined will

pass through a sequence of workstations in the order of

their installation. Each workstation is provided with at

least one machine which carries out operations during

the line cycle time. In the case where workload time of

a workstation exceeds the line cycle time, parallel and

identical machines are installed. In this case, the local

cycle time is equal to the number of parallel machines

multiplied by the line cycle time. All machines of the

same station execute the same operations.

There are four types of additional constraints on

the assignment of the operations (as detailed earlier),

namely:

•

Precedence constraints

•

Exclusion constraints

•

Inclusion constraints

•

Accessibility constraints.

The time required for the execution of two operations is

not equal to the sum of their times but depends on the

sequence in which they are executed (Fig.35.8).

The optimization problem consists of assigning op-

erations to workstations to minimize the total number

of machines on the line while respecting the given

constraints.

Mathematical Model

We will introduce the following notations.

+ t

≠ t

+ t

ilj

lij

Fig. 35.8 Sequence-dependent setup times

Indexes:

•

i, j for operations

•

q for the place (order) of an operation in the se-

quence of assigned operations

•

n for the number of parallel machines at a worksta-

tion

•

k for the workstations

•

a for the part ﬁxing positions

Parameters:

•

N, the set of operations to be assigned (i, j =

1,...,|N|)

•

A, the set of possible part positions for part ﬁxing

in a machining center; only one of these positions is

chosen for each workstation; a part ﬁxing position

deﬁnes the accessibility constraints for the part (a =

1,...,|A|)

•

, the maximum number of operations authorized

to be assigned to a workstation: each workstation

created cannot contain more than l

operations

•

, the maximum number of machines on a work-

station

•

, the maximum number of workstations

•

·m

, the maximum number of possible as-

signments (places) for operations

•

, the operational time for operation i (i =

1,...,|N|)

•

, the setup time when operation j is processed

directly after operation i at the same workstation

•

, the objective line cycle time (takt time)

•

, the set of direct predecessors of operation i

•

∗

, the set of all predecessors of i (direct and indi-

rect predecessors)

•

∗

, the set of all successors of i (direct and indirect

successors)

•

ES, the collection of subsets e (e ⊂ N) of operations

which must be imperatively assigned to the same

workstation

•

ES, the set of pairs of operations (i, j) which cannot

be assigned to the same workstation

•

A(i), the set of the possible part ﬁxing positions for

which the execution of operation i is possible

•

S(k), the set of possible places for operations

at workstation k; this set is given by an in-

terval of indexes; the maximum possible inter-

val is S(k) ={l

(k−1)+1, l

(k−1)+2,...,l

k};

∀k =1, 2,...,m

•

K(i), the set of workstations on which operation i

can be processed: K(i) ⊆{1, 2,...,m

}

Part D 35.4

Machining Lines Automation 35.4 Industrial Case Study 609

•

Q(i), the set of possible places for operation i in the

sequence of all operations: Q(i) ⊆{1, 2,...,l

}

•

N(k), the set of operations which can be processed

at workstation k

•

M(q), the set of operations which can be assigned

to the place q in the sequence

•

, the earliest workstation to which operation i can

be assigned

•

, the last workstation to which operation i can be

assigned

Variables:

•

=1, if operation i is in qth place (q is its order in

the overall assignment sequence), otherwise x

•

, the setup time required between operations as-

signed to the same workstation in place q and q+1

(Fig.35.9);

•

=1, if there are n parallel machines at the work-

station k, 0 otherwise;

•

=1, if for the part of the workstation k the ﬁxing

position a is used, 0 otherwise.

Note that, if an operation is assigned to place q,itis

the q −(

q/l

−1)·l

th operation of the workstation

q/l

The optimization model is as follows:

•

The objective function (35.1) minimizes the total

number of machines

Minimize



k=1



n=1

n ·y

. (35.1)

•

Equation (35.2) veriﬁes that there is only one

value for the number of parallel machines on each

workstation



n=1

≤1, ∀k = 1, 2,...,m

. (35.2)

q–1

= t

Position q

Workstation k

Position q–1 Position q+1

Fig. 35.9 Deﬁnition of the parameter τ

•

Equation (35.3) assures that a workstation is open

only if the preceding workstation is also open



n=1

≥



n=1

n(k+1)

, ∀k = 1, 2,...,m

−1 .

(35.3)

•

Equation (35.4) assures that each operation i is as-

signed once and only once



q∈Q(i)

=1 , ∀i ∈ N . (35.4)

•

The constraints (35.5) assure that a place in the se-

quence is occupied by only one operation



i∈M(q)

≤1 , ∀q = 1, 2,...,q

. (35.5)

•

Equation (35.6) assures that an operationis assigned

to a place only ifanother operation is assigned to the

preceding place of the sequence (there is no empty

place in the sequence of assigned operations)



i∈M(q−1)

i(q−1)

≥



i∈M(q)

∀q ∈ S(k)\min{S(k)} , ∀k = 1, 2,...,m

(35.6)

•

Equation (35.7) veriﬁes that only one part ﬁxing

position is chosen for each workstation



a∈A

≤1 , ∀k = 1, 2,...,m

. (35.7)

•

Equation (35.8) assuresthat accessibilityconstraints

are respected (the part ﬁxing position chosen for

a workstation authorizes the execution of every op-

eration assigned to this station)



q∈S(k)

≤



a∈A(i)

, ∀k =1, 2,...,m

, ∀i ∈ N .

(35.8)

•

Equation (35.9) calculates the additional time be-

tween operation i and operation j when operation

j is processed directly after operation i at the same

workstation

≥t

·(x

j(q+1)

−1) ,

∀i ∈ M(q) , ∀j ∈ M(q +1) ,

∀q ∈ S(k)\max



S(k)



∀k = 1, 2, ..., m

. (35.9)

Part D 35.4

610 Part D Automation Design: Theory and Methods for Integration

•

Equation (35.10) assures that the workload time of

every workstation does not exceed the local cycle

time, which corresponds to the number of installed

parallel machines at this workstation multiplied by

the objective cycle time of the line



q∈S(k)\max{S(k)}



i∈N(k)



q∈S(k)

·x

≤ T



n=1

n ·y

, ∀k = 1, 2,...,m

(35.10)

•

Equation (35.11) deﬁnes the precedence constraints

between operations



q∈Q(j)

q ·x

≤



q∈Q(i)

q ·x

, ∀i ∈ N , ∀j ∈ P

(35.11)

•

Equation (35.12) representsthe inclusionconstraints



q∈S(k)∩Q(i)



q∈S(k)∩Q( j)

∀i, j ∈ e , ∀e ∈ES , ∀k ∈ K(i) .

(35.12)

•

Equation (35.13) representsthe exclusion constraints



q∈S(k)

) ≤1 ,

∀(i, j) ∈

ES , ∀k ∈ K(i)∩K( j) . (35.13)

•

Equations (35.14)–(35.17) provide additional con-

straints on the possible values of variables

≥0 , ∀q =1, 2,...,q

, (35.14)

∈{0, 1}, ∀i ∈ N , ∀q ∈ Q(i) , (35.15)

∈{0, 1},

∀n = 1, 2,...,n

, ∀k = 1, 2,...,m

, (35.16)

∈{0, 1}, ∀k = 1, 2,...,m

, ∀a ∈ A .

(35.17)

35.4.3 Computing Ranges for Variables

The model (35.1–35.17) can be solved using a stan-

dard operational research solver, for example, ILOG

Cplex. Nevertheless, the calculation time is prohibitive.

The resolution time for the model (35.1–35.17) can be

greatly decreased using efﬁcient techniques to reduce

the number of variables (the size of the model) and

consequently to accelerate the search for an optimal

solution.

We propose a technique for calculating bounds for

the possible indexes for the variables of the mathemat-

ical model. This can simplify the problem and thus

reduce the calculation time.

Taking into account the different constraints be-

tween operations, we can calculate the sets K(i), N(k),

S(k), Q(i), and M(q) more precisely. Note that these

sets give intervals of possible values for the correspond-

ing indexes.

The following additional notations can be deﬁned:

•

[r] is a recursive variable for the step by step cal-

culation of the value of E

taking into account setup

times between operations, r =0, 1.

•

[r] is a recursive variable for the step by step cal-

culation of the value of L

taking into account setup

times between operations, r =0, 1.

With P

∗

, which is the set of all predecessors of oper-

ation i,andF

∗

, which is the set of all successors of

operation i, we can also introduce:

•

[r]: the sum of the





∗



−E

[r]+1



shortest

setup times between the operations of the set P

∗

∪

{i}composed of operation i and all its predecessors,

i ∈ N

•

[r]: the sum of the





∗



−m

[r]



shortest

setup times between the operations of the set F

∗

∪

{i} composed of operation i and all its successors,

i ∈ N

•

d[i, j]: a parameter (distance) which has the follow-

ing property: if (i, j)or(j, i) ∈

ES,thend[i, j]=1,

else d[i, j]=0.

The total operational time T

sum

without considering the

setup times between operations is calculated as follows

sum



i∈N

A lower bound on the number of workstations can be

calculated by supposing that each workstation contains

machines. Therefore, the local cycle time of each

workstation is equal to (T

·n

). The line becomes a se-

rial linecomposed of identical workstations witha cycle

time which is equal to (T

·n

). Then, a lower bound on

the number of workstations LB

can be calculated as

follows

sum

/(T

·n

)

Part D 35.4

Machining Lines Automation 35.4 Industrial Case Study 611

where the notation

indicates the lowest integer

value higher than or equal to x.

In the same way, a lower bound on the number of

machines in the line (LB

) can be determined by the

following expression

sum

Thus, the following procedure calculates the sets K(i),

Q(i), M(q), N(k), and S(k). Note that the operations are

numbered in order of precedence graph ranks (in topo-

logical order). Somelines are annotatedwith comments.

The symbol “//” is used to mark the beginning and the

end of these comments.

Algorithm

Step 1 // step-by-step calculation of E

and L

,taking

into account precedence constraints and setup times//

for all i ∈ N do

begin

// calculate the earliest workstation E

[0] on which

operation i can be processed taking into account the

precedence constraints; note that an operation cannot be

processed before its predecessors //

[0]←

(

j∈P

∗

)/(n

·T

)

;

// calculate the latest workstation L

[0] on which op-

eration i can be processed considering the precedence

constraints, note that an operation cannot be processed

after its successors //

[0]←m

−

(

j∈F

∗

)/(n

·T

)

+1;

// calculate E

[1], which are new values of E

ob-

tained by taking into account in addition setup times

between operations //

[1]←

+Sp

[0]+

(

j∈P

∗

)/(n

·T

)

;

// calculate L

[1], which are new values of L

ob-

tained by taking into account in addition setup times

between operations //

[1]←m

−

+Sf

[0]+

(

j∈F

∗

)/(n

·T

)

+1;

// updating the values of E

if E

[1]= E

[0] then E

←max



[0]+1,

+Sp

[1]+

(

j∈P

∗

))/(n

·T

)

5

else E

← E

[1];

// updating the values of L

if L

[1]= L

[0] then L

←min



[0]−1,

−



+Sf

[1]+

(

j∈F

∗



/(n

·T

)



else L

← L

[1];

end

Step 2 // step-by-step calculation of E

, taking into ac-

count exclusion and inclusion constraints//

cur

←1;

min

← j

cur

;

cur

←|N|;

// new values of E

are calculated by considering

exclusion constraints //

for j ← j

min

+1,...,|N| do

←max



max

i∈P

∗



+d[i, j]



, E



;

for each e ∈ES

begin

←max

j∈e

);

for each j ∈e if E

< E

then

begin

// new value of E

is calculated, now taking

into account an inclusion constraint//

← E

;

cur

←min{j

cur

, j};

end

until j

cur

=|N|.

Step 3 // step-by-step calculation of L

, taking into ac-

count inclusion and exclusion constraints //

cur

←|N|;

max

← j

cur

;

cur

←1;

// new values of L

are calculated by considering

exclusion constraints //

for j ← j

max

−1,...,1 do

←min



min

i∈F

∗



−d[j, i]



, L



;

for each e ∈ES

begin

←min

j∈e

);

for each j ∈e if L

> L

then

begin

// new values of L

are again calculated, now

taking into account inclusion constraints //

← L

;

cur

←max{j

cur

, j};

Part D 35.4

612 Part D Automation Design: Theory and Methods for Integration

, E

= 1 E

= 3E

, E

= 2

, L

= m

, L

= m

–1

Fig. 35.10 An example of initial values for E

and L

, E

= 1

= m

–2

, E

= 3E

, E

= 2

, L

= m

, L

= m

–1

mkj

liq

Fig. 35.11 Modiﬁed values of E

and L

taking into account setup

times

end

until j

cur

=1 .

Step 4 // calculation of the sets K(i), N(k), S(k), Q(i),

and M(q)//

for all i ∈ N do

K(i) ←[E

, L

];

for k ←1, 2,...,m

≥ E

+ 1

jjl

and

(i, j) ∈ ES

ili

jli

Fig. 35.12 An example of modiﬁcations of E

by considering an exclusion constraint

begin

N(k) ←{i|i ∈ N, k ∈ K(i)};

S(k) ←



k−1

(





S(k



)



, min





N(k)



, l



k−1

(





S(k



)





;

end

for all i ∈ N do

Q(i) ←



min



S(E

)



, max



S(L

)



;

for q ← 1, 2,...,max{S(m

)} do

M(q) ←{i|q ∈ Q(i)};

End of algorithm.

Some illustrations of the algorithm rules are pre-

sented in Figs. 35.10–35.13.

Numerical Example

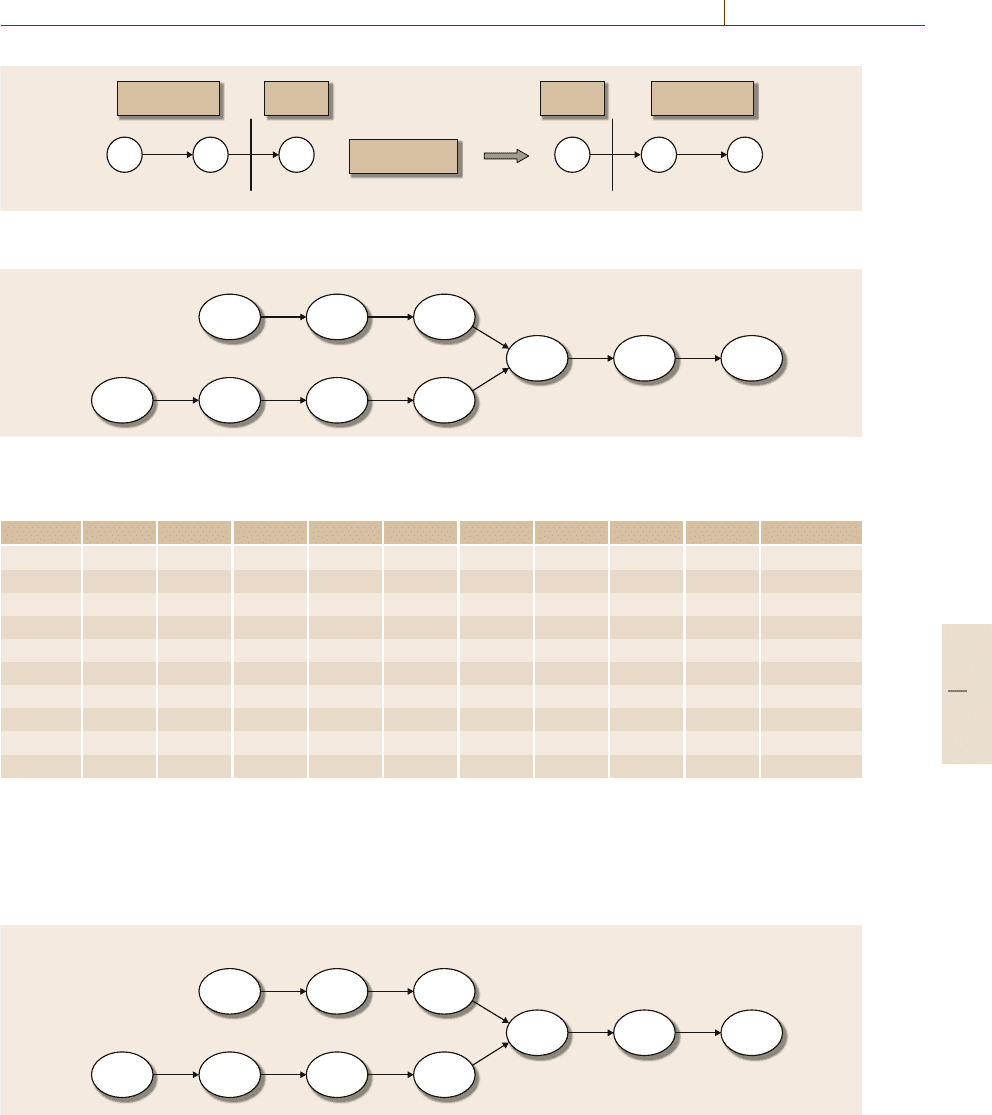
In order to better explain the suggested algorithm, we

present a numerical example with ten operations. Fig-

ure 35.14 shows the precedence graph and operational

times.

The objective line cycle time is: T

=16 units of

time; the maximum number of stations m

= 6; the

maximum number of machines to be installed on a sta-

tion n

=3; the maximum number of operations to be

assigned to a station l

=8.

The inclusion constraints are: ES ={(2, 4);(8, 9);

(5, 6)}.

The exclusion constraints are:

ES ={(2, 7);(3, 4)}.

The setup times are reported in Table 35.1.Forex-

ample, the setup time t

4,5

=3 corresponds to the time

that is required to perform operation 5immediately after

operation 4.

The totaloperational time, T

sum

(

i∈N

=161 units

of time.

Part D 35.4

Machining Lines Automation 35.4 Industrial Case Study 613

(l, j) ∈ ES

, E

= 1 E

= 2 E

= 1

, E

= 2

jli

Fig. 35.13 An example of modiﬁcation for E

by taking into account an inclusion constraint

2118

910

17161812

6543

Fig. 35.14 Precedence graph

Table 35.1 Setup times

ij1 2 3 4 5 6 7 8 9 10

1 – 4 4 3 2 1 1 2 1.5 1.5

2 5 – 1.5 1 1 2.5 3 3 3 3.5

3 1.5 3.5 – 2.5 1.2 3.4 4 4.2 3 2.2

4 4.5 4 3 – 3 1.5 3 2 4.5 1.8

5 4 4 5 5 – 2.5 2 2 4.5 1

6 25 1.5 3 1.2 1 – 2 2 3 4

7 4 3.8 3 1.8 4 3 – 4.7 4 1.4

8 3 2.5 4 3.4 3.2 2.4 1.6 – 2 4

9 3 4.9 4 2.3 1.6 3.6 3 1.2 – 3

10 1.5 4 1.5 4.6 3.7 2.2 2.7 1.2 4.8 –

A lower bound on the number of workstations is:

sum

/(T

·n

)

= 161/(16·3)"=4.

Thus, the optimal solution cannot have fewer than

four workstations.

= 3, L

= 5

= 1, L

= 5

= 1, L

= 5

= 4, L

= 6E

= 4, L

= 6

910

= 1, L

= 4

= 2, L

= 5E

= 2, L

= 5E

= 1, L

= 4E

= 1, L

= 4

6543

Fig. 35.15 Va lu es o f E

and L

obtained considering precedence constraints and setup times

A lower bound on the number of machines is:

sum

= 161/16"=11.

Then, the optimal solution cannot have fewer than

11 machines.

Part D 35.4

614 Part D Automation Design: Theory and Methods for Integration

= 4

= 3

= 2

= 4E

= 4

910

= 1

= 2E

= 1

6543

Fig. 35.16 Va lu es o f E

considering exclusion and inclusion constraints

= 5

= 4

= 6L

= 5

910

= 4

= 5L

= 4L

= 3

6543

Fig. 35.17 Va lu es o f L

considering exclusion and inclusion constraints

Now, the procedure of range calculation for indexes

is applied:

•

Step 1 The initial values of E

and L

for each opera-

tion are calculated considering set-up times between

operations and precedence constraints (Fig.35.15).

•

Step 2 The new values of E

are obtained by

considering the exclusion and inclusion constraints

(Fig.35.16).

•

Step 3 The new values of L

are calculated by

considering the exclusion and inclusion constraints

(Fig.35.17).

•

Step 4

–SetsK(i) for operations i ∈ N are obtained (Ta-

ble 35.2)

Table 35.2 The ranges K(i) for the operations

Operation i 1 2 3 4 5 6 7 8 9 10

K(i) [1,4] [2,4] [1,3] [2,4] [2,5] [2,5] [3,5] [4,5] [4,5] [4,6]

Table 35.3 The set of operations N(k) for each station

Station k 1 2 3 4 5 6

N(k) {1,3} {1,2,3,4,5,6} {1,2,3,4,5,6,7} {1,2,4,5,6,7,8,9,10} {5,6,7,8,9,10} {10}

Table 35.4 The ranges of places S(k) for stations

Station k 1 2 3 4 5 6

S(k) [1,2] [3,8] [9,15] [16,23] [24,29] [30,30]

– Sets of operations N(k) for stations k =

1, 2,...,m

are deﬁned (Table 35.3)

– Range of places S(k) for operations of station k

is calculated, k =1, 2,...,m

(Table 35.4)

– Finally, the range of places Q(i) for operation i

is found, for all i ∈ N (Table 35.5).

35.4.4 Reconﬁguration of the Line

As indicated at the beginning of this section, the stud-

ied line is reconﬁgurable. After the implementation of

the line, if there are changes in the product character-

istics or if there is a new product to be machined, the

line can be reconﬁgured. Such a reconﬁguration prob-

lem consists of reassigning operations to the stations

Part D 35.4