Nof S.Y. Springer Handbook of Automation

Подождите немного. Документ загружается.

Control Theory for Automation – Advanced Techniques 10.5 H

∞

Optimal Control 185

It isimportant to prove thatthe jointstate estimation and

control lead to stable closed-loop control. The proof is

based on observing that the complete system satisﬁes

the following state equations



x−





A−B

0A−L



x−





−L



w .

This form clearly shows that the poles introduced by the

controller and those introduced by the observer are sep-

arated from each other. The concept is therefore called

the separation principle. The importance of this obser-

vation lies in the fact that, in the course of the design

procedure the controller poles and the observer poles

can be assigned independently from each other. Note

that the control law u(t) =−K

x(t) still exhibits an op-

timal controller in the sense that F(G(iω), K(iω))

minimized.

10.5 H

∞

Optimal Control

Herewithbelow the optimal control in H

∞

sense will be

discussed. The H

∞

optimal control minimizes the H

∞

norm of the overall transfer function of the closed-loop

system

∞

=F(G(iω), K(iω))

∞

using a state variable feedback with a constant gain,

where F[G(s), K(s)] denotes the overall transfer func-

tion matrix of the closed-loop system [10.2,6,6,13]. To

minimize J

∞

requires rather involved procedures. As

one option, γ -iteration has already been discussed ear-

lier. In short, as earlier discussionson the norms pointed

out, the H

∞

norm can be calculated using L

norms by

∞

=sup



z

w

:w

=0



10.5.1 State-Feedback Problem

If all the state variables are available then the state vari-

able feedback

u(t) =−K

∞

x(t)

is used with the gain K

∞

minimizing J

∞

. Similarly to

the H

optimal control discussed earlier, in each step

of the γ -iteration K

∞

can be obtained via P

as the

symmetrical positive-deﬁnite or positive-semideﬁnite

solution of the



A−P







−1



+γ

−2



Riccati equation, provided that the matrix

A−B







−1



+γ

−2



represents a stable system (i.e., all the eigenvalues are

on the left-hand half plane). Once P

belonging to the

minimal γ value has been found the state variable feed-

back is realized by using the feedback gain matrix of

∞

=(D



)

−1



10.5.2 State-Estimation Problem

The optimal state estimation in H

∞

sense requires to

minimize

∞

=sup



z −

z

w

:w

=0



as a function of L. Again, minimization can be per-

formed by γ -iteration. Speciﬁcally, γ

min

is looked for to

satisfy J

∞

<γ with γ>0forallw. To ﬁnd the optimal

∞

gain the symmetrical positive-deﬁnite or positive-

semideﬁnite solution of the following Riccati equation

is required



+AP

−P









−1

+γ

−2



provided that

A−P









−1

+γ

−2



represents a stable system, i.e., it has all its eigenval-

ues on the left-hand half plane. Finding the solution P

belonging to the minimal γ value, the optimal feedback

gain matrix is obtained by

∞









−1

Then

x(t) =A

x(t)+B

u(t)+L

∞

[y(t)−C

x(t)]

Part B 10.5

186 Part B Automation Theory and Scientiﬁc Foundations

is in complete harmony with the ﬁltering procedure ob-

tained earlier for the state reconstruction in H

sense.

10.5.3 Output-Feedback Problem

If the state variables are not available for feedback then

a K(s) controller satisfying J

∞

<γ is looked for. This

controller, similarly to the procedure followed by the

optimal control design, can be determined in two

phases: ﬁrst the unavailable states are to be estimated,

then state feedback driven by the estimated states is to

be realized. As far as the state feedback is concerned,

similarly to the H

optimal control law, the H

∞

optimal

control is accomplished by

u(t) =−K

∞

x(t) .

However, the H

∞

optimal state estimation is more in-

volved than the H

optimal state estimation. Namely

the H

∞

optimal state estimation includes the worst-case

estimation of the exogenous w input, and the feedback

matrix L

∞

needs to be modiﬁed, too. The L

∗

∞

modiﬁed

feedback matrix takes the following form

∗

∞



I−γ

−2



−1

∞



I−γ

−2



−1



)

−1

then the state estimation applies the above gain accord-

ing to

x(t) =(A+B

−2



)

x(t)+B

u(t)

∗

∞

[y(t)−C

x(t)].

Reformulating the above results into a transfer function

form gives

K(s) =K

∞



sI−A−B

−2



∞

∗

∞



−1

∗

∞

The above K(s) controller satisﬁes the norm inequal-

ity F(G(iω), K(iω))

∞

<γ and it results in a stable

control strategy if the following three conditions are

satisﬁed [10.6]:

•

is asymmetrical positive-semideﬁnitesolution of

the algebraic Riccati equation



A−P







−1



+γ

−2



=0 ,

provided that

A−B



)

−1



+γ

−2



is stable.

•

is a symmetrical positive-semideﬁnitesolution of

the algebraic Riccati equation



+AP

−P









−1

+γ

−2



=0 ,

provided that

A−P









−1

+γ

−2



is stable.

•

The largest eigenvalue of P

is smaller than γ

ρ(P

) <γ

The H

∞

optimal output feedback control design pro-

cedure minimizes the F(G(iω), K(iω))

∞

norm via

γ -iteration andwhile γ

min

is looked forall the three con-

ditions above should be satisﬁed. The optimal control in

∞

sense is accomplished by K(s) belonging to γ

min

Remark: Now that we are ready to design optimal

controllers in H

or H

∞

sense, respectively, it is worth

devoting a minute to analyze what can be expected from

these procedures. To compare the nature of the H

ver-

sus H

∞

norms a relation for G

should be found,

where the G

norm is expressed by the singular val-

ues. It can be shown that

G



2π

∞



−∞



(G(iω))dω



1/2

Comparing now the above expression with

G

∞

=sup

σ(G(iω))

it is seen that G

∞

represents the largest possible sin-

gular value, while G

represents the sum of all the

singular values over all frequencies [10.6].

10.6 Robust Stability and Performance

When designing control systems, the design proce-

dure needs a model of the process to be controlled.

So far it has been assumed that the design procedure

is based on a perfect model of the process. Stabil-

ity analysis based on the nominal process model can

be qualiﬁed as nominal stability (NS) analysis. Sim-

Part B 10.6

Control Theory for Automation – Advanced Techniques 10.6 Robust Stability and Performance 187

ilarly, closed-loop performance analysis based on the

nominal process model can be qualiﬁed as nominal

performance (NP) analysis. It is evident, however, that

some uncertainty is always present in the model. More-

over, an important purpose of using feedback is even

to reduce the effects of uncertainty involved in the

model. The classical approach introduced the notions

of the phase margin and gain margin as measures to

handle uncertainty. However, these measures are rather

crude and contradictory [10.13,22]. Though they work

ﬁne in a number of practical applications, they are not

capable of supporting the design for processes exhibit-

ing unusual frequency behavior (e.g., slightly damped

poles). The postmodern era of control theory places

special emphasis on modeling of uncertainties. Specif-

ically, wide classes of structured, as well as additively

or multiplicatively unstructured uncertainties have been

introduced and taken into account in the design proce-

dure. Modeling, analysis, and synthesis methods have

been developed under the name robust control [10.17,

23,24]. Note that the linear quadratic regulator (LQR)

design method inherits some measures of robustness,

however, in general the pure structure of the LQR regu-

lators does not guarantee stability margins [10.1,6].

As far as the unstructured uncertainties are con-

cerned, let G

(s) denote the nominal transfer function

matrix of the process. Then the true plant behavior can

be expressed by

G(s) =G

(s)+

(s) ,

G(s) =G

(s)[I+

(s)],

G(s) =[I+

(s)]G

(s) ,

where 

(s) represents an additive perturbation, 

(s)

an input multiplicative perturbation, and 

(s) an out-

put multiplicative perturbation. These perturbations are

assumed to be frequency independent with bounded



•

(s)

∞

norms concerning their size. Frequency de-

pendence can easily be added to the perturbations by

using appropriate pre- and post-ﬁlters.

All the above three perturbation models can be

transformed to a common form

G(s) =G

(s)+W

(s)(s)W

(s) ,

where (s)

∞

≤ 1. Uncertainties extend the gen-

eral control system conﬁguration outlined earlier

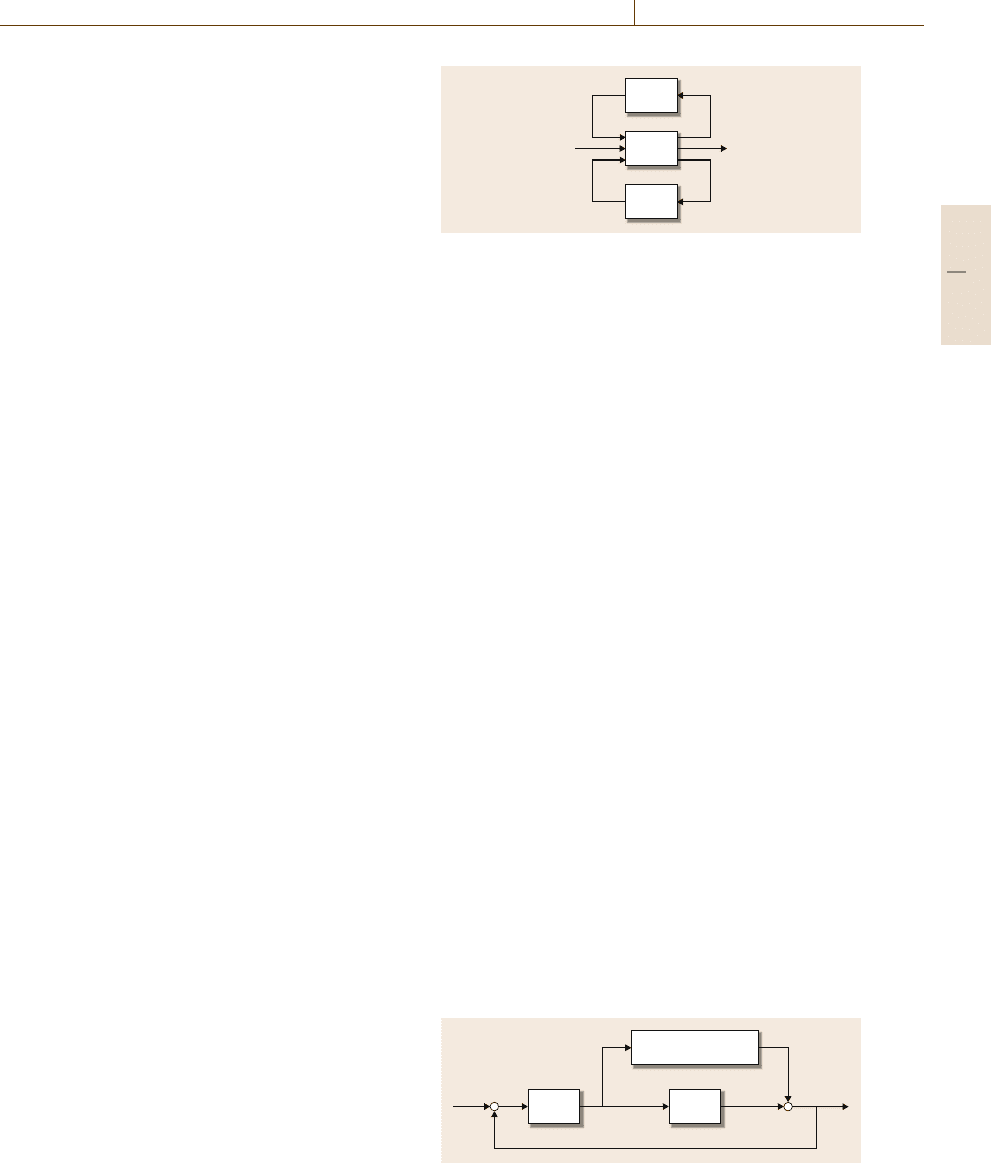
in Fig.10.6. The nominal plant now is extended by

a block representing the uncertainties and the feedback

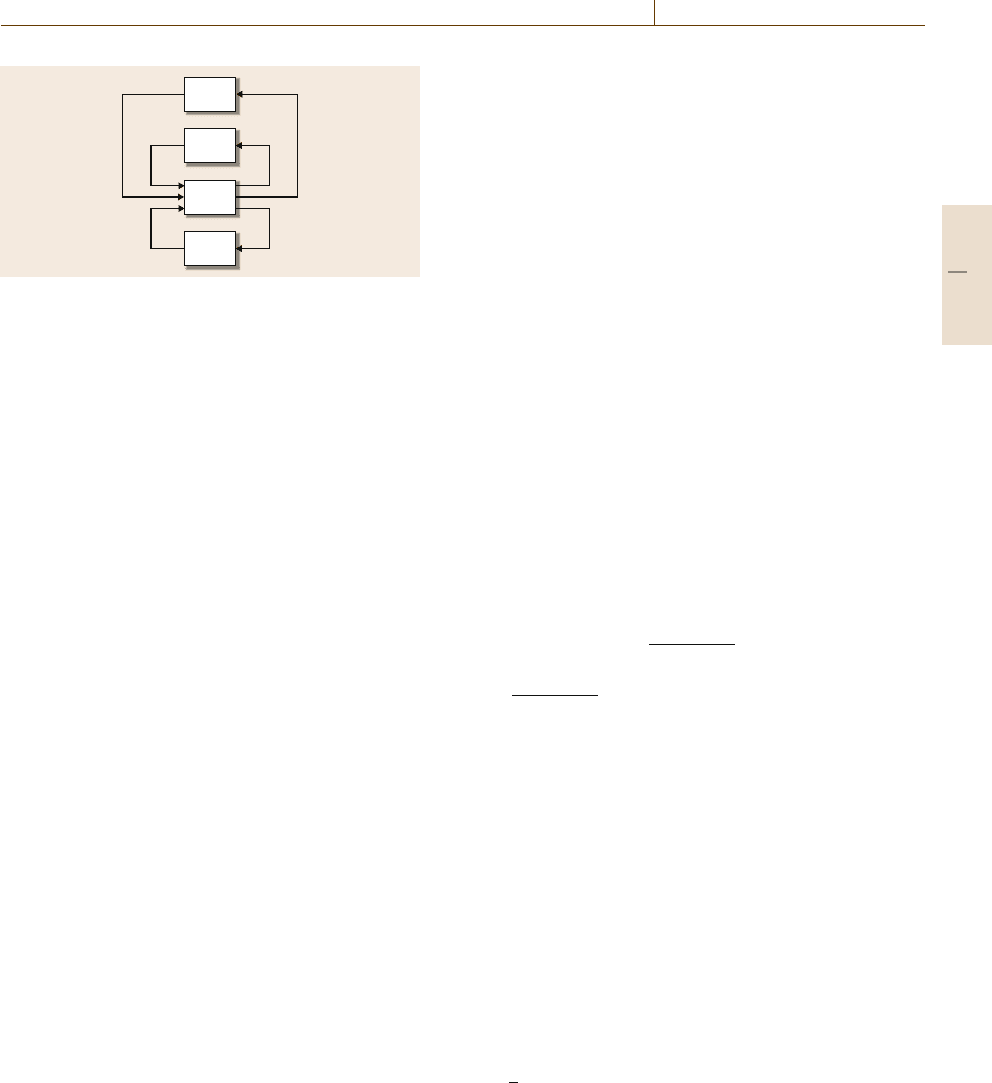
is still applied in parallel as Fig.10.18 shows. This stan-

dard model removes (s), as well as the K(s) controller

from the closed-loop system and lets P(s) represent the

(s)

K(s)

P(s)

Fig. 10.18 Standard model of control system extended by

uncertainties

rest of the components. It may involve additional output

signals (z) and a set of externalsignals (w) includingthe

set point.

Using a priori knowledge on the plant the concept

of the uncertainty modeling can further be improved.

Separating identical and independent technological

components into groups the perturbations can be ex-

pressed as structured uncertainties

(s) =diag[

(s), 

(s),...,

(s)], where



(s)

∞

≤1 i =1...r .

Structured uncertainties clearly lead to less conserva-

tive design as the unstructured uncertainties may want

to take care of perturbations never occurring in practice.

Consider the following control system (Fig.10.19)

as one possible realization of the standard model shown

in Fig.10.18. As a matter of fact here the common

form of the perturbations is used. Derivation is also

straightforward from the standard form of Fig. 10.18

with z =0 and w =r. Handling the nominal plant and

the feedback as one single unit described by R(s) =[I+

K(s)G

(s)]

−1

K(s), condition for the robust stability can

easily be derived by applying the small gain theorem

(Fig.10.20). The small gain theorem is the most funda-

mental result in robust stabilization under unstructured

perturbations. According to the small gain theorem any

closed-loop system consisting of two stable subsystems

(s)andG

(s) results in stable closed-loop system

provided that

G

(iω)

∞

G

(iω)

∞

< 1 .

(s)Δ(s)W

(s)

(s)K(s)

–

Fig. 10.19 Control system with uncertainties

Part B 10.6

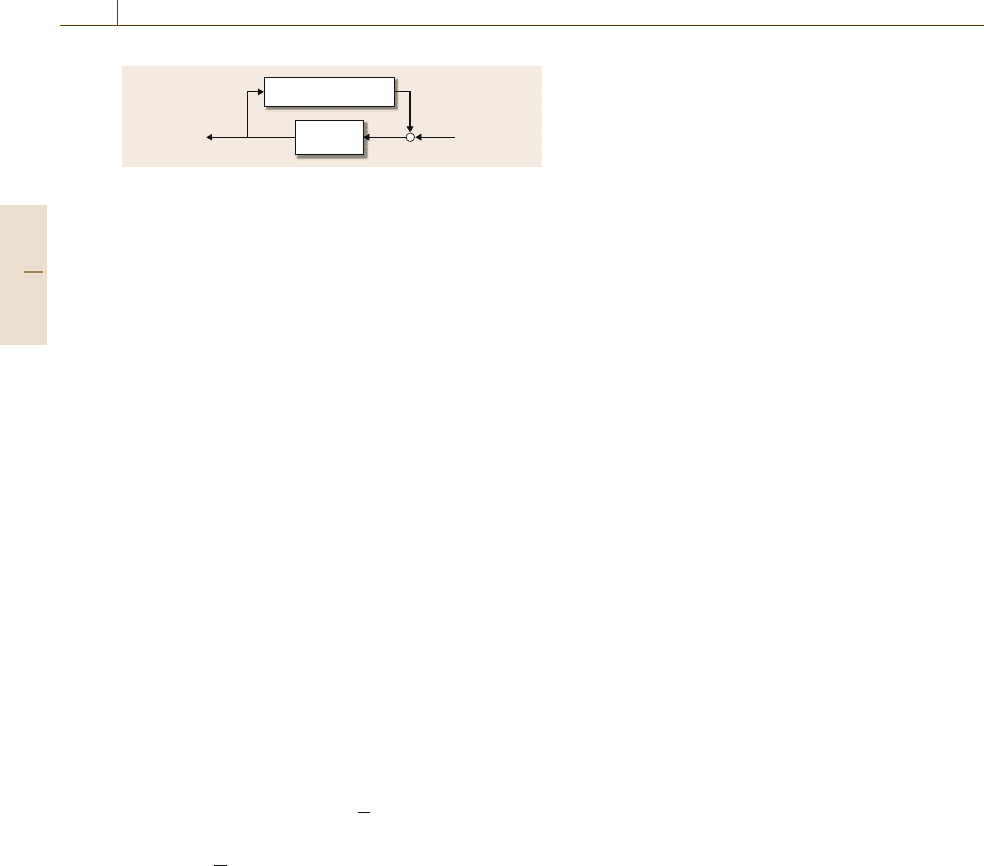
188 Part B Automation Theory and Scientiﬁc Foundations

R(s)

(s)Δ

(s)W

(s)

–

Fig. 10.20 Reduced control system with uncertainties

Applying the small gain theorem to the stabil-

ity analysis of the system shown in Fig.10.20,the

condition

W

(iω)R(iω)W

(iω)(iω)

∞

< 1

guarantees closed-loop stability. As

W

(iω)R(iω)W

(iω)(iω)

∞

≤

W

(iω)R(iω)W

(iω)

∞



∞

and

(iω)

∞

≤1 ,

thus the stability condition reduces to

W

(iω)R(iω)W

(iω)

∞

< 1 .

To support the closed-loop design procedure for

robust stability introduce the γ -norm W

(iω)R(iω)

(iω) (iω)

∞

=γ<1. Finding K(s) such that the

γ -norm is kept at its minimum the maximally stable

robust controller can be constructed.

The performance of a closed-loop system can be

rather conservative in case of having structural infor-

mation on the uncertainties. To avoid this drawback in

the design procedure the so-called structural singular

value is used instead of the H

∞

norm (being equal to the

maximum of thesingular value). The structuredsingular

value of a matrix M is deﬁned as

(M)=



min(k|det(I−kMΔ) =0

for structured Δ,

σ(Δ) ≤1)



−1

where Δ has a block-diagonal form of Δ = diag(...

...)andσ (Δ) ≤1. This deﬁnition suggests the fol-

lowing interpretation: a large value of μ

(M) indicates

that even a small perturbation can make the I−MΔ

matrix singular. On the other hand a small value of

(M) represents favorable conditions in this sense.

The structured singular value can be considered as the

generalization of the maximal singular value [10.6,13].

Using the notion of the structured singular value the

condition for robust stability (RS) can be formulated

as follows. Robust stability of the closed-loop system

is guaranteed if the maximum of the structured singu-

lar value of W

(iω)R(iω)W

(iω) lies within the unity

uncertainty radius

sup

(iω)R(iω)W

(iω)) < 1 .

Designing robust control systems is a far more in-

volved task than testing robust stability. The design

procedure minimizing the supremum of the structured

singular value is called structured singular value syn-

thesis or μ-synthesis. At this moment there is no direct

method to synthesize a μ-optimal controller. Related

algorithms to perform the minimization are discussed

in the literature under the term DK-iteration [10.6].

In [10.6] not only a detailed discussion is presented,

but also a MATLAB program is shown to provide bet-

ter understanding of the iterations to improve the robust

performance conditions.

So far therobuststability issuehas been discussed in

this section. It has been shown that the closed-loop sys-

tem remains stable, i. e., it is robustly stable, if stability

is guaranteed for all possible uncertainties. In a simi-

lar way, the notion of robust performance (RP)istobe

worked out. The closed-loopsystem exhibits robust per-

formance if the performance measures are kept within

a prescribed limit even for all possible uncertainties,

including the worst case, as well. Design considera-

tions for the robust performance have been illustrated

in Fig.10.18.

As the system performance is represented by the

signal z, robust performance analysis is based on inves-

tigating the relation between the external input signal w

and the performance output z

z = F[G(s), K(s), Δ(s)]w .

Deﬁning a performance measure on the transfer func-

tion matrix F[G(s), K(s), Δ(s)] by

J[F(G, K, Δ)]

the performance of the transfer function from the ex-

ogenous inputs w and to outputs z can be calculated.

The maximum of the performance – even in the worst

case possibly delivered by the uncertainties – can be

evaluated by

sup

{J[F(G, K, Δ)]:Δ

∞

< 1}.

Based on this value the robust performance of the sys-

tem can be judged. If the robust performance analysis is

to be performed in H

∞

sense, the measure to be applied

∞

=F[G(iω), K(iω), Δ(iω)]

∞

In this case the prespeciﬁed performance can be normal-

ized and the limit can be selected as 1. So equivalently,

the robust performance requirement can be formulated

Part B 10.6

Control Theory for Automation – Advanced Techniques 10.7 General Optimal Control Theory 189

(s)

K(s)

P(s)

Fig. 10.21 Design for robust performance traced back to

robust stability

F[G(iω), K(iω), Δ(iω)]

∞

< 1 ,

∀Δ(iω)

∞

≤1 .

Robust performance analysis can formally be traced

back to robust stability analysis. In this case a ﬁctitious

uncertainty block representing the nominal perfor-

mance requirements should be inserted across w and z

(Fig.10.21). Then introducing the



0 Δ



matrix of the uncertainties gives a pleasant way to trace

back the robust performance problem to the robust sta-

bility problem.

If robust performance synthesis is used the per-

formance measure must be minimized. In this case

μ-optimal design problem can be solved as an extended

robust stability design problem.

10.7 General Optimal Control Theory

In the previous sections design techniques have been

presented to control linear or linearized plants. Min-

imization of L

, H

or H

∞

loss functions all resulted in

linear control strategies. In practice, however, both the

processes and the control actions are mostly nonlinear,

e.g., controlinputs are typically constrained or saturated

in various technologies, and time-optimal control needs

to alter the control input instantaneously.

To cover a wider class of control problems the con-

trol tasks minimizing loss functions can be formulated

in a more general framework [10.25–31]. Restricted to

deterministic problems consider the following process

to be controlled

x(t) = f(x(t), u(t), t) , 0 ≤t ≤ T ,

x(0): given ,

where x(t) denotes the state variables available for state

feedback, and u(t) is the control input. The control per-

formance is expressed via the loss function constructed

by penalizing terms V

and V

J = V

(x(T), T)+



V[x(t), u(t), t]dt .

Designing an optimal controller is equivalent to mini-

mize the above loss function.

Denote by J

∗

(x(t), t) the optimal value of the loss

function while the system is governed from an initial

state x(0) to a ﬁnal state x(T). The principle of dynamic

programming [10.32] determines the optimal control

law by

min

u∈U



V[x(t), u(t), t]+

∂J

∗

[x(t), t]

∂x



f[x(t), u(t), t]



=−

∂J

∗

[x(t), t]

∂t

where the optimal loss function satisﬁes

∗

[x(T), T]=V

[x(T), T].

The equation of the optimal control law is called the

Hamilton–Jacobi–Bellman (HJB) equation in the con-

trol literature.

Note that the L

and H

optimal control policiesdis-

cussed earlier can be regarded as the special case of the

dynamic programming, where the process is linear and

the loss function is quadratic, and moreover the control

horizon is inﬁnitely large and the control input is not

restricted. Thus the linear system

x(t) =Ax(t)+Bu(t)

with the loss function

J =

∞







x+u





requires the optimal control via state-variable feedback

u(t) =−R

−1



Px(t) ,

Part B 10.7

190 Part B Automation Theory and Scientiﬁc Foundations

–1

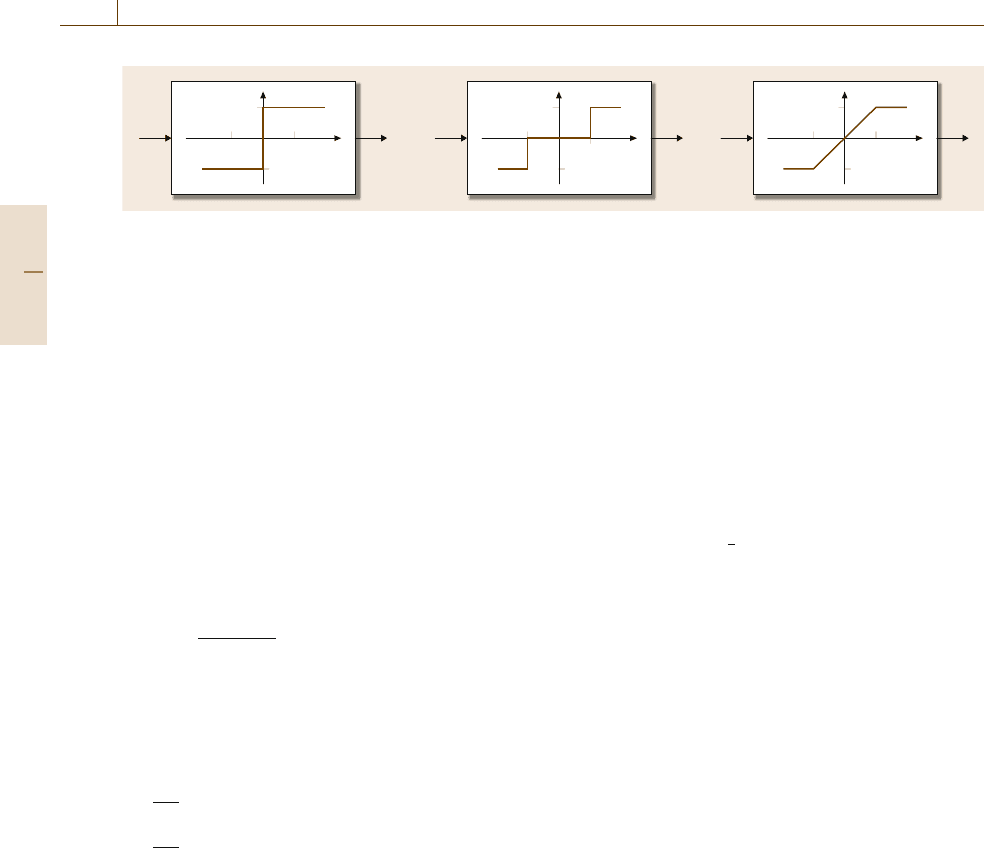
Fig. 10.22 Relay, relay with dead zone, and saturation function to be applied for each vector entry

where Q

≥0 and R

> 0, and ﬁnally the P matrix is

derived as the solution of the following algebraic Ric-

cati equation



P+PA −PBR

−1



P+Q

=0 .

At this point it is important to restate the importance

of stabilizability and detectability conditions. Without

satisfying these conditions, an optimizing controller

merely optimizes the cost functionand maynot stabilize

the closed-loop system. In particular, for the LQR prob-

lem just discussed, it is important to state that {A, B} is

stabilizable and {A, Q

1/2

} is detectable.

The HJB equation can be reformulated. To do so,

introduce the auxiliary variable λ(t) along the optimal

trajectory by

λ(t)=

∂J[x(t), t]

∂x

Apply λ(t) to deﬁne the following Hamiltonian function

H(x, u, t)=V(x, u, t)+λ



f(x, u, t) .

Then according to the Pontryagin minimum principle

∂H

∂λ

x(t) ,

∂H

∂x

=−

λ(t) ,

as well as

∗

(t) =argmin

u∈U

hold. (Note that if the control input is not restricted then

the last equation can be written as ∂H/∂u =0.)

Applying the minimum principle for time-invariant

linear dynamic systems with constrainedinput (|u

|≤1,

i =1...n

), various loss functions will lead to special

optimal control laws. Having the Hamiltonian function

in a general form of

H(x, u) =V(x, u)+λ



(Ax+Bu) ,

various optimal control strategies can be formulated by

assigning suitable V(x(t), t) loss functions:

•

If the goal is to achieve minimal transfer time, then

assign V(x, u) =1.

•

If the goal is to minimize fuel consumption, then

assign V(x, u) =u



sign(u).

•

If the goal is to minimize energy consumption, then

assign V(x, u) =



Then the application of the minimum principle provides

closed forms for the optimal control, namely:

•

Minimal transfer time requires u

(t) =−sign(B



λ)

(relay control)

•

Minimal fuel consumption requires u

(t) =−sgzm



λ) (relay with dead zone)

•

Minimal energy consumption requires u

(t) =

−sat(B



λ) (saturation).

These examples clarify that even for linear systems the

optimal control policies can be (and typically are) non-

linear. The nonlinear relations participating in the above

control laws are shown in Fig.10.22.

Dynamic programming is a general concept allow-

ing the exact mathematical handling of various control

strategies. Apart from the simplest cases, however, the

optimal control law needs demanding computer-aided

calculations. In the next section a special class of op-

timal controllers will be considered. These controllers

are called predictive controllers and they require re-

stricted calculation complexity, however, result in good

performance.

Part B 10.7

Control Theory for Automation – Advanced Techniques 10.8 Model-Based Predictive Control 191

10.8 Model-Based Predictive Control

As we have seen so far most control system design

methods assume a mathematical model of the process

to be controlled. Given a process model and knowl-

edge on the external system inputs the process output

can be predicted to some extent. To characterize the

behavior of the closed-loop system a combined loss

function can be constructed from the values of the pre-

dicted process outputs and that of the associated control

inputs. Control strategies minimizing this loss function

are called model-based predictive control (MPC). Re-

lated algorithms using special loss functions can be

interpreted as an LQ (linear quadratic) problem with

ﬁnite horizon. The performance of well-tuned predic-

tive control algorithms is outstanding for processes

with dead time. Speciﬁc model-based predictive control

algorithms are also known as dynamic matrix con-

trol (DMC), generalized predictive control (GPC), and

receding horizon control (RHC) [10.33–41]. Due to

the nature of the model-based control algorithms the

discrete-time (sampled-data) version of the control al-

gorithms will be discussed in the sequel. Also, most of

the detailed discussion is reduced for SISO systems in

this section.

The fundamental idea of predictive control can

be demonstrated through the DMC algorithm [10.40],

where the process output sample y(k+1) is predicted

by using all the available process input samples up to

the discrete time instant k (k = 0, 1, 2 ...) via a linear

function func

y(k +1) =func[u(k), u(k−1), u(k −2),

u(k −3),...] .

Repeating the above one-step-ahead prediction for fur-

ther time instants as

y(k +2) =func[u(k+1)

, u(k), u(k−1),

u(k −2),...] ,

y(k +3) =func[u(k+2), u(k+1), u(k),

u(k −1),...] ,

requires the knowledge of future control actions u(k +

1), u(k+2), u(k+3),..., as well. Introduce the free re-

sponse involving the future values of the process input

obtained provided no change occurs in the control input

at time k

∗

(k+1) =func[u(k) =u(k −1), u(k−1),

u(k −2), u(k−3),...] ,

∗

(k+2) =func[u(k +1) =u(k−1), u(k) =

u(k −1), u(k−1), u(k−2),...] ,

∗

(k+3) =func[u(k +2) =u(k−1), u(k+1) =

u(k −1), u(k) =u(k −1), u(k−1),...] ,

Using the free response just introduced above the pre-

dicted process outputs can be expressed by

y(k +1) =s

Δu(k)+y

∗

(k+1)

y(k +2) =s

Δu(k +1)+s

Δu(k)+y

∗

(k+2)

y(k +3) =s

Δu(k +2)+s

Δu(k +1)+s

Δu(k)

∗

(k+3) ,

where

Δu(k +i) =u(k+i)−u(k+i −1) ,

and s

denotes the i-th sample of the discrete-time-step

response of the process. Now a more compact form of

Predicted value =Forced response+Free response

is looked for in vector/matrix form

⎛

⎜

⎝

y(k +1)

y(k +2)

y(k +3)

⎞

⎟

⎠

⎛

⎜

⎝

00...

0 ...

...

⎞

⎟

⎠

⎛

⎜

⎝

Δu(k)

Δu(k +1)

Δu(k +2)

⎞

⎟

⎠

⎛

⎜

⎝

∗

(k+1)

∗

(k+2)

∗

(k+3)

⎞

⎟

⎠

Part B 10.8

192 Part B Automation Theory and Scientiﬁc Foundations

Apply here the following notations

S =

⎛

⎜

⎝

00...

0 ...

...

⎞

⎟

⎠

Y =[

y(k +1),

y(k +2),

y(k +3),...]



ΔU =[Δu(k), Δu(k+1), Δu(k+2),...]



∗

=[y

∗

(k+1), y

∗

(k+2), y

∗

(k+3),...]



Utilizing these notations

Y = SΔU +Y

∗

holds. Assuming that the reference signal (set point)

ref

(k) is available for the future time instants, deﬁne

the loss function to be minimized by



i=1



ref

(k+i)−

y(k +i)



If no restriction for the control signal is taken into ac-

count the minimization leads to

ΔU

opt

−1



ref

−Y

∗



where Y

ref

has been constructed from the samples of the

future set points.

The receding horizon control concept utilizes only

the very ﬁrst element of the ΔU

opt

vector according to

Δu(k) =1ΔU

opt

where 1 =(1, 0, 0,...). Observe that RHC needs to re-

calculate Y

∗

and to update ΔU

opt

in each step. The

application of the RHC algorithm results in zero steady-

state error; however, it requires considerable control

effort while minimizing the related loss function.

Smoothing in the control input can be achieved:

•

By extending the loss function with another compo-

nent penalizing the control signal or its change

•

By reducing the control horizon as follows

ΔU =[Δu(k), Δu(k+1), Δu(k+2),...,

Δu(k +N

−1), 0, 0,...,0]



Accordingly, deﬁne the loss function by



i=1



ref

(k+i)−

y(k +i)



+λ



i=1

[u(k +i)−u(k +i −1)]

then the control signal becomes

Δu(k) =1(S



S+λI)

−1





ref

−Y

∗



where

S =

⎛

⎜

⎝

0 ... 00

... 00

−1

−2

... s

−N

−1

... s

−N

⎞

⎟

⎠

All the above relations can easily be modiﬁed to cover

the control of processes with known time delay. Simply

replace y(k+1) by y(k+d+1) to consider y(k+d+1)

as the earliest sample of the process output effected by

the control action taken at time k, where d > 0 repre-

sents the discrete time delay.

As the idea of the model-based predictive control

is quite ﬂexible, a number of variants of the above dis-

cussed algorithms exist. The tuning parameters of the

algorithm are the prediction horizon N

, the control

horizon N

,andtheλ penalizing factor. Predictions re-

lated to disturbances can also be included. Just as an

example, a loss function



Y −Y

ref







Y −Y

ref





can be assigned to incorporate weighting matrices W

and W

, respectively, and a reduced version of the con-

trol signals can be applied according to

U = T

where T

is an a priori deﬁned matrix typically con-

taining zeros and ones. Then minimization of the loss

function results in

Δu(k) =1T







−1



ref

−Y

∗

) .

Constraints existing for the control input opena new

class for the control algorithms. In this case a quadratic

programming problem (conditional minimization of

a quadratic loss function to satisfy control constraints

represented by inequalities) should be solved in each

step. In detail, the loss function



Y −Y

ref







Y −Y

ref





is to be minimized again by U

, where

Y = ST

∗

Part B 10.8

Control Theory for Automation – Advanced Techniques 10.9 Control of Nonlinear Systems 193

under the constraint

Δu

min

≤Δu( j) ≤Δu

max

min

≤u( j) ≤u

max

The classical DMC approach is based on the sam-

ples of the step response of the process. Obviously, the

process model can also be represented by a unit impulse

response, a state-space model or a transfer function.

Consequently, beyond the controlinput, the process out-

put prediction can utilize the process output, the state

variables or the estimated state variables, as well. Note

that the original DMC is an open-loop design method

in nature, which should be extended by a closed-loop

aspect or be combined with an IMC-compatible con-

cept to utilize the advantages offered by the feedback

concept.

A further remark relates to stochastic process mod-

els. As an example, the generalized predictive control

concept [10.38,39] applies the model

A(q

−1

)y(k) = B(q

−1

)u(k −d)+

C(q

−1

)

where A(q

−1

), B(q

−1

), and C(q

−1

) are polynomials

of the backward shift operator q

−1

,andΔ = 1−q

−1

Moreover, ζ

is a discrete-time white-noise sequence.

Then the conditional expected value of the loss function



Y −Y

ref





(

Y −Y

ref

)+U





is to be minimized by U

. Note that model-based pre-

dictive control algorithms can be extended for MIMO

and nonlinear systems.

While LQ design supposing inﬁnite horizon pro-

vides stable performance, predictive control with ﬁnite

horizon using receding horizon strategy lacks stability

guarantees. Introduction of terminal penalty in the cost

function including the quadratic deviations of the states

from their ﬁnal values is one way to ensure stable per-

formance. Other methods leading to stable performance

with detailed stability analysis, as well as proper han-

dling of constraints, are discussed in [10.35, 36, 42],

where mainly sufﬁcient conditions have been derived

for stability.

For real-time applications fast solutions are re-

quired. Effective numerical methods to solve optimiza-

tion problems with reduced computational demand and

suboptimal solutions have been developed [10.33].

MPC with linear constraints and uncertainties can

be formulated as a multiparametric programming prob-

lem, which is a technique to obtain the solution of

an optimization problem as a function of the uncer-

tain parameters (generally the states). For the different

ranges of the states the calculation can be executed of-

ﬂine [10.33,43]. Different predictivecontrol approaches

for robust constrained predictive control of nonlinear

systems are also in the forefront of interest [10.33,

44].

10.9 Control of Nonlinear Systems

In this section results available for linear control sys-

tems will be extended for a special class of nonlinear

systems. For the sake of simplicity only SISO systems

will be considered.

In practice all control systems exhibit nonlinear

behavior to some extent [10.45, 46]. To avoid facing

problems caused by nonlinear effects linear models

around a nominal operating point are considered. In

fact, most systems work in a linear region for small

changes. However, at various operating points the lin-

earized models are different from each other according

to the nonlinear nature. In this section transformation

methods will be discussed making the operation of non-

linear dynamic systems linear over the complete range

of their operation. Clearly, this treatment, even though

the original process to be controlled remains nonlinear,

will allow us to apply all the design techniques de-

veloped for linear systems. As a common feature the

transformation methods developed for a special class

of nonlinear systems all apply state-variable feedback.

In the past decades a special tool, called Lie algebra,

was developed by mathematicians to extend notions

such as controllability or observability for nonlinear

systems [10.45]. The formalism offered by the Lie alge-

bra will not be discussed here; however, considerations

behind the application of this methodology will be

presented.

10.9.1 Feedback Linearization

Deﬁne the state vector x ∈ R

and the mappings

{f(x), g(x):

→R

} as functions of the state vector.

Then the Lie derivative of g(x)isdeﬁnedby

g(x)=

∂g(x)

∂x



f(x)

Part B 10.9

194 Part B Automation Theory and Scientiﬁc Foundations

and the Lie product of g(x)and f(x)isdeﬁnedby

g(x)=

∂g(x)

∂x



f(x)−

∂ f(x)

∂x



g(x)

= L

g(x)−

∂g(x)

∂x



f(x) .

Consider now a SISO nonlinear dynamic system

given by

x = f(x)+g(x)u ,

y =h(x) ,

where x = (x

, x

,...,x

)



is the state vector, u

is the input, and y is the output, while f, g,

and h are unknown smooth nonlinear functions with

{f(x), g(x):

→R

}, {h(x): R

→R},and f(0) =0.

The above SISO system has relative degree r at a point

if:

•

h(x) =0forallx in a neighborhood of x

and

for all k < r −1

•

r−1

h(x

) =0.

It can be shown that the above system equation can

be transformed to a form having identical structure for

the ﬁrst r entries

= z

r−1

= z

=a(z)+b(z)u ,

r+1

(z) ,

and

y = z

where the last n −r equations are called the zero dy-

namics. The above equation will be referred to later

on as canonical form, where the new state vector is

z = (z

, z

,...,z

)



. Using the Lie derivatives, a(z)

and b(z) can be found by

a(z) = L

r−1

h(x) ,

b(z) = L

h(x) .

The normal form related to the original system equa-

tions canbe deﬁnedby thediffeomorphism T as follows

= T

(x) = y =h(x) ,

= T

(x) =

y =

∂h

∂x



x = L

h(x) ,

= T

(x) = y

(r)

∂L

r−2

h(x)

∂x



x = L

r−1

h(x) .

Assuming that

h(x) =0 ,

r−2

h(x) =0 ,

all the remaining

r+1

(x),...,T

(x)

elements of the transformation matrix can be deter-

mined in a similar way. The geometric conditions for

the existence of such a global normal form have been

studied in [10.45].

Now, concerning the feedback linearization, the fol-

lowing result serves as a starting point for further

analysis: a nonlinearsystem withthe above assumptions

can be locally transformed into a controllable linear

system by state feedback. The transformation of coor-

dinates can be achieved if and only if

rank



g(x

), ad

g(x

),..., ad

n−1

g(x

)



at a given x

point and



g, ad

g,..., ad

n−2



is involutive near x

. Introducing

v =

and using the canonical form it is seen that the feedback

according to u =[v −a(z)]/b(z) results in a linear rela-

tionship between v and y in such a way that v is simply

the r-th derivative of y. In other words the linearizing

feedback establishes a relation from v to y equivalent to

r cascaded integrators. Note that the outputs of the in-

tegrators determine r states, while the remaining (n−r)

states correspond to the zero dynamics.

Part B 10.9