Nof S.Y. Springer Handbook of Automation

Подождите немного. Документ загружается.

Control Theory for Automation – Advanced Techniques 10.1 MIMO Feedback Systems 175

In the ﬁgure G(s) denotes the transfer function ma-

trix of the process and K(s) stands for the controller.

For the designer of the closed-loop system, G(s)is

given, while K(s) is the result of the design proce-

dure. Note that G(s) is only a model of the process

and serves here as the basis to design an appropriate

K(s). In practice the signals driving the control sys-

tem are delivered by a given process or technology

and the control input is in fact applied to the given

process.

The main design objectives are [10.2,6,13]:

•

Closed-loop and internal stability (just as it will be

addressed in this section)

•

Good command following (servo property)

•

Good disturbance rejection

•

Good measurement noise attenuation.

In addition, to keep operational costs low, small process

input values are preferred over large excursions in the

control signal. Also, as the controller design is based on

a model of the process, which always implies uncertain-

ties, design procedures aiming at stability and desirable

performance based on the nominal plant model should

be extended to tolerate modeling uncertainties as well.

Thus the list of the design objectives is to be completed

by:

•

Achieve reduced input signals

•

Achieve robust stability

•

Achieve robust performance.

Some of the above design objectives could be conﬂict-

ing; however, the performance-related issues typically

emerge in separable frequency ranges.

In thissection linear multivariable feedback systems

will be discussed with the following representations.

10.1.1 Transfer Function Models

Consider a linear process with n

control inputs ar-

ranged into a u ∈

input vector and n

outputs

arranged into a y ∈

output vector. Then the transfer

function matrix contains all possible transfer functions

between any of the inputs and any of the outputs

y(s) =

⎛

⎜

⎝

(s)

−1

(s)

⎞

⎟

⎠

=G(s)u(s)

⎛

⎜

⎝

1,1

(s) G

1,2

(s) ... G

1,n

(s)

−1,1

(s) G

−1,2

(s) ... G

−1,n

(s)

(s) G

(s) ... G

(s)

⎞

⎟

⎠

⎛

⎜

⎝

(s)

−1

(s)

⎞

⎟

⎠

where s is the Laplace operator and G

k,l

(s) denotes the

transfer function from the l-th component of the input

u to the k-th component of the output y. The trans-

fer function approach has always been an emphasized

modeling tool for control practice. One of the reasons is

that the G

k,l

(s) transfer functions deliver the magnitude

and phase frequency functions via a formal substitu-

tion of G

k,l

(s)



s=iω

= A

k,l

(ω)e

iφ

k,l

(ω)

. Note that for real

physical processes lim

ω→∞

k,l

(ω) =0. The transfer

function matrix G(s) is stable if each of its elements

is a stable transfer function. Also, the transfer function

matrix G(s) will be called proper if each of its elements

is a proper transfer function.

10.1.2 State-Space Models

Introducing n

state variables arranged into an x ∈R

state vector, the state-space model of a MIMO system is

given by the following equations

x(t) =Ax(t)+Bu(t) ,

y(t) =Cx(t)+Du(t) ,

where A ∈

×n

, B ∈ R

×n

,C ∈R

×n

,andD ∈

×n

are the system parameters [10.14,15].

Important notions (state variable feedback, control-

lability, stabilizability, observability and detectability)

have been introduced to support the deep analysis of

state-space models [10.1,2]. Roughly speaking a state-

space representationis controllable if anarbitrary initial

state can be moved to any desired state by suitable

choice of controlsignals. In terms of state-spacerealiza-

tions, feedback means state variable feedback realized

by a control law of u =−Kx, K ∈

×n

. Regarding

controllable systems, state variable feedback can relo-

cate all the poles of the closed-loop system to arbitrary

locations. If a system is not controllable, but the modes

(eigenvalues) attached to the uncontrollable states are

stable, the complete system is still stabilizable. A state-

space realization is said to be observable if the initial

Part B 10.1

176 Part B Automation Theory and Scientiﬁc Foundations

state x(0) can be determined from the output function

y(t), 0 ≤t ≤ t

ﬁnal

. A system is said to be detectable if

the modes (eigenvalues) attached to the unobservable

states are stable.

Using the Laplace transforms in the state-space

model equations the relation between the state-space

model and the transfer function matrix can easily be

derived as

G(s) =C(sI−A)

−1

B+D .

As far as the above relation is concerned the condition

lim

ω→∞

k,l

(ω) =0 raised for real physical processes

leads to D =0. Note that the G(s) transfer function con-

tains only the controllable and observable subsystem

represented by the state-space model {A, B, C, D}.

10.1.3 Matrix Fraction Description

Transfer functions can be factorized in several ways. As

matrices, in general, do not commute, the matrix frac-

tion description (MFD) form exists as a result of right

and left factorization, respectively [10.2,6,13]

G(s) =B

(s)A

−1

(s) =A

−1

(s)B

(s) ,

where A

(s), B

(s), A

(s), and B

(s) are all stable

transfer function matrices. In [10.2]itisshownthat

the right and left MFDs can be related to stabiliz-

able and detectable state-space models, respectively. To

outline the procedureconsider ﬁrstthe right matrix frac-

tion description (RMFD) G(s) =B

(s)A

−1

(s). For the

sake of simplicity the practical case of D = 0 will be

considered. Assuming that {A, B} is stabilizable, ap-

ply a state feedback to stabilize the closed-loop system

using a gain matrix K ∈

×n

u(t) =−Kx(t) ,

then the RMFD components can be derived in

a straightforward way as

(s) =C(sI−A+BK)

−1

B ,

(s) =I−K(sI−A+BK)

−1

B .

It can be shown that G(s) =B

(s)A

−1

(s) will not be

a function of the stabilizing gain matrix K,however,

the proof is rather involved [10.2]. Also, following the

above procedure, both B

(s)andA

(s) will be stable

transfer function matrices.

In a similar way, assuming that {A, C} is detectable,

apply a state observer to detect the closed-loop system

using a gain matrix L. Then the left matrix fraction

description (LMFD) components can be obtained as

(s) =C(sI−A+LC)

−1

B ,

(s) =I−C(sI−A+LC)

−1

L ,

being stable transfer function matrices. Again, G(s) =

−1

(s)B

(s) will be independent of L.

Concerning the coprime factorization, an important

relation, the Bezout identity, will be used, which holds

for the components of the RMFD and LMFD coprime

factorization



(s) Y

(s)

−B

(s) A

(s)



(s) −Y

(s)

(s) X

(s)





(s) −Y

(s)

(s) X

(s)



(s) Y

(s)

−B

(s) A

(s)



=I ,

where

(s) =K(sI−A+BK)

−1

L ,

(s) =I+C(sI−A+BK)

−1

L ,

(s) =K(sI−A+LC)

−1

L ,

(s) =I+K(sI−A+LC)

−1

B .

Note that the Bezout identity plays an important role

in control design. A good review on this can be found

in [10.1]. Also note that a MFD factorization can be

accomplished by using the Smith–McMillan form of

G(s) [10.1]. As a result of this procedure, however,

(s), B

(s), A

(s), and B

(s) will be polynomial ma-

trices. Moreover, both A

(s)andA

(s) will be diagonal

matrices.

10.2 All Stabilizing Controllers

In general, a feedback control system follows the struc-

ture shown in Fig.10.5, where the control conﬁguration

consists of two subsystems. In this general setup any

of the subsystems S

(s)orS

(s) may play the role of

the process or the controller [10.3]. Here {u

, u

} and

, y

} are multivariable external input and output sig-

nals in general sense, respectively. Moreover, S

(s)and

(s) represent transfer function matrices according to

(s) =S

(s)[u

(s)+y

(s)],

(s) =S

(s)[u

(s)+y

(s)].

Part B 10.2

Control Theory for Automation – Advanced Techniques 10.2 All Stabilizing Controllers 177

(s)

Fig. 10.5 A general feedback conﬁguration

Being restricted to linear systems the closed-loop

system is internally stable if and only if all the four

entries of the transfer function matrix



(s) H

(s)

(s) H

(s)



are asymptotically stable, where



(s)





(s)+y

(s)

(s)+y

(s)





(s) H

(s)

(s) H

(s)



(s)





[I−S

(s)S

(s)]

−1

[I−S

(s)S

(s)]

−1

(s)

[I−S

(s)S

(s)]

−1

(s) [I−S

(s)S

(s)]

−1





(s)



Also, from

(s) =u

(s)+y

(s) =u

(s)+S

(s)e

(s) ,

(s) =u

(s)+y

(s) =u

(s)+S

(s)e

(s) ,

we have







(s) H

(s)

(s) H

(s)



(s)





I −S

(s)

−S

(s) I



−1





P(s)

K(s)

Fig. 10.6 General control system conﬁguration

K(s)W

(s)

–

G(s)

(s)

Fig. 10.7 A sample closed-loop control system

so for internal stability we need the transfer function

matrix



[I−S

(s)S

(s)]

−1

[I−S

(s)S

(s)]

−1

(s)

[I−S

(s)S

(s)]

−1

(s) [I−S

(s)S

(s)]

−1





I −S

(s)

−S

(s) I



−1

to be asymptotically stable [10.13].

In the control system literature a more practical, but

still general closed-loop control scheme is considered,

as shown in Fig.10.6 with a generalized plant P(s)and

controller K(s) [10.6,13,14]. In this conﬁguration uand

y represent the process input and output, respectively, w

denotes external inputs (command signal, disturbance

or noise), z is a set of signals representing the closed-

loop performance in general sense. The controller K(s)

is to be adjusted to ensure a stable closed-loop system

with appropriate performance.

As an example Fig.10.7 shows a possible control

loop for tracking and disturbance rejection. Once the

disturbance signal d and the command signal (or set

point) signal r are combined to a vector-valuedsignal w,

the block diagram can easily be redrawn to match the

general scheme in Fig.10.6. Note the W

(s), W

(s),

and W

(s) ﬁlters introduced just to shape the system

performance. Since any closed-loop system can be re-

drawn to the general conﬁguration shown in Fig.10.5,

G(s)

K(s)

–

Fig. 10.8 Control system conﬁguration including set point

and input disturbance

Part B 10.2

178 Part B Automation Theory and Scientiﬁc Foundations

the block diagram in Fig. 10.8 will be considered in the

sequel.

Adopting the condition earlier developed for inter-

nal stability with S

(s) =G(s)andS

(s) =−K(s)it

is seen that now we need asymptotic stability for the

following four transfer functions



[I+K(s)G(s)]

−1

[I+K(s)G(s)]

−1

K(s)

−[I+G(s)K(s)]

−1

G(s) [I+G(s)K(s)]

−1



At the same time the block diagram of Fig. 10.8

suggests

e(s) =r(s)−y(s) =r(s)−G(s)K(s)e(s)

⇒e(s) =[I+G(s)K(s)]

−1

r(s) ,

whichleadsto

u(s) =K(s)e(s) =K(s)[I+G(s)K(s)]

−1

r(s)

=Q(s)r(s) ,

where

Q(s) =K(s)[I+G(s)K(s)]

−1

It can easily be shown that, in the case of a stable

G(s) plant, any stable Q(s) transfer function, in other

words Q parameter, results in internal stability. Rear-

ranging the above equation K(s) parameterized by Q(s)

exhibits all stabilizing controllers

K(s) =[I−Q(s)G(s)]

−1

Q(s) .

This result is known as the Youla parameteriza-

tion [10.13, 16]. Recalling u(s) = Q(s)r(s)andy(s) =

G(s)u(s) =G(s)Q(s)r(s) allows one to draw the block

diagram of the closed-loop system explicitly using Q(s)

(Fig.10.9). The control scheme shown in Fig.10.9 satis-

ﬁes u(s) =Q(s)r(s)andy(s) =G(s)Q(s)r(s), moreover

the process modeling uncertainties (G(s) of the phys-

ical process and G(s) of the model, as part of the

controller are different) are also taken into account.

This is the well-known internal model controller (IMC)

scheme [10.17,18].

Q(s)

–

Model

Controller

Plant

G(s)

Fig. 10.9 Internal model controller

A quick evaluation for the Youla parameterization

should point out a fundamental difference between de-

signing an overall transfer function T(s) from the r(s)

reference signal to the y(s) output signal using a nonlin-

ear parameterization by K(s)

y(s) =T(s)r(s) =G(s)K(s)[I+G(s)K(s)]

−1

r(s)

versus a design by

y(s) =T(s)r(s) =G(s)Q(s)r(s)

linear in Q(s).

Further analysis of the relation by y(s) =T(s)r(s) =

G(s)Q(s)r(s) indicates that Q(s) =G

−1

(s) is a reason-

able choice to achieve an ideal servo controller to ensure

y(s) =r(s). However, to intend to set Q(s) =G

−1

(s)is

not a practical goal for several reasons [10.2]:

•

Non-minimum-phase processes would exhibit un-

stable Q(s) controllers and closed-loop systems

•

Problems concerning the realization of G

−1

(s) are

immediately seen regarding processes with positive

relative degree or time delay

•

The ideal servo property would destroy the distur-

bance rejection capability of the closed-loop system

•

Q(s) =G

−1

(s) would lead to large control effort

•

Effects of errors in modeling the real process by

G(s) need further analysis.

Replacing the exact inverse G

−1

(s) by an approximated

inverse is in harmony with practical demands.

To discuss the concept of handling processes with

time delay consider single-input single-output (SISO)

systems and assume that

G(s) = G

(s)e

−sT

where G

(s) = B(s)/A(s) is a proper transfer function

with no time delay and T

> 0 is the time delay. Recog-

nizing that the time delaycharacteristics isnot invertible

y(s) = T

(s)e

−sT

r(s) =G

(s)Q(s)e

−sT

r(s)

can be assigned as the overall transfer function to

be achieved. Updating Fig.10.9 for G(s) = B(s)/

A(s)e

−sT

,Fig.10.10 illustrates the control scheme.

A key point is here, however, that the parameteriza-

tion by Q(s) should consider only G

(s) to achieve

(s)Q(s) speciﬁed by the designer. Note that, in the

model shown in Fig.10.10, uncertainties in G

(s)andin

the time delay should both be taken into account when

studying the closed-loop system.

Part B 10.2

Control Theory for Automation – Advanced Techniques 10.2 All Stabilizing Controllers 179

Q(s)

–

Model

Controller

Plant

B(s)

A(s)

–sT

B(s)

A(s)

–sT

Fig. 10.10 IMC control of a plant with time delay

K(s)

––

–

Model

Controller

Plant

B(s)

A(s)

–sT

B(s)

A(s)

–sT

Fig. 10.11 Controller using Smith predictor

The control scheme in Fig.10.10 has been im-

mediately derived by applying the Youla param-

eterization concept for processes with time delay.

The idea, however, of letting the time delay ap-

pear in the overall transfer function and restricting

the design procedure to a process with no time

delay is more than 50years old and comes from

Smith [10.19].

The fundamental concept of the design procedure

called the Smith predictor is to set up a closed-loop sys-

tem to control the output signal predicted ahead by the

time delay. Then, to meet the causality requirement, the

predicted output is delayed toderive thereal systemout-

put. All these conceptional steps can be summarized in

a control scheme; just redraw Fig.10.10 to Fig. 10.11

G(s)

Q(s)

(s)

(s)B

(s)

–1

(s)

–

Plant

–

G(s)

Q(s)

(s)

(s)A

(s)

–1

(s)

–

Plant

–

Fig. 10.12 Two different realizations of all stabilizing controllers for unstable processes

with

Q(s) = K(s)[I +G

(s)K(s)]

−1

The fact that the output of the internal loop can be

considered as the predicted value of the process output

explains the name of the controller. Note that the Smith

predictor is applicable for unstable processes as well.

In the case of unstable plants, stabilization of the

closed-loop system needs a more involved discussion.

In order to separate the unstable (in a more general

sense, the undesired) poles both the plant and the con-

troller transfer function matrices will be factorized to

(right or left) coprime transfer functions

G(s) =B

(s)A

−1

(s) =A

−1

(s)B

(s) ,

K(s) =Y

(s)X

−1

(s) =X

−1

(s)Y

(s) ,

where B

(s), A

(s), B

(s), A

(s), Y

(s), X

(s), Y

(s),

and X

(s) are all stable coprime transfer functions. Sta-

bility implies that B

(s) should contain all the right half

plane (RHP)-zeros of G(s), and A

(s) should contain

as RHP-zeros all the RHP-poles of G(s). Similar state-

ments are valid for the left coprime pairs. As far as the

internal stability analysis is concerned, assuming that

G(s) is strictly proper and K(s) is proper, the coprime

factorization offers the stability analysis via checking

the stability of



(s) −Y

(s)

(s) X

(s)



−1

and



(s) Y

(s)

−B

(s) A

(s)



−1

respectively. According to the Bezout identity [10.6,

13, 20] there exist X

(s)andY

(s) as stable transfer

function matrices satisfying

(s)A

(s)+Y

(s)B

(s) =I .

Part B 10.2

180 Part B Automation Theory and Scientiﬁc Foundations

G(s)

K(sI–A+LC)

–1

C(sI–A+LC)

–1

K(sI–A+LC)

–1

C(sI–A+LC)

–1

–

Q(s)

Plant

Fig. 10.13 State-space realization of all stabilizing controllers de-

rived from LMFD components

G(s)

C(sI–A+BK)

–1

C(sI–A+BK)

–1

K(sI–A+BK)

–1

K(sI–A+BK)

–1

–

Q(s)

Plant

Fig. 10.14 State-space realization of all stabilizing controllers de-

rived from RMFD components

G(s)

Q(s)

∫...dt

–

Plant

Fig. 10.15 State-space realization of all stabilizing controllers

In a similar way, a left coprime pair of transfer func-

tion matrices X

(s)andY

(s) can be found by

(s)Y

(s)+A

(s)X

(s) =I .

P(s)

Q(s)

J(s)

Fig. 10.16 General control system using Youla

parameterization

The stabilizing K(s) =Y

(s)X

−1

(s) =X

−1

(s)Y

(s)

controllers can be parameterized as follows. Assume

that the Bezout identity results in a given stabilizing

controller K =Y

(s)X

−1

(s) =X

−1

(s)Y

(s), then

(s) =X

(s)−B

(s)Q(s) ,

(s) =Y

(s)+A

(s)Q(s) ,

(s) =X

(s)−Q(s)B

(s) ,

(s) =Y

(s)+Q(s)A

(s) ,

delivers all stabilizing controllers parameterized by any

stable proper Q(s) transfer function matrix with appro-

priate size.

Though the algebra of the controller design proce-

dure may seem rather involved, in terms of block dia-

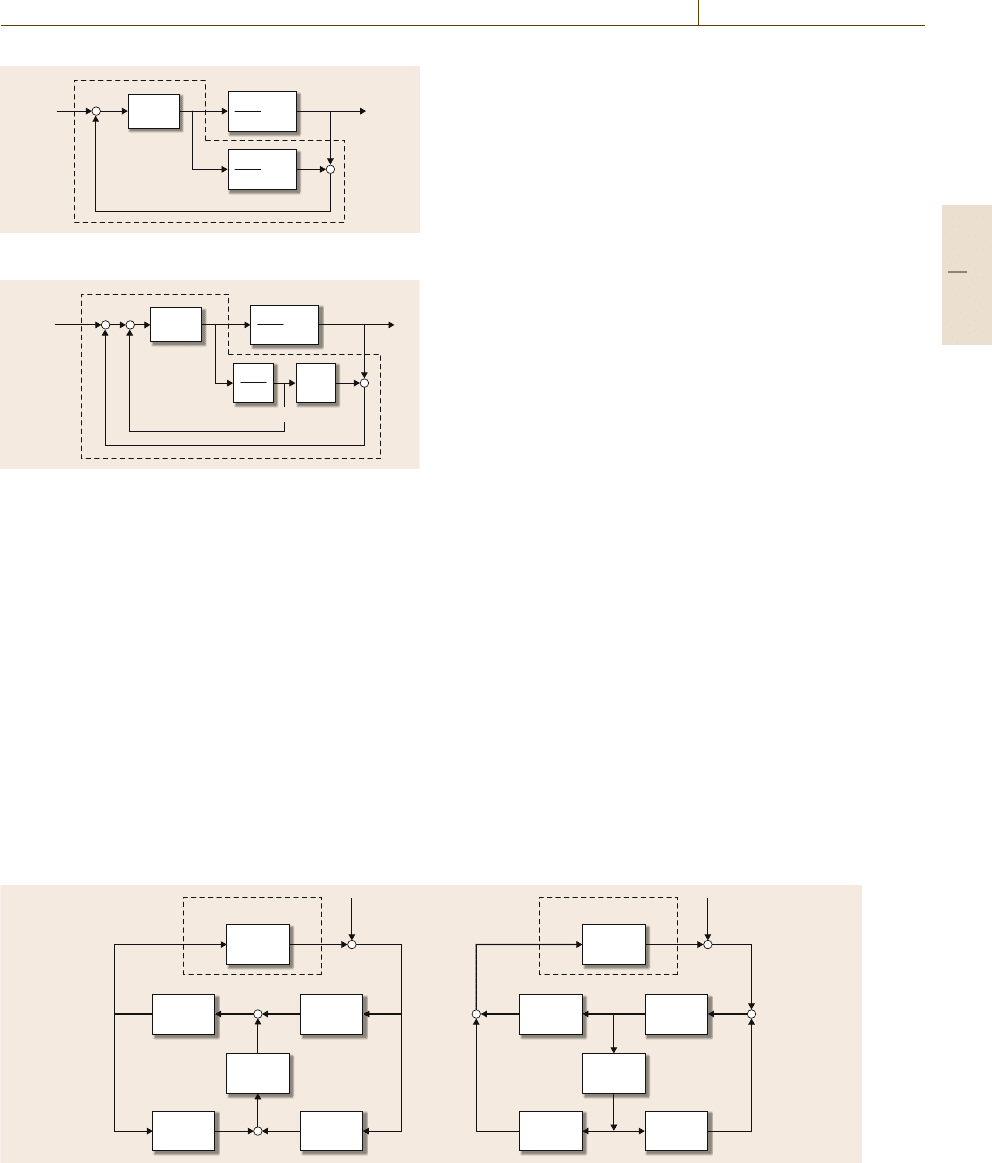
grams itcan be interpreted in severalways. In Fig.10.12

two possible realizations are shown to support the

reader in comparing the results obtained for unstable

processes with those shown earlier in Fig.10.9 to con-

trol stable processes.

Another obvious interpretationof the generaldesign

procedure can also be read out from the realizations

of Fig. 10.12. Namely, the immediate loops around

G(s) along Y

(s)andX

−1

(s) or along X

−1

(s)and

(s), respectively, stabilize the unstable plant, then

Q(s) serves the parameterization in a similar way as

originally introduced for stable processes.

Having the general control structure developed us-

ing LMFD or RMFD components (Fig. 10.12 gives

the complete review), respectively, we are in the po-

sition to show how the control of the state-space

model introduced earlier in Sect. 10.1 can be param-

eterized with Q(s). To visualize this capability recall

K(s) =X

−1

(s)Y

(s)and

(s) =C(sI−A+LC)

−1

B ,

(s) =I−C(sI−A+LC)

−1

L ,

Part B 10.2

Control Theory for Automation – Advanced Techniques 10.3 Control Performances 181

and apply these relations in the control scheme

of Fig.10.12 using LMFD components.

Similarly, recall K(s) =Y

(s)X

−1

(s)and

(s) =C(sI−A+BK)

−1

B ,

(s) =I−K(sI−A+BK)

−1

B ,

and apply these relations in the control scheme

of Fig.10.12 using RMFD components.

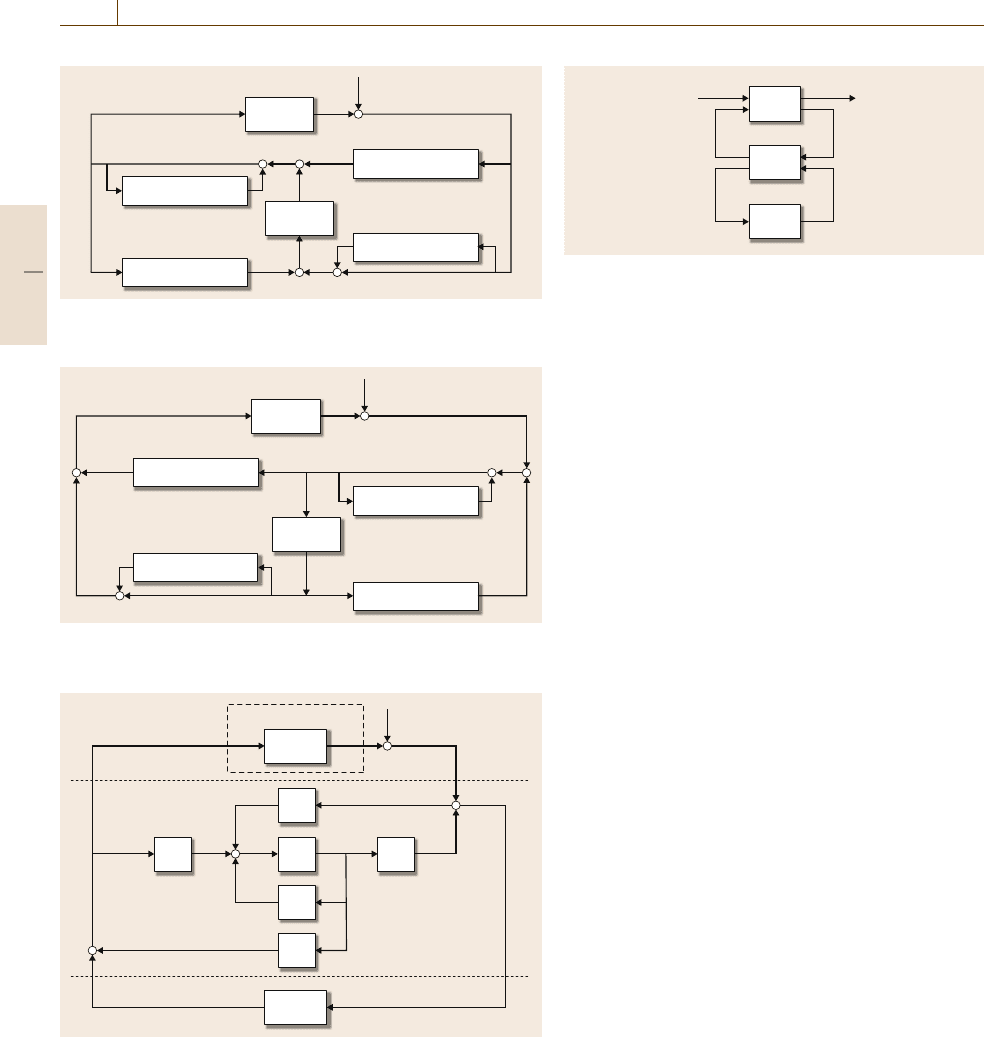
To complete the discussion on the various interpre-

tations of the all stabilizing controllers, observe that

the control schemes in Figs. 10.13 and 10.14 both use

4×n state variables to realize the controller dynamics

beyondQ(s). As Fig. 10.15 illustrates, equivalent reduc-

tion of the block diagrams of Figs. 10.13 and 10.14,

respectively, both lead to the realization of the all sta-

bilizing controllers. Observe that the application of the

LMFD and RMFD components lead to identical control

scheme.

In addition, any of the realizations shown in

Figs. 10.12–10.15 can directly be redrawn to form the

general control system scheme most frequently used

in the literature to summarize the structure of the

Youla parameterization. This general control scheme is

showninFig.10.16. In fact, the state-space realization

by Fig.10.15 follows the general control scheme shown

in Fig.10.16, assuming z = 0 and w =r. The transfer

function J(s) itself is realized by the state estimator

and state feedback using the gain matrices L and K,as

shownin Fig.10.15. Note that Fig. 10.16 can also be de-

rived from Fig.10.6 by interpreting J(s) as a controller

stabilizing P(s), thusallowingone toapply an additional

all stabilizing Q(s) controller.

10.3 Control Performances

So far we have derived various closed-loop structures

and parameterizations attached to them only to ensure

internal stability. Stability, however, is not the only is-

sue for the control system designer. To achieve goals

in terms of the closed-loop performance needs further

considerations [10.2,6,13,17]. Just to see an example:

in control design it is a widely posed requirement to

ensure zero steady-state error while compensating step-

like changes in the command or disturbance signals.

The practical solution suggests one to insert an inte-

grator into the loop. The same goal can be achieved

while using the Youla parameterization, as well. To il-

lustrate this action SISO systems will be considered.

Apply stable Q

(s)andQ

(s) transfer functions to form

Q(s) =sQ

(s)+Q

(s) .

Then Fig.10.9 suggests the transfer function between r

and r −y to be

1−Q(s)G(s) .

To ensure

1−[Q(s)G(s)]

s=0

we need

(s)(0) =[G(0)]

−1

Alternatively, using state models the selection accord-

ing to

Q(0) =1/[C(−A+BK+LC)

−1

will insert an integrator to the loop.

Several criteria exist to describe the required per-

formances for the closed-loop performance. To be able

to design closed-loop systems with various perfor-

mance speciﬁcations, appropriate norms for the signals

and systems involved should be introduced [10.13,

17].

10.3.1 Signal Norms

One possibility to characterize the closed-loop perfor-

mance is to integrate various functions derived from the

error signal. Assume that a generalized error signal z(t)

has been constructed. Then

z(t)



∞



|z|



1/v

deﬁnes the L

norm of z(t) with v as a positive integer.

The relatively easy calculations required for the

evaluations made the L

norm the most widely used cri-

terion in control. A further advantage of the quadratic

function is that energy represented by a given signal

can also be taken into account in this way in many

cases. Moreover, applying the Parseval’s theoremthe L

Part B 10.3

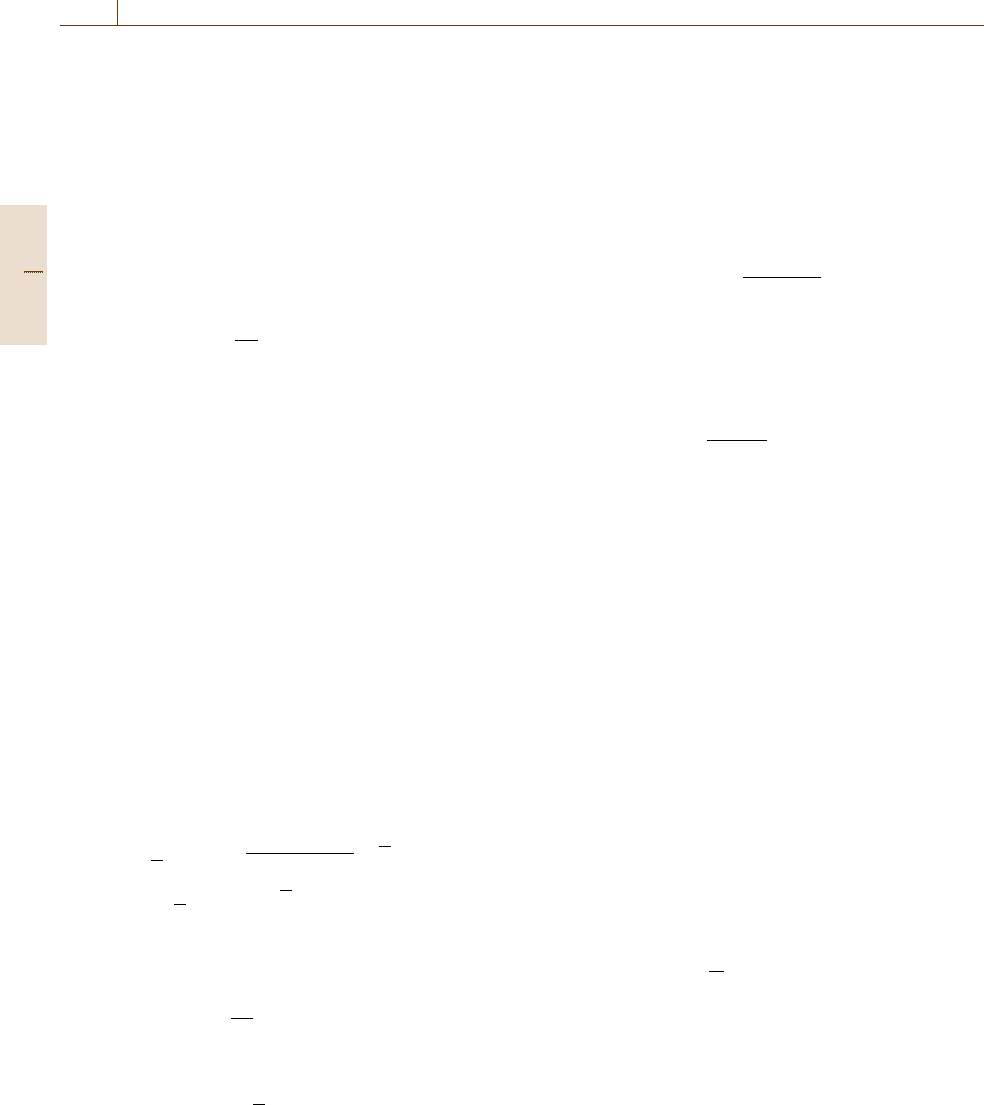
182 Part B Automation Theory and Scientiﬁc Foundations

norm can be evaluated using the signal described in the

frequency domain. Namely having z(s) as the Laplace

transform of z(t)

z(s) =

∞



z(t)e

−st

the Parseval’s theorem offers the following closed form

to calculate the L

norm as

z(t)

=z(s)



s=iω



=z(iω)

=



2π

∞



−∞

|z(iω)|

dω



1/2

Another important selection for v takes v →∞,which

results in

z(t)

∞

=sup

|z(t)|

and is interpreted as the largest or worst-case error.

10.3.2 System Norms

Frequency functions are extremely useful tools to an-

alyze and design SISO closed-loop control systems.

MIMO systems, however, exhibit an input-dependent,

variable gain at a given frequency. Consider a MIMO

system given by a transfer function matrix G(s)and

driven by an input signal w and delivering an output sig-

nal z. The norm z(iω)=G(iω)w(iω) of the system

output z depends on both the magnitude and direction

of the input vector w(iω), where ... denotes Eu-

clidean norm. The associated norms are therefore called

induced norms. Bounds for z(iω) are given by

(G(iω)) ≤

G(iω)w(iω)

w(iω)

≤

σ(G(iω)) ,

where σ

(G(iω)) and σ(G(iω)) denote the minimum and

maximum values of the singular values of G(iω), re-

spectively. The most frequently used system norms are

the H

and H

∞

norms deﬁned as follows

G



2π

∞



−∞

trace[G



(−iω)G(iω)]dω



1/2

and

G

∞

=sup

σ(G(iω)) .

It is clear that the system norms – as induced norms

– can be expressed by using signal norms. Introducing

g(t) as the unit impulse response of G(s) the Parseval’s

theorem suggests expressing the H

system norm by the

signal norm

G

∞



trace[g



(t)g(t)]dt .

Further on, the H

∞

norm can also be expressed as

G

∞

=sup

max



G(iω)w

w

where w =0

and w ∈



where w denotes a complex-valued vector. For a dy-

namic system the above expression leads to

G

∞

=sup



z(t)

w(t)

where w(t)

=0



if G(s) is stable and proper. The above expression

means that the H

∞

norm can be expressed by L

signal

norm.

Assume a linear system given by a state model

{A, B, C} and calculate its H

and H

∞

norms. Trans-

forming the state model to a transfer function matrix

G(s) =C(sI−A)

−1

the H

norm is obtained by

G

=trace(CP



) =trace(B



B) ,

where P

and P

are delivered by the solution of the

Lyapunov equations



+BB



=0 ,

A+A



C =0 .

The calculation of the H

∞

norm can be performed via

an iterative procedure, where in each step an H

norm

is to be minimized. Assuming a stable system, construct

the Hamiltonian matrix

H =





−C



C −A





For large γ the matrix H has n

eigenvalues with neg-

ative real part and n

eigenvalues with positive real

part. As γ decreases these eigenvalues eventually hit the

imaginary axis. Thus

G

∞

= inf

γ>0

(γ ∈ R: H hasnoeigenvalues

with zero real part) .

Part B 10.3

Control Theory for Automation – Advanced Techniques 10.4 H

Optimal Control 183

Note that each step within the γ -iteration procedure

is after all equivalent to solve an underlying Riccati

equation. The solution of the Riccati equation will be

detailed later on in Sect.10.4.

So far stability issues have been discussed and sig-

nal and system norms, as performance measures, have

been introduced to evaluate the overall operation of

the closed-loop system. In the sequel the focus will

be turned on design procedures resulting in both stable

operation and expected performance. Controller design

techniques to achieve appropriate performance mea-

sures via optimization procedures related to the H

and H

∞

norms will be discussed, respectively [10.6,

21].

10.4 H

Optimal Control

To start the discussion consider the general control sys-

tem conﬁguration shown in Fig.10.6 describe the plant

by the transfer function











or equivalently, by a state model

⎛

⎜

⎝

⎞

⎟

⎠

⎛

⎜

⎝

⎞

⎟

⎠

⎛

⎜

⎝

⎞

⎟

⎠

Assume that (A, B

) is controllable, (A, B

) is stabiliz-

able, (C

, A) is observable, and (C

, A) is detectable.

For the sake of simplicity nonsingular D



and



matrices, as well as D



=0 and D



will be considered.

Using a feedback via K(s)

u =−K(s)y ,

the closed-loop system becomes

z = F[G(s), K(s)]w ,

where

F[G(s), K(s)]=G

(s)−G

(s)[I+K(s)G

(s)]

−1

K(s)G

(s) .

Aiming at designing optimal control in H

sense the

=F(G(iω), K(iω))

norm is to be minimized by

a realizable K(s). Note that this control policy can be

interpreted as a special case of the linear quadratic

(LQ) control problem formulation. To show this rela-

tion assume aweighting matrix Q

assigned for thestate

variables and a weighting matrix R

assigned for the

input variables. Choosing



1/2



and D



1/2



and

z = C

x+D

as an auxiliary variable the well-known LQ loss func-

tion can be reproduced with



1/2





1/2

and R



1/2





1/2

Up to this point the feedback loop has been set up and

the design problem has been formulated to ﬁnd K(s)

minimizing J

=F(G(iω), K(iω))

. Note that the op-

timal controller will be derived as a solution of the

state-feedback problem. The optimization procedure is

discussed below.

10.4.1 State-Feedback Problem

If all the state variables are available then the state vari-

able feedback

u(t) =−K

x(t)

is used with the gain

=(D



)

−1



where P

represents the positive-deﬁnite or positive-

semideﬁnite solution of the



A−P







−1



Riccati equation. According to this control law the

A−B

matrix will determine the closed-loop stability.

As far as the solution of the Riccati equation is

concerned, an augmented problem setup can turn this

task to an equivalent eigenvalue–eigenvector decompo-

sition (EVD). In details, the EVD decomposition of the

Hamiltonian matrix

H =



A −B







−1



−C



−A





Part B 10.4

184 Part B Automation Theory and Scientiﬁc Foundations

will separate the eigenvectors belonging to stable and

unstable eigenvalues, then the positive-deﬁnite P

ma-

trix can be calculated from the eigenvectors belonging

to the stable eigenvalues. Denote  the diagonal ma-

trix containing the stable eigenvalues and collect the

associated eigenvectors to a block matrix





i.e.,









 .

Then it can be shown that the solution of the Riccati

equation is obtained by

=GF

−1

At the same time it should be noted that there exist

further, numerically advanced procedures to ﬁnd P

10.4.2 State-Estimation Problem

The optimal state estimation (state reconstruction) is

the dual of the optimal control task [10.1, 4]. The esti-

mated states are derived as the solution of the following

differential equation:

x(t) =A

x(t)+B

u(t)+L

[y(t)−C

x(t)],

where



)

−1

and the P

matrix is the positive-deﬁnite or positive-

semideﬁnite solution of the Riccati equation



+AP

−P









−1



=0 .

Note that the

A−P









−1

matrix characterizing the closed-loop system is stable,

i.e., all its eigenvalues are on the left-hand half plane.

Remark 1: Putting the problem justdiscussed so far into

a stochastic environment the above state es-

timation is also called a Kalman ﬁlter.

Remark 2: The gains L

∈ R

×n

and K

∈ R

×n

have been introduced and applied in earlier

stages in this chapter to create the LMFD

and RMFD descriptions, respectively. Here

their optimal values have been derived in H

sense.

∫ dt

–

∫ dt

–

Fig. 10.17 Duality of state control and state estimation

Remark 3: State control and state estimation exhibit

dual properties and share some common

structural features. Comparing Fig.10.17a

and b it is seen that the structure of the state

feedback control and that of the full order

observer resemble each other to a large ex-

tent. The output signal, as well as the L

and C matrices in the observer, play iden-

tical role as the control signal, as do the B

and K matrices in state feedback control.

Parameters in the matrices L and K are to

be freely adjusted for the observer and for

the state feedback control, respectively. In

a sense, calculating the controller and ob-

server feedback gain matrices represent dual

problems. In this case duality means that

any of the structures shown in Fig. 10.17a,b

can be turned to its dual form by revers-

ing the direction of the signal propagation,

interchanging the input and output signals

(u ↔ y), and transforming the summation

points to signal nodes and vice versa.

10.4.3 Output-Feedback Problem

If the state variables are not available for feedback the

optimal control law utilizes the reconstructed states. In

case of designing optimal control in H

sense the con-

trol law u(t) =−K

x(t) is replaced by u(t) =−K

x(t).

Part B 10.4