Nof S.Y. Springer Handbook of Automation

Подождите немного. Документ загружается.

Control of Uncertain Systems 11.3 Variable-Structure Neural Component 205

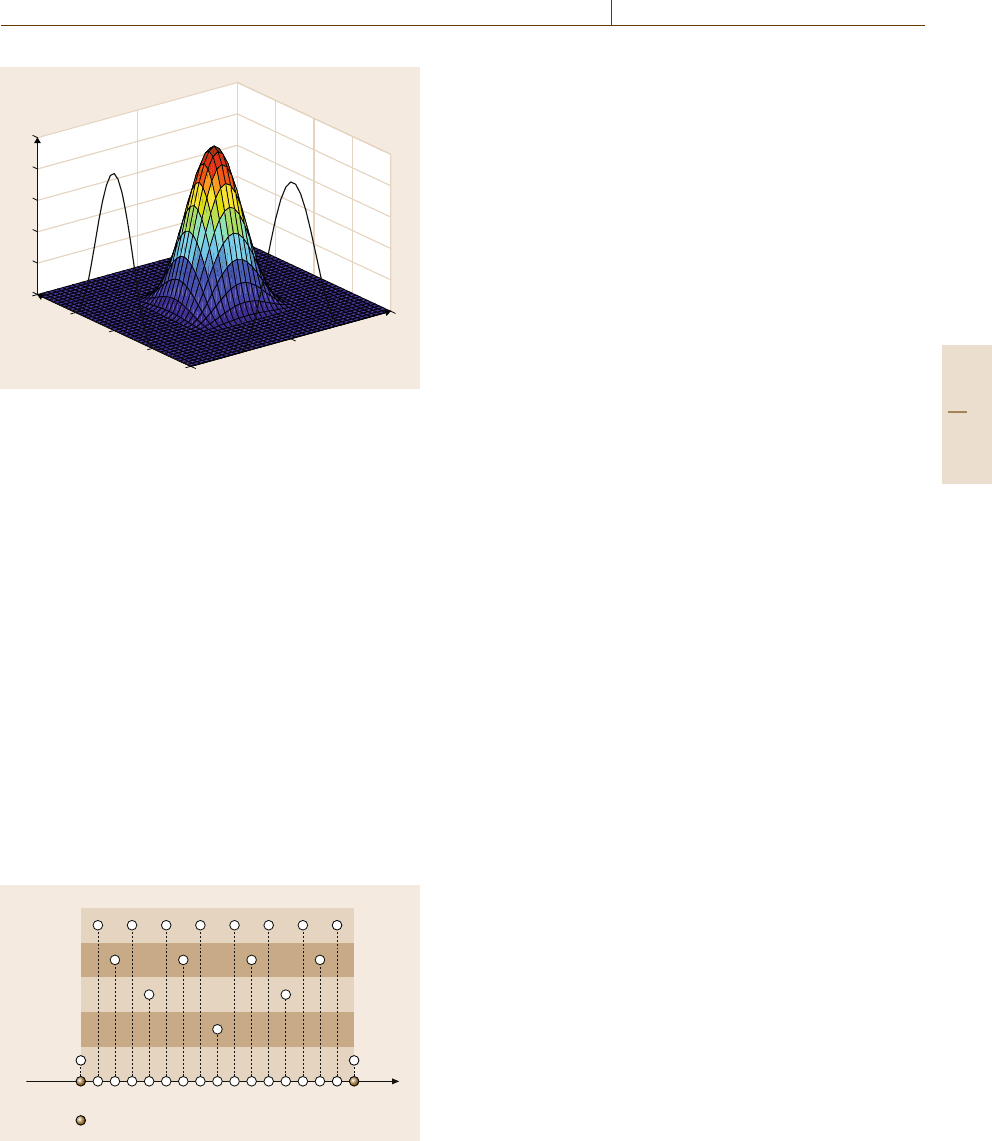
(x)

0.8

0.6

0.4

0.2

–1

–2

Fig. 11.3 Plot of a two-dimensional (2-D) raised-cosine ra-

dial basis function

11.3.1 Center Grid

Recall that the unknown functions are approximated

over a compact set Ω

⊂R

.ItisassumedthatΩ

can

be represented as



x ∈R

: x

≤ x ≤ x



(11.18)



x ∈R

: x

≤ x

, 1 ≤i ≤ n



, (11.19)

where the n-dimensional vectors x

and x

denote lower

and upper bounds of x, respectively. To locate the cen-

ters of RBFs inside the approximation region Ω

,an

n-dimensional center grid with layer hierarchy is uti-

lized, where each grid node corresponds to the center of

one RBF. The center grid is initialized with its nodes

located at (x

, x

)×(x

, x

)×···×(x

, x

), where

× denotes the Cartesian product. The 2

grid nodes of

the initial center grid are referred to as boundary grid

Potential grids nodes

Boundary nodes

Layer

Fig. 11.4 Example of determining potential grid nodes in

one coordinate

nodes and cannot be removed. Additional grid nodes

will be added and then can be removed within this

initial grid as the controlled system evolves in time.

The centers of new RBFs can only be placed at the

potential locations. The potential grid nodes are deter-

mined coordinate-wise. In each coordinate,the potential

grid nodes of the ﬁrst layer are the two ﬁxed bound-

ary grid nodes. The second layer has only one potential

grid node in the middle of the boundary grid nodes.

Then the potential grid nodes of the subsequent lay-

ers are in the middle of the adjacent potential grid

nodes of all the previous layers. The determination

of potential grid nodes in one coordinate is illustrated

in Fig.11.4.

11.3.2 Adding RBFs

As the controlled system evolves in time, the out-

put tracking error e is measured. If the magnitude of

e exceeds a predetermined threshold e

max

, and if the

dwelling time of the current network structure has been

greater than the prescribed T

, the network tries to add

new RBFs at potential grid nodes, that is, add new grid

nodes. First, the nearest-neighboring grid node, denoted

(nearest)

, to the current input x is located among existing

grid nodes. Then the nearer-neighboring grid node de-

noted c

(nearer)

is located, where c

i(nearer)

is determined

such that x

is between c

i(nearest)

and c

i(nearer)

.Next,

the adding operation is performed for each coordinate

independently.

In the i-th coordinate, if the distance between x

and c

i(nearest)

is smaller than a prescribed threshold

i(threshold)

or smaller than a quarter of the distance

between c

i(nearest)

and c

i(nearer)

, no new grid node is

added in the i-th coordinate. Otherwise, a new grid

node located at half of the sum of c

i(nearest)

and c

i(nearer)

is added in the i-th coordinate. The design parameter

i(threshold)

speciﬁes the minimum grid distance in the i-

th coordinate. The above procedures for adding RBFs

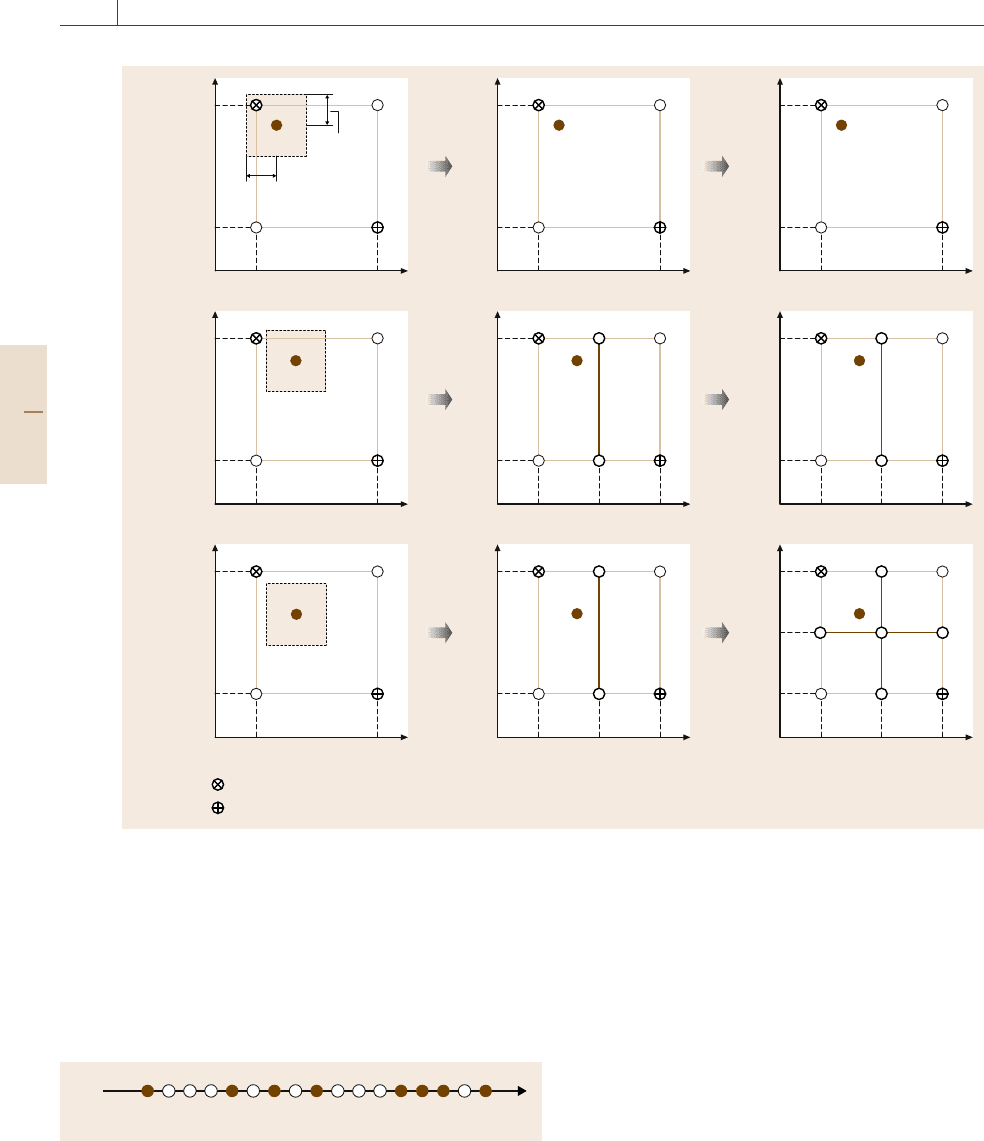
are illustrated with two-dimensional examples shown

in Fig. 11.5. In case 1, no RBFs are added. In case 2,

new grid nodes are added out of the ﬁrst coordinate. In

case 3, new grid nodes are added out of both coordi-

nates. In summary, a new grid node is added in the i-th

coordinate if the following conditions are satisﬁed:

1. |e| > e

max

2. The elapsed time since last operation, adding or re-

moving, is greater than T



−c

i(nearest)



> max





i(nearest)

−c

i(nearer)



/4, d

i(threshold)



Part B 11.3

206 Part B Automation Theory and Scientiﬁc Foundations

Case 1

2(nearest)

2(nearer)

1(nearer)

1(nearest)

1(threshold)

2(threshold)

2(nearest)

2(nearer)

1(nearer)

1(nearest)

2(nearest)

2(nearer)

1(nearer)

1(nearest)

Case 2

2(nearest)

2(nearer)

1(nearer)

1(nearest)

2(nearest)

2(nearer)

1(nearer)

1(nearest)

Case 3

The nearest-neighboring center c

(nearest)

The nearer-neighboring center c

(nearer)

2(nearest)

2(nearer)

1(nearer)

1(nearest)

2(nearest)

2(nearer)

1(nearer)

1(nearest)

New RBFs

out of first

coordinate

New RBFs

out of first

coordinate

No new RBFs

out of first

coordinate

2(nearest)

2(nearer)

1(nearer)

1(nearest)

No new

RBFs out of

second coordinate

No new RBFs

out of second

coordinate

2(nearest)

2(nearer)

1(nearer)

1(nearest)

New RBFs

out of

second

coordinate

Fig. 11.5 Two-dimensional examples of adding RBFs

The layer of the i-th coordinate assigned to the newly

added grid node is one level higher than the highest

layer of the two adjacent existing grid nodes in the same

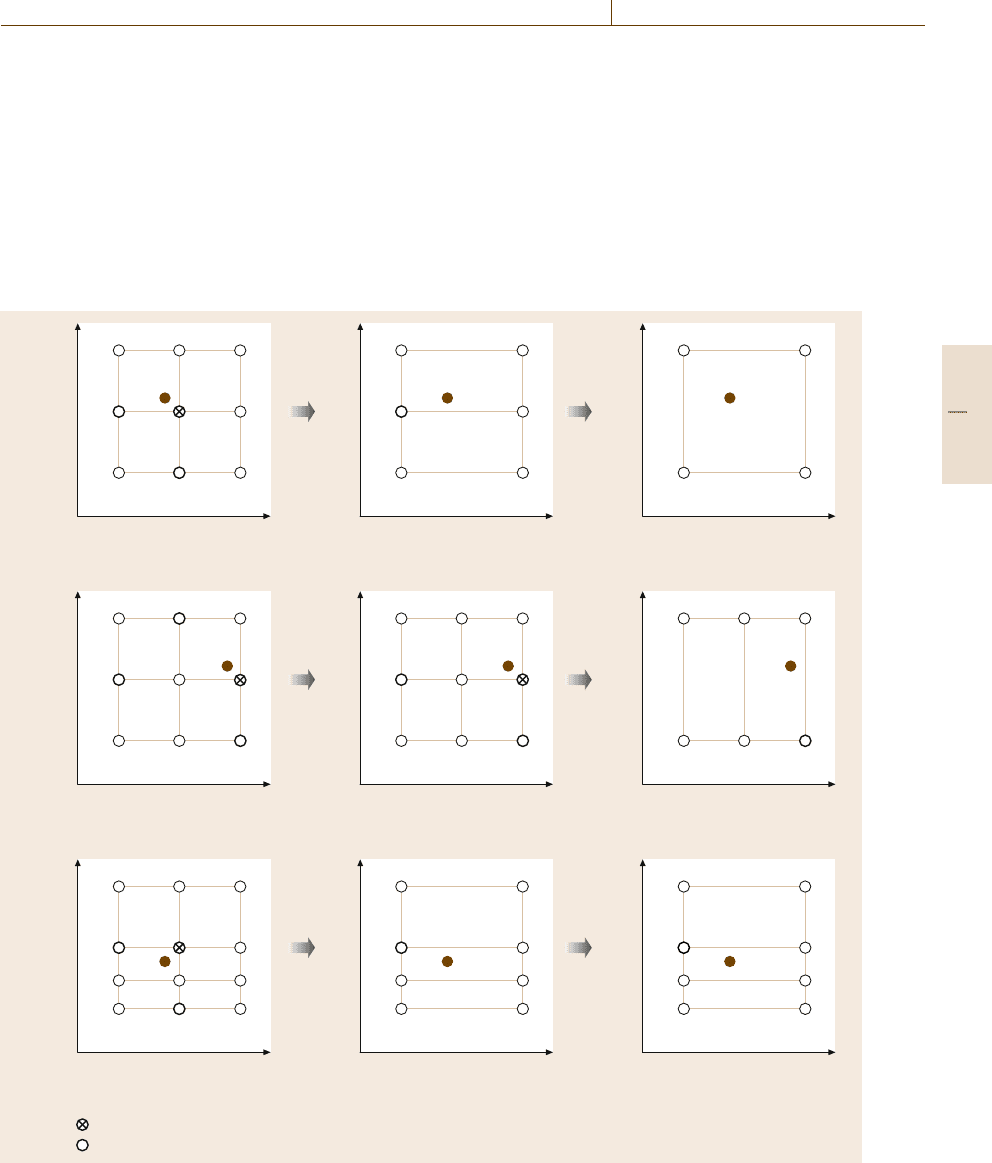
coordinate. A possiblescenario of formationof the layer

hierarchy in one coordinate is shown in Fig.11.6. The

white circles denote potential grid nodes, and the black

circles stand for existing grid nodes. The number in

Layer No.1 5 4 5 3 5 4 5 2 5 4 5 3 5 4 5 1

13524761

Fig. 11.6 Example of formation of the layer hierarchy in one coor-

dinate

the black circles shows the order in which the corre-

sponding grid node is added. The two black circles with

number 1 are the initial grid nodes in this coordinate,

so they are in the ﬁrst layer. Suppose the adding oper-

ation is being implemented in this coordinate after the

grid initialization. Then a new grid node is added in the

middle of two boundary nodes 1 – see the black cir-

cle with number 2 in Fig.11.6. This new grid node is

assigned to thesecond layer becauseof theresulting res-

olution it yields. Then all the following grid nodes are

added one by one. Note that nodes 3 and 4 belong to the

same third layer because they yield the same resolution.

On the other hand, node 5 belongs to the fourth layer

because it yields higher resolution than nodes 2 and 3.

Part B 11.3

Control of Uncertain Systems 11.3 Variable-Structure Neural Component 207

Nodes 6 and 7 are assigned to their layers in a similar

fashion.

11.3.3 Removing RBFs

When the magnitude of the output tracking error e

falls within the predetermined threshold e

max

and the

dwelling-time requirement has been satisﬁed, the net-

work attempts to remove some of the existing RBFs,

that is, some of the existing grid nodes, in order to avoid

Layer No. 1 2 1

Layer No.

Remove RBFs

out of first

coordinate

RBFs not removed

out of first coordinate

Remove RBFs

out of first coordinate

Remove RBFs

out of

second

coordinate

RBFs not removed

out of second

coordinate

Remove RBFs

out of second

coordinate

Case 1: All conditions are satisfied for both coordinates

Layer No. 1 1

Layer No. 1 2 1

Layer No. 1

Case 2: The third condition is not satisfied for the first coordinate

Layer No. 1 1

Layer No. 1

333

Layer No. 1

Case 3: The fourth condition is not satisfied for the second coordinate

Layer No. 1 1

The nearest-neighboring center c

(nearest)

The gride node in the i-th coordinate with its i-th coordinate to be c

i(nearest)

Fig. 11.7 Two-dimensional examples of removing RBFs

network redundancy. The RBF removing operation is

also implemented for each coordinate independently. If

i(nearest)

is equal to x

or x

, then no grid node is

removed from the i-th coordinate. Otherwise, the grid

node located at c

i(nearest)

is removed from the i-th coor-

dinate if this grid node is in the higher than or in the

same layer as the highest layer of the two neighbor-

ing grid nodes in the same coordinate, and the distance

between x

and c

i(nearest)

is smaller than a fraction τ

of the distance between c

i(nearest)

and c

i(nearer)

, where

Part B 11.3

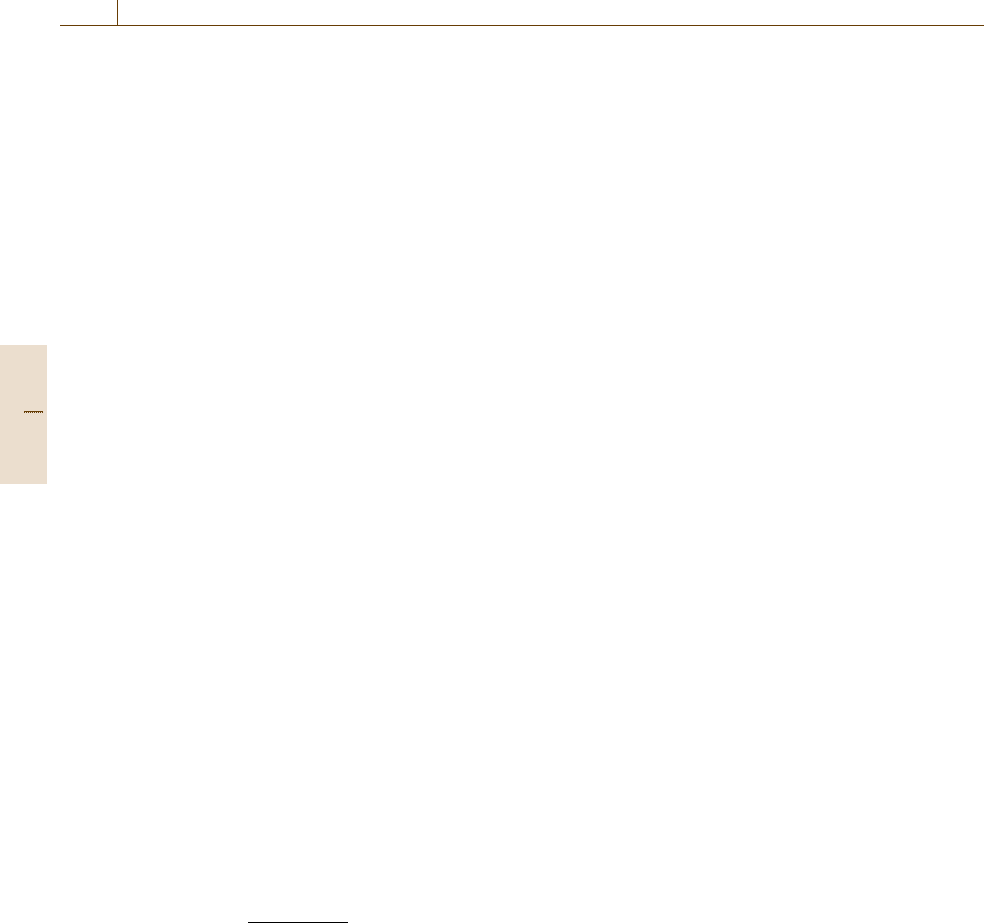
208 Part B Automation Theory and Scientiﬁc Foundations

the fraction τ is a design parameter between 0 and 0.5.

The above conditionsfor the removing operation to take

place in the i-th coordinate can be summarized as:

1. |e|≤e

max

2. The elapsed time since last operation, adding or re-

moving, is greater than T

3. c

i(nearest)

/∈



, x



4. The grid node in the i-th coordinate with its coordi-

nate equal to c

i(nearest)

is in a higher than or in the

same layer as the highest layer of the two neighbor-

ing grid nodes in the same coordinate.



−c

i(nearest)



<τ



i(nearest)

−c

i(nearer)



, τ ∈(0, 0.5).

Two-dimensional examples of removing RBFs are illus-

trated in Fig.11.7, where the conditions (1), (2), and (5)

are assumed to be satisﬁed for both coordinates.

11.3.4 Uniform Grid Transformation

The determination of the radius of the RBF is much eas-

ier in a uniform grid than in a nonuniform grid because

the RBF is radially symmetric with respect to its cen-

ter. Unfortunately, the center grid used to locate RBFs

is usually nonuniform. Moreover, the structure of the

center grid changes after each adding or removing oper-

ation, which further complicates the problem. In order

to simplify the determination of the radius, the one-

to-one mapping z(x) =[z

), z

),...,z

)]



proposed in [11.60], is used to transform the center grid

into a uniform grid. Suppose that the self-organizing

RBF network is now with the v-th admissible struc-

ture after the adding or removing operation and

there are M

i,v

distinct elements in S

, ordered as

i(1)

< c

i(2)

< ···< c

i(M

i,v

)

, where c

i(k)

is the k-th el-

ement with c

i(1)

= x

and c

i(M

i,v

)

= x

. Then the

mapping function z

) :[x

, x

]→[1, M

i,v

]takes the

following form:

) =k+

−c

i(k)

i(k+1)

−c

i(k)

, c

i(k)

≤ x

< c

i(k+1)

(11.20)

which maps c

i(k)

into the integer k. Thus, the transfor-

mation z(x) :Ω

→R

maps the center grid into a grid

with unit spacing between adjacent grid nodes such that

the radius of the RBF can be easily chosen. For the

raised-cosine RBF, the radius in every coordinate is se-

lected to be equal to one unit, that is, the radius will

touch but not extend beyond the neighboring grid nodes

in the uniform grid. This particular choice of the ra-

dius guarantees that for a given input x, the number of

nonzero raised-cosine RBFs in the uniform grid is at

most 2

To simplify the implementation, it is helpful to

reorder the M

grid nodes into a one-dimensional ar-

ray of points using a scalar index j. Let the vector

∈ R

be the index vector of the grid nodes, where

= (q

1,v

,...,q

n,v

)



with 1 ≤q

i,v

≤ M

i,v

. Then the

scalar index j can be uniquely determined by the index

vector q

, where

j =(q

n,v

−1)M

n−1,v

···M

2,v

1,v

+···

+(q

3,v

−1)M

2,v

1,v

+(q

2,v

−1)M

1,v

(11.21)

Let c

j,v

=(c

1j,v

,...,c

nj,v

)



denote the location of the

-th grid node in the original grid. Then the corre-

sponding grid node in the uniform grid is located at

j,v

= z(c

j,v

) =(q

1,v

,...,q

n,v

)



. Using the scalar in-

dex j in (11.21), the output

i,v

(x) ofthe self-organizing

raised-cosine RBF network implemented in the uniform

grid can be expressed as

(x) =



j=1

fj,v

j,v

(x)



j=1

fj,v

i=1





)−q

i,v





(11.22)

where the radius is one unit in each coordinate.

When implementing the output feedback controller,

the state vector estimate

x is used rather than the actual

state vector x. Itmay happen that

x /∈Ω

. In such a case,

the deﬁnition of the transformation (11.20) is extended

⎧

⎨

⎩

(

) =1if

< c

i(1)

(

) = M

i,v

> c

i(M

i,v

)

(11.23)

for i =1, 2,...,n.If

x ∈Ω

, the transformation(11.20)

is used. Therefore, it follows from (11.20)and(11.23)

that the function z(x) maps the whole n-dimensional

space

into the compact set [1, M

1,v

]×[1, M

2,v

]×

···×[1, M

n,v

11.3.5 Remarks

1. The internal structure of the self-organizing RBF

networkvaries as theoutput trackingerror trajectory

evolves. When the output tracking error is large, the

network adds RBFs in order to achieve better model

compensation so that the large output tracking error

Part B 11.3

Control of Uncertain Systems 11.4 State Feedback Controller Development 209

can be reduced. When, on the other hand, the output

tracking error is small, the network removes RBFs

in order to avoid a redundant structure. If the design

parameter e

max

is too large, the network may stop

adding RBFs prematurely or even never adjust its

structure at all. Thus, e

max

should be at least smaller

than |e(t

)|.However,ife

max

is too small, the net-

work may keep adding and removing RBFs all the

time and cannot approach a steady structure even

though the output tracking error is already within

the acceptable bound. In the worst case, the network

will try to add RBFs forever. This, of course, leads

to an unnecessary large network size and, at the

same time, undesirable high computational cost. An

appropriate e

max

may be chosen by trial and error

through numerical simulations.

2. The advantage of the raised-cosine RBF over the

Gaussian RBF is the property of the compact sup-

port associated with the raised-cosine RBF. The

number of terms in (11.22) grows rapidly with the

increase of both the number of grid nodes M

each coordinate and the dimensionality n of the in-

put space. For the GRBF network, all the terms

will be nonzero due to the unbounded support,

even though most of them are quite small. Thus,

a lot of computations are required for the net-

work’s output evaluation, which is impractical for

real-time applications, especially for higher-order

systems. However, for the RCRBF network, most

of the terms in (11.22) are zero and therefore do not

have to be evaluated. Speciﬁcally, for a given in-

put x, the number of nonzero raised-cosine RBFs

in each coordinate is either one or two. Conse-

quently, the number of nonzero terms in (11.22)

is at most 2

. This feature allows one to speed up

the output evaluation of the network in compari-

son with a direct computation of (11.22)forthe

GRBF network. To illustrate the above discussion,

suppose M

=10 and n = 4. Then the GRBF net-

work will require 10

function evaluations, whereas

the RCRBF network will only require 2

func-

tion evaluations, which is almost three orders of

magnitude less than that required by the GRBF

network. For a larger value of n and a ﬁner grid,

the saving of computations is even more dramatic.

The same saving is also achieved for the network’s

training. When the weights of the RCRBF net-

work are updated, there are also only 2

weights

to be updated for each output neuron, whereas

n × M weights has to be updated for the GRBF

network. Similar observations were also reported

in [11.60,p.6].

11.4 State Feedback Controller Development

The direct adaptive robust state feedback controller pre-

sented in this chapter has the form

u = u

a,v

s,v

(x)



−

(x)+y

(n)

−ke



s,v

, (11.24)

where

(x) =ω



f,v

(x),

(x) =ω



g,v

(x)andu

s,v

the robustifying component to be described later. To

proceed, let Ω

denote the compact set including all

the possible initial tracking errors and let

= max

e∈Ω



e , (11.25)

where P

is the positive-deﬁnite solution to the con-

tinuous Lyapunov matrix equation A



−2Q

for Q



> 0. Choose c

> c

and let



e :



e ≤c



(11.26)

Then the compact set Ω

is deﬁned as



x : x =e+x

, e ∈Ω

, x

∈Ω



over which the unknown functions f(x)andg(x) are

approximated.

For practical implementation, ω

f,v

and ω

g,v

are con-

strained, respectively, to resideinside compact sets Ω

f,v

and Ω

g,v

deﬁned as

f,v



f,v

:ω

≤ω

fj,v

≤ω

, 1 ≤ j ≤ M



(11.27)

and

g,v



g,v

:0<ω

≤ω

gj,v

≤ω

, 1 ≤ j ≤ M



(11.28)

where ω

, ω

and ω

are design parameters.

Let ω

∗

f,v

and ω

∗

g,v

denote the optimal constant weight

vectors corresponding to each admissible network

Part B 11.4

210 Part B Automation Theory and Scientiﬁc Foundations

structure, which are used only in the analytical analysis

and deﬁned, respectively, as

∗

f,v

= argmin

f,v

∈Ω

f,v

max

x∈Ω



f(x)−ω



f,v

(x)



(11.29)

and

∗

g,v

= argmin

g,v

∈Ω

g,v

max

x∈Ω



g(x)−ω



g,v

(x)



(11.30)

For the controller implementation, let

=max



max

x∈Ω



f(x)−ω

∗

f,v



(x)





(11.31)

and

=max



max

x∈Ω



g(x)−ω

∗

g,v



(x)





(11.32)

where max

(·) denotes the maximization taken over all

admissible structures of the self-organizing RBF net-

works. Let φ

f,v

=ω

f,v

−ω

∗

f,v

and φ

g,v

=ω

g,v

−ω

∗

g,v

and let

=max



max

f,v

,ω

∗

f,v

∈Ω

f,v

2η



f,v



(11.33)

and

=max



max

g,v

,ω

∗

g,v

∈Ω

g,v

2η



g,v



(11.34)

where η

and η

are positive design parameters of-

ten referred to as learning rates. It is obvious that

(or c

) will decrease as η

(or η

) increases. Let

σ = b



e. The following weight vector adaptation

laws are employed, respectively, for the weight vectors

and ω

f,v

=Proj



f,v

,η

σξ

(x)



(11.35)

and

g,v

=Proj



g,v

,η

σξ

(x)u

a,v



(11.36)

where Proj(ω

, θ

) denotes Proj(ω

j,v

, θ

j,v

)forj =

1,...,M

and

Proj(ω

j,v

, θ

j,v

) =

⎧

⎪

⎨

⎪

⎩

0ifω

j,v

=ω and θ

j,v

< 0 ,

0ifω

j,v

=ω and θ

j,v

> 0 ,

j,v

otherwise ,

(11.37)

is a discontinuous projection operator proposed

in [11.65]. The robustifying component u

s,v

is designed

s,v

=−

s,v

sat





(11.38)

where k

s,v

a,v

|+d

and sat(·) is the satura-

tion function with small ν>0. Let

max



max|u

a,v



, (11.39)

where theinner maximizationis taken over e ∈Ω

, x

∈

, y

(n)

∈Ω

, ω

f,v

∈Ω

f,v

,andω

g,v

∈Ω

g,v

It can be shown [11.58] that, for the plant (11.2)

driven by the proposed direct adaptive robust state feed-

back controller (DARSFC)(11.24) with the robustify-

ing component (11.38) and the adaptation laws (11.35)

and (11.36), if one of the following conditions is

satisﬁed:

•

The dwelling time T

of the self-organizing RBF

network is selected such that

≥





(11.40)

•

The constants c

, c

,andν satisfy the inequality

0 < c

exp(μT

)−1

3−2exp(μT

)

4μ

(11.41)

where μ is the ratio of the minimal eigenvalve of Q

to the maximal eigenvalue of P

.Ifη

, η

,andν are

selected such that

≥max



, 2



8μ





(11.42)

then e(t) ∈Ω

and x(t) ∈Ω

for t ≥t

. Moreover, there

exists a ﬁnite time T ≥t

such that



(t)P

e(t) ≤2



8μ



(11.43)

for t ≥T. If, in addition,there exists aﬁnite time T

≥t

such that v =v

for t ≥ T

, then there exists a ﬁnite time

T ≥ T

such that



(t)P

e(t) ≤2



8μ



(11.44)

for t ≥ T. It can be seen from (11.43)and(11.44)that

the tracking performance is inversely proportional to η

Part B 11.4

Control of Uncertain Systems 11.5 Output Feedback Controller Construction 211

and η

, and proportional to ν. Therefore, larger learn-

ing rates and smaller saturation boundary imply better

tracking performance.

11.4.1 Remarks

1. For the above direct adaptive robust controller, the

weight vector adaptation laws are synthesized to-

gether with the controller design. This is done for

the purpose of reducing the output tracking error

only. However, the adaptation laws are limited to

be of gradient type with ceratin tracking errors as

driving signals, which may not have as good con-

vergence properties as other types of adaptation

laws such as the ones based on the least-squares

method [11.66]. Although this design methodology

can achieve excellent output tracking performance,

it may not achieve the convergence of the weight

vectors. When good convergence of the weight vec-

tors is a secondary goal to be achieved, an indirect

adaptive robust controller [11.66] or an integrated

direct/indirect adaptive robust control [11.65]have

been proposed to overcome the problem of poor

convergence associated with the direct adaptive ro-

bust controllers.

2. It seems to be desirable to select large learning rates

and small saturation boundary based on (11.43)

and (11.44). However, it is not desirable in prac-

tice to choose excessively large η

and η

.Ifη

and η

are too large, fast adaptation could excite

the unmodeled high-frequency dynamics that are

neglected in the modeling. On the other hand, the

selection of ν cannot be too small either. Otherwise,

the robustifying component exhibits high-frequency

chattering, which may also excite the unmodeled

dynamics. Moreover, smaller ν requires higher

bandwidth to implement the controller for small

tracking error. To see this more clearly, consider the

following ﬁrst-order dynamics,

e =ae+



f +gu −



, (11.45)

which is a special case of (11.6). Applying the fol-

lowing controller,

u =



−

f +

−ke



−

sat





(11.46)

where σ = e, one obtains

e =−a

d −

sat





(11.47)

where −a

= a−k < 0. When |e|≤ν,(11.47)

becomes

e =−





d ,

(11.48)

which implies that smaller ν results in higher con-

troller bandwidth.

11.5 Output Feedback Controller Construction

The direct adaptive robust state feedback controller pre-

sented in the previous section requires the availability

of the plant states. However, often in practice only the

plant outputs are available. Thus, it is desirable to de-

velopa directadaptive robust output feedbackcontroller

(DAROFC) architecture. To overcome the problem of

inaccessibility of the system states, the following high-

gain observer [11.38,49],

e =A

e+l



e−c



(11.49)

is applied to estimate the tracking error e. The observer

gain l is chosen as

l =



,...,





, (11.50)

where ∈ (0, 1) is a design parameter and α

, i = 1, 2,

...,n, are selected so that the roots of the poly-

nomial equation, s

+α

n−1

+···+α

n−1

s+α

= 0,

have negative real parts. The structure of the above

high-gain tracking error observer is shown in Fig. 11.8.

Substituting e with

e in the controller u deﬁned in

(11.24) with (11.38)gives

u =

a,v

s,v

, (11.51)

where

a,v

(



−

(

x)+y

(n)

−k



(11.52)

and

s,v

=−

s,v

sat





(11.53)

with

x = x

s,v

= d

a,v

|+d

and

σ =



e.Let

max



max|

a,v



Part B 11.5

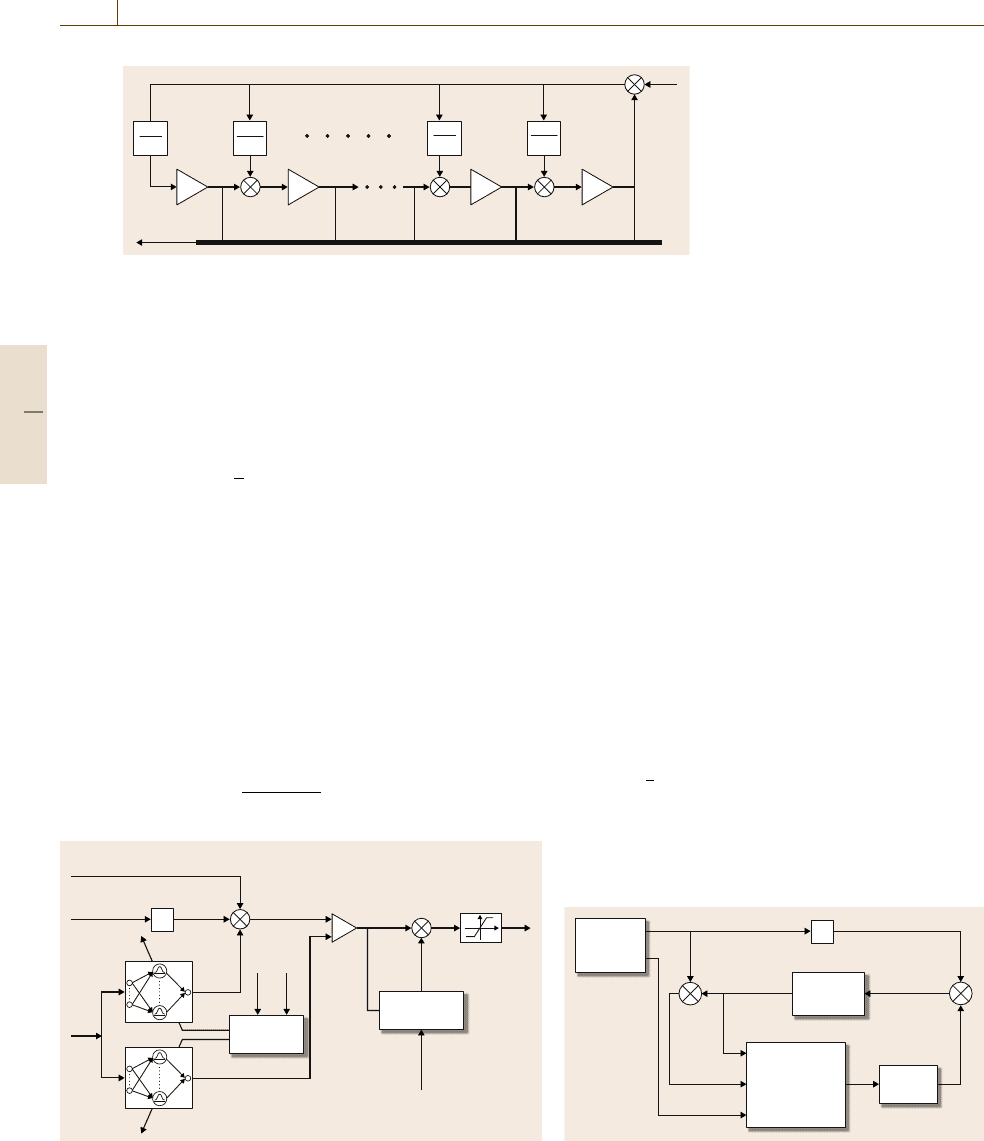
212 Part B Automation Theory and Scientiﬁc Foundations

(n–1)

n–1

∫

(n–2)

∫

(1)

(2)

∫

–

Fig. 11.8 Diagram of the high-gain

observer

and the inner maximization is taken over

e ∈ Ω

∈Ω

, y

(n)

∈Ω

, ω

f,v

∈Ω

f,v

,andω

g,v

∈Ω

g,v

.For

the high-gain observer described by (11.49), there exist

peaking phenomena [11.67]. Hence, the controller

u de-

ﬁned in (11.51) cannot be applied to the plant directly.

To eliminate the peaking phenomena, the saturation is

introduced into the control input

u in (11.51). Let



e :



e ≤c



(11.54)

where c

> c

.Let

S ≥max



max





e, x

, y

(n)

, ω

f,v

, ω

g,v







(11.55)

where u is deﬁned in (11.24) and the inner maxi-

mization is taken over e ∈Ω

, x

∈ Ω

, y

(n)

∈ Ω

f,v

∈ Ω

f,v

,andω

g,v

∈ Ω

g,v

. Then the proposed di-

rect adaptive robust output feedback controller takes the

form

= S sat



a,v

s,v



(11.56)

Adaptation

algorithms

Robustifying

component

(n)

–

Fig. 11.9 Diagram of the direct adaptive robust output feedback

controller (DAROFC)

The adaptation laws for the weight vectors ω

f,v

and

g,v

change correspondingly and take the following

new form, respectively

f,v

=Proj



f,v

,η

σξ

(



(11.57)

and

g,v

=Proj



g,v

,η

σξ

(

a,v



(11.58)

A block diagram of the above direct adaptive robust

output feedback controller is shown in Fig.11.9, while

a block diagram of the closed-loop system is given

in Fig.11.10.

For the high-gain tracking error observer (11.49),

it is shown in [11.68] that there exists a con-

stant

∗

∈ (0, 1) such that, if ∈ (0,

∗

), then e(t)−

e(t)≤β with β>0fort ∈[t

( ), t

), where

( ) is a ﬁnite time and t

is the moment when

the tracking error e(t) leaves the compact set Ω

for

the ﬁrst time. Moreover, we have lim

→0

( ) = 0

and c

e(t

( ))



e(t

( )) < c

.Forthe

plant (11.2) driven by the direct adaptive robust output

feedback controller given by (11.56) with the adapta-

tion laws (11.57)and(11.58), if one of the following

conditions is satisﬁed:

Self-organizing

RCRBF

Network-based

DAROFC

Plant

High-gain

observer

Reference

signal

generator

(n)

–

Fig. 11.10 Diagram of the closed-loop system driven by the

output feedback controller

Part B 11.5

Control of Uncertain Systems 11.6 Examples 213

•

The dwelling time T

of the self-organizing RBF

network is selected such that

≥





(11.59)

•

The constants c and ν satisfy the inequality

0 < c

exp(μT

)−1

3−2exp(μT

)



4μ



(11.60)

and if η

, η

,andν are selected such that

≥c

(11.61)

and

> 2



8μ



, (11.62)

there exists a constant

∗

∈(0, 1) suchthat, if ∈(0,

∗

then e(t) ∈Ω

and x(t) ∈Ω

for t ≥t

. Moreover, there

exists a ﬁnite time T ≥t

( ) such that

e(t)



e(t) ≤2



8μ



+r +c

(11.63)

with some r > 0fort ≥ T. In addition, suppose that

there exists a ﬁnite time T

≥t

( ) such that v =v

for t ≥ T

. Then there exists a ﬁnite time T ≥ T

such

that



(t)P

e(t) ≤2



8μ



(11.64)

for t ≥ T. A proof of the above statement can be found

in [11.58]. It can be seen that the performance of the

output feedback controller approaches that of the state

feedback controller as approaches zero.

11.6 Examples

In this section, two example systems are used to il-

lustrate the features of the proposed direct adaptive

robust controllers. In Example 11.1, a benchmark prob-

lem from the literature is used to illustrate the controller

performance under different situations. Especially, the

reference signal changes during the operation in or-

der to demonstrate the advantage of the self-organizing

0 5 10 15 20

Time (s)

2.5

1.5

0.5

–0.5

–1

–1.5

–2

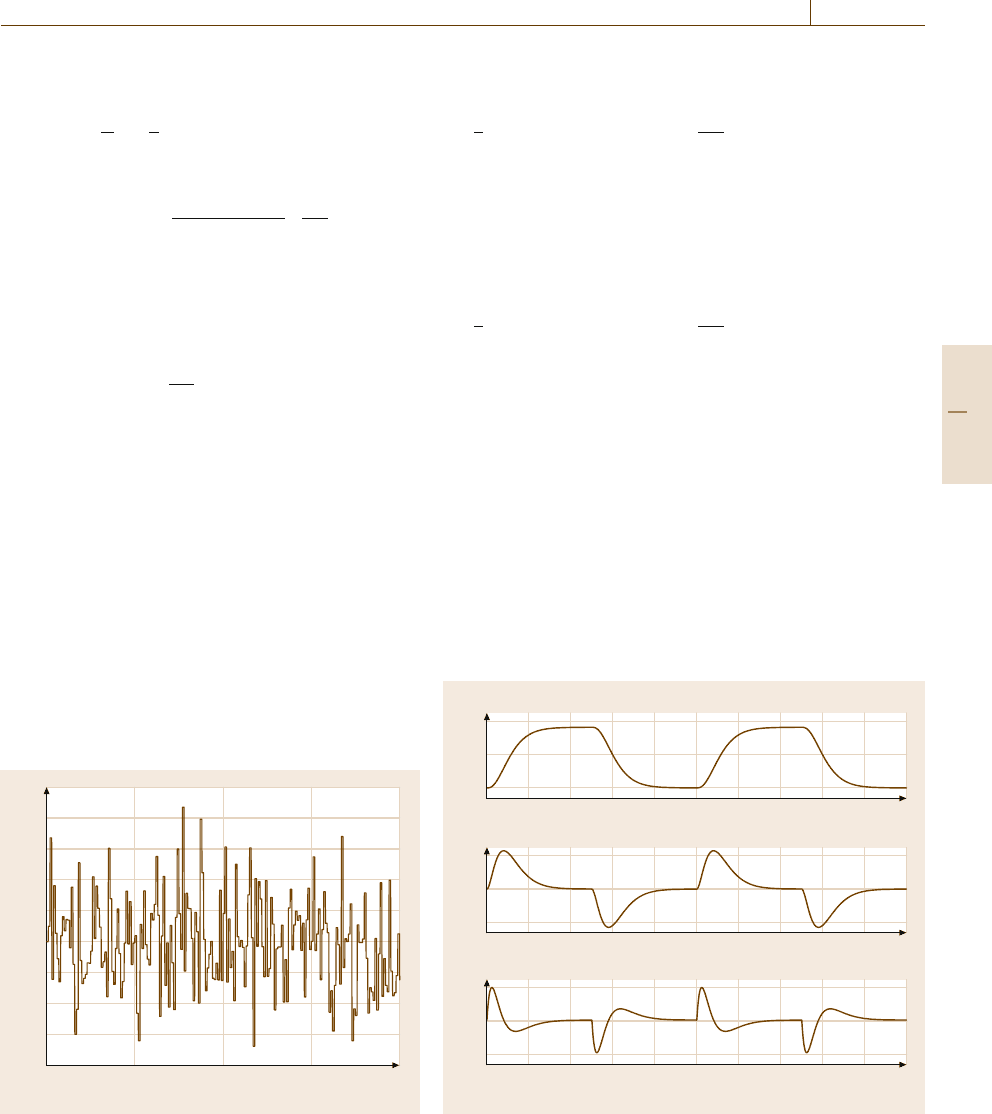
Fig. 11.11 Disturbance d in example 11.1

RBF network. In Example 11.2, the Dufﬁng forced

oscillation system is employed to test the controller per-

formance for time-varying systems.

0.5

0.5 1 1.5 2 2.5

Reference signal

First time derivative

Second time derivative

3 3.5 4 4.5

–2

0.5 1 1.5 2 2.5 3 3.5 4 4.5

Time (s)

–20

0.5 1 1.5 2 2.5 3 3.5 4 4.5

Fig. 11.12 Reference signal and its time derivatives

Part B 11.6

214 Part B Automation Theory and Scientiﬁc Foundations

Time (s)

Number of hidden neurons

5101520

0 25

Control input

–10

–20

5101520

0 25

Tracking error

× 10

–3

a) DARSFC

–5

5101520

Time (s)

Number of hidden neurons

5101520

0 25

Control input

–10

–20

5101520

0 25

Tracking error

× 10

–3

b) DAROFC

–5

5101520

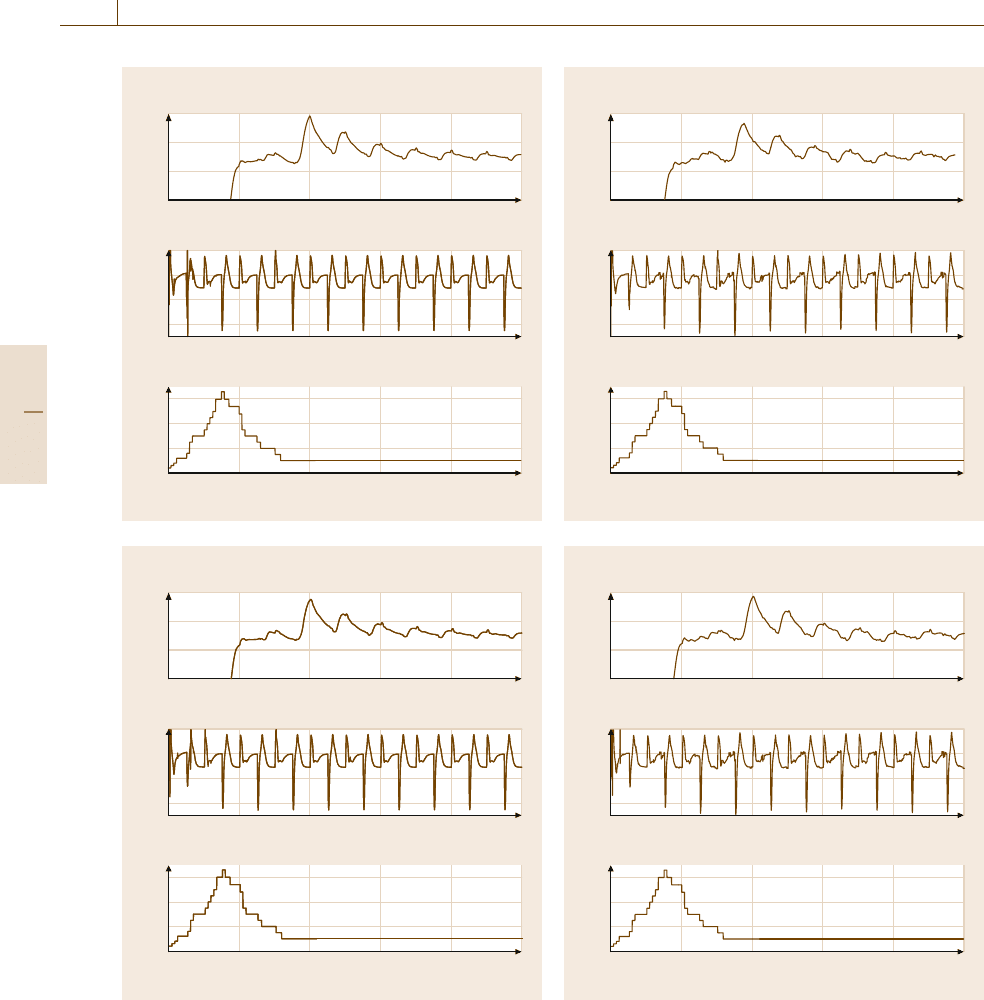
Fig. 11.13a,b Controller performance without disturbance

in example 11.1.

(a) State feedback controller, (b) output

feedback controller

Time (s)

Number of hidden neurons

5 101520

0 25

Control input

–10

–20

5 101520

0 25

Tracking error

× 10

–3

a) DARSFC

–5

5 101520

Time (s)

Number of hidden neurons

5 101520

0 25

Control input

–10

–20

5 101520

0 25

Tracking error

× 10

–3

b) DAROFC

–5

5 101520

Fig. 11.14a,b Controller performance with disturbance in

Example 11.1.

(a) State feedback controller, (b) output

feedback controller

Part B 11.6