Никифорова И.А. Математика в экономике: сборник задач. Часть ?
Подождите немного. Документ загружается.

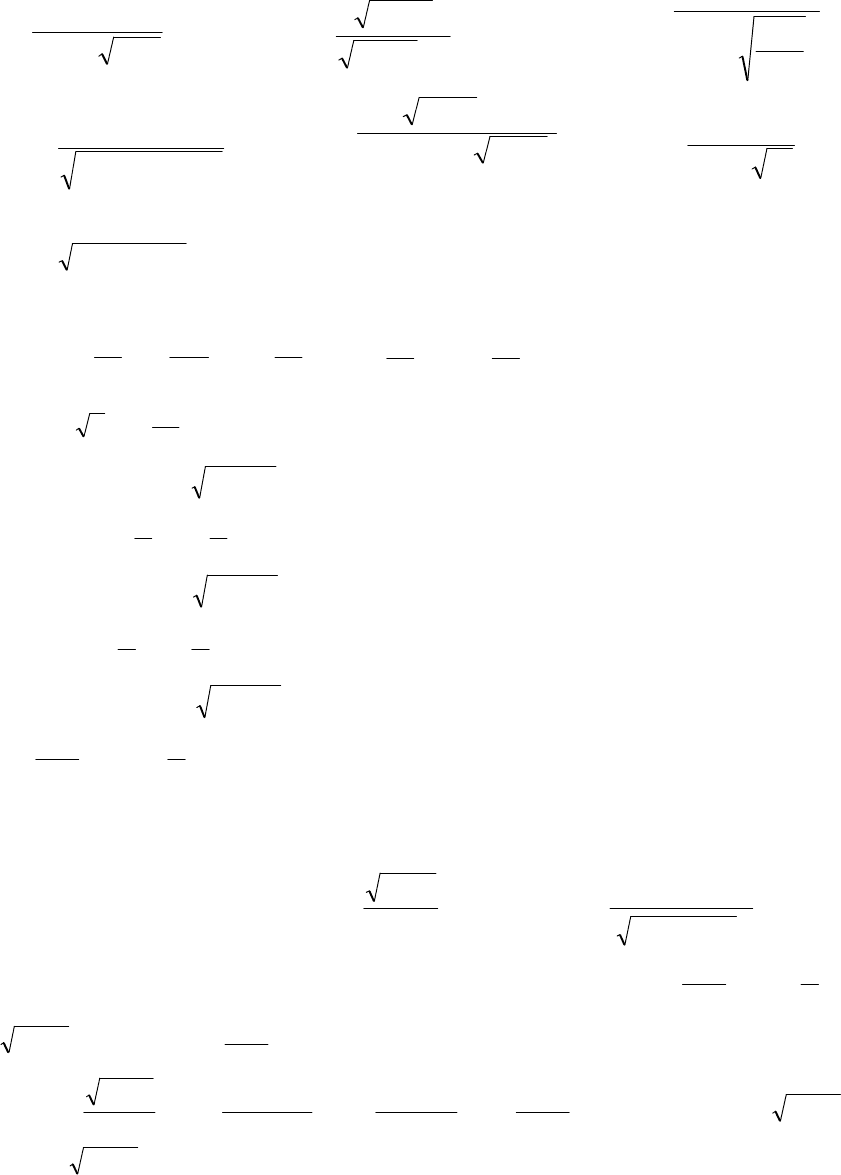
131
7)
( )
∫
++ xx
dx
15
;
8)
∫
+−
−
dx
x
x
1
3
2
32
3
;
9)
∫
−
+
3
1
2
x
x
x
dx
;
10)
( )( )
∫
−+
3
42
11 xx
dx
;
11)
( )
(
)
∫
+++
−+
dx
axax
ax
3
6
1
1
,
−
a
параметр;
12)
( )
∫
−
4 3
1 xx
dx
.
2. Тригонометрические подстановки. Интегралы вида
(
)
Rx ax bx cdx,
2
+ +
∫
можно сначала преобразовать, выделив полный квадрат из
квадратного трёхчлена:
ax
bx
c
2
+
+
=
=−+
+⋅⋅+
a
b
c
a
b
x
a
b
xa
4
4
2
2
2
2
2
2
a
b
c
a
b
xa
42
2
2
−+
+
, а затем при помощи подста-
новки
ax
b
a
u+
=
2
свести к одному из интегралов:
1)
(
)
−−
∫
duupuR
22
,
интегрируется при помощи подстановки
u p t t= − < <sin,
π
π
2
2
;
2)
(
)
Ru p u du,
2 2
+ −
∫
интегрируется при помощи подстановки
u ptgt t= − < <,
π
π
2
2
;
3)
(
)
Ru u p du,
2 2
− −
∫
интегрируется с помощью подстановки
u
p
t
t= < <
cos
,0
2
π
.
В результате интегралы 1) - 3) приводятся к интегралам ви-
да
( )
R t tdtsin,cos
∫
.
Пример 4.14. Найти: 1)
∫
>
−
0,
1
2
xdx
x
x
; 2)
(
)
∫
++
3
2
25 xx
dx
.
Решение. 1) Здесь интеграл типа 3). Положим
2
0,
cos
1
π
<<= t
t
x
, тогда
x tgt
2
1− =
,
dx tgt
dt
t
=
cos
. Подставляя в интеграл, получим
x
x
dx
tgt t
t
dt
t
t
dt
dt
t
dt
2 2 2
2 2
1 1−
=
⋅
=
−
= − =
∫∫∫ ∫∫
cos
cos
cos
cos
cos
tgt t C x−+ = −
2
1
− −+arctg x С
2
1
.
2) Выделим полный квадрат в трёхчлене, получим
(
)
5 2 1 4
2
2
+ + = + +x x x
. Пропуская промежуточную переменную, сделаем под-
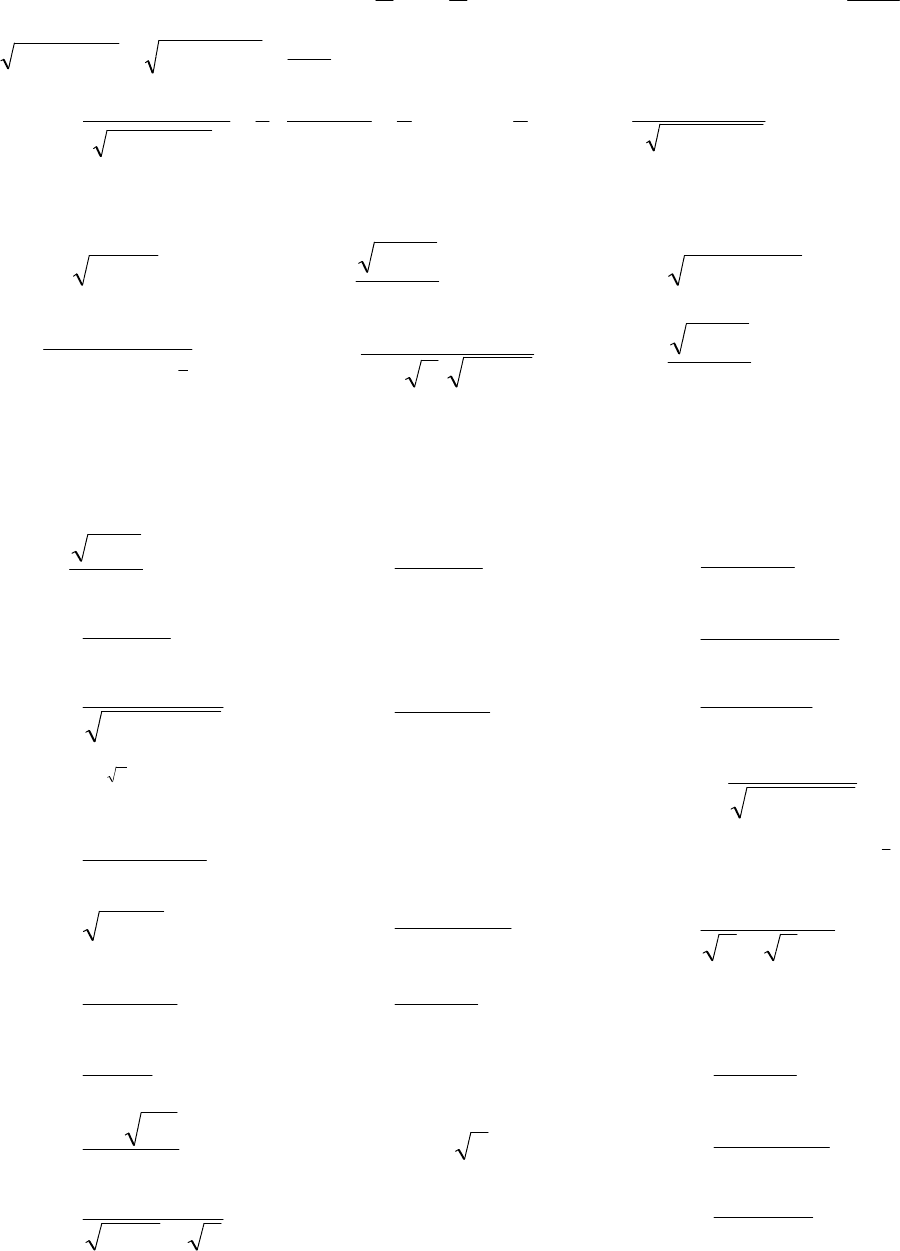
132
становку
x tgt t+ = − < <1 2
2
2
,
π
π
, тогда
dx
dt
t
=
2
2
cos
,
( )
5 2 1 4
2
2
2
+ + = + + =x x x
t
cos
. Осуществляя подстановку, найдём
( )
dx
x x
tdt
t
tdt
5 2
1
4
1
4
2
3
3
2
+ +
=
⋅
= =
∫ ∫ ∫
cos
cos
cos
1
4
1
45 2
2
sint C
x
x x
C+ =
+
+ +
+ .
4.98. Найти интегралы при помощи тригонометрических подстановок:
1)
∫
− dxxx
22
4 ;
2) dx
x
x
∫
+
2
1
;
3)
∫
−− dxxx
2
21 ;
4)
( )
∫
+−
2
3
2
52xx
dx
;
5)*
( )
∫
−+
2
1 xxx
dx
;
6) dx
x
x
∫
−
2
2
1
;
4.7. Смешанные примеры на интегрирование
Найти интегралы.
4.99.
dx
x
x
∫
+1
.
4.100. dx
x
xarctg
∫
+
1
2
2
.
4.101.
∫
+
23
ax
x
dx
.
4.102.
∫
+
x
dx
sin
1
.
4.103.
∫
⋅ xdxtgx
2
.
4.104.
∫
−
+
5
4
2 xx
x
e
e
dxe
.
4.105.
(
)
∫
+−
−
16
3
2
xx
dxx
.
4.106.
∫
x
xdx
sin
cos
2
.
4.107.
(
)
( )
∫
+
−
4
bax
dxbax
.
4.108.
∫
−
dxe
x
4.109.
(
)
∫
+ dxxx
2
ln
.
4.110.*
(
)
∫
−−
+
2
2
4
xx
dxx
.
4.111.
dx
x
x
x
∫
+
+
+
4
2
3
2
.
4.112.
dxxx
∫
⋅ 3sin2sin
.
4.113.
( )
∫
−
⋅+− dxexx
x
2
2
122
.
4.114.
∫
− dx
x
12
.
4.115.
( )
∫
−
dx
x
x
4
sin1
cos
.
4.116.
∫
+− 1
4
xx
dx
.
4.117.
(
)
∫
dx
x
x
2
sin
cosln
. 4.118.
∫
+
24
x
x
dx
.
4.119.
(
)
(
)
∫
+++ dxxxx 14cos2
2
.
4.120.
∫
+
−
arctgxdx
x
x
1
2
2
2
.
4.121.
∫
⋅ xdxx 3sinsin
2
.
4.122.
∫
+
−
dx
x
xx
3
23
.
4.123.
∫
−
dx
x
tgx
2
3
cos
2
.
4.124.
∫
dxxarctg .
4.125.
∫
−
+
+
dx
e
e
ee
xx
xx
2
23
2
2
.
4.126.
∫
++ xax
dx
.
4.127.
∫
xdx2lncos
.
4.128.
( )
∫
+
−
dx
x
x
4
32
32
.
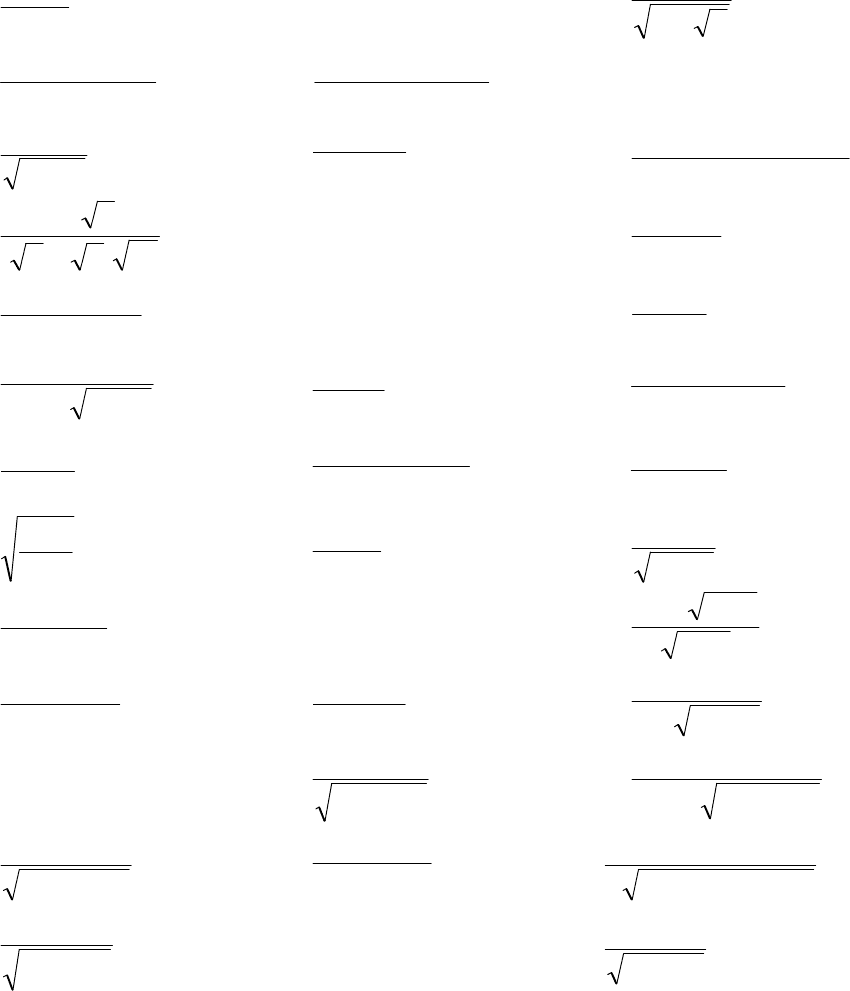
133
4.129.
∫
dx
x
x
4
3
sin
cos
.
4.130.
(
)
∫
− dxx
2
ln1 .
4.131.
∫
+ xx
dx
.
4.132.
∫
−+−
+
dx
x
x
x
x
1
1
23
4
.
4.133.
∫
+
x
x
dx
22
cos
sin
9
.
4.134.
∫
xdxx
2
cos
.
4.135.
∫
+
dx
x
x
1
2
3
.
4.136.
( )
∫
+
2
2
1 x
dx
.
4.137.
∫
+
x
b
x
a
dx
2222
sin
cos
.
4.138.
(
)
∫
−
−
dx
xxx
x
4 3
43
6
1
.
4.139.
∫
xdxx
2
ln .
4.140.
∫
+ tgx
dx
34
.
4.141.
∫
−
−
−−
dx
e
e
ee
xx
xx
3
2
32
2
2
.
4.142.
(
)
∫
− xdxx 2cos12
2
.
4.143.
∫
dx
x
xx
3
sin
cos
.
4.144.
( )
∫
−+
2
11 xx
dx
.
4.145.
∫
+
dx
x
tgx
2
sin
1
.
4.146.
( )( )
∫
+− 32
2
xx
dx
.
4.147.
∫
dx
x
arctgx
2
.
4.148.
( )
∫
−
++
⋅
2
2
2
xx
x
ee
dxe
.
4.149.
∫
+
x
dx
cos
2
.
4.150.
∫
+
−
dx
x
x
1
1
.
4.151.
∫
dx
x
x
3
cos
2sin
.
4.152.
∫
+
dx
e
xe
x
x
1
.
4.153.
∫
−
−
dx
x
x
x
1
2
3
.
4.154.
∫
⋅ dxee
xx
sin
2
.
4.155.
∫
+
++
dx
x
xx
3
2
1
1
.
4.156.
∫
−
x
dx
2
sin
4
3
. 4.157.
∫
+
x
xdx
cos
1
.
4.158.
∫
−+
dx
x
x
2
3
42
.
4.159.
∫
⋅ xdxx cosln2sin
.
4.160.
( )
∫
+
dx
x
x
5
2
14
. 4.161.
∫
+ xtgx
dx
22
52cos
.
4.162.
∫
++ 2
2
xx
xdx
.
4.163.
( )
∫
+
2
45
1xx
dx
.
4.164.
∫
−+ xxx
xdx
2
lnln46
ln
.
4.165.
( )
∫
−
3
2
4
1 x
dxx
.
4.166.
∫
xdxxarcsin
.
4.167.
∫
+
dx
x
x
16
4
.
134
Глава 5 ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
5.1. Понятие определённого интеграла. Основные свойства
1. Понятие определённого интеграла. Пусть функция
(
)
xf
определена
на отрезке
[
]
ba,
. Разделим отрезок
[
]
ba,
произвольным образом на
n
частей
точками
....
210
bxxxax
n
=
<
<
<
<
=
На каждом из получившихся отрезков
[
]
ii
xx ,
1−
длины
1−
−
=
∆
iii
xx
выберем произвольную точку
ξ
i
∈
[
]
ii
xx ,
1−
,
n
i
...,
,
1
=
. Построим для функции
(
)
xf
на отрезке
[
]
ba,
интегральную сумму
(
)
i
n
i
i
f ∆⋅=
∑
=1
ξσ
и положим
i
ni
∆
=
= ,...,1
max
λ
.
Если существует предел интегральных сумм при
0
→
λ
, не зависящий
от способа разбиения отрезка
[
]
ba,
и выбора точек
i
ξ
, то этот предел назы-
вают определённым интегралом от функции
(
)
xf
на отрезке
[
]
ba,
и обозна-
чают символом
()
∫
b
a
dxxf
:
()
0
lim
→
=
∫
λ
b
a
dxxf
(
)
i
n
i
i
f ∆⋅
∑
=1
ξ
,
функцию
(
)
xf
в этом случае называют интегрируемой на отрезке
[
]
ba,
.
•
Если функция непрерывна на от-
резке
[
]
ba,
, то она интегрируема на этом
отрезке.
•
Если функция интегрируема на
отрезке
[
]
ba,
, то она ограничена на этом
отрезке.
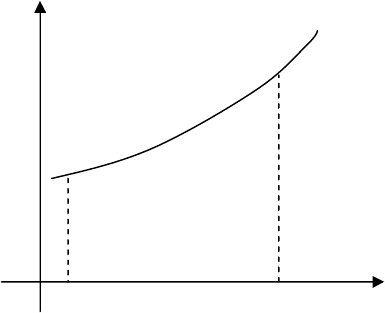
•
Геометрический смысл опреде-
лённого интеграла. Пусть функция
(
)
xf
непрерывна на отрезке
[
]
ba,
. Если
(
)
[
]
baxxf ,0
∈
∀
≥
, то
()
∫
b
a
dxxf
численно
равен площади криволинейной трапе-
ции, ограниченной прямыми
,
a
x
=
,bx
=
осью
Ox
и кривой
(
)
xfy
=
, см. рис.
5.1.
Пример 5.1. Вычислить интеграл
∫
1
0
2
dxx
как предел интегральной сум-
мы.
0 a b x
y = f(x)
Рис.5.1.
y
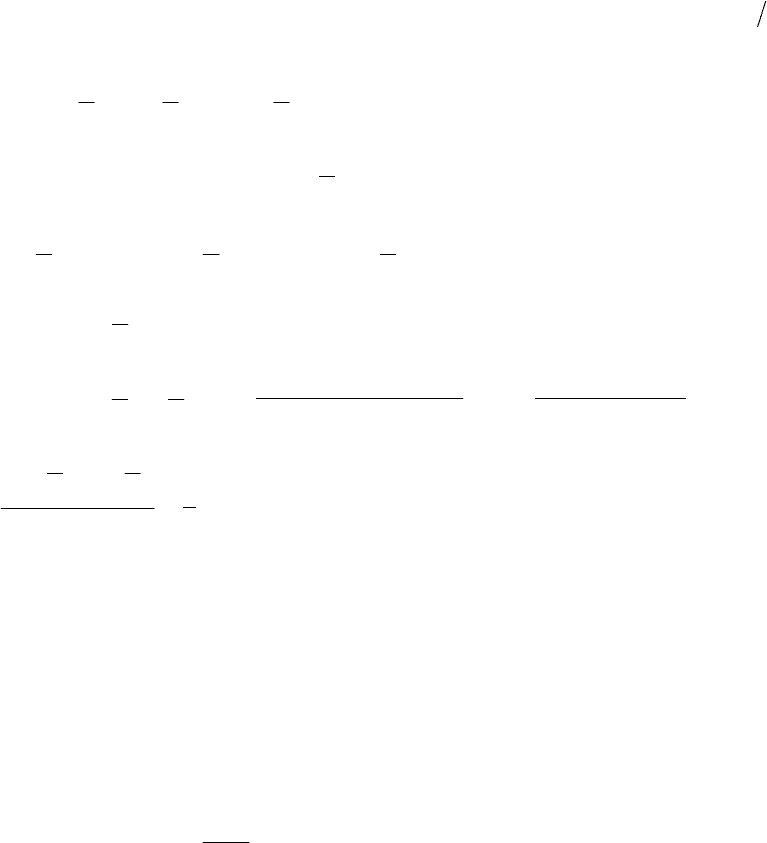
135
Решение. Функция
(
)
2
xxf =
непрерывна на отрезке
[
]
1,0
, следователь-
но, интегрируема на этом отрезке. Построим интегральную сумму следую-
щим образом. Разделим отрезок
[
]
1,0
на
n
равных частей, тогда
n
i
1
=
∆
n
i
,...,
1
=
∀
и
,0
0
=
x
,
1
1
n
x = ,...,
2
2
n
x = .1==
n
n
x
n
Выберем
ii
x
=
ξ
, тогда
( )
2
=
n
i
f
i
ξ
n
i
,...,
1
=
∀
, т.е.
( )
,
1
2
1
=
n
f ξ
( )
,...,
2
2
2
=
n
f ξ
( )
2
=
n
n
f
n
ξ
.
Очевидно,
n
1
=λ и
∞
→
⇔
→
n
0
λ
. Следовательно,
=⋅
=
∑
∫
=
∞→
nn
i
dxx
n
i
n
1
lim
2
1
1
0
2
=
++++
∞→
3
2222
...321
lim
n
n
n
(
)
(
)
=
+
+
∞→
3
6
121
lim
n
nnn
n
= =
+
+
∞→
6
1
2
1
1
lim
nn
n
1
3
.
Здесь использована формула суммы квадратов натуральных чисел
(см.пр.1.23. 2)).
5.1. Рассмотреть задачи, приводящие к понятию определённого инте-
грала:
1) о нахождении объёма продукции
Q
, произведённой за промежуток
времени
[
]
T;0
, если известна функция
(
)
tuu
=
, описывающая изменение
производительности труда на предприятии с течением времени: а) в общем
виде; б)* если
8
=
T
ч,
()
1
4
+
=
t
tu (ед./ч);
2) о нахождении прироста капитала (основных фондов)
K
∆
за период с
момента времени
1
t
до
2
t
по известным чистым инвестициям
(
)
tI
: а) в об-
щем виде; б) при
1
1
=
t
,
3
2
=
t
,
(
)
12
−
=
ttI
(млн. руб./год).
5.2. Пусть известна функция
(
)
qMC
, описывающая зависимость пре-
дельных издержек
MC
от объёма произведённой продукции
q
. Выписать
формулы для вычисления: 1) прироста суммарных издержек и 2) среднего
прироста (иначе, средней скорости изменения) суммарных издержек при про-
изводстве продукции в пределах от
1
q
до
2
q
единиц.

136
5.3. С помощью предельного перехода от интегральных сумм вычис-
лить
∫
4
1
3
dxx
, разбивая отрезок
[
]
4;1
: 1) на равные части; 2) точками, образую-
щими геометрическую прогрессию.
В каждом из указанных разбиений в качестве
i
ξ
выбирать: а) левые
концы отрезков; б) правые концы отрезков; в) середины отрезков
[
]
ii
xx ,
1−
.
5.4. Вычислить определённые интегралы, рассматривая их как преде-
лы соответствующих интегральных сумм:
1)
( )
∫
+
4
0
1 dxx ; 2)
∫
2
1
2
1
* dx
x
.
5.5. Численность населения N в любой момент времени t (г) задаётся
функцией
(
)
tfN
=
. Потребление некоторого продукта пропорционально чис-
ленности населения с коэффициентом пропорциональности k. Считая
(
)
tf
непрерывной функцией, записать формулу для подсчёта объёма потребления
рассматриваемого продукта за первое полугодие второго года с момента на-
чала отсчёта.
5.6. Функция
(
)
xf
описывает плотность движения грузов в любой
точке железной дороги, находящейся на расстоянии x (км) от выбранного на-
чала железной дороги. Указанная плотность движения грузов измеряется ве-
сом в тоннах всех грузов, проходящих за год через эту точку. Написать фор-
мулу для подсчёта годового объёма перевозок по железной дороге от её нача-
ла до L−го км, предполагая
(
)
xf
непрерывной на отрезке
[
]
L;0 .
2. Основные свойства определённого интеграла
1. Если
(
)
xf
интегрируема на
[
]
ba,
,
−
k
произвольное число, то
(
)
xfk
⋅
интегрируема на
[
]
ba, и
() ()
∫∫
⋅=⋅
b
a
b
a
dxxfkdxxfk
.
2. Если
(
)
xf
и
(
)
xg
интегрируемы на
[
]
ba,
, то
(
)
±
xf
(
)
xg
интегрируе-
мы на
[
]
ba,
и
() ()( ) () ()
dxxgdxxfdxxgxf
b
a
b
a
b
a
⋅±⋅=⋅±
∫∫∫
.
3.
()
0=⋅
∫
dxxf
a
a
. 4.
() ()
∫∫
⋅−=⋅
a
b
b
a
dxxfdxxf
. 5.
() () ()
∫∫∫
+=
b
c
c
a
b
a
dxxfdxxfdxxf
6. Если
(
)
∈
∀
≥
xxf 0
[
]
ba,
, то
()
0≥⋅
∫
dxxf
b
a
.

137
7. Если
(
)
(
)
∈
∀
≥
xxgxf
[
]
ba,
, то
()
≥⋅
∫
dxxf
b
a
()
dxxg
b
a
⋅
∫
.
8. Если
(
)
(
)
∈
∀
≥
xxgxf
[
]
ba,
и существует точка
[
]
bax ,
0
∈
, в которой
(
)
(
)
00
xgxf
>
, причём обе функции
f
и
g
непрерывны в этой точке, то
()
>
∫
dxxf
b
a
()
gxdx
a
b
∫
.
Свойства 4-8 формулируются в предположении, что все используемые в
них интегралы существуют.
9. Если
(
)
fxнепрерывна на
[
]
ba, ,
−
m
наименьшее,
−
M
наибольшее
значение
(
)
xf на
[
]
ba, , то
( ) () ( )
abMdxxfabm
b
a
−⋅≤⋅≤−⋅
∫
.
10. (Теорема о среднем.) Если
(
)
xf
непрерывна на
[
]
ba,
, то существует
точка
[
]
bac ,
∈
такая, что справедливо равенство:
() ()( )
abcfdxxf
b
a
−=
∫
,
при этом
(
)
cf
называют средним значением функции на отрезке
[
]
ba,
.
5.7. Исходя из геометрического смысла и свойств определённого ин-
теграла, доказать, что:
1)
∫
=
π2
0
02sin xdx
; 2)
( )
∫
=+
2
1
412 dxx
; 3)
∫
−
=−
3
3
2
2
9
9
π
dxx
.
5.8. Выяснить (не вычисляя), какой из интегралов больше:
1)
∫
1
0
2
dxe
x
или
∫
1
0
dxe
x
;
2)
∫
2
1
2
dxe
x
или
∫
2
1
dxe
x
;
3)
∫
−
+
1
1
4
1 dxx
или
∫
−
1
1
2
dxx
; 4)
∫
1
0
23
cos xdxx
или
∫
1
0
22
cos xdxx
;
5)
∫
e
xdxx
0
ln
или
∫
e
xdxx
0
2
ln
;
6)
∫
2
0
sin
π
xdx
n
или
∫
+
2
0
1
sin
π
xdx
n
;
7)
∫
−
−
1
2
3
1
dx
x
или
∫
−
−
1
2
3 dx
x
.

138
5.9. Доказать неравенства
1)
∫
<
+
<
2
0
5
1
106
1
x
dx
;
2)
∫
<<
1
0
2
1 edxe
x
; 3)
∫
<
+
<
2
1
2
2
1
15
2
x
xdx
;
4)
∫
<
+
+
<
18
8
5,9
2
1
9 dx
x
x
; 5)
∫
<
+
<
1
0
3
8
7
8
1
1
0
x
dxx
.
5.10. Оценить интегралы:
1)
∫
+
=
π2
0
cos210 x
dx
J
;
2) dx
x
x
J
∫
=
2
6
2
cos
π
π
;
3)
∫
+=
2
0
4
9 dxxJ
;
4)
∫
+
+
=
2
0
2
2
3
2
dx
x
x
J ;
5) dx
x
ctgx
J
∫
=
2
4
π
π
.
5.2. Вычисление определённого интеграла
1. Формула Ньютона-Лейбница. Если функция
(
)
xf
непрерывна на
отрезке
[
]
ba, и
(
)
−
xF её первообразная, то верна формула Ньютона-
Лейбница
() () ()
=−=
∫
aFbFdxxf
b
a
(
)
b
a
xF |
Пример. 5.2. Вычислить
( )
∫
−
e
xx
dx
1
2
ln1
.
Решение.
( )
=
−
∫
e
xx
dx
1
2
ln1
(
)
( )
=
−
∫
e
x
xd
1
2
ln1
ln
(
)
=
e
x
1
|lnarcsin
(
)
−elnarcsin
(
)
=
1lnarcsin
−
2
1
arcsin
6
0arcsin
π
= .
5.11. Используя формулу Ньютона-Лейбница, вычислить интегралы:
1)
( )
dxxx
∫
+−
2
1
2
123
;
2)
(
)
dxxx
∫
+
1
0
3
2
; 3)
dx
x
∫
3
0
2
;
4)
∫
−
2
1
12x
dx
;
5)
∫
+
4
1
2
1
dx
x
x
;
6)
( )
∫
+
e
xx
dx
1
ln1
;
7)
∫
+
1
0
6
2
1
dx
x
x
; 8)
∫
−
+
4
3
2
2
3
dx
x
x
;
9)
(
)
dx
x
x
e
∫
1
lncos
;
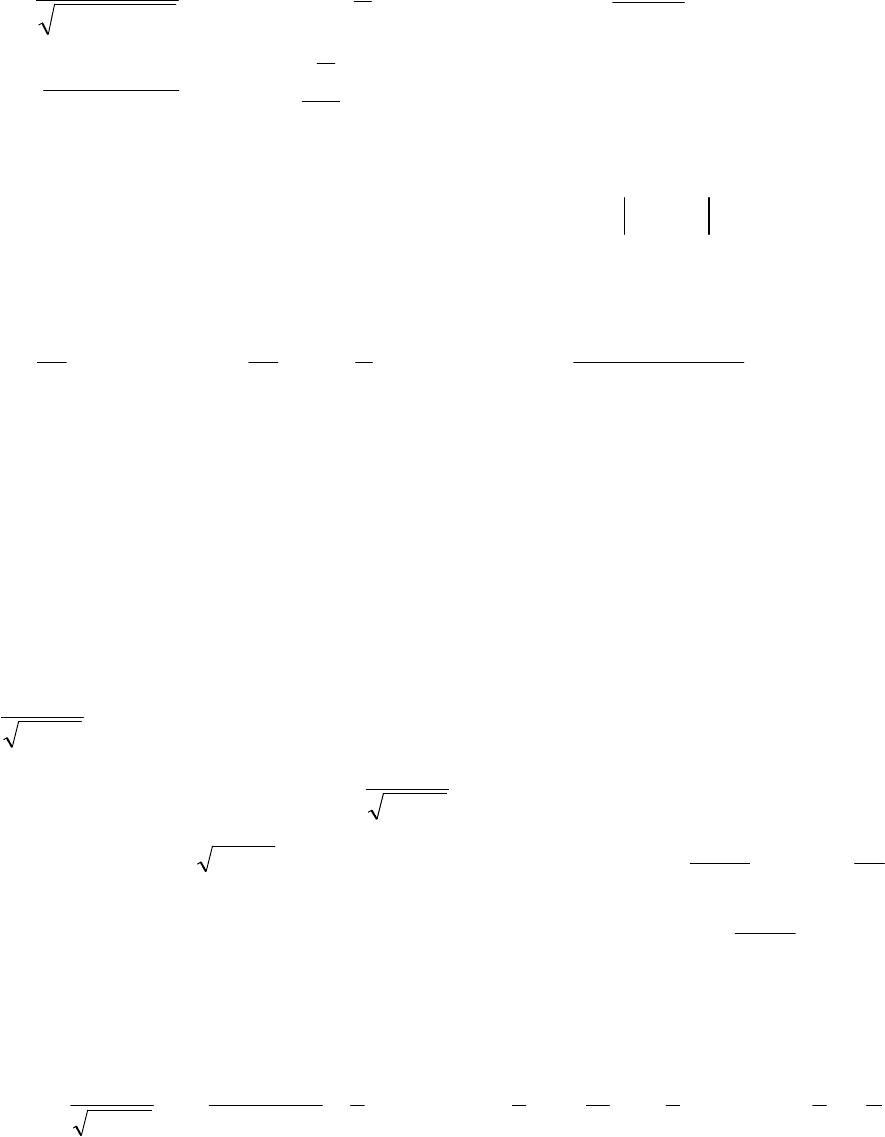
139
10)
∫
−+
1
0
2
23 xx
dx
;
11)
dx
x
2
sin
2
∫
−
π
π
;
12)
∫
+
1
0
2
1
dx
e
e
x
x
;
13)
∫
++
1
0
2
544 xx
dx
;
14)
dx
x
e
x
∫
2
1
3
1
2
.
5.12. Найти:
1)
()
,
2
0
dxxf
∫
если
()
≤<−
≤≤
=
;21,2
,10,
2
xx
xx
xf
2)
dxx
∫
−
2
0
1
.
5.13. Объяснить, почему формальное применение формулы Ньютона-
Лейбница приводит к неверным результатам, если:
а)
∫
−
1
1
x
dx
; б)*
∫
−
x
arctg
dx
d 1
1
1
; в)*
( )
∫
+
π2
0
22
2cos xtgx
dx
2. Замена переменной в определённом интеграле. Если: 1) функция
(
)
xf непрерывна на отрезке
[
]
ba, ; 2) функция
(
)
t
ϕ
дифференцируема, а её
производная
(
)
t
ϕ
′
непрерывна на
[
]
β
α
,
,
(
)
a
=
α
ϕ
,
(
)
b
=
β
ϕ
, тогда справед-
лива формула
()
=
∫
dxxf
b
a
()( ) ()
dtttf ϕϕ
β
α
′
⋅
∫
.
Пример.5.3. Применяя подходящую замену переменной, найти
∫
−
−
1
1
45 x
xdx
.
Решение. Функция
()
x
x
xf
45−
=
определена и непрерывна на отрезке
[
]
1,1
−
. Положим 0,45 ≥=− ttx , отсюда
2
4
5
t
x
=−
,
4
5
2
t
x
−
= ,
2
tdt
dx −= .
При
1
−
=
x
имеем
3
=
t
; при
1
=
x
имеем
1
=
t
. Функция
()
4
5
2
t
t
+
=ϕ удовле-
творяет на отрезке с концами 3; 1 условиям замены переменной (заметь-
те, мы получили
1
3
=
>
=
β
α
, что не изменяет предусмотренный в формуле
порядок замены пределов интегрирования), вычислим:
(
)
( )
6
1
3
1
5915
8
1
|
3
5
8
1
5
8
1
24
5
45
3
1
3
3
1
2
1
3
2
1
1
=
+−−=
−=⋅−=
⋅⋅
⋅−
−=
−
∫∫∫
−
t
tdtt
t
tdtt
x
xdx
.
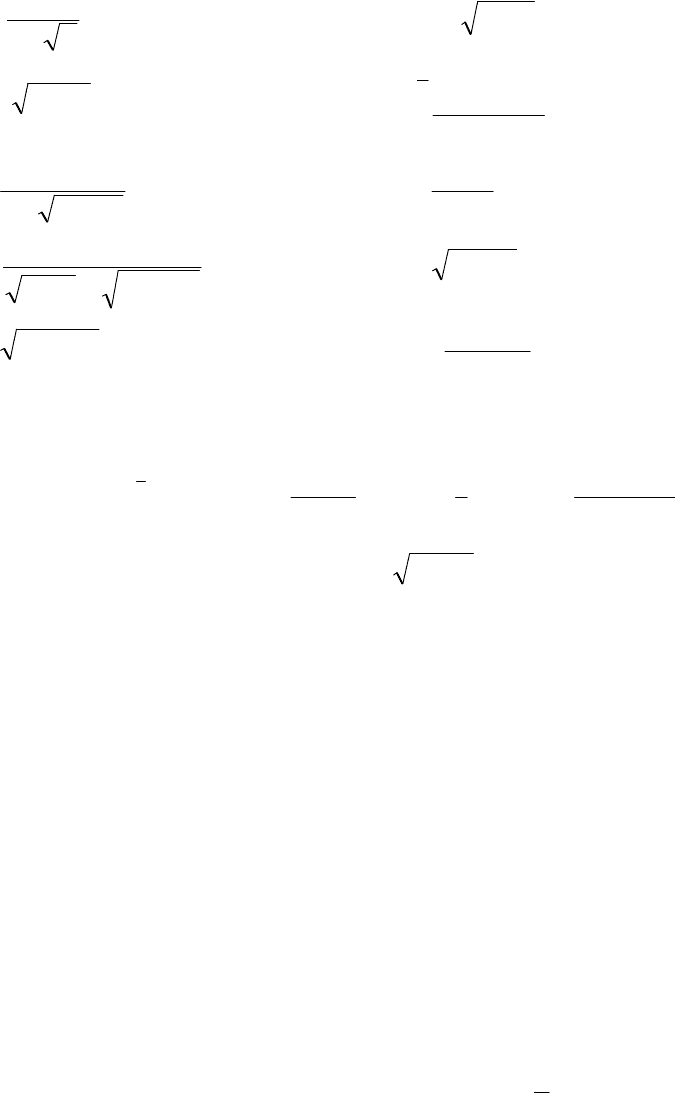
140
5.14. Применяя подходящую замену переменной, вычислить:
1)
∫
+
4
0
1 x
dx
; 2)
dxxx
∫
−⋅
9
1
3
1
;
3)
∫
−
2ln
0
1dxe
x
;
4)
∫
+
2
0
cos23
π
x
dx
;
5)
∫
−+
6
1
231 x
dx
; 6)
∫
+
1
0
1
x
e
dx
;
7)
( )
∫
−
+++
0
2
3
33 xx
dx
;
8)
∫
−
2
0
2
4 dxx
;
9)
dxxx
∫
+
1
0
2
2
; 10)
∫
−
+
1
0
xx
ee
dx
.
5.15. Объяснить, почему формальная замена
x
через
(
)
t
ϕ
приводит к
неверным результатам, если:
а)
∫
−
1
1
dx
,
3
2
x
t
=
;
б)
∫
−
+
1
1
2
1 x
dx
,
t
x
1
= ; в)
∫
+
π
0
2
sin1 x
dx
,
tgx
t
=
.
5.16. Можно ли в интеграле
∫
−
3
0
3
2
1 dxxx положить
t
x
sin
=
?
3. Интегрирование по частям. Если функции
(
)
xu
и
(
)
xv
имеют не-
прерывные производные на отрезке
[
]
ba,
, то
()() ()() ()()
dxxuxvxvxudxxvxu
b
a
b
a
b
a
′
−=
′
∫∫
|
или, в более короткой записи,
duvuvdvu
b
a
b
a
b
a
∫∫
−= |
.
Пример 5.4. Вычислить
∫
−
1
0
dxxe
x
.
Решение. Положим dxedvxu
x−
== , , тогда
x
evdxdu
−
−== , . Функции
x
evxu
−
−== , непрерывны и имеют непрерывные частные производные на от-
резке
[
]
1,0
, применим формулу интегрирования по частям, получим
+⋅−=
−−
∫
1
0
1
0
|
xx
exdxxe =
∫
−
1
0
dxe
x
1
2
|
1
0
1
+−=−−
−−
e
ee
x
.
