Никифорова И.А. Математика в экономике: сборник задач. Часть ?
Подождите немного. Документ загружается.

121
Известны методы определения коэффициентов разложения (4.8). При-
ведём обе части равенства (4.8) к общему знаменателю и, приравнивая затем
числители получившихся дробей, придём к тождеству, в обеих частях которо-
го будут находиться многочлены. По методу неопределённых коэффициентов
далее следует приравнять коэффициенты при одинаковых степенях
x
в обеих
частях тождества, в результате получим систему линейных уравнений относи-
тельно коэффициентов разложения. Решив её, найдём коэффициенты. Можно
составить систему уравнений для определения коэффициентов другим спо-
собом, придавая в тождестве переменной
x
n
различных значений. Обычно,
если многочлен
(
)
Q x
n
имеет действительные корни, целесообразно полагать
x
равным этим корням. Часто бывает полезным комбинировать рассмотренные
способы.
2. Интегрируемость рациональных функций. Рациональные функции
являются интегрируемыми в своих областях определения.
•
Целые рациональные функции (многочлены) интегрируются очевид-
ным образом.
•
Интегрирование неправильных рациональных дробей сводится к ин-
тегрированию целых рациональных функций и правильных рациональных
дробей.
•
Интегрирование правильных рациональных дробей сводится к интег-
рированию простейших дробей.
•
Каждая из простейших дробей интегрируется в элементарных функ-
циях:
1) =
−
∫
dx
a
x
A
CaxA
+
−
ln
;
2)
( ) ( )
)1,(
1
1
1
>∈+
−
⋅
−
=
−
−
∫
nNnC
ax
n
A
dx
ax
A
nn
;
3)
( )
=
++
+
∫
dx
qpxx
NMx
2
( )
( )
=
++
−++
∫
dx
qpxx
p
MNpx
M
2
2
2
2
(
)
( )
+
++
++
∫
qpxx
qpxxdM
2
2
2
=
−+
++
−+
∫
442
2
2
22
2
p
q
p
x
p
x
dxMp
N
(
)
+++ qpxx
M
2
ln
2
=
−+
+
+
−+
∫
42
2
2
2
2
p
q
p
x
p
xd
M
p
N
(
)
+++ qpxx
M
2
ln
2
C
p
q
p
x
arctg
p
q
M
p
N
+
−
+
−
−
4
2
4
2
22
.

122
4)
( )
=
++
+
∫
dx
qpxx
NMx
n
2
(
)
( )
+
++
++
∫
n
qpxx
qpxxdM
2
2
2
=
−+
+
+
−
∫
n
p
q
p
x
p
xd
M
p
N
42
2
2
2
2
(
)
+
−
++
−
n
qpxxM
n
1
2
1
2
+⋅
−
22
p
xJM
p
N
n
,
1
,
>
∈
n
N
n
. Здесь
+=
2
p
xJJ
nn
ин-
теграл, для вычисления которого в примере 4.4 получена рекуррентная фор-
мула.
Напомним, в интегралах 3), 4)
04
2
<− qp
.
Пример 4.5. Выделить целые части следующих дробей:
1)
1
1
2
3
+
++
x
xx
; 2)
x
x
x
xxx
2
233
23
24
−
−
−−−
.
Решение.1) =
+
++
1
1
2
3
x
xx
(
)
=
+
++
1
11
2
2
x
xx
x
+
1
1
2
+
x
.
2) Произведём деление многочленов "уголком":
|233_
24
−−− xxx
xxx 2
23
−−
234
2xxx −−
1
+
x
23_
23
−−− xxx
xxx 2
23
−−
−
−
x 2
,
с учётом этого
−+=
−
−
−−−
1
2
233
23
24
x
x
x
x
xxx
x
x
x
x
2
2
23
−
−
+
.
Пример 4.6. Разложить данные дроби на простейшие:
1)
6
5
1
2
+
−
x
x
;
2)
( )
( )
221
2
2
++− xxx
x
.
Решение. 1) Так как
(
)
(
)
3265
2
−−=+− xxxx
, то искомое разложение
имеет вид
( ) ( )
32
65
1
2
−
+
−
=
+−
x
B
x
A
xx
.
Приведём дроби к общему знаменателю и, приравнивая числители дро-
бей, получим
(
)
(
)
132
=
−
+
−
xBxA
или
(
)
(
)
132
=
+
−
+
BAxBA
. (4.9)
По методу неопределённых коэффициентов составим систему, прирав-
нивая коэффициенты при одинаковых степенях
x
:
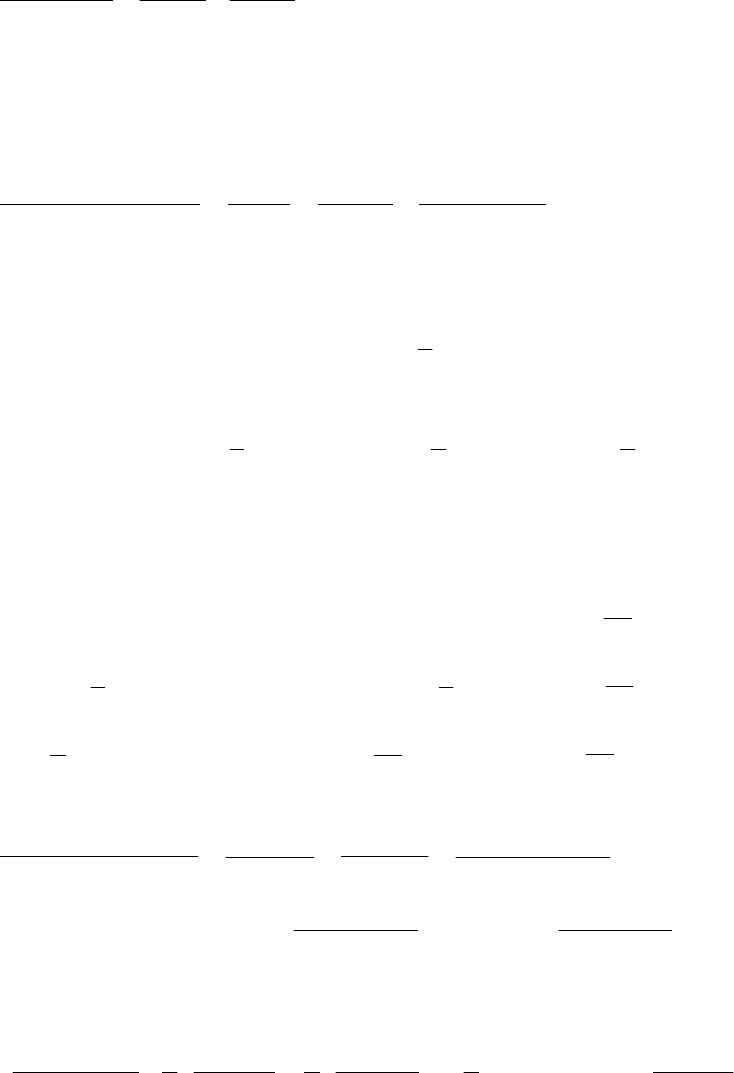
123
⇔
=+
−=+
.0:
,132:
1
0
BAx
BAx
⇔
−=
−=
.1
,
B
BA
−=
=
.1
,1
B
A
Подставим найденные значения коэффициентов, выпишем ответ:
( ) ( )
3
1
2
1
65
1
2
−
−
−
=
+−
xx
xx
.
Замечание. Коэффициенты разложения можно найти иначе: полагая в
тождестве (4.9)
3
=
x
, получим
1
=
A
; полагая
2
=
x
, найдём
1
−
=
B
.
2) Поскольку дискриминант квадратного трёхчлена в знаменателе
044
2
<−=− qp
, то разложение дроби на простейшие имеет вид
( )
( )
=
++− 221
2
2
xxx
x
( )
+
−1x
A
( )
+
−
2
1x
B
(
)
22
2
++
+
xx
DCx
,
отсюда придём к тождеству:
x
=
(
)
(
)
BxxxA +++− 221
2
(
)
+++ 22
2
xx
(
)
(
)
2
1−+ xDCx .
При
1
=
x
имеем
1
5
=
B
, т.е.
5
1
=B . С учётом этого после раскрытия
скобок и приведения подобных тождество примет вид
=
x
(
)
+⋅+
3
xCA +⋅
−++
2
2
5
1
xCDA +⋅
−+ xDC 2
5
2
−+ AD 2
5
2
.
Для определения трёх оставшихся коэффициентов составим систему,
приравнивая в тождестве коэффициенты при любых трёх одинаковых степе-
нях
x
:
⇔
=−+
=−++
=+
.12
5
2
:
,02
5
1
:
,0:
1
2
3
DCx
CDAx
CAx
⇔
=
−−=
−=
.
25
1
,
5
1
3
,
A
AD
AC
=
−=
−=
.
25
1
,
25
8
,
25
1
A
D
C
Таким образом, имеем
( )
( )
=
++− 221
2
2
xxx
x
( )
+
−125
1
x
( )
−
−
2
15
1
x
( )
2225
8
2
++
+
xx
x
.
Пример 4.7. Найти: 1)
∫
+
+
8
8
2
2
x
x
dx
; 2) dx
x
x
x
∫
+
+
−
5
2
1
2
.
Решение. 1) Подынтегральная дробь является правильной и, так как
(
)
2
2
42882 +=++ xxx
, то она является простейшей:
∫
+
+
8
8
2
2
x
x
dx
=
( )
=
+
∫
2
2
2
1
x
dx
(
)
( )
( )
( )
C
x
Cx
x
xd
+
+
−=++−=
+
+
−
∫
22
1
2
2
1
2
2
2
1
1
2
.
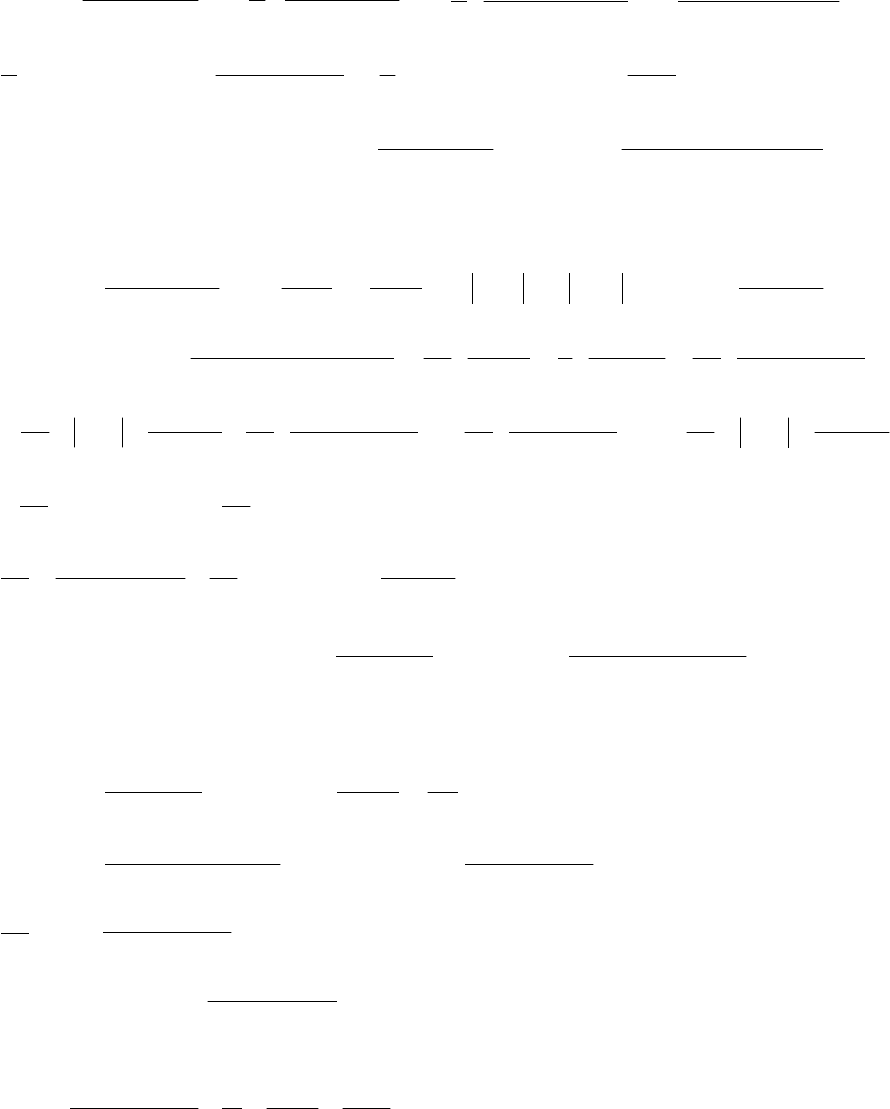
124
2) Подынтегральная дробь, очевидно, является правильной. Дискрими-
нант квадратного члена в знаменателе
0162044
2
<−=−=− qp
, дробь про-
стейшая типа 3):
2
1
5
2
1
2
=
+
+
−
∫
dx
x
x
x
(
)
=
+
+
−
+
∫
dx
x
x
x
5
2
412
2
(
)
( )
=
+++
−
++
++
∫∫
412
2
52
52
2
1
22
2
xx
dx
xx
xxd
(
)
(
)
( )
=
++
+
−++
∫
2
2
2
21
1
252ln
2
1
x
xd
xx
(
)
C
x
arctgxx +
+
−++
2
1
52ln
2
1
2
.
Пример 4.8. Найти: 1) dx
x
x
∫
+
−
6
5
1
2
; 2)
( )
( )
∫
++− 221
2
2
xxx
xdx
.
Решение. Подынтегральные дроби правильные, воспользуемся разложе-
нием их на простейшие (см. пр.4.6) .
1)
∫∫
−
−
=
+
−
3
6
5
1
2
x
dx
dx
x
x
∫
=
−
2
x
dx
=
+
−
−
−
Cxx ln2ln3ln
(
)
( )
2
3
ln
−
−
x
xC
;
2)
( )
(
)
=
++−
∫
221
2
2
xxx
xdx
( )
+
−
∫
125
1
x
dx
( )
−
−
∫
2
1
5
1
x
dx
( )
=
++
+
∫
dx
xx
x
22
8
25
1
2
( )
( )
(
)
( )
=
++
+
−
++
+
−
−
−−=
∫∫
11
1
25
7
22
22
50
1
15
1
1ln
25
1
22
x
xd
dx
xx
x
x
x
( )
−
−
−−
15
1
1ln
25
1
x
x
(
)
( )
=++−++− Cxarctgxx 1
25
7
22ln
50
1
2
(
)
( )
( )
( )
C
x
xarctg
xx
x
+
−
−+−
++
−
15
1
1
25
7
22
1
ln
50
1
2
2
.
Пример 4.9. Найти: 1) dx
x
xx
∫
+
++
1
1
2
3
; 2) dx
x
x
x
xxx
∫
−
−
−−−
2
233
23
24
.
Решение. В обоих примерах подынтегральные дроби неправильные, це-
лые части дробей выделены ранее при решении пр. 4.5:
1) =
+
+=
+
++
∫ ∫∫
1
1
1
22
3
x
dx
xdxdx
x
xx
Carctgx
x
++
2
2
.
2)
( )
∫∫
−+=
−
−
−−−
dxxdx
x
x
x
xxx
1
2
233
23
24
=
−
−
+
∫
dx
x
x
x
x
2
2
23
−+ x
x
2
2
dx
x
x
x
x
∫
−
−
+
2
2
23
.
Дробь
x
x
x
x
2
2
23
−
−
+
правильная. Преобразуем знаменатель:
=−−
x
x
x
2
23
(
)
=−− 2
2
xxx
(
)
(
)
12
+
−
xxx
. Разложим дробь на простейшие:
x
x
x
x
2
2
23
−
−
+
=
1
2
+
+
−
+
x
D
x
B
x
A
.
Отсюда придём к тождеству
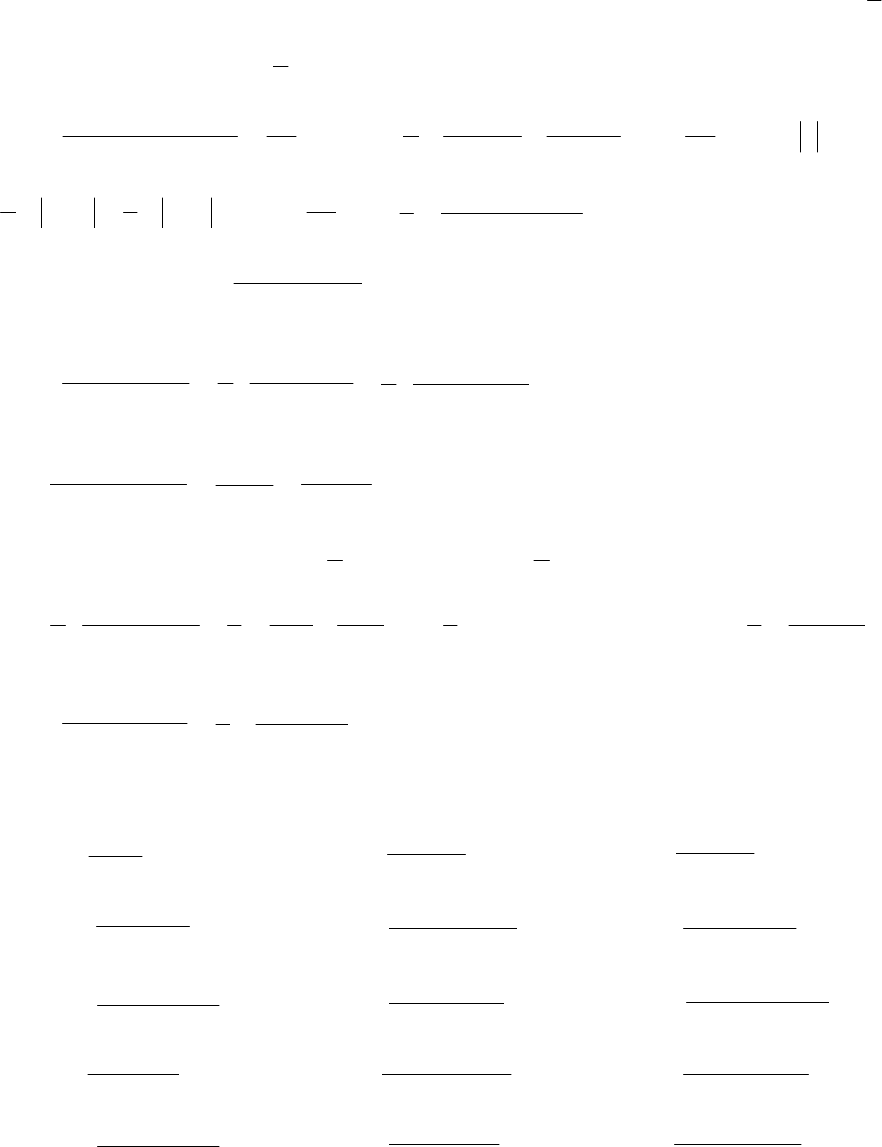
125
(
)
(
)
(
)
(
)
21122
−
⋅
⋅
+
+
⋅
⋅
+
+
⋅
−
=
+
xxDxxBxxAx
.
Полагая в тождестве
0
=
x
, получим
1
−
=
A
; при
1
−
=
x
найдём
3
1
=D ;
при
2
=
x
вычислим
3
2
=B . Подставляя найденные значения, получим
=
−
−
−−−
∫
x
x
x
xxx
2
233
23
24
−+ x
x
2
2
( ) ( )
∫
=
+
+
−
+− dx
xxx 13
1
23
21
++ x
x
2
2
−
xln
−−− 2ln
3
2
x =++ Cx ln1ln
3
1
++ x
x
2
2
( )( )
12
ln
3
1
2
3
+− xx
Cx
.
Пример 4.10.*
.
5
6
24
∫
+
+
x
x
xdx
Решение. Сделаем подстановку
xdxdtxt 2,
2
==
, получим
=
+
+
∫
5
6
24
x
x
xdx
∫
=
+
+
5
6
2
1
2
t
t
dt
( )( )
∫
++
.
512
1
tt
dt
Разложим подынтегральную дробь на простейшие:
( )( )
1
15
tt
=
++
()
+
+1t
A
( )
15
B
⇒
+
(
)
(
)
151
+
+
+
=
tBtA
.
Подставим
4
1
1 =⇒−= At ;
4
1
5 −=⇒−= Bt . С учётом этого
( )( )
( ) ( )( )
(
)
( )
∫ ∫
+
+
=++−+=
+
−
+
=
++
.
5
1
ln
8
1
ln5ln1ln
8
1
5
1
1
1
8
1
512
1
t
tC
Cttdt
tttt
dt
Возвращаясь к старой переменной, получим
=
++
∫
5
6
24
x
x
xdx
(
)
.
5
1
ln
8
1
2
2
+
+
x
xC
Найти интегралы.
4.106.
.
3
∫
−
x
dx
4.107.
( )
.
32
∫
+x
dx
4.108.
( )
.
5
4
∫
+x
dx
4.109.
( )
.
15
3
∫
+x
dx
4.110. .
2
4
2
2
∫
+
+
x
x
dx
4.111. .
9
6
2
∫
+
−
x
x
dx
4.112. .
5
4
2
∫
+
−
x
x
dx
4.113. .
2
2
2
∫
+
+
x
x
dx
4.114.
( )( )
.
32
4
dx
xx
x
∫
−−
−
4.115.
( )
.
5
1
dx
xx
∫
+⋅
4.116.
( )( )
.
23
dx
xx
x
∫
++
4.117.
( )( )
.
21
12
dx
xx
x
∫
−−
−
4.118. .
5
4
2
∫
−
+
x
x
dx
4.119.
.
2
72
2
∫
−
+
+
dx
x
x
x
4.120.
.
4
6
2
67
2
∫
+−
−
dx
x
x
x

126
4.121.
.
3
2
23
2
∫
−
+
+
dx
x
x
x
4.122.
( )( )
.
11
323
2
dx
xxx
xx
∫
+−⋅
−+
4.123.
( )( )( )
.
321
∫
++⋅− xxx
dx
4.124.
.
2
2
23
2
∫
−
+
+
dx
x
x
x
x
4.125.
( )
( )
.
91
23
2
∫
−+
−
dx
xx
x
4.126. .
2
2
23
∫
−
+
dx
x
x
x
4.127.
( )( )
.
31
2
2
∫
++ xx
dxx
4.128.
(
)
( )( )
.
21
1611
2
∫
+−
+
xx
dxx
4.129. .
4
4
85
23
∫
+
−
−
⋅
dx
x
x
x
x
4.130. .
1
3
∫
+
x
xdx
4.131.
( )
( )
.
11
2
2
∫
++ xx
dx
4.132.
.
8
3
∫
−
dx
x
x
4.133. .
2
3
∫
−
dx
x
x
4.134.
.
2
23
4
∫
−
+
dx
x
x
x
4.135.
.
4
2
3
3
∫
−
+
dx
x
x
x
4.136.
(
)
.
1
2
3
∫
−
+
dx
x
x
x
4.137.
.
8
6
4
2
3
∫
+
−
+
dx
x
x
x
4.138.
.
323
3
3
∫
−
−+
dx
x
x
xx
4.139.
.
4
4153
3
23
∫
+
+++
dx
x
x
xxx
4.140.
.
1
3
3
533
23
234
∫
+
+
+
−++
dx
x
x
x
xxx
4.141.
.
6
11
6
4
23
∫
+
+
+
+
dx
x
x
x
x
4.142.
(
)
.
1
2
1
24
∫
+
+
+
x
x
dxx
4.143.
.
1
1
4
4
∫
−
+
dx
x
x
4.144.
( )
.
2
35
2
2
dx
x
x
∫
+
+
4.145.
.
4
4
1
24
∫
+
+
+
dx
x
x
x
4.146.*
.
1
4
∫
+
x
dx
4.147. Используя различные приёмы, найти интегралы.
1)
∫
+
+
5
6
24
x
x
xdx
;
2)
( )
∫
+
−
dx
x
xx
9
2
1
; 3)
(
)
(
)
∫
−+
dx
xx
x
11
44
7
;
4)
(
)
∫
+
2
6
1xx
dx
;
5)
∫
+
57
x
x
dx
;
6)
dx
x
x
xx
∫
−
+
+
2
39
25
.
4.5. Интегрирование тригонометрических функций
Пусть
(
)
−
vuR , рациональная функция двух переменных
v
u
,
, т.е.
функция, содержащая переменные
v
u
,
и постоянные, над которыми произво-
дятся операции сложения, вычитания, умножения и деления.
1. Интегралы вида
(
)
dxxxR
∫
⋅cos,sin
сводятся к интегралам от рацио-
нальных функций при помощи универсальной тригонометрической подста-
новки:
⇒<<−=
,,
2
ππ xt
x
tg
sin x
t
t
=
+
2
1
2
, cos x
t
t
=
−
+
1
1
2
2
,
x arctgt
=
2
,
dx
dt
t
=
+
2
1
2
.
(4.10)
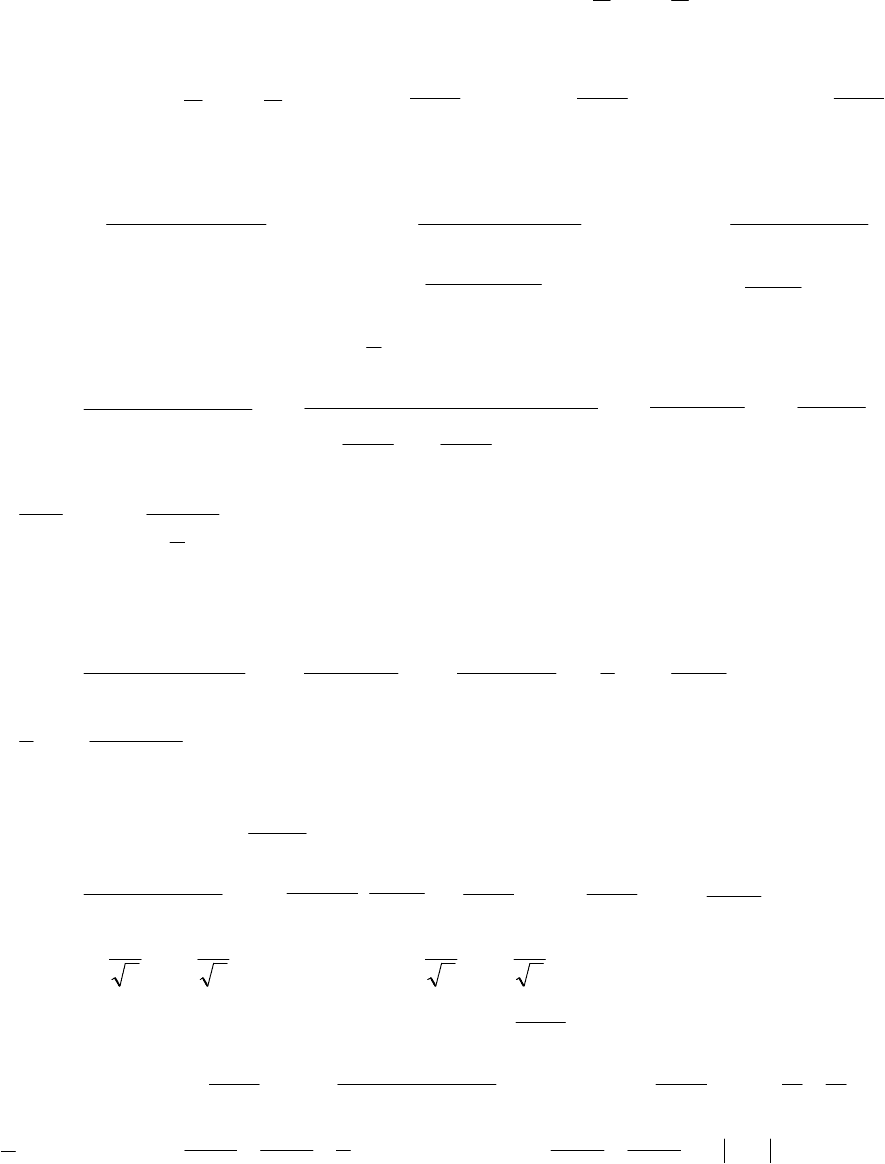
127
Если:
1)
(
)
=− xxR cos,sin
(
)
xxR cos,sin− , то удобно положить
cos
,
x
t
x
=
<
<
0
π
;
2)
(
)
=− xxR cos,sin
(
)
xxR cos,sin− , то
sin ,x t x= − < <
π
π
2
2
;
3)
(
)
=−− xxR cos,sin
(
)
xxR cos,sin , то
()
⇒<<−=
2
2
,
π
π
xtxtg
sin
2
2
2
1
x
t
t
=
+
,
cos
2
2
1
1
x
t
=
+
,
arctgt
x
=
,
dx
dt
t
=
+
1
2
.
Пример 4.11. Найти:
1)
dx
x
x
4
3
5
cos
sin
+
+
∫
; 2)
sin
cos
cos
xdx
x
x
2
2
5
−
+
∫
; 3)
2 3
2
2 2
tgx
x
x
dx
+
+
∫
sin
cos
;
4) ctgxdx
5
∫
;
5)
dx
x
x
sin
cos
2 4
⋅
∫
;
6)
cos
sin
3
6
x
x
dx
∫
.
Решение. 1) Положим
tg
x
t
2
=
. С учётом (4.10) имеем
=
++
∫
5
sin
3
cos
4
x
x
dx
( )
=
+
+
+
⋅+
+
−
⋅
∫
2
22
2
15
1
2
3
1
1
4
2
t
t
t
t
t
dt
2
6
9
2
dt
t
t
+ +
=
∫
( )
2
3
2
dt
t +
=
∫
−
+
+ =
2
3
t
C
−
+
+
2
2
3tg
x
C
.
2) Подынтегральная функция является нечётной относительно
sin
x
.
Положим
,
cos
t
x
=
dtxdx
=
−
sin
, получим
sin
cos
cos
xdx
x
x
2
2
5
− +
=
∫
−
− +
=
∫
dt
t
t
2
2
5
( )
−
− +
=
∫
dt
t 1 4
2
(
)
−
−
+ =
1
2
1
2
arctg
t
C
(
)
−
−
+
1
2
1
2
arctg
x
C
cos
.
3) Подынтегральная функция удовлетворяет условию 3). Применим
подстановку
tgx
t
=
,
dx
x
dt
cos
2
=
:
2 3
2
2 2
tgx
x
x
dx
+
+
=
∫
sin
cos
2 3
2
2 2
tgx
tgx
dx
x
+
+
⋅ =
∫
cos
2 3
2
2
t
t
dt
+
+
=
∫
2
2
2
t
t
dt
+
+
∫
=
+
∫
2
3
2
t
dt
( )
ln t arctg
t
C
2
2
3
2 2
+ + + =
( )
ln .tgx arctg
tgx
C
2
2
3
2 2
+ + +
4) Положим
сtgx
t
=
,
x
arcctgt
=
,
dx
dt
t
=−
+
1
2
, получим
ctgxdx
5
∫
= −
+
=
∫
t
t
dt
5
2
1
−
+ − − +
+
=
∫
t t t t t
t
dt
5 3 3
2
1
− − +
+
=
∫
t t
t
t
dt
3
2
1
− + −
t t
4 2
4
2
( )
1
2
1
2
ln + + =t C
( )
− + − + + =
ctgx ctgx
ctgx C
4 2
2
4
2
1
2
1ln − + + +
ctgx ctgx
x C
4 2
4
2
lnsin .

128
5) Данный интеграл можно найти, используя подстановку
tgx
t
=
, однако
проще предварительно преобразовать подынтегральную функцию, используя
тригонометрическую единицу
cos
sin
2 2
1
x
x
+
=
:
dx
x
x
sin
cos
2 4
⋅
=
∫
(
)
sin cos
sin
cos
2 2
2
2 4
x xdx
x
x
+
⋅
=
∫
sin sin cos cos
sin
cos
4 2 2 4
2 4
2x x x x
x
x
dx
+ ⋅ +
⋅
=
∫
∫∫∫
=++⋅
x
dx
x
dx
x
dx
xtg
222
2
sin
cos
2
cos
Cctgxtgx
xtg
+−+2
3
3
;
6)
cos
sin
3
6
x
x
dx
∫
=
(
)
1
2
6
−
=
∫
sin cos
sin
x x
x
dx
d x
x
d x
x
sin
sin
sin
sin
6 4
− =
∫∫
−
1
5
5
sin
x
− +
1
3
3
sin
x
С
.
4.148. Доказать, что при помощи универсальной тригонометрической
подстановки t
x
tg =
2
интеграл
(
)
dxxxR ⋅
∫
cos,sin всегда приводится к инте-
гралу от рациональной функции переменной
t
.
4.149. Указать наиболее подходящие подстановки для рационализации
функций вида:
а)
(
)
dxxxR
∫
cossin
; б)
(
)
dxtgxR ⋅
∫
;
в)
( )
x
dx
ctgxR
2
sin
∫
;
г)
(
)
dxxxR
∫
⋅
22
cos,sin
; д)
(
)
dxxxR
∫
sincos
;
е)
( )
x
dx
tgxR
2
cos
∫
;
4.150. Найти интегралы:
1)
∫
+
−
x
x
dx
cos
sin
2
3
; 2)
∫
+
2
cos
3
x
dx
;
3)
∫
xdxtg
4
;
4)
∫
+
dx
x
tgx
2
sin
1
; 5)
∫
+
⋅
+
;
cos
12
cos
sin
8
sin
22
x
x
x
x
dx
6)
∫
+
x
x
xdx
sin
sin
cos
2
3
;
7)
∫
+
dx
x
xx
2
cos
sinsin
3
;
8)*
dx
ctgx
ctgx
∫
−
+
1
1
;
9)
∫
x
dx
sin
;
10)
∫
−
x
dx
sin
2
; 11)
∫
−
x
x
dx
22
cos
7
sin
4
; 12)
∫
+
x
xdx
2
cos
4
1
2sin
;
13)
∫
+
x
xdx
sin
1
sin
* ;
14)
(
)
∫
+
+
x
x
dxxx
42
53
sin
sin
coscos
;
15)
∫
−
−
1
sin
cos
2sin
23
x
x
xdx
;
16)
dx
tgx
tgx
∫
−3
; 17)
( )
∫
−+ xxx
dx
sin2cos2sin
; 18)
( )( )
∫
++ 1sin4sin xx
dx
.
2. Интегралы вида
∫
xdxx
nm
cossin
, где
m
и
n
−
целые числа, мож-
но вычислить с помощью преобразований подынтегральной функции, в част-
ности, применением формул понижения:
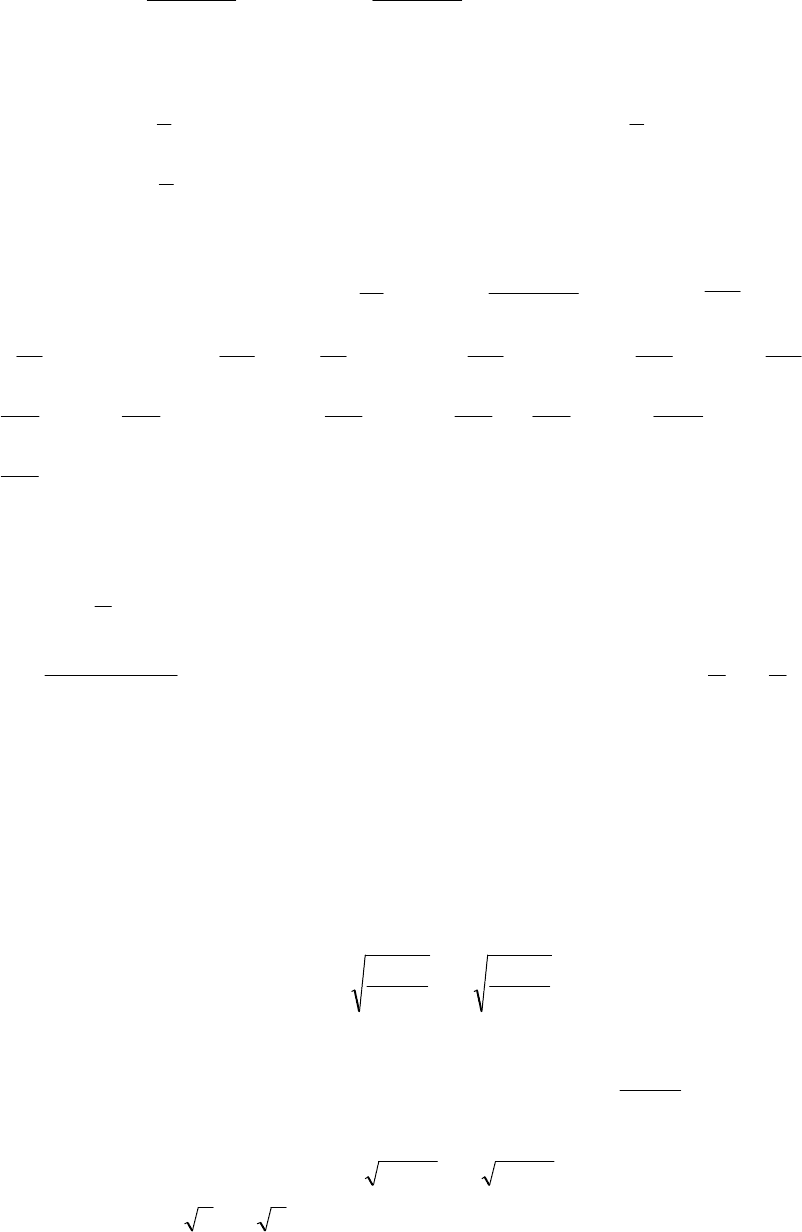
129
sin
cos
2
1 2
2
x
x
=
−
;
cos
cos
2
1 2
2
x
x
=
+
;
2
2
sin
cos
sin
x
x
x
=
.
Интегралы, содержащие произведения функций косинус и синус с раз-
личными аргументами вычисляются с помощью применения формул:
1.
( ) ( )
[ ]
sin sin cos cosα β α β α β⋅ = − − +
1
2
. 2.
( ) ( )
[ ]
cos cos cos cosα β α β α β⋅ = − + +
1
2
.
3.
( ) ( )
[ ]
sin cos sin sinα β α β α β⋅ = − + +
1
2
.
Пример 4.12 . Найти sin cos
4 6
x xdx⋅
∫
.
Решение.
=⋅
+
⋅=⋅
∫∫
dx
x
xxdxx
2
2cos1
2sin
16
1
cossin
464
( )
1
128
1 4
2
− +
∫
cos x dx
+
1
64
2 2
4
sin sinxd x =
∫
1
128
dx
∫
−
1
64
4cos xdx +
∫
1
128
4
2
cos xdx +
∫
1
320
2
5
sin x =
x
128
−
1
256
4sin x +
( )
1
256
1 8+ +
∫
cos xdx
1
320
2
5
sin x =
3
256
x −
1
256
4sin x +
1
2048
8sin x +
1
320
2
5
sin x С+
.
4.151. Найти интегралы:
1)
∫
dx
x
2
cos
4
;
2)
∫
xdx
6
sin
; 3)
∫
xdxx
42
cossin
;
4)
∫
x
x
dx
44
cos
sin
;
5)
∫
xdxxcos5sin
;
6)
∫
dx
xx
3
cos
2
cos ;
7)
∫
xdxx 15sin10sin ; 8)
∫
xdxxx 3cos2coscos ; 9)
∫
xdxx 3cos2sin
2
.
4.6. Интегрирование некоторых иррациональных функций
Пусть
(
)
Rx x
n1
,..., −
рациональная функция
n
переменных
x x
n1
,...,
, т.е.
функция, содержащая переменные
x x
n1
,...,
и постоянные, над которыми про-
изводятся операции сложения, вычитания, умножения и деления.
1. Интеграл вида
Rx
ax b
cx d
ax b
cx d
dx
m m
k
, ,...,
+
+
+
+
∫
1
, где
km m
k
, ,...,
1
−
натураль-
ные,
abcd,,,
−
действительные числа,
ab bc
−
≠
0
, сводится к интегралу от ра-
циональной функции при помощи подстановки
t
s
=
ax b
cx
d
+
+
, где
s
−
наимень-
шее общее кратное чисел
m m
k1
,..., .
В частности, для:
(
)
Rx ax b ax bdx
m m
k
, ,...,+ +
∫
1
используется подстановка
t
s
=
ax b
+
;
(
)
Rx x xdx
m m
k
, ,...,
1
∫
используется подстановка
t
s
=
x
.
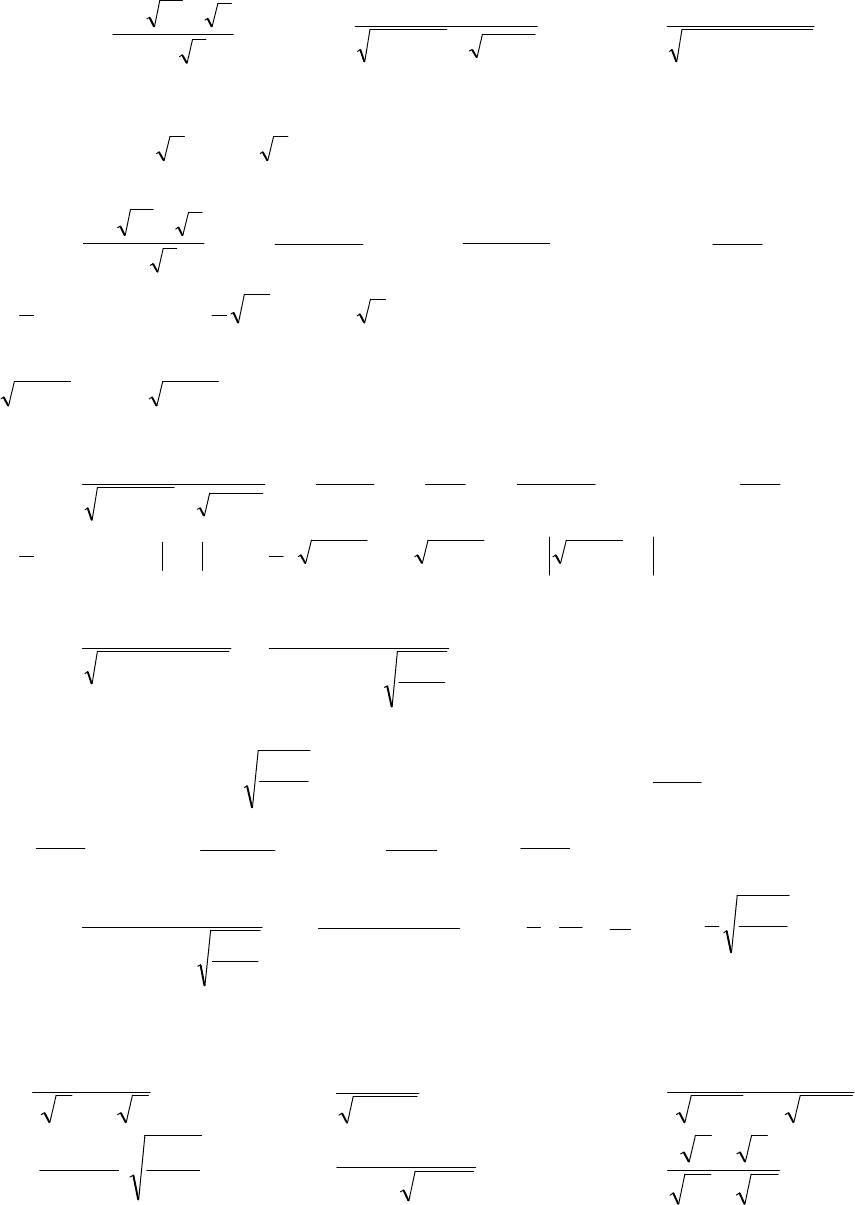
130
Пример 4.13. Найти:
1)
( )
x x x
x x
dx
+ +
+
∫
23
6
3
1
;
2)
( )
dx
x x2 1 2 1
2
3
+ − +
∫
; 3)
( )( )
dx
x x− +
∫
1 2
3 5
4
.
Решение. 1) Подынтегральная функция является рациональной относи-
тельно
x
,
x
3
и
x
6
; m
1
3
=
, m
2
6
=
⇒
s
=
6. Применим подстановку
x t dx tdt= =
6 5
6, , получим
( )
x x x
x x
dx
+ +
+
∫
23
6
3
1
=
( )
6
1
6 4
6 2
5
t t t
t t
tdt
+ +
+
⋅ =
∫
6
1
1
5 3
2
t t
t
dt
+ +
+
=
∫
6
3
tdt +
∫
6
1
2
dt
t
+
=
∫
=++= Carctgtt 6
2
3
4
Cxarctgx ++
6
3
2
6
2
3
.
2) Подынтегральная функция является рациональной относительно
3
12 +x
и
12 +x
⇒
m
1
3
=
,
m
2
2
=
⇒
s
=
6
. Применим подстановку
2 1 3
6 5
x t dx tdt+= =,
, получим
( )
dx
x x2 1 2 1
2
3
+ − +
=
∫
3
5
4 3
tdt
t
t
−
=
∫
3
1
2
tdt
t
−
=
∫
3
11
1
2
t
t
dt
−+
−
=
∫
3 1
1
1
t
t
dt++
−
=
∫
=+−⋅++= Cttt 1ln33
2
3
2
Cxxx +−+⋅++⋅++⋅ 112ln312312
2
3
663
.
3) Преобразуем интеграл:
( )( )
dx
x x− +
=
∫
1 2
3 5
4
( )( )
dx
x x
x
x
+ −
+
−
∫
2 1
2
1
4
.
Подынтегральная функция является рациональной относительно пере-
менной
x
и дроби
x
x
+
−
2
1
4
. Сделаем подстановку
t
x
x
4
2
1
=
+
−
, отсюда найдём
x
t
=
−
+
3
1
1
4
,
( )
dt
t
t
dx
2
4
3
1
12
−
⋅
−= ,
1
3
1
4
−
=−
t
x
x
t
t
+ =
−
2
3
1
4
4
, с учётом этого
( )( )
dx
x x
x
x
+ −
+
−
=
∫
2 1
2
1
4
(
)
( )
∫
=
⋅⋅−
−⋅
− dt
ttt
tt
331
112
424
2
43
− =
∫
4
3
2
dt
t
=+C
t
3
4
4
3
1
2
4
x
x
C
−
+
+
.
4.97. Найти интегралы:
1)
( )
∫
+ xx
dx
4
3
;
2)
∫
−
3
32x
xdx
;
3)
(
)
∫
+−+ 313
4
xx
dx
;
4)
( )
dx
x
x
x
3
2
2
2
2
2
+
−
⋅
−
∫
;
5)
( )
∫
−−
2
11 xx
dx
;
6)
dx
xx
xx
∫
+
+
6
7
4
5
3
;
