Никифорова И.А. Математика в экономике: сборник задач. Часть ?
Подождите немного. Документ загружается.


111
4.35.
dx
x
xctg
∫
−
2
2
cos
23
.
4.36.
dxxtg
∫
2
.
4.37.
∫
+
x
x
dx
2
sin
2
cos
.
4.38.
dx
xx
∫
−
2
2
cos
2
sin
.
Рассмотрим подробнее ситуацию, когда интеграл сводится к таблично-
му посредством введения вспомогательной, зависимой от
x
, переменной ин-
тегрирования. Этот приём иногда называют подведением функции под знак
дифференциала, он является частным случаем метода замены переменной.
Ключевым моментом является тождественное преобразование подынтеграль-
ного выражения с выделением дифференциала новой переменной интегриро-
вания. После освоения приёма введение явно обозначения для новой пере-
менной необязательно.
Пример 4.2. Найти интегралы сведением к табличным :
1)
(
)
∫
+ dxx
10
53
; 2)
∫
xdx2sin
;
3)
∫
⋅ xdxe
x
cos
sin
;
4)
(
)
∫
x
dxx
3
ln
;
5)
∫
−
16
7
1 x
dxx
;
6)
∫
+
x
dx
2
cos
1
.
Решение. 1) Учитывая, что
( )
353 =
′
+x
, положим
(
)
,53
+
=
xu
dx
du
3
=
,
преобразуем интеграл к табличному следующим образом:
(
)
=+
∫
dxx
10
53
1
3
(
)
=⋅+
∫
dxx 353
10
1
3
(
)
(
)
=++
+=
∫
53
10
|5353
xu
xdx =
∫
duu
10
3
1
=+C
u
33
11
(
)
C
x
+
+
=
33
53
11
.
2) По аналогии с предыдущим примером имеем
=
∫
xdx2sin =⋅
∫
dxx 22sin
2
1
( )
=⋅
=
∫
xu
xdx
2
|22sin
2
1
=
∫
udusin
2
1
=+− C
u
2
cos
C
x
+−
2
2cos
.
3) Учитывая, что
(
)
xdxxd cossin
=
, кратко решение запишем в виде
=⋅
∫
xdxe
x
cos
sin
(
)
=⋅
∫
xde
x
sin
sin
C
e
x
+
sin
.
4)
(
)
=
∫
x
dxx
3
ln
( )
∫
=⋅
x
dx
x
3
ln
(
)
(
)
=
∫
xdx lnln
3
(
)
C
x
+
4
ln
4
.
5)
=
−
∫
16
7
1 x
dxx
( )
∫
=
−
2
8
7
1
8
8
1
x
dxx
(
)
( )
∫
=
−
2
8
8
1
8
1
x
xd
Cx +
8
arcsin
8
1
.
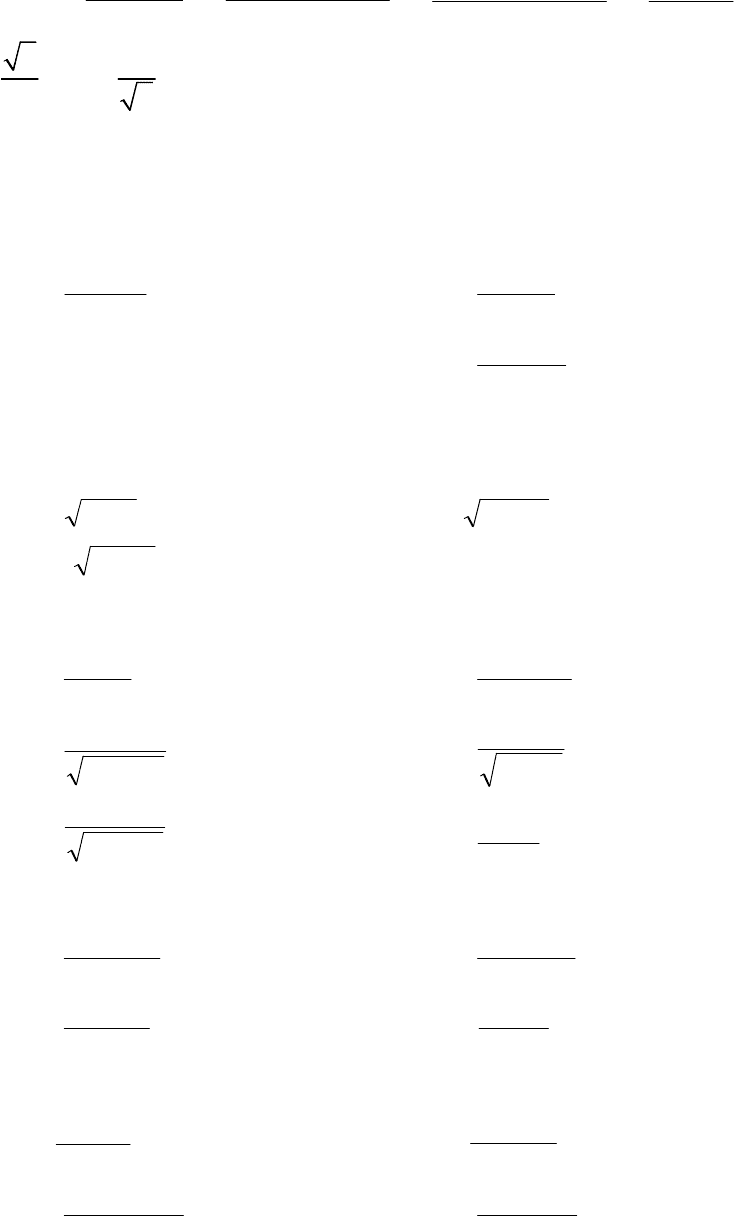
112
6) =
+
∫
x
dx
2
cos
1
=
+
∫
x
x
dx
22
sin
cos
2
( )
=
+⋅
∫
xtgx
dx
22
2cos
(
)
∫
=
+ xtg
tgxd
2
2
2
2
2
tgx
arctgC
=+
.
Найти интегралы:
4.39. dxx
∫
3sin . 4.40. dxx
∫
5cos .
4.41.
∫
x
dx
5
cos
2
.
4.42.
∫
x
dx
7
sin
2
.
4.43. dxe
x
∫
2
.
4.44.
∫
+
2
16
1
x
dx
.
4.45.
(
)
dxx
∫
+32sin . 4.46.
(
)
dxx
∫
−54cos .
4.47.
(
)
dxx
4
56
∫
+ . 4.48.
(
)
dxx
3
32
∫
− .
4.49. dxx
∫
+3 . 4.50. dxx
3
73− .
4.51. dxxx
∫
+5
32
4.52.
(
)
dxxx
∫
−
3
43
21
.
4.53.
∫
dxxe
x
2
. 4.54.
∫
⋅⋅
+−
dxex
x 12
3
.
4.55. dx
x
x
∫
+
5
3
2
. 4.56. dx
x
x
∫
+
⋅
3
2
6
6
5
.
4.57. dx
x
x
∫
−
⋅
5
3
2
74
2
.
4.58. dx
x
x
∫
+
3
2
1
.
4.59.
dx
x
x
∫
−
4
4
1
.
4.60. dx
x
x
∫
+
1
8
3
.
4.61. dxxx
∫
⋅cossin
5
.
4.62. dxxx ⋅⋅+
∫
sin)1(cos
3
.
4.63. dx
x
x
∫
+
2
cos
sin
. 4.64. dx
x
x
∫
+
1
sin
cos
2
.
4.65. dx
x
x
∫
⋅
5
sin
cos4
4.66. dx
x
x
∫
3
cos
sin
4.67.
dxtgx
∫
. 4.68.
dxctgx
∫
.
4.69.
∫
x
xdxtg
2
2
cos
.
4.70. dx
x
сtgx
⋅
+
∫
2
sin
1
.
4.71. dx
x
x
x
∫
⋅
cos
sin
2cos
4.72. dx
x
x
∫
+
2
sin
2sin1

113
4.73.
∫
⋅+
⋅
xtgx
dx
2
cos2
3
.
4.74. dx
x
x
∫
−
2
sin32
2
cos
.
4.75.
dx
e
e
x
x
∫
+
1
.
4.76. dx
e
e
x
x
∫
−
.
3
1
2
2
.
4.77.
dx
x
e
x
∫
−
−
12
12
.
4.78.
dx
x
e
x
∫
.
4.79. dx
x
e
arctgx
∫
+
2
1
. 4.80. dx
x
e
ctgx
∫
⋅
−
2
sin
.
4.81.
dx
x
x
∫
+1
2
.
4.82. dx
x
tgx
∫
2
cos
2
.
4.83. dx
x
x
⋅
∫
ln
.
4.84.
1 2+
∫
ln x
x
dx
4.85.
( )
∫
+⋅ 2ln xx
dx
4.86.
∫
x
x
dx
2
ln
4.87. dx
x
arctgx
∫
+
2
1
. 4.88.
∫
−⋅
25
1arccos xx
dx
.
4.89.
∫
−
⋅+
2
3
1
2arcsin
x
dxx
.
4.90.
(
)
dx
x
arcctgx
∫
+
−
2
100
1
7
.
4.91.
( )
∫
+ xx
dx
9
.
4.92.
∫
⋅
⋅
x
x
x
dx
ln
ln
ln
.
4.93.
dx
xx
x
∫
++
+
3
3
2
13
1
.
4.94. dx
x
xx
∫
+
+
4
3
1
.
4.95.
dx
x
xarctgx
∫
+
+
2
2
1
2
.
4.96.
dx
x
xx
⋅
−
+
∫
2
1
arcsin
4.97.
( )
x
dx
x
xarctg
+
⋅
∫
1
.
4.98. dx
e
e
x
x
∫
−16
2
.
4.99.
dx
x
x
∫
+
4
2
cos
4sin
4
. 4.100.
dx
x
x
x
∫
−
+
⋅
−
1
1
ln
1
1
2
.
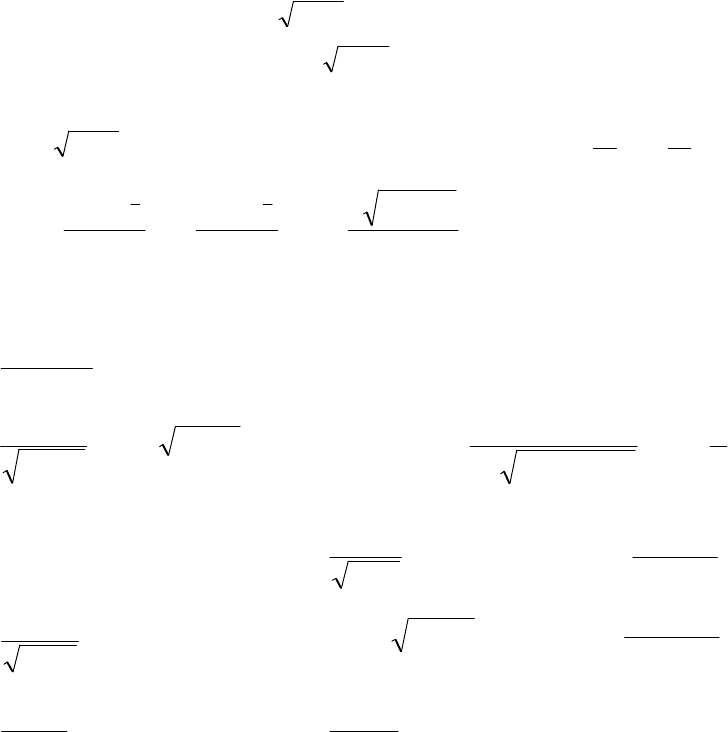
114
4.2. Метод подстановки или замены переменной
Пусть функция
(
)
xf
интегрируема на промежутке
X
, а функция
(
)
tx
ϕ
=
определена и дифференцируема на промежутке
T
и множество её
значений совпадает с
X
, тогда верно равенство
(
)
()
=⋅
=
∫
tx
dxxf
ϕ
|
(
)
(
)
(
)
dtttf ϕϕ
′
⋅
∫
.
(4.1)
Равенство (4.1) называют формулой замены переменной в неопреде-
лённом интеграле. После вычисления неопределённого интеграла при помо-
щи замены переменной необходимо вернуться к исходной переменной.
Формулу (4.1) часто используют "в обратном направлении":
(
)
(
)
(
)
=
′
⋅
∫
dtttf ϕϕ
(
)
dxxf
∫
, где
(
)
tx
ϕ
=
,
или, в других обозначениях,
(
)
(
)
(
)
=
′
⋅
∫
dxxgxgf
(
)
dttf
∫
, где
(
)
xgt
=
.
Пример 4.3. Найти: dxxx
∫
−5 .
Решение. Обозначим
5−= xt
, отсюда
2
5
t
x
=− ,
5
2
+=
t
x
,
tdt
dx
2
=
.
Осуществляя замену переменных, получим
5
2
|5
+=
∫
−
tx
dxxx
=
(
)
=⋅⋅+
∫
tdttt 25
2
(
)
=+
∫
dttt
24
52
C
tt
++
3
10
5
2
35
=
=
( ) ( )
=+
−
+
−
C
xx
3
5
10
5
5
2
2
3
2
5
( )
( )
Cx
x
++
−
103
15
52
3
.
4.101. Применяя указанные подстановки, найти интегралы:
1)
( )
∫
−
⋅
12
3
1x
dxx
,
1
−
=
x
t
;
2)
(
)
dxxx
1023
51
∫
−
,
2
5
1
x
t
−
=
;
3)
∫
+
x
e
dx
3
,
x
et += 3
; 4)
∫
−−⋅
1
2
2
x
x
x
dx
,
x
t
1
= .
4.102. Применяя подходящие подстановки, найти интегралы:
1)
(
)
dxxx
19
15
∫
− ;
2)
dx
x
x
⋅
+
+
∫
1
2
;
3)
( )
∫
−
⋅
7
3 x
dxx
;
4)
∫
−
⋅
x
dxx
2
2
,
5) dxxx
23
1−⋅
∫
;
6)
( )
∫
+
⋅
3
2
5
2 x
dxx
;
7)
∫
−
1
2
x
x
e
dxe
; 8)
∫
+
x
x
e
dxe
2
3
.
115
4.3. Метод интегрирования по частям
Пусть функции
(
)
xu
и
(
)
xv
определены и дифференцируемы, а функ-
ция
(
)
(
)
xuxv
′
⋅
интегрируема на промежутке
X
. Тогда на этом промежутке
интегрируема функция
(
)
(
)
xvxu
′
⋅
, причём справедлива формула
(
)
(
)
(
)
(
)
(
)
(
)
dxxuxvxvxudxxvxu
∫∫
′
⋅−⋅=
′
⋅
.
(4.2)
Формулу (4.2) называют формулой интегрирования по частям в неоп-
ределённом интеграле. Её можно переписать в виде:
duvvudvu ⋅−⋅=⋅
∫∫
.
(4.3)
В формулах (4.2) и (4.3) функция
(
)
−
xv
любая из первообразных
для
(
)
xv
′
.
Метод интегрирования по частям применяется, в частности, в следую-
щих случаях.
1) Для вычисления интегралов вида
(
)
dxexP
bax
n
∫
+
⋅ ,
(
)
(
)
dxbaxxP
n
∫
+⋅cos ,
(
)
(
)
dxbaxxP
n
∫
+⋅sin ,
здесь
N
n
∈
,
−
ba,
действительные числа,
(
)
Px
n
−
многочлен степени
n
относительно переменной
x
. В качестве функции
(
)
xu
следует взять поли-
ном
(
)
xP
n
. Если
1
>
n
, то интеграл
duv⋅
∫
будет принадлежать к тому же ти-
пу, что и исходный, но в нём степень многочлена будет на единицу меньше.
Выбирая этот многочлен в качестве
(
)
xu
, применим формулу интегрирования
по частям вновь и т. д. до тех пор, пока не получим табличный интеграл. В
ходе вычисления перечисленных интегралов формула интегрирования по час-
тям применяется число раз, равное степени многочлена.
2) Если подынтегральное выражение содержит логарифмическую или
одну из обратных тригонометрических функций (за исключением табличных
интегралов и интегралов, которые легко находятся при помощи замены пере-
менных), в качестве
(
)
xu
следует выбрать указанные функции.
3) Для вычисления интегралов вида
dxbxe
ax
∫
⋅sin , dxbxe
ax
∫
⋅cos ,
(
)
dxxlnsin
∫
,
(
)
dxxlncos
∫
,
здесь
ab,
−
действительные числа. Выбор
u
и
dv
в первых двух инте-
гралах произволен, в двух последних - очевиден. При вычислении каждого из
перечисленных интегралов метод интегрирования по частям применяется
дважды, в результате получается выражение, содержащее исходный интеграл.
Следует приравнять интеграл найденному выражению и из составленного
уравнения найти интеграл (см. пр. 4.3.4)).
Пример 4.3. Найти интегралы: 1)
dxxx
∫
⋅cos
;
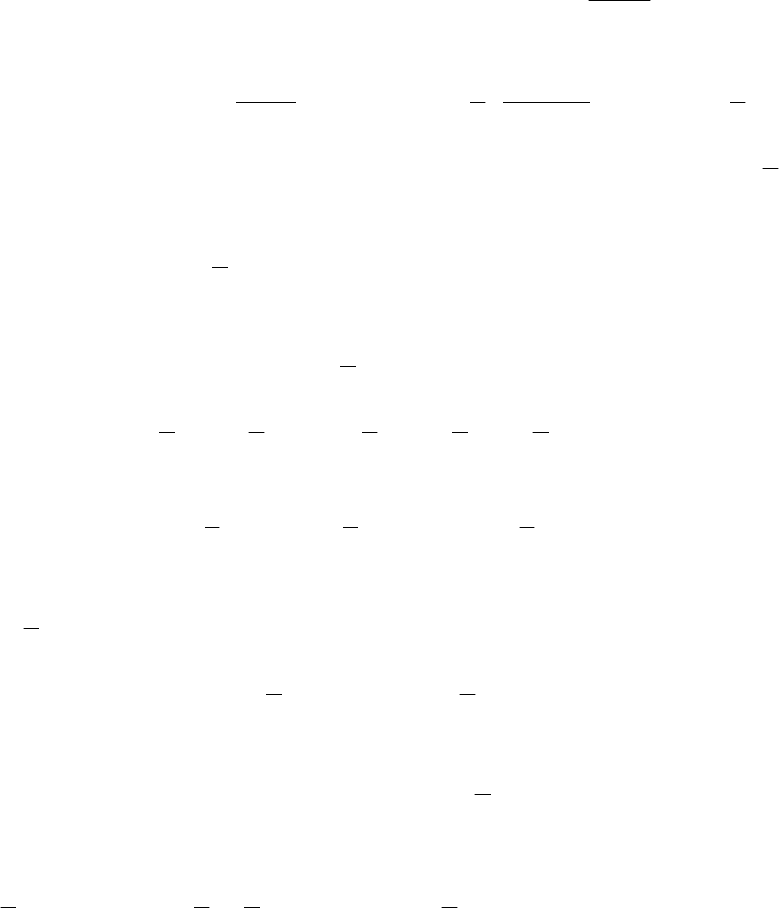
116
2) dxarctgx⋅
∫
;
3)
(
)
dxex
x
∫
⋅+
22
1 ; 4)
(
)
dxxe
x
∫
+⋅ 12cos
3
.
Решение. 1) Положим
x
u
=
,
xdx
dv
cos
=
, тогда
dx
du
=
,
x
v
sin
=
. По
формуле интегрирования по частям получим
∫∫
++=−⋅=⋅ Cxxxxdxxxdxxx cossinsinsincos .
2) Положим
arctgx
u
=
,
dx
dv
=
, тогда
2
1
x
dx
du
+
= ,
x
v
=
. По формуле
интегрирования по частям получим
=
+
−⋅=
∫∫
dx
x
x
arctgxxdxarctgx
2
1
(
)
=
+
+
−⋅
∫
2
2
1
1
2
1
x
xd
arctgxx
(
)
Cxarctgxx ++−⋅
2
1ln
2
1
.
3) Положим
1
2
+=
x
u
,
dx
e
dv
x2
=
, тогда
xdx
du
2
=
,
x
ev
2
2
1
= . При-
меним формулу интегрирования по частям:
(
)
dxex
x
∫
+
22
1
=
(
)
dxxeex
xx
∫
−+
222
1
2
1
.
К последнему интегралу вновь применим формулу (4.3), полагая
x
u
=
,
dx
e
dv
x2
=
. Тогда
dx
du
=
,
x
ev
2
2
1
= , следовательно,
dxxe
x
∫
2
= dxexe
xx
∫
−
22
2
1
2
1
=
( )
xxx
exexe
222
12
4
1
4
1
2
1
−=− .
В итоге
(
)
x edx
x2 2
1+
∫
=
( )
1
2
1
2 2
x e
x
+ −
( )
( )
1
4
2 1
1
4
2 2 3
2 2 2
x e C x x e C
x x
− + = − + + .
4) Положим
x
e
u
3
=
,
(
)
dxxdv 12cos
+
=
, тогда
dx
e
du
x3
3
=
,
( )
12sin
2
1
+= xv . Применим формулу интегрирования по частям:
(
)
dxxe
x
∫
+⋅ 12cos
3
=
( ) ( )
∫
+⋅−+⋅ dxxexe
xx
12sin
2
3
12sin
2
1
33
.
Для нахождения последнего интеграла положим
x
e
u
3
=
,
(
)
dxxdv 12sin
+
=
, тогда
dx
e
du
x3
3
=
,
( )
12cos
2
1
+−= xv
и, значит,
(
)
dxxe
x
∫
+⋅ 12cos
3
=
=
( ) ( ) ( )
1
333
12cos
2
3
12cos
2
1
2
3
12sin
2
1
Cdxxexexe
xxx
+
+⋅++⋅−−+⋅
∫
.
Разрешим последнее равенство относительно искомого интеграла, по-
лучим
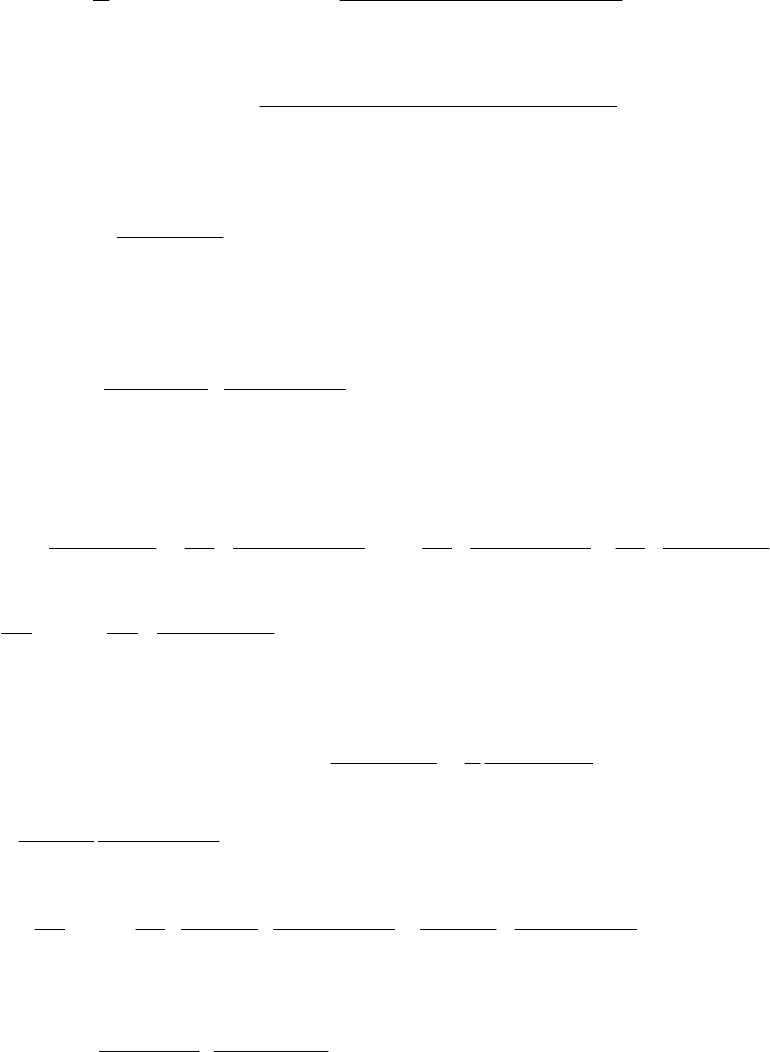
117
+
4
9
1
(
)
dxxe
x
∫
+⋅ 12cos
3
=
(
)
(
)
(
)
1
3
4
12cos312sin2
Ce
xx
x
+
+
+
+
или
(
)
dxxe
x
∫
+⋅ 12cos
3
=
(
)
(
)
(
)
13
12cos312sin2
3
Cxxe
x
++++
.
Пример 4.4.* Показать, что для интеграла
( )
,
22
∫
+
=
n
n
ax
dx
J
,
1
,
>
∈
n
N
n
−
a
постоянная,
,
0
≠
a
1) верна рекуррентная формула
( )
( )
( )
⋅−+
+
−
=
−
−
1
1
22
2
32
12
1
n
n
n
Jn
ax
x
na
J ;
(4.4)
2)
N
n
∈
∀
интеграл
n
J
вычисляется в элементарных функциях.
Решение. Преобразуем интеграл
n
J
следующим образом
( ) ( )
=
+
−+
=
+
=
∫∫
dx
ax
xxa
a
ax
dx
J
nn
n
22
222
2
22
1
( ) ( )
=
+
−
+
∫∫
−
dx
ax
x
a
ax
dx
a
nn
22
2
21
22
2
11
( )
2
1
22
22
11
n
n
xdx
J
aa
xa
−
=−
+
∫
.
К последнему интегралу применим метод интегрирования по частям,
полагая
x
u
=
,
( )
(
)
( )
nn
ax
axd
ax
xdx
dv
22
22
22
2
1
+
+
=
+
= . Тогда
dx
du
=
,
( )
( )
1
22
1
12
1
−
+
−
=
n
ax
n
v
и, следовательно,
( )
( )
( )
( )
+
−
−
+
⋅
−
−=
∫
−−
−
1
22
1
22
2
1
2
12
1
12
111
nn
nn
ax
dx
n
ax
x
n
a
J
a
J
.
Отсюда получаем
( )
( )
( )
⋅−+
+
−
=
−
−
1
1
22
2
32
12
1
n
n
n
Jn
ax
x
na
J
,
что и требовалось показать.
2) При
1
=
n
имеем
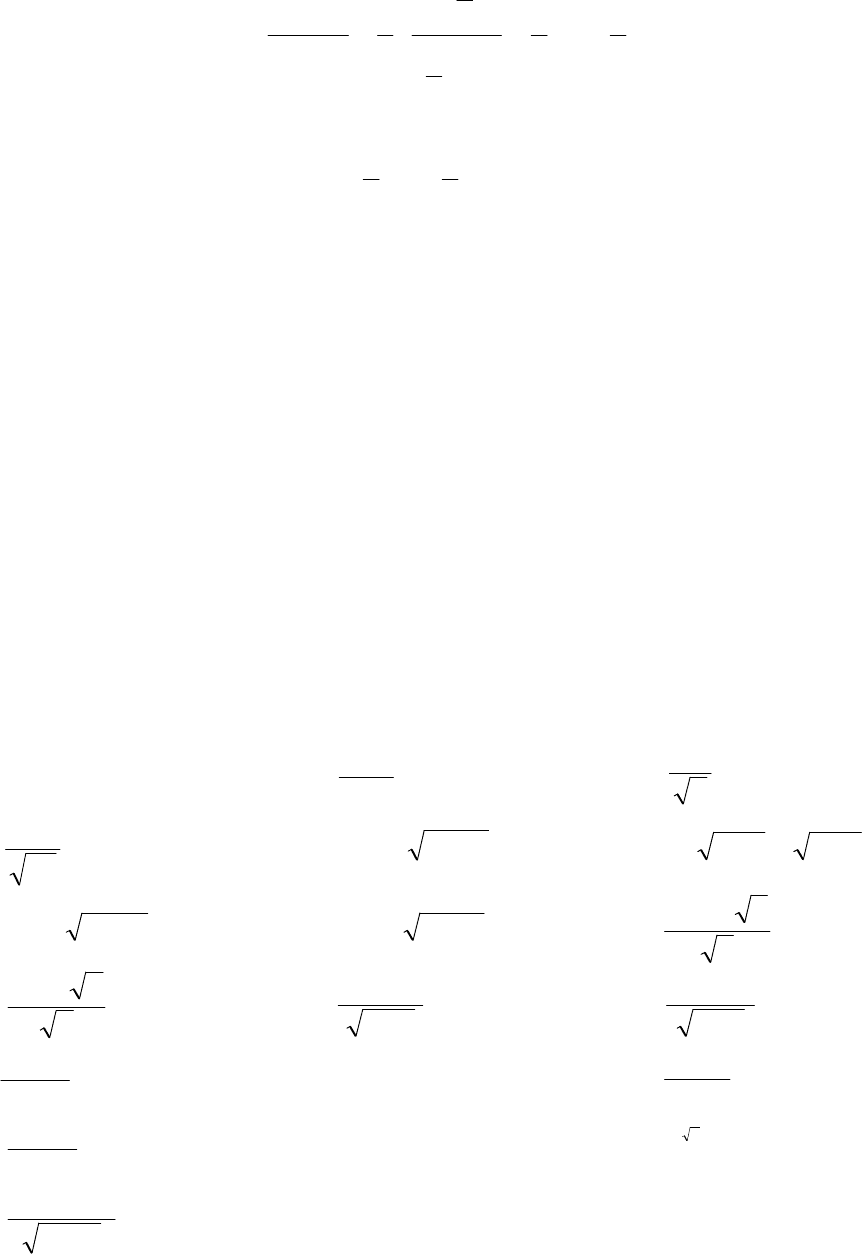
118
=
+
=
+
=
∫ ∫
1
1
222
1
a
x
a
x
d
a
ax
dx
J
,
1
C
a
x
arctg
a
+
т.е.
=
1
J
C
a
x
arctg
a
+
1
.
(4.5)
Зная
1
J
, можно последовательно при помощи рекуррентной формулы
(4.4 ) вычислить
2
J
,
J
3
и т.д. Т. о., используя формулы (4.4), (4.5), можно
вычислить интеграл
J
n
N
n
∈
∀
в элементарных функциях.
4.103. Применяя формулу интегрирования по частям, найти интегралы:
1)
∫
⋅ xdxx sin ; 2)
(
)
∫
⋅
+
xdxx cos12
;
3)
(
)
∫
⋅+ dxex
x
3 ;
4)
∫
⋅ dxx
x
3
;
5)
∫
xdxln
; 6)
∫
xdx
5
log
;
7)
∫
xdxarcsin
; 8)
∫
⋅
arcctgxdxx
,
9)
∫
⋅ xdxx cos
2
;
10)
∫
⋅ xdxx sin
2
; 11)
(
)
∫
⋅+ dxxx
x
2
2
; 12)
∫
⋅ dxex
x2
;
13)
(
)
∫
⋅
+
xdxx 2sin1
; 14)
∫
⋅
xdxx 6cos
; 15)
(
)
(
)
∫
−+ dxxx 75cos1 ;
16)
(
)
(
)
∫
+
⋅
−
dxxx 15sin32 ;
17)
∫
−
⋅ dxex
x
; 18)
∫
⋅ dxex
x7
;
19)
(
)
∫
⋅− dxex
x3
34 ; 20)
(
)
∫
⋅+ dxex
x2
35 ;
21)
∫
⋅ xdxx ln ;
22)
(
)
∫
+− xdxxx ln1
2
;
23)
(
)
∫
+ dxx 14ln
2
24)
(
)
∫
⋅+ dxx 4ln
2
25)
∫
xdx
2
ln ;
26)
∫
dx
x
x
2
2
ln
;
27)
∫
dx
x
x
3
ln
;
28)
∫
dx
x
x
3
2
2
ln
;
29)
(
)
∫
++ dxxx
2
1ln ;
30)
(
)
∫
++− dxxx 11ln
31)
∫
− dxxarctg 14 ; 32)
∫
− dxxarctg 15 ;
33)
∫
dx
x
xarcsin
;
34)
∫
dx
x
xarctg
;
35)
∫
+
dx
x
x
1
arcsin
; 36)
∫
−
dx
x
x
1
arccos
;
37)
∫
dx
x
xx
3
cos
sin
;
38)
∫
⋅ xdxx
2
sin ;
39)
∫
dx
x
x
2
sin
;
40)
∫
dx
x
x
2
cos
;
41)
∫
−
⋅ dxex
x
2
3
;
42)
∫
dxe
x
;
43)
∫
−
dx
x
xx
2
1
arccos
;
44)
∫
xdx
2
arcsin ; 45)
(
)
∫
dxxlncos ;

119
46)
(
)
∫
dxx2lnsin ;
47)
∫
⋅ xdxe
x
sin ; 48)
∫
⋅ xdxe
x
cos ;
49)
∫
⋅ xdxe
x
3cos
2
;
50)
∫
−⋅ dxxe
x
4
2sin
3
π
;
51) 16)
∫
⋅ bxdxe
ax
sin
)
(
−
b
a
,
параметры);
52)*
∫
− dxxa
22
(
−
>
0
a
параметр); 53)*
∫
dx
x
x
2
sin
sinln
.
4.104. Используя метод интегрирования по частям, получить рекур-
рентные формулы для вычисления интегралов (здесь
N
n
∈
):
1) dxexJ
axn
n
∫
= , (
−
a
параметр,
0
≠
a
); 2) xdxJ
n
n
∫
= ln ;
3) xdxJ
n
n
∫
= sin ,
2
>
n
; 4) xdxJ
n
n
∫
= cos ,
2
>
n
;
5)
∫
=
x
dx
J
n
n
sin
,
2
>
n
; 6)
∫
=
x
dx
J
n
n
cos
,
2
>
n
.
4.105. Используя рекуррентные формулы, полученные при решении
предыдущего примера, найти интегралы:
1)
dxex
x−
∫
5
; 2)
xdx
∫
4
ln
;
3)
xdx
∫
3
sin
;
4) xdx
∫
4
cos ;
5)
∫
x
dx
4
sin
; 6)
∫
x
dx
5
cos
.
4.4. Интегрирование рациональных функций
1. Определение рациональной функции. Способы разложения ра-
циональных дробей. Рациональными называют функции, представимые в ви-
де отношения
(
)
()
xQ
xP
n
m
, где
(
)
Px
m
и
(
)
−
xQ
n
многочлены степеней
m
и
n
со-
ответственно относительно переменной
x
:
(
)
m
mm
xaxaaxP ⋅++⋅+= ...
10
,
(
)
xQ
n
n
n
xbxbb ⋅++⋅+= ...
10
, здесь
,,...,,
10 m
aaa
−
n
bbb ,...,
10
действительные
числа, коэффициенты многочленов,
m
,
−
n
целые неотрицательные.
При
0
=
n
рациональную функцию
(
)
()
xQ
xP
n
m
(в этом случае - многочлен) на-
зывают целой; при
n
m
<
-- правильной дробью, при
n
m
≥
− неправильной ра-
циональной дробью.
Если рациональная дробь
(
)
()
xQ
xP
n
m
является неправильной, в ней можно
выделить целую часть, т. е. преобразовать к виду
(
)
()
()
(
)
()
xQ
xR
xW
xQ
xP
n
m
n
m 1
+=
,
(4.6)
120
где
(
)
−
xW
многочлен - целая часть неправильной дроби;
(
)
()
−
xQ
xR
n
m
1
правильная
рациональная дробь:
nm
<
1
.
Любой многочлен с действительными коэффициентами
(
)
xQ
n
разлага-
ется единственным образом на произведение вещественных множителей сле-
дующего вида:
(
)
(
)
(
)
(
)
(
)
rs
lk
n
qpxxdcxxbxaxxQ ++⋅⋅++⋅−⋅⋅−⋅=
22
......α ,
(4.7)
где
−
α
вещественное число, равное коэффициенту при старшей степени
x
многочлена
(
)
xQ
n
,
−
ba ,..., вещественные корни многочлена кратности lk ,...,
соответственно, квадратные трёхчлены
(
)
(
)
qpxxdcxx ++++
22
,...,
не имеют
действительных корней (т. е.
...,,04
2
<− dc
)04
2
<− qp
, каждый из них соот-
ветствует паре комплексно сопряжённых корней многочлена
(
)
xQ
n
кратности
r
s
...,
,
соответственно, числа
lk,...,
,
−
r
s
...,
,
натуральные, причём
+
+
+
lk ... nrs
=
+
+
)...(2
.
Если дробь
(
)
()
−
xQ
xP
n
m
правильная, тогда с учётом (4.7 ) имеет место ра-
венство
(
)
() ( )
+
−
=
ax
A
xQ
xP
n
m
1
( )
++
−
...
2
2
ax
A
( )
++
−
...
k
k
ax
A
( )
+
−bx
B
1
( )
++
−
...
2
2
bx
B
( )
+
−
l
l
bx
B
( )
+
++
+
dcxx
DxC
2
11
( )
++
++
+
...
2
2
22
dcxx
Dx„
( )
С x D
x cx d
s s
s
+
+ +
+ +
2
...
( )
+
++
+
qpxx
NxM
2
11
( )
++
++
+
...
2
2
22
qpxx
NxM
( )
r
rr
qpxx
NxM
++
+
2
,
(4.8)
где ,,...,,,...,,,...,
2121 lk
BBBAAA
,,
11
DC
,...,,
22
DC
,...,,
ss
DC ,,
11
NM ,...,,
22
NM
−
rr
NM ,
некоторые действительные числа, коэффициенты разложения (4.8).
Дроби, входящие в правую часть равенства (4.8) называются про-
стейшими, а само равенство (4.8) называется разложением правильной ра-
циональной дроби на простейшие.
В частном случае, когда все
n
корней
n
aa ,...,
1
многочлена
(
)
xQ
n
явля-
ются разными действительными, тогда
(
)
(
)
(
)
nn
axaxxQ
−
⋅
⋅
−
⋅
=
...
1
α
и
(
)
() ( )
1
1
ax
A
xQ
xP
n
m
−
=
+
+
...
( )
n
n
ax
A
−
.
