Никифорова И.А. Математика в экономике: сборник задач. Часть ?
Подождите немного. Документ загружается.

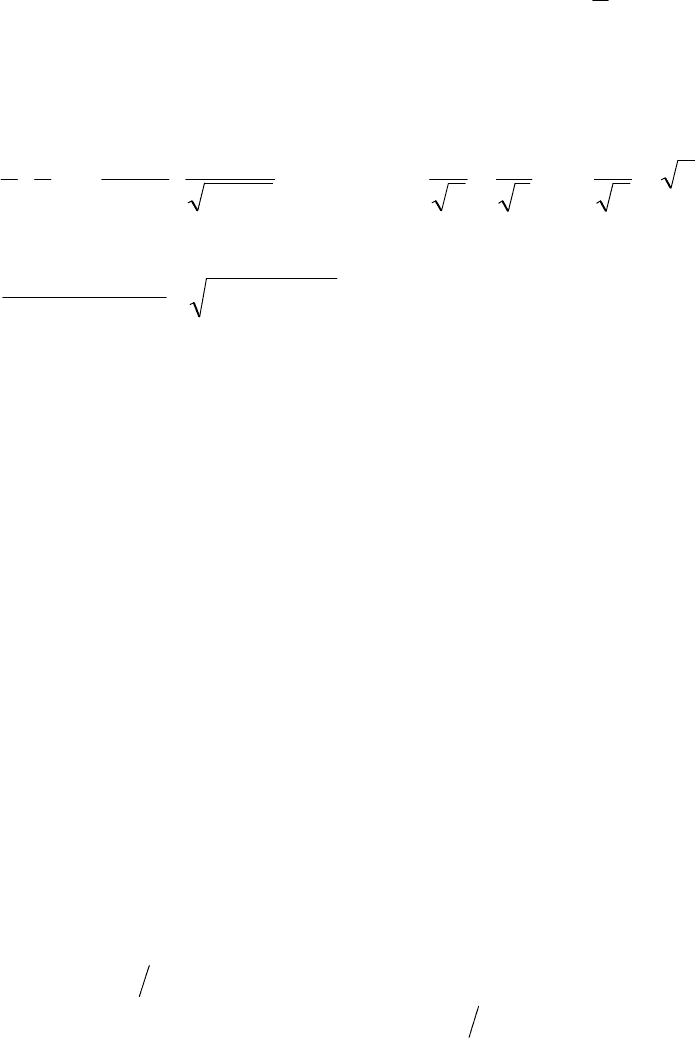
11
1. 3. Метод математической индукции
Метод используют для доказательства того, что некоторое утвержде-
ние выполняется для всех натуральных чисел. Суть метода состоит в сле-
дующем:
1) проверяется, что утверждение верно для единицы;
2) предполагается, что утверждение верно для произвольного на-
турального числа
1
−
n
;
3) доказывается, что утверждение верно для числа n.
1.23. Применяя метод математической индукции, доказать, что
N
n
∈
∀
справедливы равенства:
1)
( )
15,0...21 +⋅⋅=+++ nnn ;
2)
( )( )
121
6
1
...21
222
+⋅+⋅=+++ nnnn ;
3)
(
)
2
2333
125,0...21 +⋅⋅=+++ nnn .
1.24. Методом математической индукции доказать справедливость
неравенств:
1)
12
1
2
12
...
4
3
2
1
+
<
−
⋅⋅⋅
n
n
n
; 2)
( )
2
1
...
3
1
2
1
1 ≥>++++ nn
n
;
3)
(
)
n
n
nn 1
1
+>
+
при
3
≥
n
;
4)
n
n
n
xxx
n
xxx
⋅⋅⋅≥
+
+
+
...
...
21
21
при nkx
k
,...,1,0
=
≥
(среднее геометри-
ческое
n
неотрицательных чисел не превосходит их среднего арифмети-
ческого).
1.4. Бесконечно малые и бесконечно большие последовательности
Последовательность
{
}
n
α
называют бесконечно малой, если для лю-
бого сколь угодно малого числа
0
>
ε
найдётся номер
(
)
ε
NN
=
такой, что
для всех n >N выполнится неравенство
n
α
<ε. В этом случае пишут
0lim
=
∞→
n
n
x или
n
x → 0 при n→ ∞.
Последовательность
{
}
n
x называют бесконечно большой, если для
любого сколь угодно большого действительного числа
0
>
C
найдётся но-
мер
(
)
CNN
=
такой, что для всех n >N выполнится неравенство
n
x > C.
В этом случае пишут
∞
=
∞→
n
n
xlim или
n
x → ∞ при n→ ∞.
Сумма, разность, произведение бесконечно малых последовательно-
стей, а также произведение бесконечно малой последовательности на огра-
ниченную есть последовательность бесконечно малая.
Если последовательность
{
}
n
x
− бесконечно большая и 0
≠
n
x
N
n
∈
∀
, то
{
}
−
n
x1
бесконечно малая; если последовательность
{
}
n
α
−
бесконечно малая и 0
≠
n
α
N
n
∈
∀
, то
{
}
−
n
α
1
бесконечно большая.

12
Пример 1.1. Доказать, что
1) последовательность
{
}
a
n , где
0
≠
a
, произвольное действительное
число: при
0
>
a
является бесконечно большой, при
0
<
a
− бесконечно
малой;
2) последовательность
{
}
n
q при 1>q является бесконечно большой,
при 1<q − бесконечно малой.
Решение. 1) Пусть
0
>
a
. Из определения бесконечно большой по-
следовательности
{
}
n
x
для любого действительного числа
0
>
C
требует-
ся найти такой номер
(
)
СNN
=
, чтобы для всех n >N выполнялось нера-
венство
n
x > C . В рассматриваемом примере
a
n
nx = , выпишем нера-
венство
n
x > C: ⇒>Cn
a
Cn
a
> . Из обеих частей последнего нера-
венства извлечем корни степени
a
, поскольку
0
>
a
, то получим неравен-
ство
a
Cn > . Искомое число
(
)
СNN
=
определяется правилом:
[
]
{
}
a
CN ;1max= . Для записи номера
N
здесь используется функция
[
]
x ,
называемая целой частью числа
x
. По определению целая часть действи-
тельного числа
x
равна наибольшему целому числу, не превосходящему
x
. Итак, правило для определения числа N найдено, последовательность
{
}
a
n при
0
>
a
является бесконечно большой.
Пусть
0
<
a
. Из определения бесконечно малой последовательности
{
}
n
α
для любого действительного числа
0
>
C
требуется найти такой
номер
(
)
ε
NN
=
, чтобы для всех n >N выполнялось неравенство
n
α
<
ε
.
Имеем:
α
α n
n
= , выпишем неравенство
n
α
<
ε
: ⇒<ε
α
n ε
α
<n . Из
обеих частей последнего неравенства извлечем корни степени
α
, посколь-
ку
0
<
α
, то получим неравенство
α
ε>n . Искомое число
N
определяется
правилом:
[
]
{
}
α
ε;1max=N . Последовательность
{
}
α
n при
0
<
α
являет-
ся бесконечно малой.
2) Пусть 1>q . Докажем, что последовательность
{
}
n
q является бес-
конечно большой. Для любого действительного числа
0
>
C
выпишем не-
равенство
n
x > C при
n
n
qx = :
n
q > C Cq
n
>⇒ . Прологарифми-
руем обе части неравенства по основанию q , поскольку 1>q , получим
неравенство
>
n
q
qlog
⇒
C
q
log >⋅ qn
q
log
⇒
C
q
log
>
n
⇒
C
q
log

13
{
}
CN
q
log;1max
=
. Последовательность
{
}
n
q при 1>q является беско-
нечно большой.
При 1<q для любого
0
>
C
из неравенства
n
α
<
ε
при
n
n
q=α
получим:
n
q <
ε
ε<⇒
n
q . Прологарифмируем обе части неравенства
по основанию q , поскольку 1
<
q , получим неравенство
>
n
q
qlog
⇒
ε
q
log
>
n
⇒
ε
q
log
{
}
ε
q
N log;1max
=
.
Последовательность
{
}
n
q при 1<q является бесконечно малой.
1.25. Используя логическую символику, записать следующие выска-
зывания, а также их отрицания: 1) последовательность
{
}
n
α
является бес-
конечно малой; 2) последовательность
{
}
n
x является бесконечно большой.
1.26. Доказать, что заданные последовательности
{
}
n
x являются бес-
конечно малыми:
1)
(
)
n
x
n
n
1
1
+
−
= ;
2)
!
1
n
x
n
= ; 3)
1
2
3
+
=
n
n
x
n
;
4)
(
)
n
n
n
x 999,01 ⋅−= .
1.27. Доказать, что заданные последовательности
{
}
n
x являются бес-
конечно большими:
1) nx
n
−
=
; 2)
2
nx
n
= ; 3)
n
n
x 2= ;
4)
(
)
15
21
+⋅
⋅−
=
n
n
x
n
n
.
1.28. 1) Доказать, что любая бесконечно большая последователь-
ность является неограниченной.
2) Сформулировать и доказать основные свойства бесконечно боль-
ших последовательностей, связанные с арифметическими действиями над
последовательностями.
1.29. Доказать, что последовательности: 1)
(
)
(
)
{
}
n
n
⋅−+ 11 ;
2)
( )
{
}
n
n
1−
неограниченные, но не являются бесконечно большими.
1.30. Установить, какие из заданных последовательностей являются:
a) бесконечно малыми, б) бесконечно большими:
1)
(
)
n
n
nx 1−= ;
2)
n
x
n
100
= ; 3)
1
2
+
=
n
n
x
n
;
4)
2
sin
n
nx
n
π
= ;
5)
(
)
1
21
2
+
⋅−
=
n
n
x
n
n
;
6)
(
)
nx
n
lglg
=
.
1.5. Сходящиеся последовательности
Последовательность
{
}
n
x называют сходящейся к числу a, если для
любого числа
0
>
ε
найдётся номер
(
)
ε
NN
=
такой, что для всех n >N
выполнится неравенство ax
n
−
<ε. В этом случае пишут ax
n
n
=
∞→
lim или
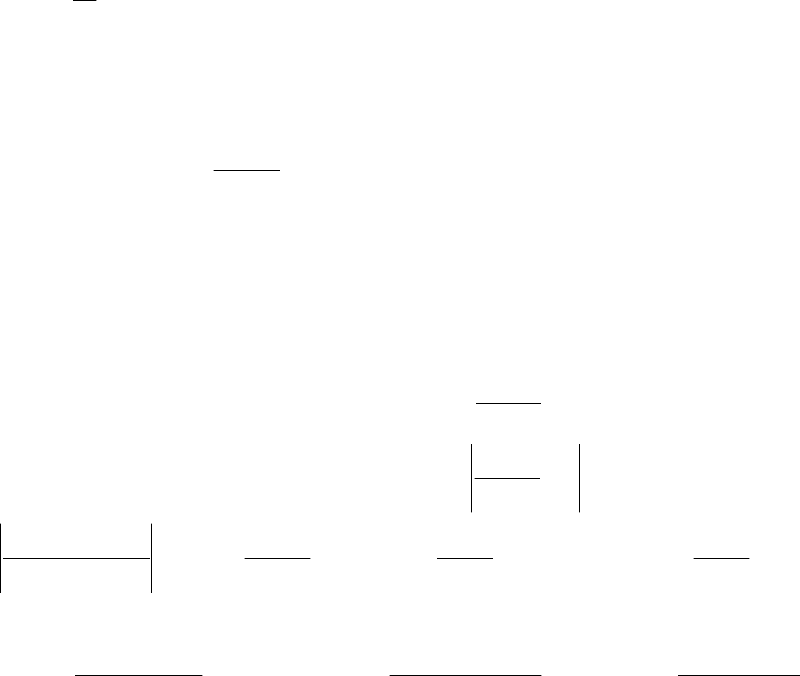
14
n
x → a при n→∞, число a называют пределом последовательности
{
}
n
x .
Последовательности, не являющиеся сходящимися, называют расходящи-
мися.
Если с − постоянная, ax
n
n
=
∞→
lim , by
n
n
=
∞→
lim , тогда
1) сс
n
=
∞→
lim ; 2)
(
)
=
±
∞→
nn
n
yxlim
±
∞→
n
n
xlim bay
n
n
±
=
∞→
lim ;
3)
(
)
=
⋅
∞→
nn
n
yxlim
b
a
⋅
; 4)
(
)
=
⋅
∞→
n
n
xсlim
a
с
⋅
;
5)
(
)
=
∞→
nn
n
yx /lim
b
a
/
,
0
≠
b
.
Если
n
x → a,
n
y → b при n→∞ и, начиная с некоторого номера,
⇒
≤
nn
yx
b
a
≤
.
Пусть даны три последовательности:
{
}
n
x ,
{
}
n
y ,
{
}
n
z . Если, начиная
с некоторого номера,
nnn
zyx
≤
≤
и
n
x → a,
n
z → a при n→∞, тогда
n
y → a
при n→∞.
Данные свойства широко используются при вычислении пределов. В
тех случаях, когда свойства пределов непосредственно применить не уда-
ётся, например, когда общий член последовательности представим в виде
отношения двух бесконечно больших последовательностей (неопределён-
ность
∞
∞
) или разности двух бесконечно больших последовательностей од-
ного знака (неопределённость
∞
−
∞
) и т.д., общий член последовательно-
сти следует предварительно преобразовать.
Пример 1.2. Пользуясь определением предела последовательности
доказать, что 5
1
2
10
lim =
−
∞→
n
n
n
.
Решение. Из определения предела последовательности видно: для
доказательства существования предела ax
n
n
=
∞→
lim следует
∀
0
>
ε
найти
такой номер
(
)
ε
NN
=
, чтобы для всех n >N выполнялось неравенство
ax
n
−
<ε.
В рассматриваемом примере
1
2
10
−
=
n
n
x
n
,
5
=
a
. Выпишем
∀
0
>
ε
не-
равенство ax
n
−
<ε, получим ε<−
−
5
12
10
n
n
. Преобразуем его:
⇒<
−
+−
ε
12
51010
n
nn
⇒<
−
ε
1
2
5
n
⇒
+
>
ε
ε
2
5
n
+
=
ε
ε
2
5
;1maxN .
Пример 1.3. Вычислить:
1)
7
3
54
lim
2
2
−
+
++
∞→
n
n
nn
n
; 2)
7
5
3
142
lim
23
2
−
+
−+
∞→
n
n
nn
n
; 3)
3
12
lim
3
4
+
+
++
∞→
n
n
nn
n
;

15
4)
(
)
( )
!!1
!2
lim
nn
n
n
++
+
∞→
;
5)
5
7
7
lim
1
+
+
∞→
n
n
n
;
6)
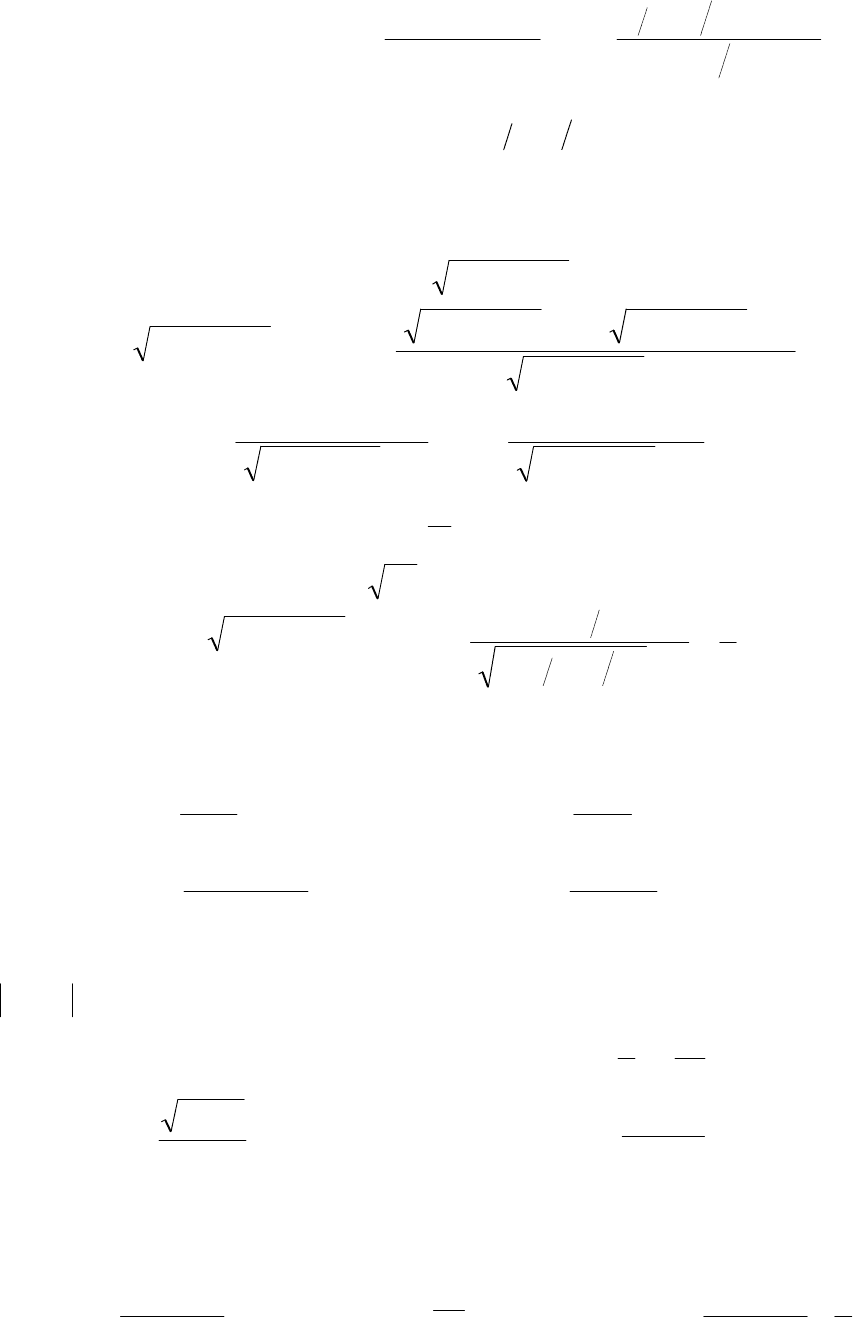
(
)
1
cos32
lim
2
+
⋅
−
∞→
n
nn
n
;
7)
(
)
nnn
n
−++
∞→
13lim
2
.
Решение. 1) Имеем неопределённость
∞
∞
. Разделим числитель и зна-
менатель на
2
n
(старшую степень
n
в примере):
=
−
+
++
∞→
7
3
54
lim
2
2
n
n
nn
n
=
−+
++
∞→
2
2
713
541
lim
nn
nn
n
(
)
( )
=
−+
++
∞→
∞→
2
2
713lim
541lim
nn
nn
n
n
=
−+
++
∞→∞→∞→
∞→∞→∞→
2
2
7lim1lim3lim
5lim4lim1lim
nn
nn
nnn
nnn
=
−+
+
+
0
0
3
001
3
1
.
2) Имеем неопределённость
∞
∞
. Разделим числитель и знаменатель
на
3
n
:
=
−
+
−+
∞→
7
5
3
142
lim
23
2
n
n
nn
n
=
−+
−+
∞→
3
32
753
142
lim
nn
nnn
n
0
0
0
3
000
=
−+
−
+
.
3) Имеем неопределённость
∞
∞
. Разделим числитель и знаменатель
на
4
n
:
=
+
+
++
∞→
3
12
lim
3
4
n
n
nn
n
∞=
++
++
∞→
43
43
311
112
lim
nnn
nn
n
,
поскольку числитель дроби стремится к числу, равному 2, а знаменатель
является бесконечно малым при
∞
→
n
.
4) Имеем неопределённость
∞
∞
. Напомним, что использованная в
примере функция факториал
(
)
!nnf
=
определена на множестве всех неот-
рицательных целых чисел, причём:
(
)
10
=
f ,
(
)
⋅
=
nnf
(
)
Nnnf
∈
∀
−
1 .
Следовательно,
n
n
⋅
⋅
⋅
=
...
2
1
!
,
(
)
(
)
1!!1
+
⋅
=
+
nnn ,
(
)
(
)
(
)
21!!2
+
⋅
+
⋅
=
+
nnnn . С
учётом этого:
(
)
( )
=
++
+
∞→
!!1
!2
lim
nn
n
n
(
)
(
)
( )
=
⋅++
⋅
+
⋅
+
∞→
!11
!12
lim
nn
nnn
n
(
)
(
)
( )
=
+
+
⋅
+
∞→
2
12
lim
n
nn
n
(
)
∞
=
+
∞→
1lim n
n
.
5) Имеем неопределённость
∞
∞
. Разделим числитель и знаменатель
на
n
7
: =
+
+
∞→
5
7
7
lim
1
n
n
n
7
751
7
lim =
+
∞→
n
n
.
6) Последовательности, стоящие в числителе и знаменателе рассмат-
риваемой в примере дроби, не имеют конечных пределов при
∞
→
n
. Раз-
16
делим числитель и знаменатель дроби на старшую степень
n
, имеющуюся
в примере: на
2
n
. Получим:
(
)
=
+
⋅
−
∞→
1
cos32
lim
2
n
nn
n
(
)
0
11
cos32
lim
2
2
=
+
⋅−
∞→
n
nnn
n
,
поскольку преобразованный числитель равен произведению бесконечно
малой при
∞
→
n
последовательности
(
)
2
32 nn − и ограниченной после-
довательности
n
cos
, следовательно, является бесконечно малым при
∞
→
n
, а знаменатель стремится к 1 при
∞
→
n
.
7) Имеем неопределённость
∞
−
∞
. Умножим и разделим общий
член последовательности на сумму
(
)
nnn +++ 13
2
:
(
)
=−++
∞→
nnn
n
13lim
2
(
)
(
)
(
)
=
+++
+++⋅−++
∞→
nnn
nnnnnn
n
13
1313
lim
2
22
(
)
=
+++
−++
∞→
nnn
nnn
n
13
13
lim
2
22
(
)
nnn
n
n
+++
+
∞→
13
13
lim
2
.
Получили неопределённость
∞
∞
. Разделим числитель и знаменатель
дроби на старшую степень
2
nn = :
(
)
=−++
∞→
nnn
n
13lim
2
(
)
2
3
1131
13
lim
2
=
+++
+
∞→
nn
n
n
.
1.31. Пользуясь определением предела последовательности, доказать
равенства:
1) 2
3
2
lim =
+
∞→
n
n
n
; 2) 0
cos
lim =
∞→
n
n
n
;
3) 1
3
53
lim
2
2
=
+
+−
∞→
n
nn
n
; 4) 3
3
53
lim
1
=
−
+
∞→
n
n
n
.
1.32. Найти
n
n
xa
∞→
=
lim и определить номер
(
)
ε
N такой, что
ε<−ax
n
при всех
(
)
ε
Nn
>
, если:
1) ;001,0,3...33,0
=
=
ε
321
n
n
x
2) ;001,0,
2
sin
1
== ε
π
n
n
x
n
3) ;005,0,
1
2
=
+
= ε
n
n
x
n
4) .005,0,
3
5
1
2
2
=
−
+
= ε
n
n
x
n
1.33. Доказать, что заданные последовательности - расходящиеся.
Определить, являются ли последовательности ограниченными или неогра-
ниченными:
1)
(
)
( )
n
n
n
x
12
12
−−
−+
= ;
2)
4
cos
n
x
n
π
= ;
3)
(
)
n
x
n
n
1
2
12
−
−+
= ;

17
4)
(
)
0>= knx
k
n
; 5)
(
)
(
)
121 +−= nx
n
n
;
6)
3
sin
2
2 n
n
n
x
n
π
−
+
= .
Вычислить пределы:
1.34.
n
n
n
3
1
lim
−
∞→
.
1.35.
n
nn
n
5
2
173
lim
2
−
+−
∞→
.
1.36.
1
32
lim
2
+
−
∞→
n
n
n
.
1.37.
( )
3
3
1
2
lim
+
∞→
n
n
n
.
1.38.
(
)
(
)
n
n
nn
n
39
95
22
lim
3
33
+
−−+
∞→
.
1.39.
+
+
−
+
−
∞→
3
3
52
21
75
12
lim
n
n
n
n
n
.
1.40.
1
2
2
lim
1
+
+
∞→
n
n
n
. 1.41.
2
3
35
lim
−
⋅
∞→
n
n
n
.
1.42.
nn
nn
n
2
3
3
5
32
lim
⋅
−
⋅
+
∞→
.
1.43.
1
lim
2
+
∞→
n
n
n
.
1.44.
1
23
lim
2
3
4
+
++
∞→
n
nn
n
.
1.45.
5
11
lim
4
3
2
+
+++
∞→
n
nn
n
.
1.46.
5116
319
lim
4
4
3
32
++⋅
+++
∞→
n
nn
n
.
1.47.
( )
(
)
( )
( )( )
121
59213
lim
3
2
3
3
2
2
++−
+−+
∞→
nnn
nnn
n
1.48.
3
2
2
724
23
lim
++
−+
∞→
nn
nn
n
.
1.49.
( )
!!1
!
lim
nn
n
n
−+
∞→
.
1.50.
(
)
(
)
( )
!!1
!2!1
lim
nn
nn
n
−+
+
−
+
∞→
. 1.51.
4
cos
1
3
lim
n
n
n
n
π
⋅
+
⋅
∞→
.
1.52.
1
sin
lim
2
+
⋅
∞→
n
nn
n
.
1.53.
+
+
∞→
n
n
n
n
n
10
!cos
115
lim .
1.54.
n
n
nn
n
−
−
∞→
2
lim .
1.55.
(
)
13lim −−+
∞→
nn
n
.
1.56.
(
)
132lim −−+
∞→
nn
n
.
1.57.
(
)
1lim
22
+−
∞→
nnn
n
.
1.58.
(
)
11lim
22
+−−−+
∞→
nnnn
n
.
1.59.
(
)
21lim
332/3
−−+
∞→
nnn
n
.
1.60.
(
)
3
3
3
3
52lim +−+
∞→
nn
n
.
1.61.
(
)
nnn
n
+−
∞→
3
32
lim .
1.62.
−
−
+
∞→
13
3
1
lim
2
2
3
n
n
n
n
n
.
1.63.
(
)
1
sin
lim
2
3
2
−
⋅
∞→
n
nn
n
.
1.64.
−
+++
∞→
222
1
...
21
lim
n
n
nn
n
.
1.65.
(
)
−
+
−++++
∞→
n
n
n
n
2
1
34...951
lim .
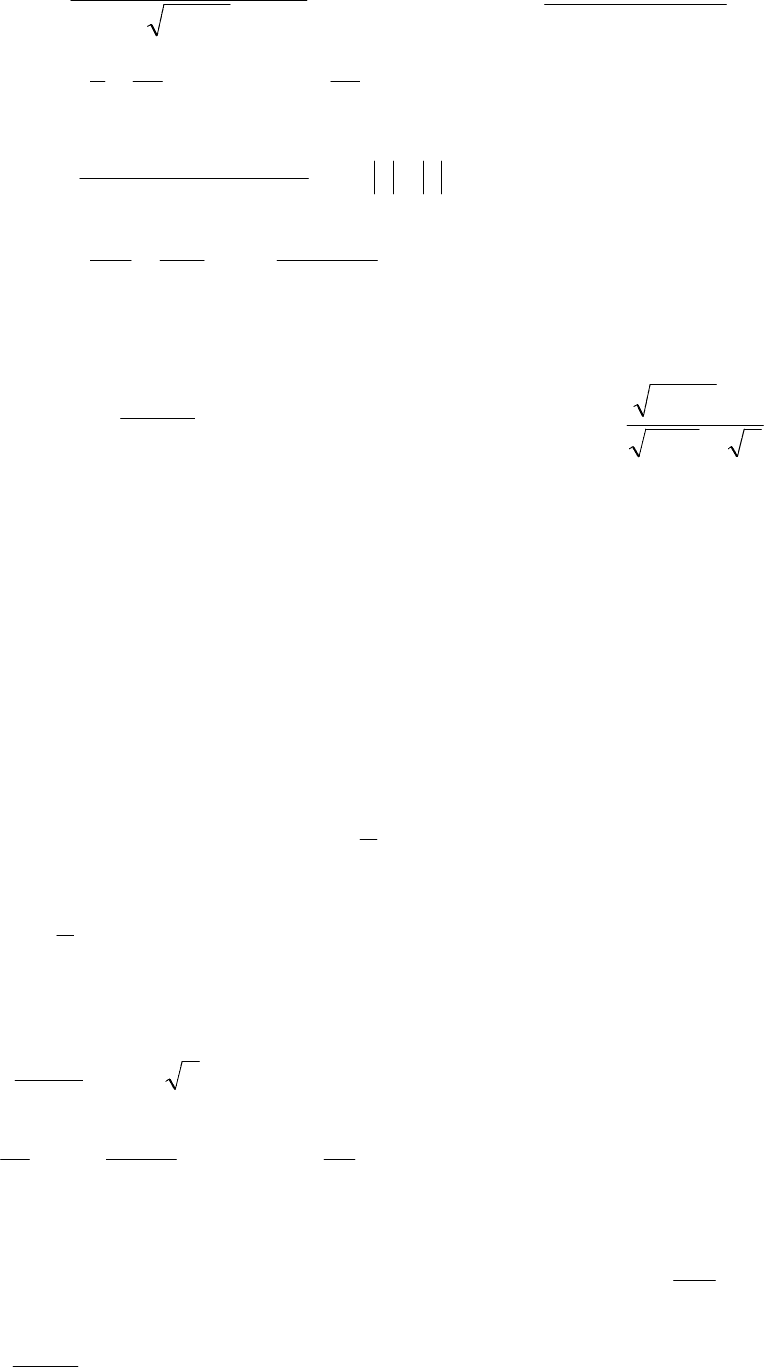
18
1.66.
1
4...8642
lim
2
+
−
+
−
+
−
∞→
n
n
n
.
1.67.
3
222
...21
lim
n
n
n
+++
∞→
.
1.68.
( )
⋅−++−
−
∞→
n
n
n
5
1
1...
25
1
5
1
lim
1
.
1.69.
12
12
...1
...1
lim
−
−
∞→
++++
++++
n
n
n
bbb
aaa
, 1>> ba .
1.70.
( )
+⋅
++
⋅
+
⋅
∞→
1
1
...
32
1
21
1
lim
nn
n
.
1.71. Исследовать последовательность
{
}
n
x на сходимость в зависи-
мости от значений параметров
γ
β
α
,
,
, если:
1)
3
1
+
+
=
β
α
n
n
x
n
;
2)
nn
nn
nx
n
−+
−+
⋅=
1
1
3
3
γ
.
1.6. Монотонные последовательности. Число
e
Последовательность
{
}
n
x называют возрастающей, если
nn
xx
>
+1
для всех n
N
∈
, неубывающей, если
nn
xx
≥
+1
для всех n
N
∈
, убывающей,
если
nn
xx
<
+1
для всех n
N
∈
, невозрастающей, если
nn
xx
≤
+1
для всех
n
N
∈
. Все эти последовательности называют монотонными.
Монотонные ограниченные последовательности являются сходящи-
мися.
Последовательность
+
n
n
1
1
− возрастающая ограниченная,
e
n
n
n
=
+
∞→
1
1lim , где e − число, e ≈ 2,7.
1.72. Доказать, что последовательности:
1)
+12n
n
, 2)
{
}
n , 3)
{
}
2
n − монотонно возрастающие;
4)
n
n
5
, 5)
−34n
n
, 6)
+
n
2
1
1 −монотонно убывающие.
1.73. Выяснить, монотонна ли последовательность
{
}
n
x и есть ли у
неё наибольший и наименьший элементы, если: 1)
!
10
n
n
; 2)
{
}
n
2 ;
3)
+
n
n
3
13
.
19
1.74. Доказать существование пределов последовательностей:
1)
+
++
+
+
+
+
+ 12
1
...
12
1
12
1
12
1
32 n
;
2)
+
++
+
+
+
+
+ n
n
3
1
...
33
1
23
1
13
1
32
;
3)
++
⋅⋅
+
⋅
+
!
1
...
432
1
32
1
2
1
n
; 4)
++++
222
1
...
3
1
2
1
1
n
.
1.75. Доказать, что последовательность
{
}
n
x сходится, и найти её
предел, если: 1)
!
2
n
x
n
n
= ; 2)
n
n
n
n
x
!
= .
1.76. Доказать сходимость и вычислить предел последовательности
{
}
n
x , если она задана рекуррентным соотношением:
1) 3
1
=x ,
nn
xx +=
+
3
1
; 2) 2
1
=x ,
nn
xx ⋅=
+
2
1
;
3) 3
1
=
x ,
+=
+
n
nn
x
xx
3
2
1
1
.
1.77. Доказать, что неограниченная монотонная последовательность
является бесконечно большой.
1.78. Найти пределы:
1)
1
1
1lim
+
∞→
+
n
n
n
; 2)
n
n
n
+
∞→
3
1
1lim ; 3)
n
n
n
n
−
∞→
1
lim .
1.7. Числовые последовательности в экономике
1. Простые и сложные проценты. На финансовом рынке кредитор
получает доход от предоставления денег в долг в любой форме: выдачи
ссуды, помещения денег на сберегательный счёт, покупки акций, облига-
ций и т.д. Получаемый доход называют процентными деньгами (или про-
сто процентами). Предоставление денег в долг как правило связано с од-
ной из двух операций - наращения или дисконтирования денежной сум-
мы.
Пусть P − первоначальная величина долга,
−
%
i
кредитная (про-
центная) ставка, под которую одалживаются деньги. По истечении каждо-
го из равных, заранее оговорённых, периодов времени долг увеличивается.
Обозначим через
n
S наращённую сумму долга по истечении
n
периодов
после предоставления денег в долг.
Множество наращённых сумм долга образует соответствующую по-
следовательность
{
}
n
S .
Кроме перечисленных выше величин наращённая сумма
n
S зависит
от способа начисления процентов (вида процентных ставок). Существует
два основных способа начисления процентов.

20
В случае простой процентной ставки в конце любого периода сумма
долга увеличивается на величину i⋅P, i − доля единицы, соответствующая
%
i
(процентная ставка применяется к первоначальной сумме долга), тогда
(
)
...,1,0,1
=
⋅
+
⋅
=
ninPS
n
.
В случае сложной процентной ставки в конце любого периода сумма
долга увеличивается на величину i⋅
1−n
S , (процентная ставка применяется
ко всей имеющейся к данному моменту времени сумме долга, с учётом ра-
нее начисленных процентов), тогда
(
)
...,1,0,1 =+⋅= niPS
n
n
.
Процентная ставка i равна отношению дохода за один первый пери-
од к сумме вложенных средств: i =
P
PS
−
1
Годовая процентная ставка i
(m)
называется номинальной, если для на-
числения сложных процентов за
m
1
часть года применяется ставка
m
i
m)(
.
Таким образом, если сложные проценты начисляются через равные
промежутки времени m раз в году, то в конце каждого периода длиной
m
1
проценты начисляются по ставке
m
i
m)(
. Если срок долга n лет, то mn -
число периодов применения ставки
m
i
m)(
в сроке долга. Из формулы для
наращенной суммы в случае сложных процентов получаем
mn
m
n
m
i
PS
+=
)(
1 .
Начисление процентов при неограниченном уменьшении длины пе-
риодов времени начисления процентов (т.е. за бесконечно малые периоды
времени) называют непрерывным. При непрерывном начислении сложных
процентов годовую номинальную процентную ставку обозначают через δ и
называют силой роста или интенсивностью процентов, а также непрерыв-
ной процентной ставкой. Формула для наращенной суммы в этом случае
S
n
= P
e
n δ
.
Процентные ставки различного вида, приводящие к одному и тому
же финансовому результату за один и тот же срок, называют эквивалент-
ными.
Операция дисконтирования применяется тогда, когда задана сумма
погашаемого долга S
n
, которую следует уплатить по истечении
n
перио-
дов после предоставления денег в долг, при этом требуется найти сумму
первоначального долга P. В этом случае говорят, что сумма S
n
дисконти-
руется или учитывается.
