Никифорова И.А. Математика в экономике: сборник задач. Часть ?
Подождите немного. Документ загружается.


51
()
axa
xa
xa
xa
axa
x
y
xy
xxx
sin
2
2
sin
lim
2
sinlimlim
000
−=
∆⋅
∆
⋅
⋅
∆⋅
+−=
∆
∆
=
′
→∆→∆→∆
.
Следовательно, axay sin
−
=
′
.
Пример 3.2. Для функции
()
>+−
≤
=
1,2
1,
2
xxx
xx
xf найти односто-
ронние производные
(
)
1
−
′
f и
(
)
1
+
′
f . Определить, имеет ли функция в точ-
ке
1
=
x
производную.
Решение. При
1
≤
x
функция определяется формулой
(
)
xxf
=
, по-
этому
()
(
)
(
)
1
11
lim
11
lim1
00
=
∆
−
∆
+
=
∆
−
∆
+
=
′
−→∆−→∆
−
x
x
x
fxf
f
xx
.
При
1
>
x
функция
(
)
xxxf 2
2
+−= , следовательно,
()
(
)
(
)
(
)
(
)
=
∆
−∆++∆+−
=
∆
−∆+
=
′
+→∆+→∆
+
x
xx
x
fxf
f
xx
1121
lim
11
lim1
2
00
(
)
0lim
12221
lim
0
2
0
=∆−=
∆
−∆++∆−∆−−
+→∆+→∆
x
x
xxx
xx
.
Итак,
(
)
11
=
′
+
f ,
(
)
.01
=
′
−
f Поскольку
(
)
(
)
11
−+
′
≠
′
ff , то производ-
ная
(
)
1f
′
не существует.
3.1. Пользуясь определением производной, найти производные
следующих функций:
1)
3
xy = ; 2) xy = ;
3)
x
y
3
sin
=
;
4)
1−
= xy ;
5) xy
2
log
=
;
6)
3
2
xy = .
3.2. Дать интерпретацию отношению
(
)
(
)
(
)
x
xfxxf
x
xf
∆
−
∆
+
=
∆
∆
и
производной
()
(
)
x
xf
xf
x
∆
∆
=
′
→∆ 0
lim в следующих случаях:
1) материальная точка М движется прямолинейно в заданном на-
правлении по закону
(
)
tfs
=
, где
−
=
t
x
момент времени, а
−
s
путь, прой-
денный материальной точкой за время
t
,
0
≥
t
;
2) фирма производит продукцию одного вида, производственная
функция
(
)
tfQ
=
определяет зависимость объёма выпущенной продукции
Q
от времени работы фирмы
t
x
=
,
0
≥
t
;
3) рассматривается рынок одного товара, для которого известна
(
)
−
=
PfS функция предложения
S
от цены товара
P
x
=
.
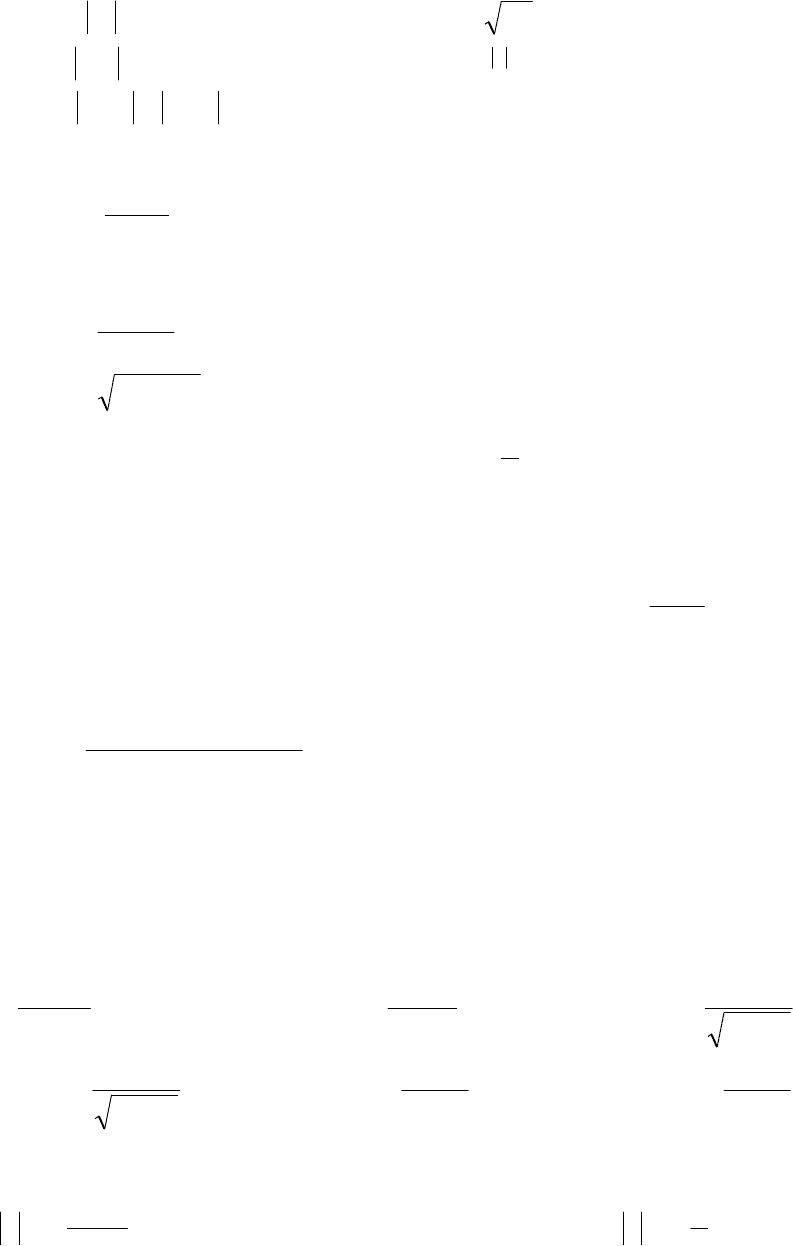
52
3.3. Найти односторонние производные функций в указанных точ-
ках. Определить, имеют ли функции в этих точках а) производные; б)
бесконечные производные:
1)
(
)
13 += xxf вточке
0
=
x
;
2)
()
5
2
xxf = в точке
0
=
x
;
3)
(
)
xxf ln= в точке
1
=
x
;
4)
(
)
x
xf 2= в точке
0
=
x
;
5)
(
)
11 ++−= xxxf в точках
1
±
=
x
;
6)
()
>
−
≤−
=
1,
2
1
,1,
2
23
x
x
xxx
xf
в точке
1
=
x
;
7)
()
≠
+
=
=
0,
1
,0,0
/1
x
e
x
x
xf
x
в точке
0
=
x
;
8*)
()
2
1
x
exf
−
−= в точке
0
=
x
.
3.4. Показать, что функция
()
>
≠
=
1,0
0,
1
sin
x
x
x
x
xf непрерывна в
точке
0
=
x
, но не имеет в этой точке ни левой, ни правой производных.
3.5. Известно, что
(
)
00
=
f и существует предел
(
)
x
xf
x 0
lim
→
. Дока-
зать, что этот предел равен
(
)
0f
′
.
3.6. Доказать, что если функция
(
)
xf имеет производную в точ-
ке
0
x , то
(
)
(
)
( ) ( )
000
0
00
0
lim xfxxf
xx
xfxxfx
xx
′
⋅−=
−
⋅
−
⋅
→
.
3.2. Производная явной функции
1. Таблица производных основных элементарных функций.
1.
(
)
,0,
1
≠⋅=
′
−
αα
αα
xx 2 .
( )
xx cossin =
′
.
−
a
действительное число.
3.
( )
xx sincos −=
′
.
4.
( )
x
tgx
2
cos
1
=
′
. 5.
( )
x
ctgx
2
sin
1
−=
′
.
6.
( )
2
1
1
arcsin
x
x
−
=
′
.
7.
( )
2
1
1
arccos
x
x
−
−=
′
.
8.
( )
2
1
1
x
arctgx
+
=
′
.
9.
( )
2
1
1
x
arcctgx
+
−=
′
.
10.
(
)
−>=
′
aaaaa
xx
,0,ln действительное число. 11.
(
)
xx
ee =
′
.
12.
( )
1,0,
ln
1
log ≠>=
′
aa
a
x
x
a
,
−
a
действительное число.
13.
( )
x
x
1
ln =
′
.
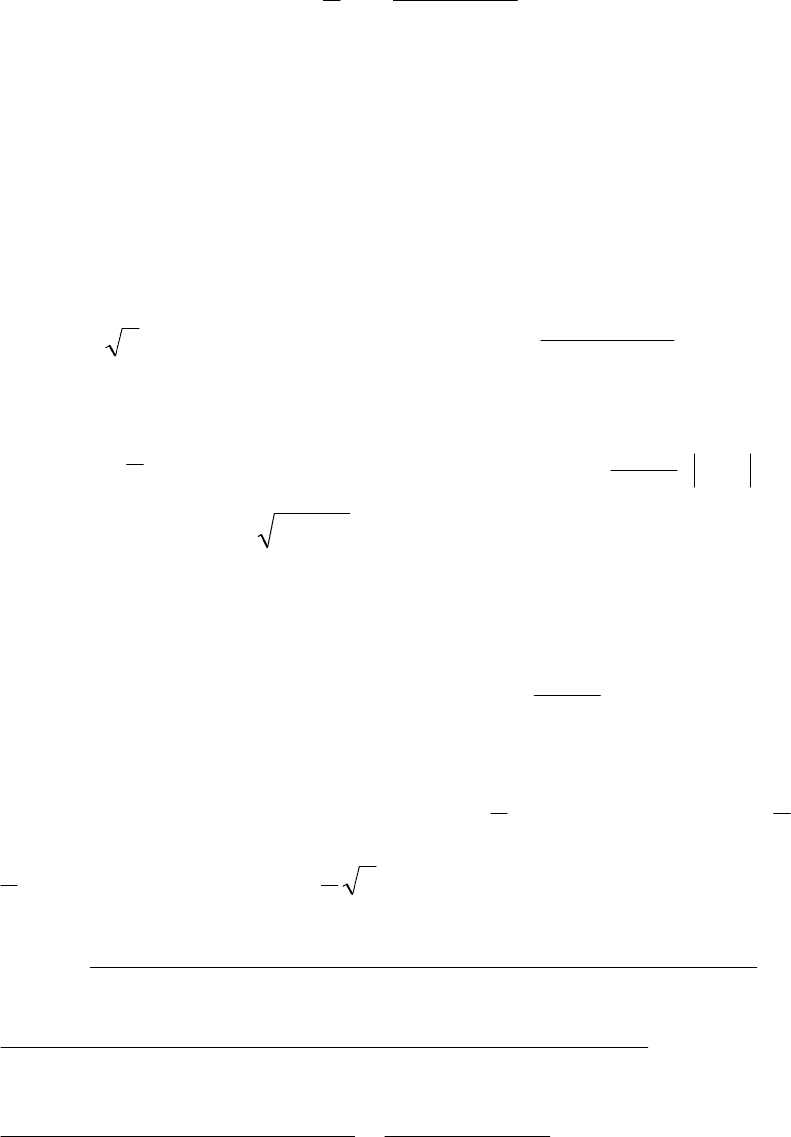
53
2. Основные правила дифференцирования. Пусть
−
c
постоянная
величина и функции
(
)
xuu
=
и
(
)
xvv
=
дифференцируемы, тогда
1.
()
.0=
′
с . 2.
( )
uccu
′
⋅=
′
. 3.
( )
vuvu
′
±
′
=
′
± .
4.
( )
vuvuvu
′
⋅+⋅
′
=
′
⋅ .
5. 0,
2
≠
′
⋅−⋅
′
=
′
v
v
vuvu
v
u
.
6. Если функция
(
)
xuu
=
дифференцируема в точке
0
x , функция
(
)
ufy
=
дифференцируема в точке
(
)
00
xuu
=
, то сложная функция
(
)
(
)
xufy
=
дифференцируема в точке
0
x и
(
)
(
)
(
)
(
)
000
xuxufxy
ux
′
⋅
′
=
′
. (3.1)
Пример 3.3. Применяя таблицу производных и правила дифферен-
цирования, найти производные следующих функций:
1) 4752
23
++−= xxxy ; 2) arctgxxy ⋅=
3
;
3)
(
)
2ln3 −⋅= xxxy ;
4)
x
x
xx
y
cos
sin
cossin
+
−
= ;
5)
(
)
4
5
32 += xy ;
6)
(
)
52sin
+
=
xy ;
7)
2
ln
x
tgy = ;
8) 1,
1
2
arcsin
4
2
<
+
= x
x
x
y ;
9)
xxx
eearctgey
2
1ln +−⋅= .
Решение. 1)
(
)
(
)
( ) ()
(
)
(
)
()
=+
′
+
′
−
′
=
′
+
′
+
′
−
′
=
′
07524752
2323
xxxxxxy
7
10
6
1
7
2
5
3
2
22
+
−
=
⋅
+
⋅
−
⋅
=
x
x
x
x
.
2)
(
)
( )
2
3
233
1
3
x
x
arctgxxarctgxxarctgxxy
+
+=
′
+
′
=
′
.
3) Перепишем функцию в следующем виде
(
)
2ln3
2/3
−⋅= xxy , тогда
(
)
( ) ( )
=
′
−⋅+−⋅
′
=
′
2ln32ln3
2/32/3
xxxxy
( )
=⋅+−⋅
x
xxx
3
2ln3
2
3
2/32/1
xxxxxx ln
2
9
33ln
2
9
2/12/12/1
=+−⋅ .
4)
( ) ( ) ( )( )
( )
=
+
′
+⋅−−+⋅
′
−
=
′
2
cossin
cossincossincossincossin
xx
xxxxxxxx
y
(
)
(
)
(
)
(
)
( )
=
+
−
⋅
−
−
+
⋅
+
2
cossin
sincoscossincossinsincos
xx
xxxxxxxx
(
)
(
)
( ) ( )
22
22
cossin
2
cossin
cossincossin
xxxx
xxxx
+
=
+
−++
.
5) Применим формулу (3.1) производной сложной функции, учиты-
вая, что промежуточный аргумент
(
)
32
5
+= xu , а
(
)
4
uuf = . Вычислим

54
() ()
(
)
453
1032,4 xxxuuuf =
′
+=
′
=
′
,
подставляя в формулу (3.1), получим
()
(
)
(
)
3
544
3
5
324010324 +⋅=⋅+=
′
=
′
xxxxxyy
x
.
6)
( )( ) ( )
52cos25252cos +=
′
+⋅+=
′
xxxy .
7) При нахождении производной здесь последовательно дважды ис-
пользуется формула производной сложной функции:
xco
x
xx
x
xx
tg
x
tg
x
tg
y sec
sin
1
2
cos
2
sin2
1
2
2
cos
1
2
1
2
2
1
2
==
⋅
=
′
⋅⋅=
′
⋅=
′
.
8) =
′
+
⋅
+
−
=
′
4
2
2
4
2
1
2
1
2
1
1
x
x
x
x
y
(
)
( )( )
(
)
(
)
=
+
⋅−+⋅
⋅
+−++
+
2
4
234
4242
4
1
2414
2121
1
x
xxxx
xxxx
x
.
( )
(
)
( ) ( )
44
4
4
1
4
1
14
1
1
x
x
x
xx
x +
=
+
−⋅
⋅
−
=
.
9) Используя свойства логарифма, перепишем исходную функцию в
виде
(
)
xxx
eearctgey
2
1ln
2
1
+−⋅= и вычислим производную
( )
( )
2
22
2
2
111
()(ln1)2
22
1
1
.
x
xxxxxx
x
x
xx
e
yearctgeeearctgee
e
e
earctge
′′′
=⋅−+=⋅+−⋅⋅=
+
+
=⋅
Пример 3.4. Вычислить
(
)
0
xf
′
, если
1)
()
;8,
16
1
0
3
2
=+−= x
x
xxf 2)
(
)
(
)
2,2cos
0
2
=−⋅= xxxxf .
Решение. При решении данных примеров следует сначала найти про-
изводные
(
)
xf
′
, а затем вычислить их значения в точках
0
x :
1)
()
;
16
3
2
2
3
1
x
xxf −−=
′
−
()
12
7
4
1
3
1
8
16
83
2
8
23
−=−−=−−=
′
f ;
2)
(
)
(
)
(
)
;2sin2cos2
2
−−−=
′
xxxxxf
(
)
40sin20cos222
2
=−⋅=
′
f .
3.7. Найти производные функций:
1) 54
3
2
3
−+−= xx
x
y ;
2)
7
53
+
=
x
y ;
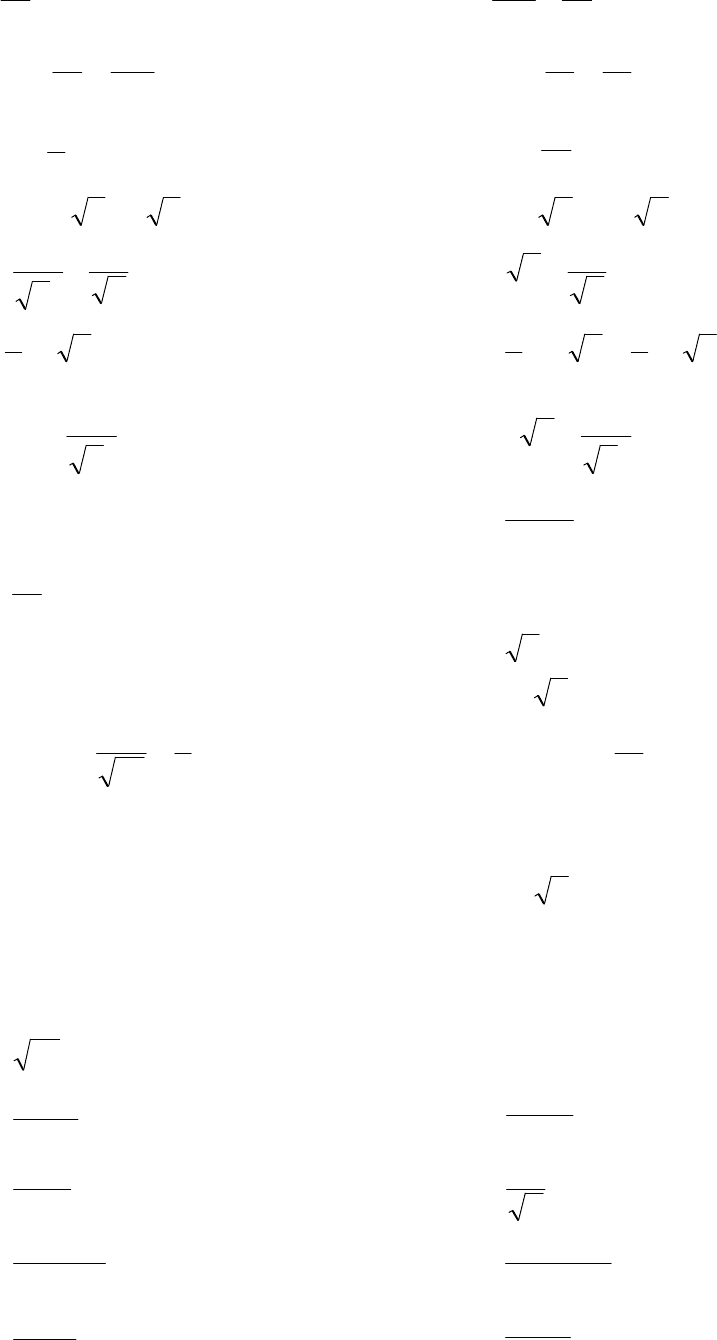
55
3)
3
7
x
y = ; 4)
23
6
4
1
x
x
y −= ;
5)
42
4
12
3
x
x
xy +−= ; 6)
5
2
11
x
x
xy −+= ;
7)
2
2
1
−=
x
y ;
8)
2
2
3
1
+=
x
y ;
9)
3
32 xxxy −⋅+= ; 10)
43
46 xxy ⋅−⋅= ;
11)
x
x
y
23
3
−= ;
12)
2
6
3
++=
x
xy
;
13)
3
4
3
xxy ⋅= ; 14)
4
3
5
4
7
2
xxxxy ⋅+⋅= ;
15)
2
4
1
−=
x
xy ; 16)
3
3
3
1
+=
x
xy ;
17)
x
x
x
y
cos
6
sin
2
−
+
=
;
18) 45
3
cos
+⋅+= tgx
x
y ;
19) 73
2
2
−⋅+= tgx
x
y ;
20)
x
ctgx
y
sin
4
+
=
;
21)
x
exy ⋅−= 4sin5 ;
22)
x
exy ⋅+= 7
5
;
23)
x
xy 53
2
⋅+= ;
24) 528
4
+−⋅=
x
xy ;
25)
2
12
ln2
3
2
−+=
x
xy
;
26)
x
xxy
3
ln ++= ;
27)
3
2
+
−
=
arctgx
x
y
; 28)
x
x
y
arcsin
5
sin
+
=
;
29) xxy cos
3
⋅= ;
30)
(
)
ctgxxy
⋅
+
=
1 ;
31)
(
)
xxxxy cos2sin2
2
+⋅−= ; 32) xxy sin2 ⋅⋅= ;
33)
x
exy ⋅=
2
;
34)
(
)
1
3
−⋅=
x
exy ;
35)
(
)
1sin2 +⋅= xy
x
; 36) xey
x
arcsin⋅= ;
37)
(
)
arctgxey
x
⋅−= 5 ; 38)
(
)
xxey
x
cossin3 −−⋅= ;
39) xxy ln
3
2
⋅= ;
40)
(
)
xxxy
3
3
log2 ⋅−= ;
41)
1
2
2
+
=
x
x
y ;
42)
x
x
y
4
1
−
= ;
43)
2
cos
x
x
y = ;
44)
x
tgx
y =
;
45)
x
x
y
cos
1
sin2
+
⋅
= ; 46)
x
x
y
sin
2
1
cos
+
= ;
47)
x
x
e
e
y
−
+
=
1
1
;
48)
1
2
3
+
=
x
x
y ;
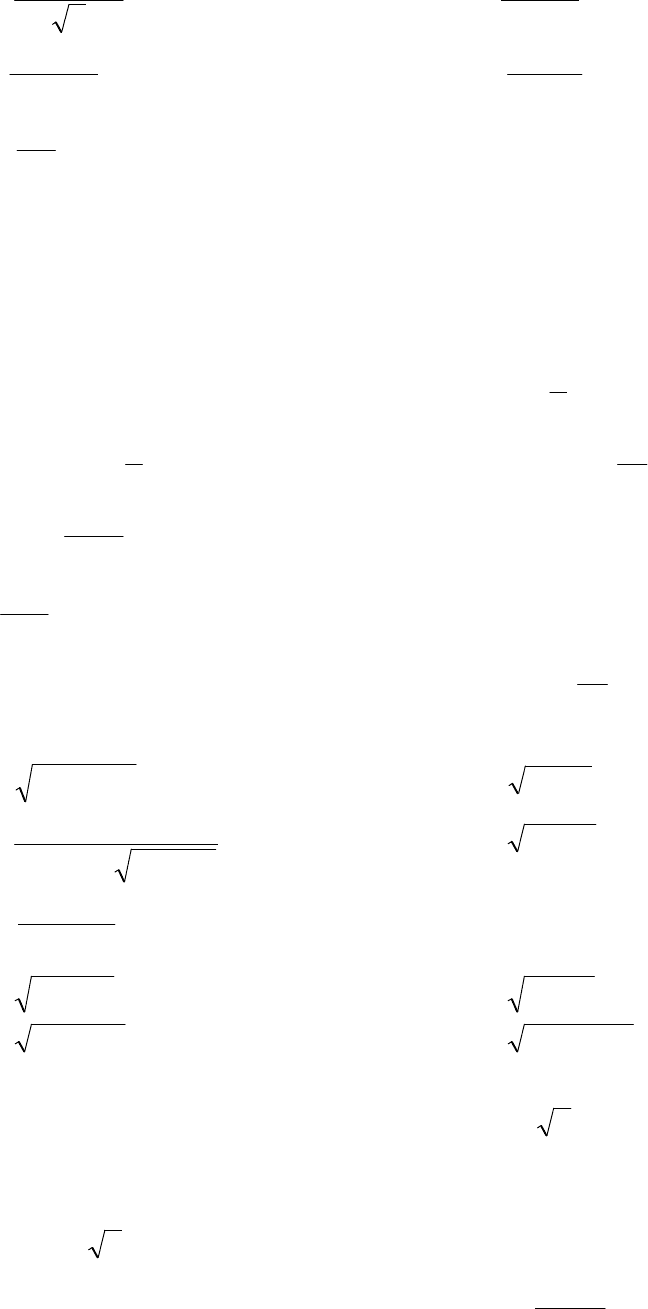
56
49)
x
x
y
2log
5
+
=
;
50)
x
x
y
ln1
+
= ;
51)
x
x
y
arcsin
= ; 52)
1
2
+
=
x
arctgx
y ;
53)
x
x
y
2
3
3
2
= ;
54)
xx
y 53
2
⋅= .
3.8. Используя правило вычисления производной сложной функ-
ции, переписать таблицу производных, заменив в функциях аргумент
x
на
функцию
(
)
xu .
3.9. Найти производные сложных функций:
1)
x
y
6
sin
=
; 2)
3
cos6
x
y = ;
3)
2
sin2cos
x
xy −= ; 4)
2
3
sin3cos
x
xy += ;
5)
+
=
3
2
2
x
ctgy ;
6)
(
)
53
+
=
xtgy ;
7)
2
13 +
=
x
e
y ;
8)
75
2
+
=
x
y ;
9)
(
)
75lg
+
=
xy ;
10)
2
5
arcsin
x
y = ;
11)
(
)
7
51 xy −= ; 12)
(
)
10
32 xy += ;
13)
(
)
3
2
34 xy += ;
14) xy 21−= ;
15)
( ) ( )
5
1414
1
+⋅+
=
xx
y ;
16)
(
)
2
5252 +⋅+= xxy ;
17)
( )
5
2
1
2
x
y
−
= ;
18)
(
)
3
2
51 xy += ;
19)
4
2
31 xy += ; 20)
3
4
1 xy += ;
21) 1cos += xy ; 22)
5
sin2 xxy −= ;
23) xtgy
6
= ; 24) xy
2
sin= ;
25)
x
tg
y
ln
=
;
26) xy sin= ;
27)
(
)
12ln
3
++= xxy ;
28)
x
y
cos
ln
=
;
29)
x
ey
sin
= ; 30)
arctgx
ey = ;
31) xy arccos= ;
32)
(
)
xy sinarcsin
=
;
33)
( )
xxy 2ln
2
+= ;
34)
2
ln
5
5
+
=
x
x
y ;
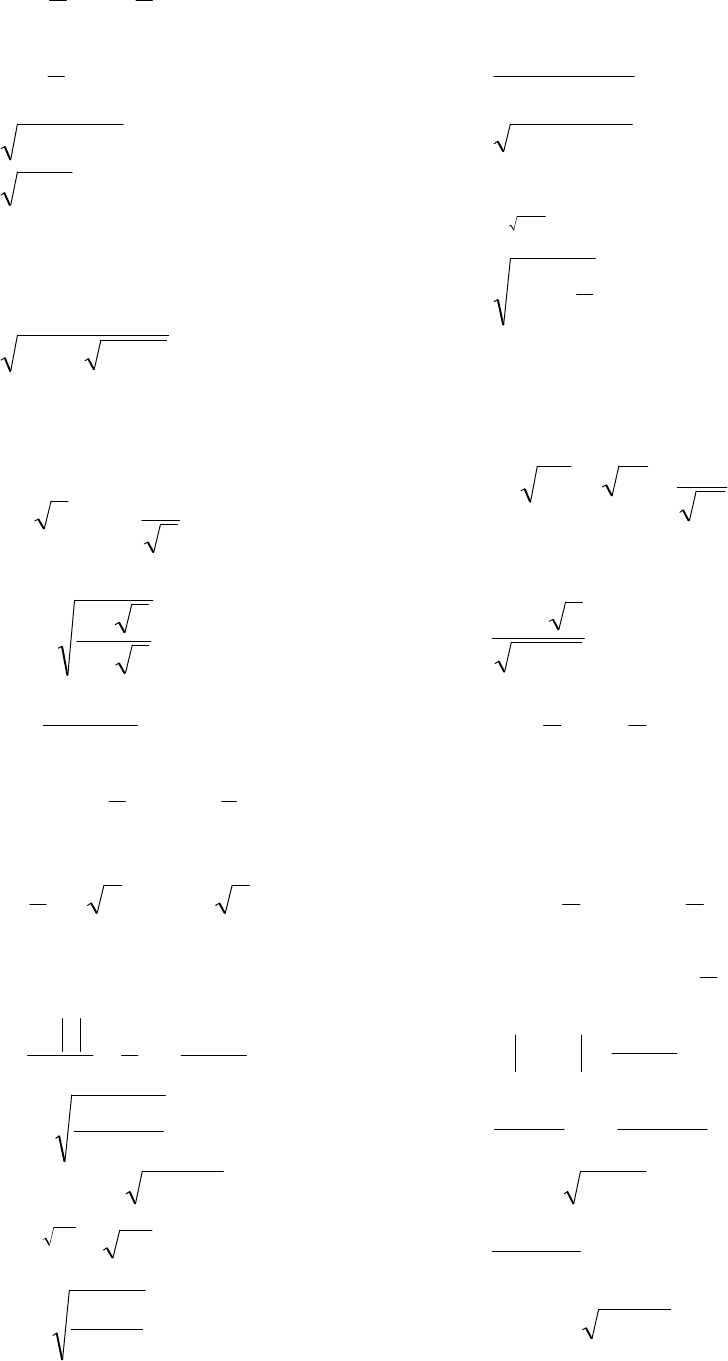
57
35)
2
2
cos
2
sin
+=
xx
y ;
36) xctgxtgy
22
+= ;
37)
3
sin
3
x
y = ; 38)
( )
6
4cos1
1
x
y
+
= ;
39)
4
2
cos1 xy += ;
40)
5
2sin5 xxy −= ;
41) xtgy 2= ;
42)
(
)
13ln
+
=
xctgy ;
43)
xtg
y
3
5= ;
44)
x
y
sin
2= ;
45)
(
)
x
ey
3
arcsin= ;
46)
2
x
arctgy =
47)
5
2
1cosln xy += ;
48)
15
sinln
+
=
x
tgey .
Найти производные функций.
3.10.
(
)
+⋅−= 1
1
1
x
xy .
3.11.
+⋅⋅=
3
2
3
2
3
4
2
3
x
xxy
3.12.
x
x
y
+
−
⋅=
1
1
2 .
3.13.
2
3
2
+
+
=
x
xx
y .
3.14.
2
cos1
sin
+
=
x
x
y . 3.15.
2
2
cos
2
sin
−=
xx
y .
3.16.
x
tgxtgxtgy 2
5
1
2
3
2
2
53
++=
.
3.17.
xxx
eeey
−−−
⋅−= cossin .
3.18. xxtgy cosln
2
1
2
+= . 3.19.
2
sinln2
2
2
xx
ctgy −−= .
3.20.
(
)
xxxy lncoslnsin
−
⋅
=
.
3.21.
2
lnlncos
x
tgtgxxy −⋅= .
3.22.
2
2
2
1
ln
2
1
1
ln
x
x
x
x
y
+
⋅−
+
= .
3.23.
1
1
1ln
2
2
−
−−=
x
xy .
3.24.
x
x
y
sin
1
sin1
ln
−
+
= .
3.25.
x
x
x
x
y
cos
sin1
ln
cos
sin
2
+
+= .
3.26.
(
)
193ln
42
++= xxy . 3.27.
(
)
1ln
2
++= xxy .
3.28.
(
)
12
2
−⋅= xey
x
.
3.29.
xx
xx
e
e
ee
y
−
−
−
+
= .
3.30.
1
ln
4
4
+
=
x
x
e
e
y .
3.31.
(
)
1ln
42
++=
xx
eey .

58
3.32.
2
4
2
arccos x
x
xy −−⋅=
.
3.33. xxxy −+⋅= 1arcsin
.
3.34.
( )
2
1
1
2
++
+
++=
x
x
x
xarctgy
.
3.35.
2
2
9
9
arccos
x
x
y
+
−
= ,
0
>
x
..
3.36.
( )
( )
2
2
2
1
1ln
2
1
arctgxxarctgxxy ⋅−+−⋅= .
3.37.
(
)
( )
2
3
1
11ln +⋅−⋅+++= xxxy
.
3.38.
(
)
(
)
( )(
42
31
ln
3
3
−−
−−
=
xx
xx
y
.
3.39. Найти значения производных функций в указанных точках:
1)
(
)
2
2 xxxf −+= , найти
(
)
0f
′
,
(
)
1f
′
,
(
)
10f
′
;
2)
()
(
)
x
x
xf
2
1−
= , найти
(
)
01,0f
′
;
3)
()
t
t
tf
sin
1
cos
−
= , найти
′
6
π
f ;
4)
(
)
(
)
(
)
(
)
32
321 −⋅−⋅−= xxxxf , найти
(
)
1f
′
,
(
)
2f
′
,
(
)
3f
′
;
5)
()
1
2
ln
+
=
t
t
e
e
tf , найти
(
)
0f
′
;
6)
(
)
xxxf 2cos2sin
33
−= , найти
′
8
π
f ;
7)
4
1
1
ln
2
1
x
x
arctgxy
−
+
−= , найти
−
′
2
1
y ;
8*)
x
exy ⋅= , найти
(
)
1
−
′
y ,
(
)
1y
′
,
(
)
0
−
′
y ,
(
)
0
+
′
y .
3.40. Вычислить
(
)
(
)
02 uu
′
+
′
, если
2
arcsin44
2
x
xxu +−= .
3.41. * Для функции xxy coscos2 += вычислить
′
6
π
y ,
′
4
3π
y ,
′
−
2
π
y ,
′
+
2
π
y и определить, существует ли производная функции в
точке
2
π
=x .
3.42. Количество продукции Q (ед.), произведённой бригадой рабо-
чих в течение дня описывается функцией tttQ 755
23
++−= , где t − время
(ч),
8
0
≤
≤
t
. Найти производительность труда бригады рабочих через 1, 2,
4, 6 часов после начала работы. Сделать экономический анализ.

59
3.43. Известна зависимость расхода автомобилем горючего на 100
км пути от скорости движения автомобиля:
(
)
2
005,04,020 xxxf +−= , где
−
x
скорость в км/ч,
(
)
−
xf расход горючего в литрах на 100 км. Найти за-
кон изменения скорости расхода горючего. Сравнить скорости расхода го-
рючего при движении со скоростью 60 км/ч и 80 км/ч.
3. Логарифмической производной функции
(
)
xfy
=
называют про-
изводную натурального логарифма модуля этой функции:
(
)
(
)
(
)
()
(
)
′
=
′
=
y
y
dx
yd
xf
xf
dx
xfd lnln
.
Логарифмическую производную используют при вычислении про-
изводных функций, содержащих операции умножения, деления, возведе-
ния в степень. Найдём, в частности, производную показательно-степенной
функции ,
v
uy= где
u
и
v
- функции независимой переменной
x
:
(
)
xuu
=
,
(
)
xvv
=
,
0
>
u
. Прологарифмируем равенство ,
v
uy= получим
u
v
y
ln
ln
=
. Найдём производные левой и правой частей:
⇒
′
⋅+⋅
′
=
′
u
u
v
uv
y
y
ln
′
⋅+⋅
′
=
′
u
u
v
uvyy ln или, подставляя
v
uy = :
′
⋅+⋅
′
=
′
u
u
v
uvuy
v
ln .
Пример 3.5. Используя логарифмическую производную, найти про-
изводные следующих функций: 1)
(
)
0
sin
>= xxy
x
; 2)
(
)
2
2
1
1
x
xx
y
−
+
= .
Решение. 1) Логарифмируя исходную функцию, получим
x
x
y
ln
sin
ln
⋅
=
.
Отсюда
x
x
xx
y
y sin
lncos +⋅=
′
,
x
x
x
x
xxyy
x
x
xxy
sin
sin
lncos
sin
lncos ⋅
+⋅=
′
⇒⋅
+⋅=
′
.
2) Имеем
(
)
22
1ln
2
1
1lnlnln xxxy −−++= , тогда
( )
⇒
−
−+
=
−
+
+
+=
′
4
42
22
1
231
11
21
xx
xx
x
x
x
x
xy
y
( )
4
42
1
)231(
xx
xx
yy
−
−+
⋅=
′
(
)
22
42
11
231
xx
xx
y
−−
−+
=
′
⇒
.

60
3.44. Найти производные функций:
1)
x
xy = ;
2)
(
)
(
)
( )
3
2
1
123
+
−−
=
x
xx
y ;
3)
(
)
x
xy sin= ; 4)
(
)
x
xy
1
ln= ;
5)
( )( )
3
5
2
12
x
xx
y
−⋅+
=
;
6)
3
3
sin
1
3sin
x
x
y
−
= ;
7)
x
e
xy = ;
8)
x
xy = ;
9)
(
)
x
xy
arcsin
sin= ; 10)
(
)
x
x
xy = ;
11)
(
)
x
x
x
x
y
ln
ln
= ; 12)*
(
)
(
)
(
)
xx
xx
xxy 2
2
2
++= .
3. 3. Производные высших порядков
Если производная функции
(
)
xfy
=
определена и является функци-
ей, дифференцируемой в точке
x
, то её производную называют производ-
ной 2-го порядка (или 2-ой производной) функции
(
)
xfy
=
в точке
x
:
() ()( )
′
′
=
′′
xfxf . Если
(
)
xf
′
′
является дифференцируемой в точке
x
, то про-
изводная 3-го порядка
() ()( )
′
′′
=
′′′
xfxf и т.д.
В общем случае: если производная
(
)
1
−
n -го порядка
(
)
(
)
xf
n 1
−
диф-
ференцируема в точке
x
, то её производную называют производной
n
-го
порядка (или
n
-ой производной) функции
(
)
xfy
=
в точке
x
:
()
()
( )
()
(
)
′
=
−
xfxf
nn 1
,
.
,...
3
,
2
=
n
Обозначают
n
-ую производную
(
)
(
)
(
)
xfy
nn
, ,
n
n
dx
yd
или
(
)
n
n
dx
xfd
.
Производные, начиная со второй, называют производными высших поряд-
ков.
Пример 3.6. 1) Найти производную второго порядка функции
x
exy
−
⋅= ;
2) для функции ,53
23
+−= xxy найти ,...,yy
′
′
′
;
3) для функции
x
y 2= , найти
(
)
n
y ;
4) для функции xey
x
3sin
2
⋅= , найти
(
)
0y
′
,
(
)
0y
′
′
,
(
)
0y
′
′
′
.
Решение. 1)
(
)
;1
xxx
exexey
−
−
−
−=⋅−=
′
( )
(
)
′
−=
′′
−x
exy 1 =
(
)
(
)
xxx
exexe
−
−
−
−=−−− 21 .
2) Последовательно вычислим ,63
2
xxy −=
′
(
)
,6,16
=
′
′
′
−
=
′
′
yxy
.0...===
VIV
yy
