Никифорова И.А. Математика в экономике: сборник задач. Часть ?
Подождите немного. Документ загружается.

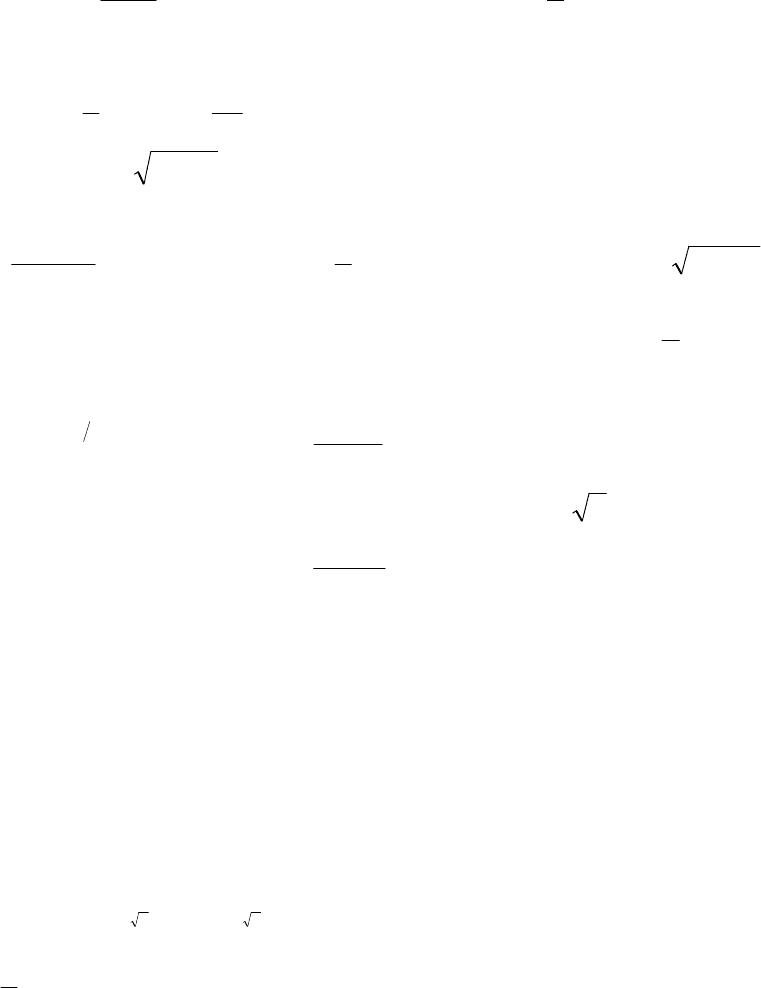
61
3) Имеем 2ln2 ⋅=
′
x
y , 2ln2
2
⋅=
′′
x
y , ... ,
(
)
2ln2
nxn
y ⋅= .
4) Имеем
(
)
xxey
x
3cos33sin2
2
+⋅=
′
,
(
)
xxxxey
x
3sin93cos63cos63sin4
2
−++⋅=
′′
(
)
xxe
x
3sin53cos12
2
−= ,
(
)
xxxxey
x
3cos153sin363sin103cos24
2
−−−=
′′′
(
)
xxe
x
3sin463cos9
2
−= .
Подставляя
0
=
x
в найденные производные, получим
(
)
,30
=
′
y
(
)
,120
=
′
′
y
(
)
90
=
′
′
′
y .
3.45. Найти производные второго порядка:
1)
5
22
+
−=
x
y ; 2)
( )
3ln2
4
1
2
−= xxy ;
3) xy
2
cos= ;
4)
2
xarctgy = ;
5) xxxy 3cos
27
2
3sin
9
1
−= ;
6)
2
x
ey
−
= ;
7)
3
2
2
1log xy −= ;
8)
(
)
xxxy lncoslnsin
+
=
.
3.46. Найти производные третьего порядка:
1)
( )
16 +
=
x
x
y
;
2) xy
2
ln
2
1
= ; 3)
(
)
3232 ++= xxy ;
4)
t
te
s
−
=
;
5)
x
x
y
sin
⋅
=
; 6)
2
x
arctgy = .
3.47. Найти производные
n
-го порядка:
1)
2x
ey = ;
2)
1
2
1
+
=
x
y ;
3)
xx
y
−
+= 22 ;
4)
(
)
n
xy 14 += ; 5)
x
y
2
ln
=
; 6) xxy
n
⋅= ;
7) xy
2
cos35−= ;
8)
d
cx
bax
y
+
+
= (
d
c
b
a
,
,
,
-постоянные).
3.48. Найти производные в указанных точках:
1)
(
)
1ln
−
=
xy , найти
(
)
2y
′
′
;
2) xxy ln
3
⋅= , найти
(
)
y
IV
1 ;
3)
(
)
xexy
x
3sin
2
⋅= , найти
(
)
0y ,
(
)
0y
′
,
(
)
0y
′
′
.
3.49. Показать, что функция
(
)
xfy
=
удовлетворяет заданному
уравнению, если:
1)
x
x
y
2
sin
+
=
, xyy 44
=
+
′
′
;
2)
x
x
y
ln
cos
ln
sin
+
=
, 0
2
=+
′
+
′′
yyxyx ;
3)
xx
eey
2
2+= , 06116
=
−
′
+
′
′
−
′
′
′
yyyy ;
4)
xx
eСeСy
⋅−
+=
2
21
, здесь C
1
, С
2
–произвольные постоянные,
0
2
1
=−
′
+
′′
yyyx .

62
3.50. Пусть
(
)
−
uf дважды дифференцируемая функция. Найти y
′
и y
′
′
, если: 1)
=
2
1
x
fy ; 2)
(
)
xfy ln
=
.
3.51. Пусть
(
)
xu и
(
)
−
xv дважды дифференцируемые функции.
Найти y
′
и y
′
′
, если: 1) ;ln
v
u
y = 2*)
22
vuy += .
3.52. * Пусть функции
(
)
xu и
(
)
xv имеют производные до
−
n
го
порядка включительно. Показать, что справедлива формула Лейбница:
( )
()
() ( )
(
)
( ) () ( )
kkn
n
k
k
n
nnnn
n
vuCvuvu
nn
vunvuvu ⋅⋅=⋅++
′′
⋅
−
+
′
⋅+⋅=⋅
−
=
−−
∑
0
21
...
21
1
,
где
(
)
u
u
=
0
,
(
)
v
v
=
0
,
(
)
(
)
( )
!!
!
...21
1...1
knk
n
k
knnn
C
k
n
−
=
⋅⋅⋅
+
−
−
= .
Применяя формулу Лейбница, найти производные указанных поряд-
ков от заданных функций:
1)
(
)
xxxy sin1
2
⋅++= , найти
(
)
15
y ; 2)
(
)
x
exxy ⋅−=
2
, найти
(
)
20
y ;
3) xey
x
sin
−
= , найти
(
)
5
y ; 4) xxy
2
log
⋅
=
, найти
(
)
10
y .
3.4. Дифференцирование функций, заданных неявно и
параметрически
1. Дифференцирование функций, заданных неявно. Пусть диффе-
ренцируемая функция
(
)
,xyy
=
X
x
∈
, задана неявно посредством уравне-
ния
(
)
0,
=
yxF . (3.2)
Для нахождения производной
(
)
xyy
′
=
′
следует продифференциро-
вать равенство (3.2) по
x
, рассматривая левую часть как сложную
функцию переменной
x
:
(
)
=
yxF ,
(
)
(
)
xyxF , , а затем разрешить относи-
тельно y
′
полученное в результате уравнение
(
)
(
)
0
,
=
dx
xyxdF
.
Для нахождения второй производной следует при тех же предполо-
жениях последовательно дважды продифференцировать уравнение (3.2)
по
x
и выразить из полученной системы уравнений
(
)
(
)
()( )
=
=
0
,
,0
,
2
dx
xyxFd
dx
xyxdF
y
′
′
как функцию
y
и
x
. Аналогично вычисляются производные более вы-
соких порядков.

63
Пример 3.7. Найти
(
)
xy
′
и
(
)
xy
′
′
, если 05 =−−⋅ yex
y
.
Решение. Дифференцируем уравнение дважды по
x
, считая
y
функ-
цией от переменной
x
, последовательно получим:
0=
′
−
′
⋅⋅+ yyexe
yy
,
(
)
0
2
=
′′
−
′′
⋅⋅+
′
⋅⋅+
′
⋅+
′
⋅ yyexyexyeye
yyyy
.
Из первого равенства получим
y
y
e
x
e
y
⋅
−
=
′
1
, из второго
(
)
y
y
e
x
eyyx
y
⋅
−
⋅
′
⋅
′
⋅+
=
′′
1
2
или, после подстановки найденного для y
′
выраже-
ния:
(
)
( )
3
2
1
2
y
yy
ex
eex
y
⋅−
⋅⋅−
=
′′
.
3.53. Найти
(
)
xy
′
для следующих функций, заданных неявно:
1) 0
223
=++ yyxx ;
2)
0
ln
=
+
−
xy
e
x
; 3) 1
25
=−+ xyy ;
4) ;
2244
yxyx ⋅=+
5) 7=++ yxyx ; 6) =
x
y
arctg
22
ln yx + ;
7) ,
3/23/23/2
ayx =+
−
a
параметр;
8)
22
ln yx
x
y
⋅= ; 9)
(
)
;cos xxy
=
10)
(
)
yxy
+
=
cos ;
11) exye
y
=+ , найти
(
)
0y
′
;
12) 024104
22
=+−−+ yxyx , найти
(
)
0y
′
, если
(
)
60
=
y .
3.54. Найти
(
)
xy
′
′
для следующих функций, заданных неявно:
1)
0
=
+
−
x
y
arctgy
;
2) xyee
yx
−=− ;
3) 0552
223
=−++− yxyxx , найти
(
)
0y
′
′
;
4) 0625
22
=−+−++ yxxyyx , найти
(
)
1y
′
′
, если
(
)
11
=
y .
2. Дифференцирование функций, заданных параметрически. Если
система
(
)
()
=
=
,
,
ty
tx
ψ
ϕ
(
)
bat ,
∈
,
где
(
)
t
ϕ
и
(
)
−
t
ψ
дифференцируемые функции и
(
)
0
≠
′
t
ϕ
, определяет
y
как
однозначную функцию от
x
, то производная
(
)
xy
′
существует и определя-
ется условиями
(
)
()
()
′
′
==
′
=
,
,
t
t
dx
dy
y
tx
ϕ
ψ
ϕ
(
)
bat ,
∈
.
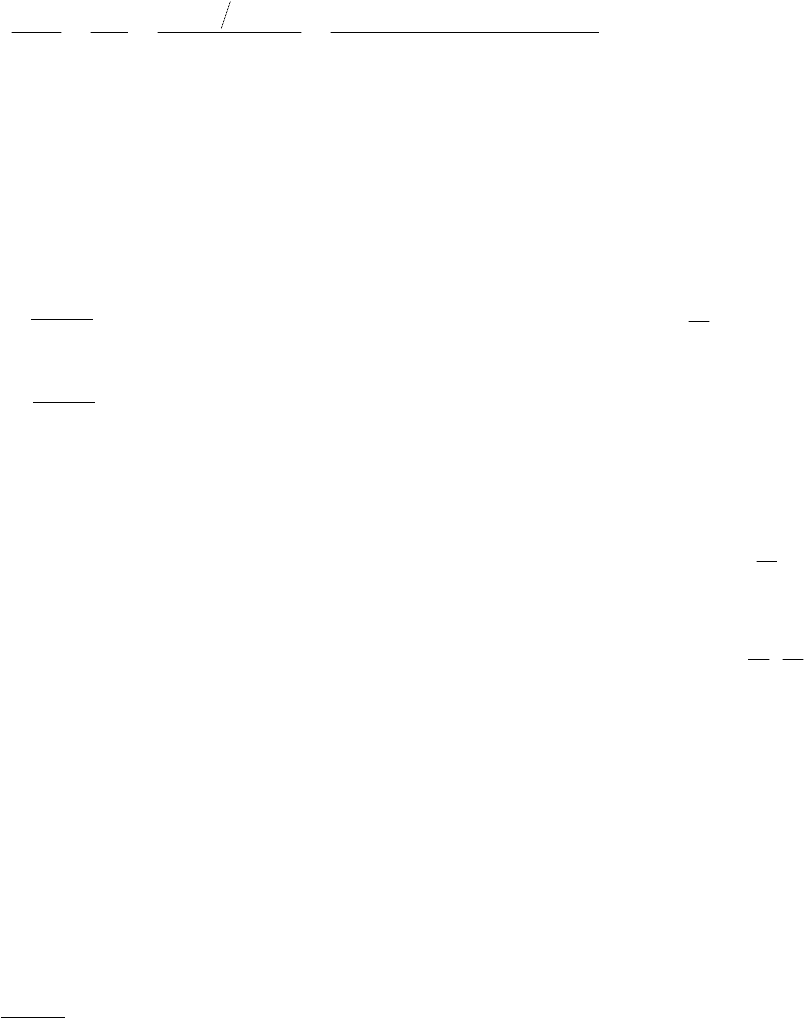
64
Производные высших порядков (если они существуют) вычис-
ляются последовательно:
(
)
() ()( )
()
() () () ()
()( )
′
′
⋅
′′
−
′
⋅
′′
=
′
′
′′
=
′
==
′′
=
,
,
32
2
t
tttt
t
tt
dx
yd
dx
yd
y
tx
ϕ
ψϕϕψ
ϕ
ϕψ
ϕ
(
)
bat ,
∈
и т. д.
3.55. Для следующих функций, заданных параметрически, найти
производные первого порядка от
y
по
x
:
1)
+−=
++=
,13
,13
3
3
tty
ttx
(
)
∞
+
∞
−
∈
,t ;
2)
(
)
( )
−=
−
=
,cos12
,sin2
ty
ttx
(
)
∞
+
∞
−
∈
,t ;
3)
+
=
+
=
,
1
3
,
1
3
3
2
3
t
t
y
t
t
x
1
−
≠
t
;
4)
+=
=
;
,ln2
ctgttgty
ctgtx
∈
2
,0
π
t .
3.56. Для следующих функций, заданных параметрически, найти
производные второго порядка от
y
по
x
:
1)
( )
+=
+=
,1ln
,2
2
ty
ttx
(
)
∞
+
−
∈
,1t ;
2)
=
=
,sin3
,cos2
3
3
ty
tx
∈
2
,0
π
t ;
3)
+=
+=
−
,6
,1
6
6
t
t
ety
ex
(
)
∞
+
∞
−
∈
,t ; 4)
=
=
,sin
,cos
tey
tex
t
t
−∈
2
,
2
ππ
t .
3.5. Дифференциал функции. Дифференциалы высших порядков
1. Дифференциал функции. Функцию
(
)
xfy
=
называют диффе-
ренцируемой в точке
x
, если её приращение в этой точке
(
)
(
)
xfxxfy
−
∆
+
=
∆
представимо в виде
(
)
(
)
xoxxAy
∆
+
∆
⋅
=
∆
, (3.3)
где
(
)
0→
∆
∆
x
xo
при
0
→
∆
x
. При этом главную при
(
)
0
≠
xA , линейную
относительно
x
∆
, часть приращения функции называют её дифференциа-
лом (или дифференциалом первого порядка) и обозначают символом
(
)
xdf или
dy
:
(
)
.xxAdy
∆
⋅
=
Приращение независимой переменной
x
на-
зывают её дифференциалом и обозначают символом
:
dx
.
x
dx
∆
=
Для дифференцируемости функции
(
)
xfy
=
в точке
x
необходи-
мо и достаточно, чтобы в этой точке существовала конечная производная
(
)
xfy
′
=
′
, при этом верно равенство

65
(
)
(
)
dxxfxdf
′
=
(
)
(
)
dxxfdy
′
=
. (3.4)
2. Формулы для приближённых вычислений. Если приращение
x
∆
достаточно мало по абсолютной величине, то для дифференцируемой
функции
(
)
xfy
=
имеют место приближённые формулы для вычисления
приращения функции в точке
x
:
(
)
(
)
xdfxf
≈
∆
(
)
dyy
≈
∆
и значения функции в точке
x
x
∆
+
:
(
)
(
)
(
)
xxfxfxxf
∆
⋅
′
+
≈
∆
+
.
(3.5)
Разности
(
)
(
)
xdfxf −∆
и
(
)
(
)
xxfxf ∆⋅
′
−∆
равны абсолютным, а
отношения
(
)
(
)
()
xf
xdfxf
∆
−∆
и
(
)
(
)
( )
xxf
xxfxf
∆+
∆⋅
′
−∆
− относительным погреш-
ностям этих вычислений.
Пример 3.8. Найти приращение и дифференциал функции
13
3
−+= xxy в точке
1
=
x
при
.
1
,
0
=
∆
x
Вычислить абсолютную и от-
носительную погрешности, которые допускаются при замене приращения
функции её дифференциалом.
Решение. При произвольных
x
и
x
∆
имеем:
(
)
[
]
(
)
=−+−−∆++∆+=∆ 1313
3
3
xxxxxxy
(
)
(
)
xxxxxx ∆+∆+∆⋅+∆⋅
32
2
399 ,
(
)
.19
2
xxdy ∆⋅+=
При
1
,
0
,
1
=
∆
=
x
x
получаем
,
093
,
1
1
,
0
003
,
0
09
,
0
9
,
0
=
+
+
+
=
∆
y
,
1
=
dy
093
,
0
=
−
∆
dy
y
.
Абсолютная погрешность
,093,0=−∆ dyy
относительная погреш-
ность равна 085,0
093,1
093,0
≈=
∆
−∆
y
dyy
или приближённо 8,5%.
Пример 3.9. Найти
dy
, если
(
)
x
exxy
−
⋅−−=
2
22 .
Решение. Воспользуемся формулой (3.4):
(
)
(
)
( )
(
)
(
)
⇒−−−−−=
′
−−=
−−−
dxexxexdxexxdy
xxx 22
222222
(
)
.4
2
dxexdy
x
−
−=
Пример 3.10. Вычислить приближённое значение
.
51
,
0
arcsin
Решение. Рассмотрим функцию
.
arcsin
x
y
=
Полагая
01
,
0
,
5
,
0
=
∆
=
x
x
, применим формулу (3.5):
(
)
≈
∆
+
xxarcsin
( )
,arcsinarcsin xxx ∆⋅
′
+
получим
≈
51
,
0
arcsin
( )
.513,0011,0
6
01,0
5,01
1
5,0arcsin
2
≈+=⋅
−
+
π
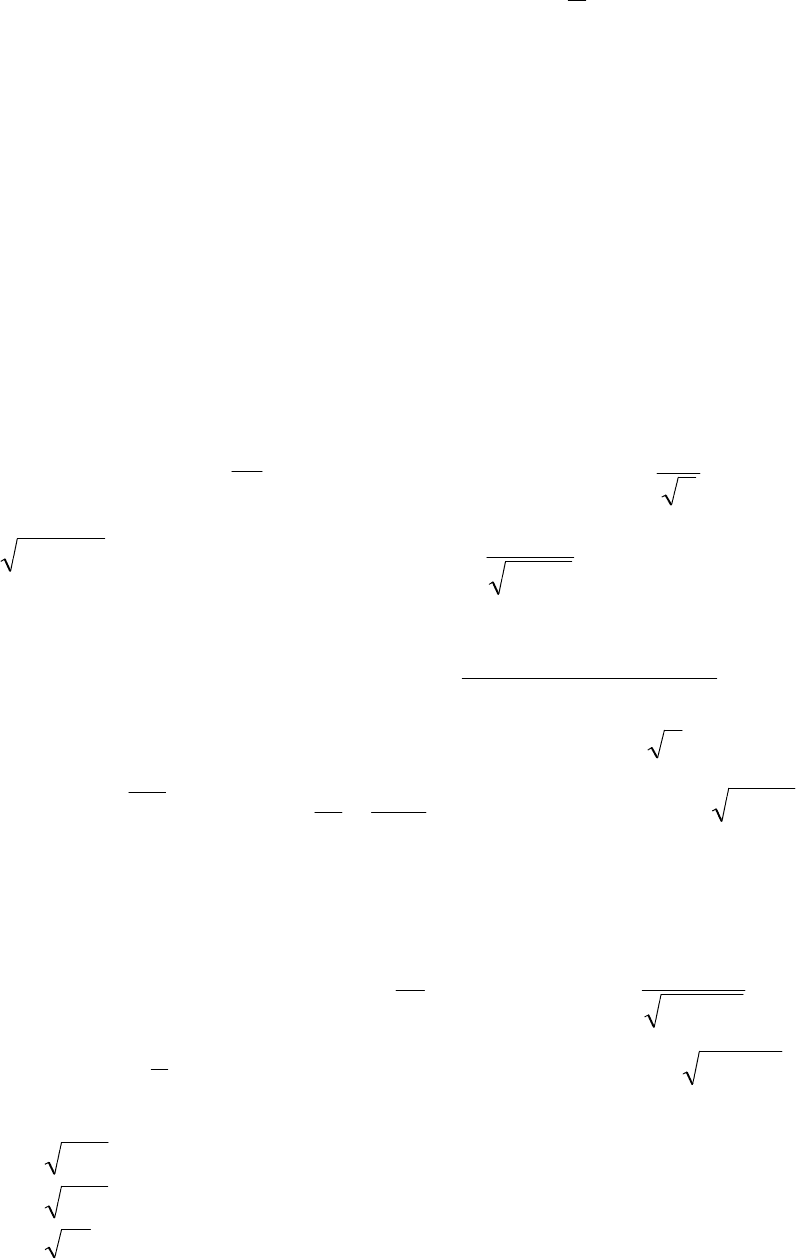
66
3.57. Доказать, что для линейной функции
b
ax
y
+
=
приращение
y
∆
и дифференциал
dy
совпадают.
3.58. Найти приращения и дифференциалы функций
(
)
xfy
=
в
точке
0
x, соответствующие трём различным приращениям аргумента
а)
1
=
∆
x
, б)
1
,
0
=
∆
x
, в)
01
,
0
=
∆
x
, если: 1)
x
y
1
=
, 1
0
=
x ; 2)
3
xy = ,
2
0
=
x . Вычислить абсолютные
a
∆
и относительные
δ
погрешности, кото-
рые допускаются при замене приращения функции её дифференциалом.
3.59. Дать толкование дифференциала функции
(
)
0
tdf , соответст-
вующего приращению аргумента
t
∆
(
)
0
>
∆
t , если:
1) функция
(
)
tfs
=
описывает закон прямолинейного движения ма-
териальной точки, где
t
(ч) − время движения, а
s
(км) − пройденный путь
за промежуток времени от 0 до
t
;
2) функция
(
)
tfQ
=
описывает зависимость между временем работы
рабочего
t
(ч) и объёмом продукции
Q
(ед.), произведённым им за проме-
жуток времени от 0 до
t
.
3.60. Найти:
1)
(
)
x
exd ⋅ ;
2)
3
1
x
d ;
3)
(
)
2
1ln xd − ; 4)
x
x
d
ln
;
5)
(
)
−+ axad ,
22
параметр;
6)
−
2
1 x
x
d .
3.61. Найти
dy
, если:
1)
4
cos
sin
+
−
=
x
x
x
y
; 2)
(
)
8
2cos2sin2
2
xxe
y
x
−−
= ;
3)
x
earctgy
2
= ; 4)
1
ln
+
−
=
x
x
x
y
; 5) xxy sin
2
= ;
6)
x
ey
cos
1
−
= ; 7)
6
6
ln
12
1
+
−
=
x
x
y
; 8) .31arcsin
2
−−+⋅= xxxy
3.62. Пусть
−
w
v
u
,
,
дифференцируемые функции переменной
x
.
Найти дифференциал функции
y
, если:
1)
w
v
u
y
⋅
⋅
=
;
2)
2
v
u
y = ; 3)
22
1
vu
y
+
= ;
4)
v
u
arctgy =
;
5)
(
)
wvu
ey
+
= ; 6)
22
ln vuy += .
3.63. Найти приближённые значения:
1) ;02,1
3
2)
;
05
,
1
arctg
3) ;46
0
tg
4) ;8,15
4
5) ;29sin
0
6)
;
2
,
1
ln
7) ;33
5
8) ;0145
0
′
ctg
9)
(
)
.03,1
5

67
3.64. Найти приближённое значение функции
(
)
xfy
=
в точке
0
x ,
если:
1)
(
)
;2,1,
0
2
==
−
xexf
xx
2)
()
.15,0,
2
2
0
5
=
+
−
= x
x
x
xf
3.65. Найти приближённо путь
s
∆
(км), пройденный материальной
точкой
M
за промежуток времени от 3
1
=
t ч до 4
2
=
t ч, если точка
M
дви-
жется прямолинейно по закону
ts 31 +=
, где
t
(ч) − время движения,
а
s
(км) − пройденный путь за промежуток времени от 0 до
t
.
3.66. Вычислить приближённое значение площади круга, радиус ко-
торого равен 3,02 м.
3.67. Найти приближённое значение объёма шара радиуса 2,01 м.
3.68. Рёбра куба увеличены на 1 см. При этом дифференциал
dV
объёма
V
куба оказался равным 12 см
3
. Найти первоначальную длину
рёбер.
3.69. Радиус круга увеличен на 1 см. Дифференциал площади круга
оказался при этом равным 6π см
2
. Найти первоначальную величину радиу-
са.
3. Дифференциалы высших порядков. Дифференциалы высших
порядков функции
(
)
xfy
=
последовательно определяют равенствами:
(
)
,
2
dydyd =
(
)
,
23
yddyd = ... ,
(
)
,
1
yddyd
nn
−
= ... .
откуда получаем формулы для вычисления дифференциалов:
,
22
dxyyd
′′
= ,
33
dxyyd
′′
= ... ,
(
)
....,
nnn
dxyyd =
3.70. Найти дифференциалы второго порядка функций:
1) ,
2
cbxaxy ++= (
−
c
b
a
,
,
пара-
метры);
2)
2
3
x
y
−
= ;
3)
(
)
,sin cbxay
+
=
(
−
c
b
a
,
,
пара-
метры);
4)
2
1 xy += ;
5)
x
x
y
ln
=
; 6)
2
3
1
2
+
−
=
x
x
y ;
7) xxy arcsin1
2
⋅−= ;
8)
(
)
4ln
2
++= xxy ;
9)
x
xy = .
3.71. Найти дифференциалы третьего порядка функций:
1)
(
)
1ln
−
=
xxy ;
2) xy
2
sin= ;
3)
.
1
x
y =
3.72. Пусть
(
)
−
=
xuu функция, дифференцируемая достаточное
число раз. Найти yd
3
, если:
1)
(
)
ufy
=
; 2)
u
y
ln
=
;
3) ;
u
ey = 4)
2
uy = .
3.73. Найти дифференциалы 1-го и 2-го порядков функций:
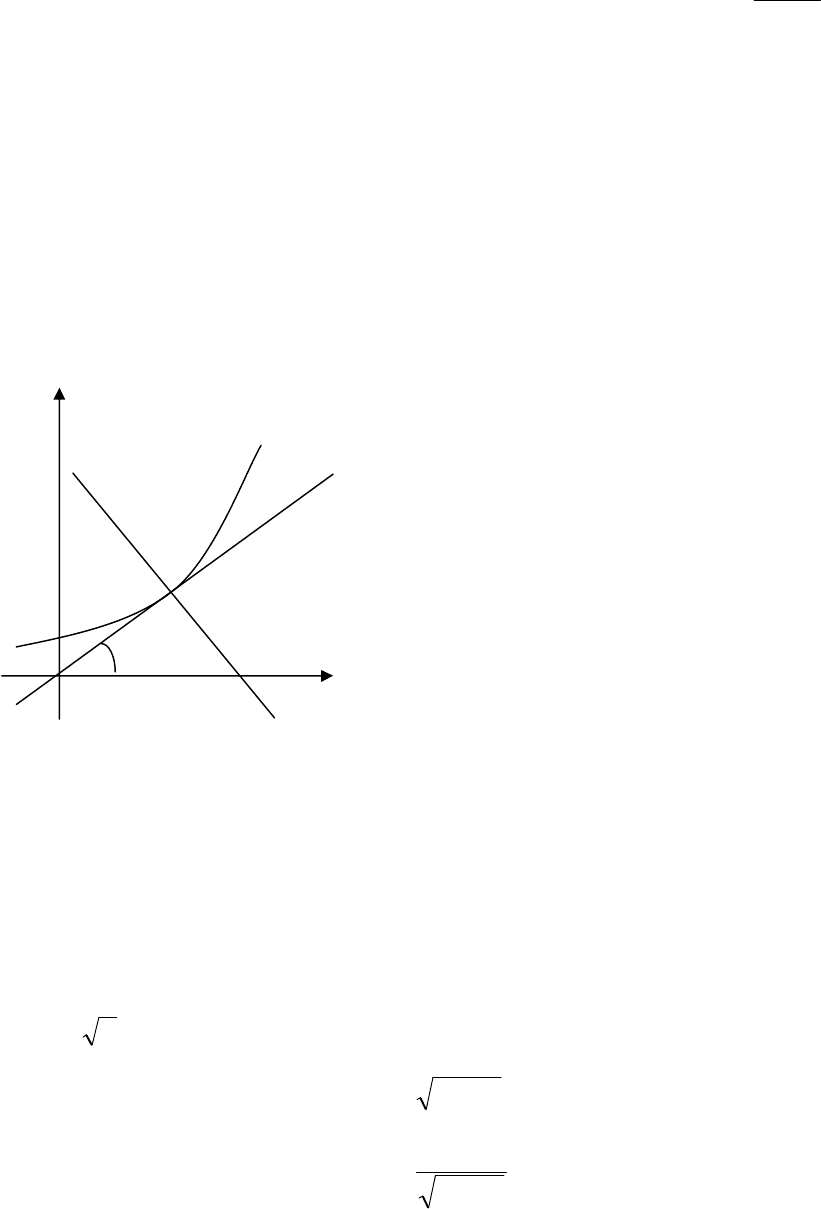
68
1) ;
2x
ey = 2) ;374
25
+−= xxy
3)
2
2
1
1
ln
x
x
y
+
−
=
.
считая, что а)
−
x
независимая переменная; б)
−
x
функция от переменной
t
.
3.74. Найти дифференциалы 1-го и 2-го порядков следующих неявно
заданных функций: 1) 1
2
=+ yxy ; 2) yxe
y
+= .
3.6. Геометрические приложения производной
Значение производной
(
)
0
xf
′
функции
(
)
xfy
=
равно угловому ко-
эффициенту
ϕ
tg
k
=
касательной
T
T
′
к графику этой функции, проведён-
ной через точку
(
)
000
, yxM , где
(
)
00
xfy
=
, см. рис. 3.1 (геометрический
смысл производной).
Уравнение касательной
T
T
′
к гра-
фику функции
(
)
xfy
=
в его точке
(
)
000
, yxM имеет вид
(
)
(
)
000
xxxfyy
−
′
=
−
.
Уравнение нормали NN
′
к графику функ-
ции
(
)
xfy
=
в его точке
(
)
000
, yxM :
(
)
(
)
0
000
=
−
′
+
−
yyxfxx .
Углом между двумя кривыми в их об-
щей точке называют угол между каса-
тельными к этим кривым в рассматри-
ваемой точке.
3.75. Написать уравнение касательной и нормали к графику функ-
ции
(
)
xfy
=
в точке
(
)
000
, yxM , если:
1) 45
2
+−= xxy , 1
0
−
=
x ;
2) 342
23
−−+= xxxy , 2
0
−
=
x ;
3) xy = , 4
0
=
x ;
4)
x
y
ln
=
, x
0
1
=
;
5)
x
tg
y
2
=
, 0
0
=
x .
6) y x= −5
2
, x
0
1
=
.
7)
2
1 x
ey
−
= , 1
0
−
=
x ;
8) y
x
=
−
2
9
2
3
, x
0
1
=
.
3.76. Написать уравнение касательной и нормали к параболе
2
4 xy −= в точке её пересечения с осью
Ox
(при
0
>
x
) и построить пара-
болу, касательную и нормаль.
Рис
. 3.1
x
y
T
T
′
N
N′
0
M
ϕ

69
3.77. В уравнении параболы cbxxy ++=
2
определить
b
и
c
, если
известно, что парабола касается прямой
x
y
=
в точке
2
=
x
.
3.78. Доказать, что угол
α
между кривыми
(
)
xfy
1
=
и
(
)
xfy
2
=
в их
общей точке
(
)
000
, yxM находится по формуле
(
)
(
)
( ) ( )
0201
0102
1 xfxf
xfxf
arctg
′
⋅
′
+
′
−
′
=α .
Найти угол между: 1) кривой
3
xxy −= и прямой
x
y
5
=
; 2) кривы-
ми
3
xy = и
2
1 xy = .
3.79. Определить:
1) в какой точке касательная к параболе xxy 4
2
+= параллельна оси
Ox
;
2) в какой точке параболы 52
2
+−= xxy нужно провести касатель-
ную, чтобы она была перпендикулярна к биссектрисе первого координат-
ного угла.
3.7. Элементы предельного или маргинального анализа
1. Основные понятия и формулы. Пусть
(
)
−
=
xfy функция эконо-
мического анализа,
0
,
0
>
>
y
x
.
Далее во всех формулах через
x
будем обозначать произвольное
фиксированное значение аргумента, а через
−
∆
x
его приращение.
1. Разность
(
)
(
)
(
)
xfxxfxfy
−
∆
+
=
∆
=
∆
называют абсолютным при-
ращением или абсолютным приростом зависимой переменной
y
(функции
(
)
xf ), соответствующим изменению аргумента от значения
x
до
x
x
∆
+
.
2. Отношение =
∆
∆
x
y
(
)
x
xf
∆
∆
задаёт среднее приращение (средний при-
рост или среднюю скорость изменения) зависимой переменной
y
(функ-
ции
(
)
xf ), соответствующее изменению аргумента от значения
x
до
x
x
∆
+
. Средний прирост функции равен изменению функции, приходяще-
муся на единицу приращения аргумента при изменении последнего от
x
до
x
x
∆
+
.
2а. Средняя величина зависимой переменной
y
(функции
(
)
xf )
()
(
)
x
xf
x
y
xAfAy === ,
равна значению зависимой переменной (функции), приходящемуся на еди-
ницу значения аргумента. Например, средняя выручка
AR
(
)
q
qR
=
, где
(
)
qR − выручка от продаж товара в объёме
q
, средние издержки

70
AC
(
)
Q
QC
=
, где
(
)
QC - издержки при выпуске продукции в объёме
Q
,
средний продукт труда
(
)
L
Lf
AQ = (для него часто используют обозначе-
ние AP
L
=AQ), где
(
)
−
=
LfQ производственная функция одной перемен-
ной
L
, (
−
L
затраты труда) и т. д.
3. Производная функции
(
)
xfy
=
в точке
x
()
(
)
(
)
x
xf
dx
xdf
dx
dy
xfy
x
∆
∆
===
′
=
′
→∆ 0
lim
трактуется как мгновенный прирост или мгновенная скорость изменения
зависимой переменной
y
(функции
(
)
xf ) в точке
x
. В экономической
теории производную принято называть предельной или маргинальной ха-
рактеристикой и использовать для неё следующие обозначения:
(
)
(
)
xfyxMfMy
′
=
′
=
=
.
Например, предельная выручка
(
)
=
qMR
()
(
)
dq
qdR
qR =
′
, предельные
издержки
=
MС
()
(
)
dq
QdC
QC =
′
, предельный продукт труда
() ()
(
)
dL
Ldf
LQLMQ =
′
= (часто обозначают MP
L
=MQ).
4. Относительное изменение (относительный прирост) аргу-
мента и соответствующее относительное изменение (относительный
прирост) зависимой переменной
y
(функции
(
)
xf )
x
x
∆
и
=
∆
y
y
(
)
()
xf
xf
∆
являются безразмерными величинами, показывающими, какую часть
x
∆
и
(
)
xfy
∆
=
∆
составляют от исходных значений
x
и
(
)
xfy
=
соответствен-
но. Умноженные на 100%, они дают изменения аргумента и функции, вы-
раженные в процентах.
5. Величина =
∆
∆
x
yy
(
)
(
)
x
xfxf
∆
∆
- темп прироста зависимой пере-
менной
y
(функции
(
)
xf ) при изменении аргумента от значения
x
до
x
x
∆
+
. Темп прироста равен средней скорости относительного изменения
функции при указанном изменении аргумента.
6. Величина
() ( )
y
dx
d
y
y
dx
dy
yx
yy
xr
x
ln
1
lim
0
=
′
=⋅=
∆
∆
=
→∆
или
()
()
(
)
(
)
()
()( )
xf
dx
d
xf
xf
dx
xdf
xf
xr ln
1
=
′
=⋅=
