Никифорова И.А. Математика в экономике: сборник задач. Часть ?
Подождите немного. Документ загружается.

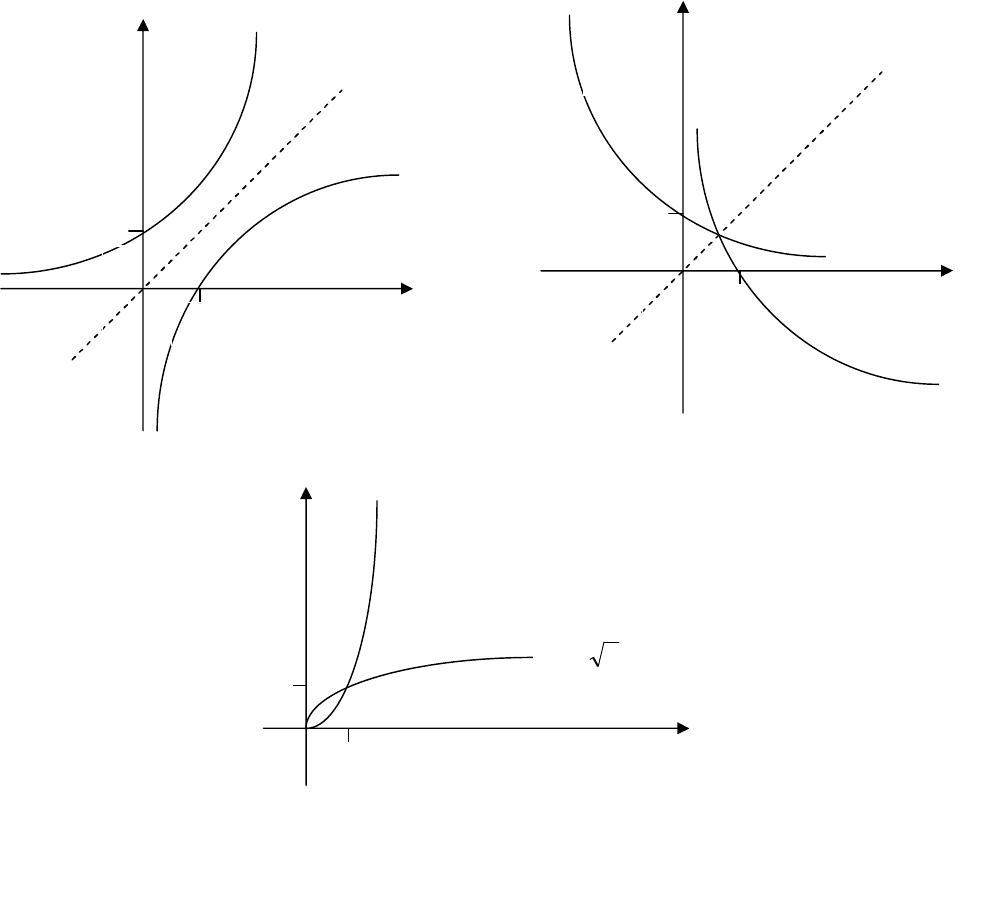
31
(
)
xfy
=
. (2.1)
Если для каждого
Y
y
∈
множество
(
)
yf
1−
состоит из одного элемен-
та, то обратная функция является однозначной, обычной в смысле введён-
ного нами выше определения функции одной переменной, с областью оп-
ределения Y и множеством значений
X
. В дальнейшем под обратными
будем понимать только однозначные функции. Графики исходной
(
)
xfy
=
и обратной функции
(
)
yfx
1−
= совпадают. Если для обратной функции
применить привычные обозначения зависимой переменной y и независи-
мой x, то график функции
(
)
xfy
1−
= получается путем отображения графи-
ка исходной функции
(
)
xfy
=
относительно биссектрисы первого и
третьего координатных углов.
Очевидно, что если для функции
(
)
xfy
=
существует обратная
(
)
yf
1−
, то обратная к последней существует и совпадает с исходной функ-
цией
(
)
xf , т.е.
(
)
(
)
(
)
xfyf =
−
−
1
1
.
1
1
y
x
0
а)
1
>
a
xy
a
log=
1
1
y
x
0
б)
1
0
<
<
a
xy
a
log=
x
ay =
x
ay =
0
1
1
y
x
xy =
2
xy =
в)
Рис. 2.1
32
Рассмотрим примеры. Обратной к показательной функции
x
ay = ,
1
,
0
≠
>
a
a
(
)
(
)
∞
+
=
=
,0, YRX является функция yx
a
log
=
(или в тради-
ционных обозначениях зависимой и независимой переменных xy
a
log
=
).
Обратной к функции
2
xy = ,
[
)
∞
+
∈
,0x является функция yx = (или в
традиционных обозначениях зависимой и независимой переменных
xy = ). Напомним, что графики функций
x
ay = и xy
a
log
=
;
2
xy = и
xy = при
[
)
∞
+
∈
,0x симметричны относительно биссектрисы первого и
третьего координатных углов (см. рис.2.1).
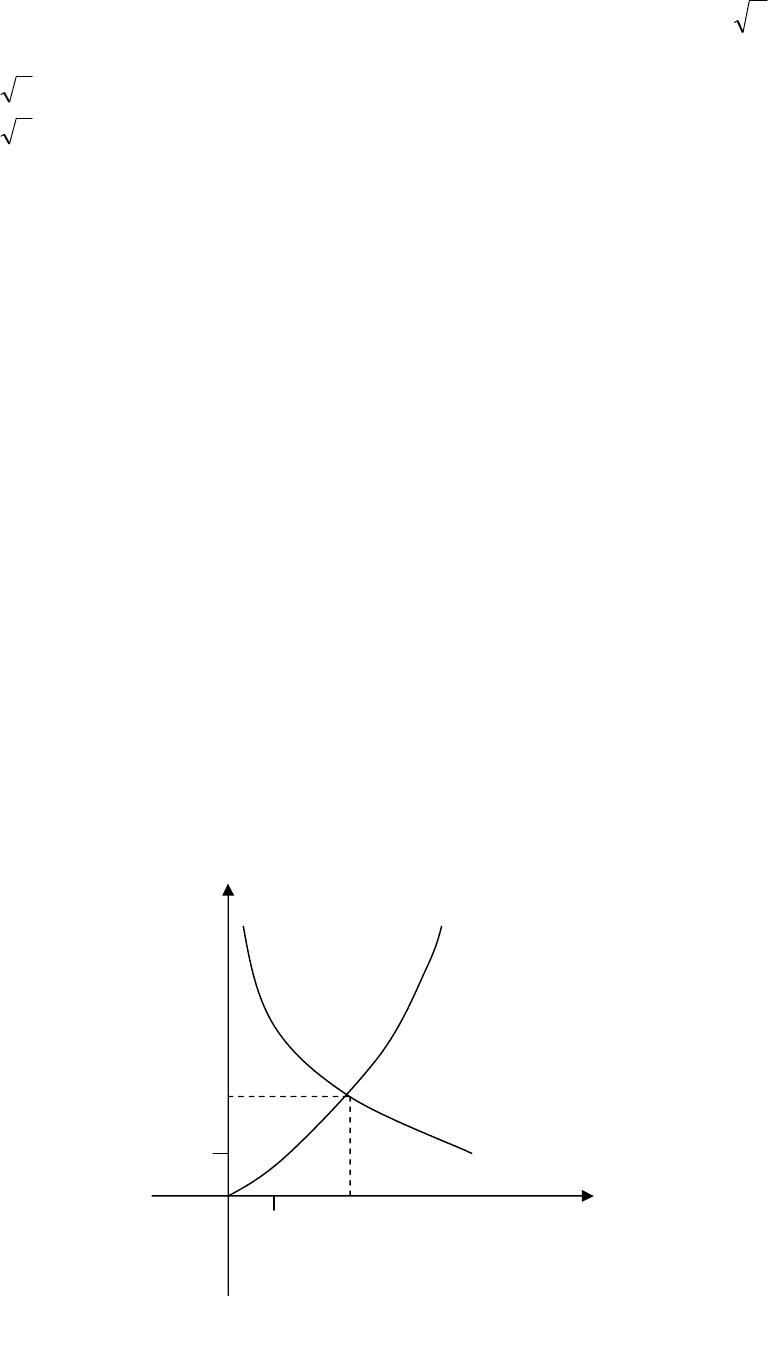
Если же мы будем рассматривать графики пары взаимно обратных
функций, например, показательной и логарифмической, не изменяя обо-
значений переменных обратной функции, то графики обеих функций сов-
падают, они представлены одной кривой
x
ay=
(
)
yx
a
log
=
, но для обрат-
ной функции yx
a
log
=
независимая переменная откладывается на верти-
кальной оси, а значение функции − на горизонтальной.
Это замечание важно для понимания некоторых графиков, исполь-
зуемых в экономической теории. В экономической теории, например, часто
используют функции, обратные функциям спроса
(
)
PfQ
d
= и предложения
(
)
PgQ
s
= от цены товара: ими являются соответственно функция цены от
спроса
(
)
d
QfP
1−
= и функция цены от предложения товара
(
)
s
QgP
1−
= .
График функции спроса
(
)
PfQ
d
= и обратной ей
(
)
d
QfP
1−
= называют
кривой спроса. График функции предложения
(
)
PgQ
s
= и обратной ей
(
)
s
QgP
1−
= называют кривой предложения.
Очевидно, что функция
(
)
PD монотонно убывает (как и
(
)
QD
1−
), а
функция
(
)
PS монотонно возрастает (как и
(
)
QS
1−
). При изображении гра-
фиков принято на вертикальной координатной оси откладывать цену
P
, а
на горизонтальной − спрос
Q
. Изобразим схематично кривые спроса и
предложения в одной координатной плоскости, см. рис. 2.2.
P
∗
P
1
1
*
Q
Q
0
(
)
(
)
(
)
QDPPDQ
1−
==
(
)
(
)
(
)
QSPPSQ
1−
==
Рис. 2.2

33
Точка пересечения кривых спроса и предложения есть точка равно-
весия спроса и предложения на рынке данного товара (точка рыночного
равновесия). Её координаты
(
)
**
,QP удовлетворяют условиям:
(
)
(
)
*1*1*
QDQSP
−−
== ,
(
)
(
)
***
PDPSQ == , где
−
*
P
равновесная цена,
*
Q −
равновесный объём. Для нахождения точки равновесия достаточно, напри-
мер, найти равновесную цену из равенства
(
)
(
)
**
PDPS = , а далее вычислить
равновесный объём:
(
)
**
PSQ = (или
(
)
**
PDQ = ).
Пример 2.2. При моделировании рынка некоторого товара на основе
статистических данных построены линейные функции спроса
P
Q
2
23
−
=
и
предложения
2
+
=
P
Q
.
1) Найти функции, обратные функциям спроса и предложения, их
области определения и множества значений.
2) Изобразить кривые спроса и предложения, вычислить точку ры-
ночного равновесия.
Решение. Область определения функции спроса
P
Q
2
23
−
=
задаётся
следующими условиями:
2
23
0
0223
,0
0
,0
≤≤⇔
≥−
≥
⇔
≥
≥
p
p
p
D
p
или
∈
2
1
11;0p
.
Т.о., областью её определения является отрезок
2
1
11;0
. Функция
является линейной и монотонно убывающей, поскольку коэффициент при
независимой переменной
P
отрицательный. Очевидно, что множество её
значений − отрезок
()
=
0;
2
1
11 QQ
[
]
23;0 . Разрешая уравнение
P
Q
2
23
−
=
относительно
P
, найдём функцию цены спроса QP
2
1
2
1
11 −= ,
область её определения − отрезок
[
]
23;0 , множество значений − отрезок
2
1
11;0
.
Обратной к функции предложения
2
+
=
P
Q
, очевидно, является
функция цены предложения
2
−
=
Q
P
с областью определения
[
)
∞
+
,2 (т.е.
∈
Q
[
)
∞
+
,2 ) и множеством значения
[
)
∞
+
,0 (т.е.
∈
P
[
)
∞
+
,0 ).
Изобразим кривые спроса и предложения на одной координатной
плоскости (см. рис. 2.3).

34
Из условия
P
P
2
23
2
−
=
+
найдём равновесную цену
7
*
=
P
, тогда
равновесный объём 92
**
=+= PQ .
Итак, функция цены от спроса QP
2
1
2
1
11 −= ,
[
]
23;0
∈
Q ,
∈
2
1
11;0P
;
функция цены от предложения товара
2
−
=
Q
P
,
[
)
∞
+
∈
,2Q ,
∈
P
[
)
∞
+
,0 ;
точка равновесия
(
)
(
)
7,9,
**
=PQ .
2.17. Найти обратные функции и области их определения, если ис-
ходные функции определены следующим образом:
1)
,
b
ax
y
+
=
−
b
a
,
параметры,
0
≠
a
;
2)
(
)
3
1−= xy ;
3)
,
sin
x
y
=
22
π
π
≤
≤
x ;
4) ,6
2
+= xy a)
0
≤
<
∞
−
x
; б)
+∞
<
≤
x
0
;
5) ,
x
ey =
6)
x
y
2
ln
=
;
7)
2
2
x
y = ;
8)
x
x
y
+
−
=
1
1
.
2.18. Кривые рыночного спроса заданы уравнениями:
1) PQ
20
1
5−= ; 2) 1
100
−=
P
Q , где
−
P
цена,
−
Q
объём спроса на данный
товар. Определить функцию цены от спроса на товар, построить её график
и график функции спроса от цены товара.
2.19. Кривая рыночного предложения задана уравнением:
1)
15
3
+
=
Q
P
; 2)
100
2
50
−
+=
Q
P
, где
−
P
цена,
−
Q
объём предложения
товара. Определить функцию предложения от цены товара, построить её
график и график функции цены от предложения товара.
Q
Рис.2.3
0 1
0
Q 23
−=−= QPPQ
2
1
2
1
11223
(
)
22 −=+= QPPQ
P
1
2
1
11
0
P

35
2.2. Предел функции. Непрерывность функции
1. Предел функции, основные определения. Пусть функция
(
)
xf ,
X
x
∈
, определена в некоторой окрестности точки
a
кроме, быть мо-
жет, самой точки
a
.
Число
A
называют пределом функции
(
)
xf при
x
, стремящемся к
a
(или в точке
a
), и обозначают
(
)
xfA
ax→
=
lim или
(
)
Axf
→
при
a
x
→
:
1) (определение на языке последовательностей) если для любой по-
следовательности значений аргумента
{
}
Xx
n
⊂
, ax
n
≠
, сходящейся к точке
a
, соответствующая последовательность
(
)
{
}
n
xf значений функции сходит-
ся к
A
;
2) (определение на языке «ε−δ»), если для любого, сколь угодно ма-
лого, числа 0
>
ε
найдётся такое число
(
)
εδδ =
0
>
, что для всех
a
x
≠
и
удовлетворяющих условию
δ
<
−
ax , выполняется неравенство
(
)
ε
<
−
Axf .
Оба приведённые определения предела функции в точке эквивалент-
ны.
Число
A
называют пределом функции
(
)
xf при
x
, стремящемся к
бесконечности, и обозначают
(
)
xfA
x ∞→
=
lim , если для любой бесконечно
большой последовательности
{
}
Xx
n
⊂
, соответствующая последователь-
ность значений функции
(
)
{
}
n
xf сходится к
A
или, если для любого числа
0
>
ε
найдётся такое число
(
)
εСС = 0
>
, что для всех
x
, удовлетворяющих
условию Cx
>
, выполнится неравенство
(
)
ε
<
−
Axf .
Если
a
x
<
и
a
x
→
, то пишут
0
−
→
a
x
, аналогично, если
a
x
>
и
a
x
→
, то пишут
0
+
→
a
x
. Если существуют
(
)
(
)
xfaf
ax 0
lim0
−→
=
−
и
(
)
(
)
0lim0
0
+
=
+
−→
xfaf
ax
, то числа
(
)
0
−
af и
(
)
0
+
af называют соответствен-
но левым пределом (или пределом слева) и правым пределом (или пределом
справа) функции
(
)
xf в точке a. Оба таких предела называют односто-
ронними. Аналогично определяются односторонние пределы функции при
−∞
→
x
и
+∞
→
x
, т.е.
(
)
xf
x ∞−→
lim и
(
)
xf
x ∞+→
lim .
Функция
(
)
xf имеет предел в точке
a
тогда и только тогда, когда в
этой точке существуют пределы справа и слева, совпадающие между со-
бой:
(
)
=
−
0af
(
)
0
+
af . В этом случае предел функции равен односторон-
ним пределам.
Пример 2.1. Используя определение, доказать, что
(
)
.1153lim
2
=
+
→
x
x
36
Решение. Возьмём произвольное
0
>
ε
. Для доказательства требуется
найти такое
0
>
δ
, при котором из неравенства
δ
<
−
2x следовало бы, что
(
)
=
−
11xf
(
)
ε
<
−
+
1153x . Преобразуем последнее неравенство, получим
ε
<
−
63x или
3
2
ε
<−x . Тогда при любом
3
ε
δ ≤ из неравенства
δ
<
−
2x
вытекает
(
)
ε
<
−
+
1153x . Это означает по определению, что
(
)
.1153lim
2
=
+
→
x
x
2.20. Используя определение, доказать, что:
1)
(
)
712lim
3
=
+
→
x
x
; 2)
(
)
1053lim
5
=
−
→
x
x
;
3) 1coslim
0
=
→
x
x
;
4) 0
1
sinlim
0
=
→
x
x
x
;
5) 0lim
0
=
→
x
x
;
6) 2
1
1
lim
1
=
−
−
→
x
x
x
.
2. Предел функции, основные свойства. Непрерывные функции.
Бесконечно малые и бесконечно большие функции. Неопределенности.
Пусть
−
C
постоянная и существуют
(
)
xf
ax→
lim и
(
)
xg
ax→
lim , тогда сущест-
вуют
1) СС
ax
=
→
lim ; 2)
(
)
⋅
=
⋅
→
СxfС
ax
lim
(
)
xf
ax→
lim ;
3)
(
)
(
)
(
)
=
±
→
xgxf
ax
lim
(
)
±
→
xf
ax
lim
(
)
xg
ax→
lim ;
4)
(
)
(
)
(
)
=
⋅
→
xgxf
ax
lim
(
)
⋅
→
xf
ax
lim
(
)
xg
ax→
lim ;
5)
(
)
(
)
(
)
=
→
xgxf
ax
lim
(
)
(
)
xgxf
axax →→
limlim (при
(
)
0lim
≠
→
xg
ax
).
Аналогичные свойства верны и для односторонних пределов и для
пределов при
∞
→
x
,
+∞
→
x
,
−∞
→
x
.
Если функция
(
)
xfy
=
определена в некоторой окрестности точки
a
,
и существует
(
)
(
)
afxf
ax
=
→
lim , то функцию
(
)
xfy
=
называют непрерывной
в точке
a
.
Если выполнено равенство
(
)
(
)
afxf
ax
=
−→ 0
lim
() ()
=
+→
afxf
ax 0
lim
, то
говорят, что функция
(
)
xfy
=
непрерывна в точке
a
слева (справа).
Сумма, произведение конечного числа функций, непрерывных в
точке
a
, есть функция, непрерывная в этой точке. Частное от деления двух
функций, непрерывных в точке
a
, есть функция, непрерывная в этой точке
при условии, что делитель отличен от нуля. Если функция
(
)
x
ϕ
непрерыв-
на в точке
a
, а функция
(
)
zf непрерывна в точке
(
)
ab
ϕ
=
, то сложная
функция
(
)
(
)
xf
ϕ
непрерывна в точке
a
.
Функцию
(
)
xfy
=
называют непрерывной на интервале
(
)
ba, , если
она непрерывна в каждой точке этого интервала; функцию
(
)
xfy
=
назы-

37
вают непрерывной на отрезке
[
]
ba, , если она непрерывна на интерва-
ле
(
)
ba, и непрерывна в точке
a
справа, а в точке
b
слева.
Любая из элементарных функций непрерывна в области своего опре-
деления.
В простейшем случае, когда функция, стоящая под знаком предела
(
)
xf
ax→
lim , непрерывна в точке
a
x
=
, вычисление предела сводится к под-
счёту значения
(
)
af . В других случаях нахождение предела требует специ-
альных исследований.
Функцию
(
)
xα называют бесконечно малой в точке
a
, если существу-
ет
(
)
0lim
=
→
x
ax
α
.
Функцию
(
)
xf называют бесконечно большой в точке
a
, если для
любой
{
}
Xx
n
⊂
, ax
n
≠
, x
n
→
a
последовательность
(
)
{
}
n
xf является беско-
нечно большой или, если для любого числа 0
>
M найдётся такое число
(
)
M
δ
δ
=
0
>
, что для всех
a
x
≠
и удовлетворяющих условию
δ
<
−
ax ,
выполняется неравенство
(
)
Mxf
>
. В этом случае пишут:
(
)
∞
=
→
xf
ax
lim .
По аналогии определяют бесконечно малые и бесконечно большие
функции при
∞
→
x
,
0
−
→
a
x
,
0
+
→
a
x
. Свойства бесконечно малых и
бесконечно больших функций аналогичны свойствам соответствующих по-
следовательностей. Например, если в точке
a
функция
(
)
x
α
является бес-
конечно малой и
(
)
0
≠
a
α
, то функция
()
xα
1
является бесконечно большой
в точке
a
. Если в точке
a
функция
(
)
xf является бесконечно большой, то
функция
()
xf
1
является бесконечно малой в этой точке.
Выражения вида
0
0
,
∞
∞
,
∞
−
∞
∞
⋅
,
0
,
0
,0,1 ∞
∞∞
используют для обо-
значения неопределенностей, возникающих при вычислениях пределов.
Условная запись
0
0
означает, например, что функция под знаком предела
равна отношению двух бесконечно малых, а
∞
∞
− отношению двух беско-
нечно больших величин и т. д. При наличии неопределённости функцию
под знаком предела следует преобразовать.
Пример 2.2. Вычислить:
1)
32
1
lim
2
3
++
−
∞−→
xx
x
x
;
2)
12
14
lim
2
2
+
+−
→
x
xx
x
; 3)
642
9
lim
2
2
3
−−
−
→
xx
x
x
;
4)
131
lim
0
−+
→
x
x
x
;
5)
( )
x
x
x
a
−∞→
∞+→
lim (
−
>
1
a
параметр);

38
Решение. 1) Имеем неопределённость
∞
∞
. Разделим числитель и зна-
менатель дроби на старшую степень
x
, имеющуюся в примере, т.е. на
3
x
:
=
++
−
∞−→
32
1
lim
2
3
xx
x
x
=
++
−
∞−→
32
3
321
11
lim
xxx
x
x
( )
−∞=
++
−
∞−→
2
3
3211
11
lim
xxx
x
x
.
При
∞
−
→
x
числитель дроби стремится к 1, а знаменатель дроби яв-
ляется бесконечно малым, причём 01
<
x . Следовательно, дробь является
бесконечно большой знака минус.
2) Подставляя предельное значение
2
=
x
в функцию, получим
5
3
122
1242
12
14
lim
22
2
−=
+⋅
+⋅−
=
+
+−
→
x
xx
x
.
3) Имеем неопределённость
0
0
. Выделим в числителе и знаменателе
дроби множитель
(
)
3
−
x , бесконечно малый при
3
→
x
:
=
−−
−
→
642
9
lim
2
2
3
xx
x
x
(
)
(
)
( )( )
=
+⋅−⋅
+
⋅
−
→
132
33
lim
3
xx
xx
x
(
)
( )
4
3
8
6
1
3
lim
2
1
3
==
+
+
⋅
→
x
x
x
.
4) Имеем неопределённость
0
0
. Умножим числитель и знаменатель
дроби на сумму
(
)
131 ++ x (выражение называют сопряжённым
к
(
)
131 −+ x ):
=
−+
→
131
lim
0
x
x
x
(
)
(
)
(
)
=
++⋅−+
++⋅
→
131131
131
lim
0
xx
xx
x
(
)
=
−+
++⋅
→
1
3
1
131
lim
0
x
xx
x
(
)
3
2
3
131
lim
0
=
++
→
x
x
.
5) )
x
x
a
∞+→
lim (
−
>
1
a
параметр);
(
)
1>= aay
x
x
y
Рис. 2.1
(
)
10 <<= aay
x
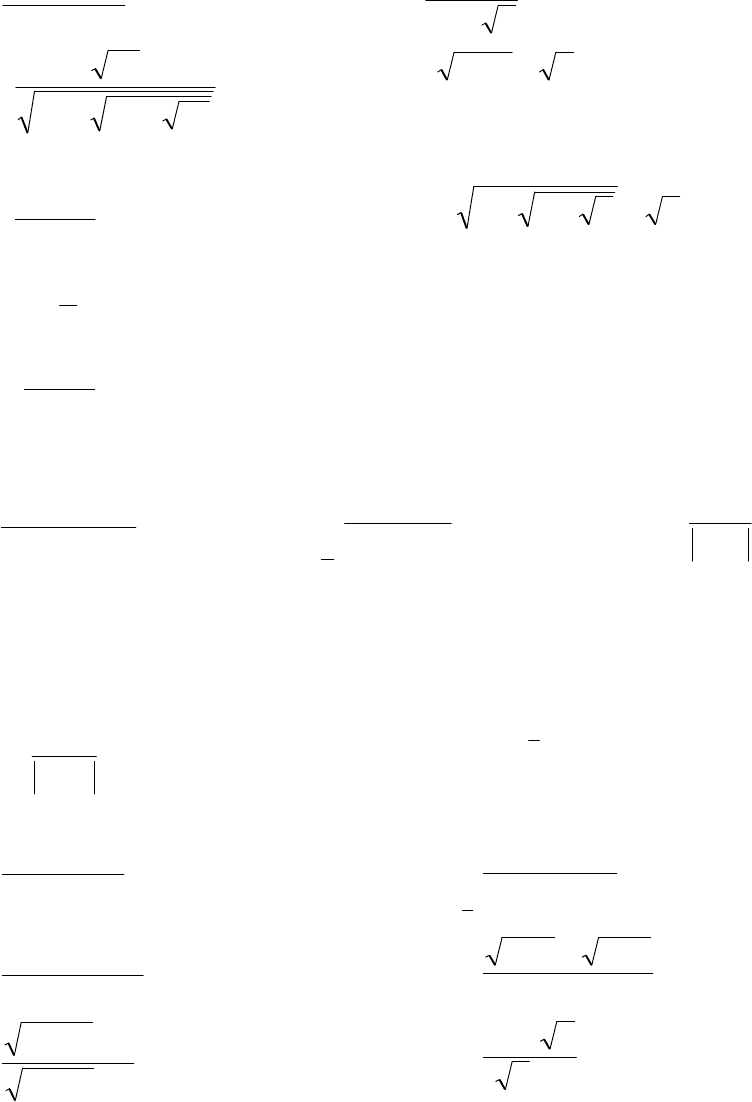
39
2.21. Вычислить пределы:
1)
13
5
lim
2
4
+−
−
∞→
xx
xx
x
;
2)
3
5
13
lim
xx
x
x
+
+
∞→
;
3)
xxx
x
x
333
2
lim
++
∞+→
;
4)
(
)
xax
x
−−
∞+→
lim (
−
a
пара-
метр);
5)
6
13
lim
2
−
+
∞−→
x
x
x
;
6)
−++
∞+→
xxxx
x
lim ;
7)
12
2
1lim
+
∞+→
+
x
x
x
;
8)
9)
( )
32
32
lim
−
+
−∞→
+∞→
x
x
x
x
;
10)
( )
arctgx
x
x
−∞→
∞+→
lim .
2.22. Вычислить пределы:
1)
153
2
lim
2
2
0
+−
−
→
xx
x
x
;
2)
x
x
x
2sin1
2cos1
lim
4
+
−
→
π
; 3)
3
lim
3
+
−→
x
x
x
.
2.23. Вычислить
(
)
xf
ax 0
lim
−→
,
(
)
xf
ax 0
lim
+→
, если:
1)
()
>−
≤
+
−
=
1,53
1,32
xx
xx
xf ,
1
=
a
;
2)
()
2
4
2
−
−
=
x
x
xf ,
2
=
a
;
3)
()
x
xf
1
2= ,
0
=
a
.
2.24. Установить вид неопределённости, вычислить пределы:
1)
xx
xx
x
−
+−
→
3
2
1
12
lim ; 2)
156
18
lim
2
3
2
1
+−
−
→
xx
x
x
;
3)
(
)
h
xhx
h
3
3
0
lim
−+
→
;
4)
x
xx
x
−−+
→
11
lim
0
;
5)
39
24
lim
2
2
0
−+
−+
→
x
x
x
;
6)
1
lim
2
1
−
−
→
x
xx
x
;
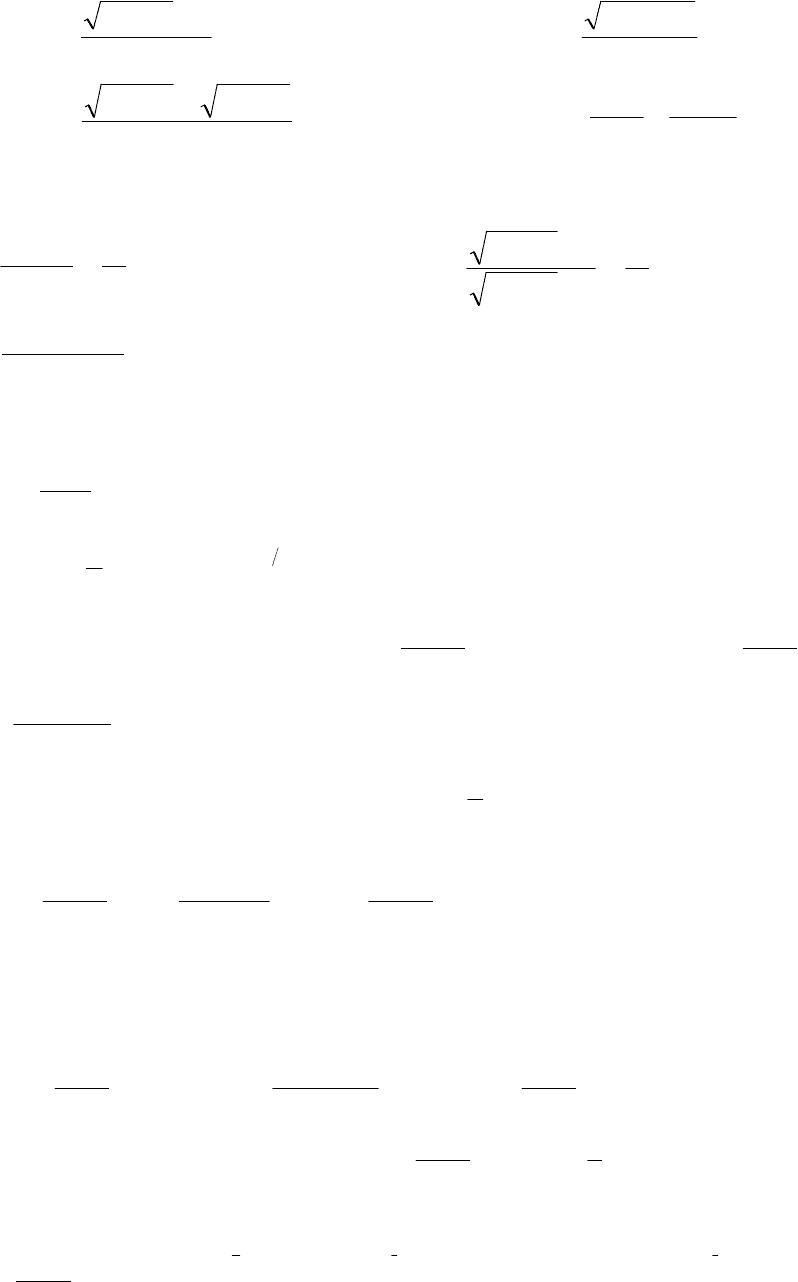
40
7)
x
mx
x
11
lim
3
0
−+
→
; 8)
x
x
x
sin
cos1
lim
0
+
+→π
;
9)
x
tgxtgx
x
2sin
11
lim
+−−
→π
;
10)
−
−
−
→
1
2
1
1
lim
2
1
x
x
x
.
2.25. Доказать следующие соотношения:
1)
n
m
x
x
n
m
x
=
−
−
→
1
1
lim
1
(
)
Nmn
∈
, ;
2)
(
)
( )
m
n
x
x
n
m
x
=
−+
−+
→
11
11
lim
0
(
)
Nmn
∈
, ;
3)
(
)
a
x
x
a
x
=
−+
→
11
lim
0
(
)
+
∈
Qa .
3. Замечательные пределы. Известны следующие пределы:
1
sin
lim
0
=
→
x
x
x
(первый замечательный предел);
=
+
∞→
x
x
x
1
1lim
(
)
e=+
→
α
α
α
1
0
1lim (второй замечательный предел).
Пример 2.3. Вычислить:1)
x
x
x
4sin
lim
0→
; 2)
x
x
x
x
+
−
∞→
2
1
lim ;
3)
(
)
x
x
x
2
31ln
lim
0
+
+→
.
Решение. 1) Имеем неопределённость
0
0
. Умножим числитель и зна-
менатель дроби на 4 и воспользуемся первым замечательным пределом:
=
→
x
x
x
4sin
lim
0
=
⋅
→
x
x
x
4
4sin4
lim
0
414
4
4sin
lim4
0
=⋅=⋅
→
x
x
x
.
2) Убедившись, что имеет место неопределённость
∞
1
, преобразуем
выражение, стоящее под знаком предела, выделим в основании слагаемое,
равное 1:
=
+
−
∞→
x
x
x
x
2
1
lim
=
∞
1
(
)
=
+
−+
∞→
x
x
x
x
2
32
lim
x
x
x
+
−
+
∞→
2
3
1lim .
Введём новую переменную ⇒
+
−=
2
3
x
t 2
3
−−=
t
x и
0
→
t
при
∞
→
x
. Продолжим вычисление предела в новой переменной:
=
+
−
+
∞→
x
x
x 2
3
1lim
( )
=+
−−
→
2
3
1lim
0
t
t
t
( )
( )
⋅+
−⋅
→
3
1
1lim
0
t
t
t
( )
=+
−
→
2
1lim
0
t
t
( )
=⋅
+
−
→
11lim
3
0
1
t
t
t
3−
e
.
3) Имеем:
