Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 1

Подождите немного. Документ загружается.

221

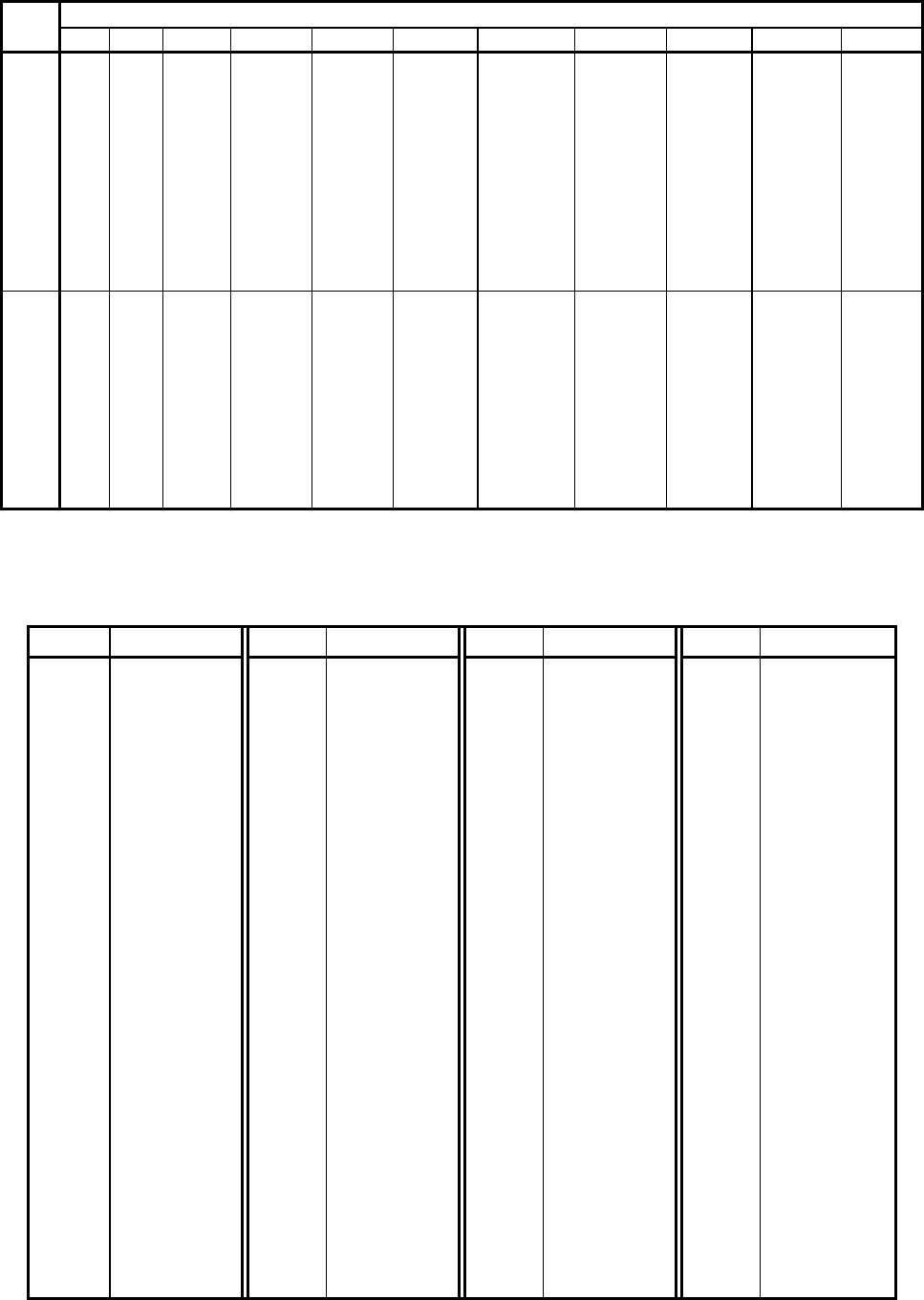
Òàáëèöà I.9

Б ИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ

n m

1 2 3 4 5 6 7 8 9 10

0 1

1 1

2 1

3 1

3 3 1

4 1

4 6 4 1

5 1

5 10 10 5 1

6 1

6 15 20 15 6 1

7 1

7 21 35 35 21 7 1

8 1

8 28 56 70 56 28 8 1

9 1

9 36 84 126 126 84 36 9 1

45 120 210 252 210 120 45 10 1

55 165 330 462 462 330 165 55 11

66 220 495 792 924 792 495 220 66

78 286 715 1287

1716 1716 1287

715 286

91 364 1001

2002

3003 3432 3003

2002

1001

105

455 1365

3003

5005 6435 6435

5005

3003

120

560 1820

4368

8008 11440

12870

11440

8008

136

680 2380

6188

12376

19448

24310

19448

153

816 3060

8568

18564

31824

43758

48620

43758

171

969 3876

11628

27132

50388

75582

92378

190

1140

4845

15504

38760

77520

125970

167960

184756

Òàáëèöà I.10

Г АММА-ФУНКЦИЯ

() ( )

Ãx t tdt

= -

exp

x Ã(x) x Ã(x) x Ã(x) x Ã(x)

1,00

1,000000

1,25

0,906402

10,50

0,886227

1,75

0,919063

1,01

0,994326

1,26

0,904397

1,51

0,886592

1,76

0,921375

1,02

0,988844

1,27

0,902503

1,52

0,887039

1,77

0,923763

1,03

0,983550

1,28

0,900718

1,53

0,887568

1,78

0,926227

1,04

0,978438

1,29

0,899042

1,54

0,888178

1,79

0,928767

1,05

0,973504

1,30

0,897471

1,55

0,888868

1,80

0,931384

1,06

0,968744

1,31

0,896004

1,56

0,889639

1,81

0,934076

1,07

0,964152

1,32

0,894640

1,57

0,890490

1,82

0,936845

1,08

0,959725

1,33

0,893378

1,58

0,891420

1,83

0,939690

1,09

0,955459

1,34

0,892216

1,59

0,892428

1,84

0,942612

1,10

0,951351

1,35

0,891151

1,60

0,893515

1,85

0,945611

1,11

0,947396

1,36

0,890185

1,61

0,894681

1,86

0,948687

1,12

0,943590

1,37

0,889314

1,62

0,895924

1,87

0,951840

1,13

0,939931

1,38

0,888537

1,63

0,897244

1,88

0,955071

1,14

0,936416

1,39

0,887854

1,64

0,898642

1,89

0,958379

1,15

0,933041

1,40

0,887264

1,65

0,900117

1,90

0,961766

1,16

0,929803

1,41

0,886765

1,66

0,901668

1,91

0,965231

1,17

0,926700

1,42

0,886356

1,67

0,903296

1,92

0,968774

1,18

0,923728

1,43

0,886036

1,68

0,905001

1,93

0,972397

1,19

0,920885

1,44

0,885805

1,69

0,906782

1,94

0,976099

1,20

0,918169

1,45

0,885661

1,70

0,908639

1,95

0,979881

1,21

0,915576

1,46

0,885604

1,71

0,910572

1,96

0,983743

1,22

0,913106

1,47

0,885633

1,72

0,912581

1,97

0,987685

1,23

0,910755

1,48

0,885747

1,73

0,914665

1,98

0,991708

1,24

0,908521

1,49

0,885945

1,74

0,916826

1,99

0,995813

1,25

0,906402

1,50

0,886227

1,75

0,919063

2,00

1,000000

Äëÿ x<1 (x¹0,-1,-2,...) Ã(x) = Ã(x+1)/x, äëÿ x>2 Ã(x) = (x-1)Ã(x-1)

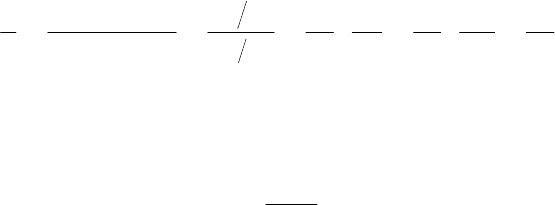
222

Приложение II

Вероятностные координатные сетки

Îñíîâíîé ïðèíöèï ãðàôè÷åñêîãî ìåòîäà ïîäáîðà âèäà ðàñïðåäåëåíèÿ è îïðåäåëåíèÿ

åãî ïàðàìåòðîâ ñîñòîèò â âûáîðå òàêîé ñèñòåìû êîîðäèíàò, â êîòîðîé ãðàôèê ôóíêöèè

ðàñïðåäåëåíèÿ F(t) ñëó÷àéíîé âåëè÷èíû t ñòàíîâèòñÿ ïðÿìîé ëèíèåé. Íà âåðîÿòíîñò-

íîé áóìàãå â ïðÿìîóãîëüíîé ñèñòåìå êîîðäèíàò ïî îñè îðäèíàò íàíîñèòñÿ øêàëà, ñîîò-

âåòñòâóþùàÿ èíòåãðàëüíîé ôóíêöèè çàêîíà ðàñïðåäåëåíèÿ F(t), à ïî îñè àáñöèññ - ëè-

íåéíàÿ t èëè ëîãàðèôìè÷åñêàÿ øêàëà lnt.

Äëÿ êàæäîãî çàêîíà ðàñïðåäåëåíèÿ ñóùåñòâóþò ñâîè ïðåîáðàçîâàíèÿ êîîðäèíàò,

îáðàùàþùèå ãðàôèê èíòåãðàëüíîé ôóíêöèè F(t) â ïðÿìóþ ëèíèþ. Äëÿ ýêñïîíåíöèàëü-

íîãî è íîðìàëüíîãî çàêîíîâ ïðåîáðàçóåòñÿ ìàñøòàá òîëüêî ïî âåðòèêàëüíîé îñè, ïî îñè

àðãóìåíòà îí îñòàåòñÿ ëèíåéíûì. Äëÿ ëîãàðèôìè÷åñêè íîðìàëüíîãî çàêîíà è ðàñïðåäå-

ëåíèÿ Âåéáóëëà ìàñøòàáû ïî îáåèì îñÿì íåëèíåéíû (ïî îñè àðãóìåíòà øêàëà ëîãà-

ðèôìè÷åñêàÿ). Òèï ñåòêè, íà êîòîðîé ýêñïåðèìåíòàëüíûå òî÷êè ðàñïîëàãàþòñÿ îêîëî

ïðÿìîé ëèíèè íàèáîëåå òî÷íî, óêàçûâàåò íà íàèëó÷øèé àïïðîêñèìèðóþùèé òåîðåòè÷å-

ñêèé çàêîí.

Âåðîÿòíîñòíûå êîîðäèíàòíûå ñåòêè (âåðîÿòíîñòíûå áóìàãè) èñïîëüçóþòñÿ êàê äëÿ

ïðîâåðêè ñîãëàñèÿ ýìïèðè÷åñêîãî ðàñïðåäåëåíèÿ ñ òåîðåòè÷åñêèì (â ýòîì ñëó÷àå ïîëó-

÷åííûå ðåçóëüòàòû èñïûòàíèé â âèäå òî÷åê ðàñïîëàãàþòñÿ âäîëü ïðÿìîé ëèíèè), òàê è

äëÿ îöåíêè ïàðàìåòðîâ ðàñïðåäåëåíèÿ (ïî óãëó íàêëîíà ïðÿìîé è îòðåçêàì, êîòîðûå

îíà îòñåêàåò íà îñÿõ êîîðäèíàò).

Ýêñïîíåíöèàëüíîå ðàñïðåäåëåíèå. Ïîñëå ëîãàðèôìèðîâàíèÿ ôóíêöèè ýêñïîíåíöè-

àëüíîãî ðàñïðåäåëåíèÿ (2.72)

F(t) = exp(-lt) (II.1)

ìîæíî ïîëó÷èòü óðàâíåíèå ïðÿìîé â âèäå

y = -ln[1-F(t)] = lt. (II.2)

Ïðè ïîñòðîåíèè âåðîÿòíîñòíîé êîîðäèíàòíîé ñåòêè äëÿ ýêñïîíåíöèàëüíîãî çàêîíà

ðàñïðåäåëåíèÿ ïî îñè àáñöèññ ñòðîèòñÿ ðàâíîìåðíàÿ øêàëà x=t, ïî îñè îðäèíàò - çíà-

÷åíèå ëîãàðèôìè÷åñêîé ôóíêöèè y = -ln[1-F(t)] (íåðàâíîìåðíàÿ ëîãàðèôìè÷åñêàÿ

øêàëà). Çíà÷åíèÿ x íà îñè àáñöèññ ìîæíî îòêëàäûâàòü ïðè ïîìîùè ñîîòíîøåíèÿ

t (ãäå k

= L

- ìàñøòàáíûé ôàêòîð, L

- äëèíà îñè, ìì, R

= t

max

-t

min

- ðàç-

ìàõ âàðüèðîâàíèÿ).

Åñëè ïðèíÿòü ìèíèìàëüíîå çíà÷åíèå ôóíêöèè F(t)=0 è ìàêñèìàëüíîå çíà÷åíèå

F(t)=0,99, òî íàèìåíüøåå çíà÷åíèå ôóíêöèè y

min

=-ln[1-F(t)]=-ln(1)=0, íàèáîëüøåå

max

= -ln[1-F(t)] = -ln(1-0,99) = 4,6052 è äëÿ ïîñòðîåíèÿ îñè îðäèíàò ìîæíî âîñ-

ïîëüçîâàòüñÿ ñîîòíîøåíèåì S

= k

y =

ln[1-F(t)] (ãäå k

= L

/(y

max

-y

min

) =

/4,6052 = 0,2171L

- ìàñøòàáíûé ôàêòîð, L

- äëèíà îñè, ìì).

Ñõåìà ïîñòðîåíèÿ ãðàôèêà ýêñïîíåíöèàëüíîãî ðàñïðåäåëåíèÿ ïîêàçàíà íà ðèñ.II.1.

Äëÿ îïðåäåëåíèÿ çíà÷åíèÿ ïàðàìåòðà ðàñïðåäåëåíèÿ l ìîæíî âîñïîëüçîâàòüñÿ

óðàâíåíèåì (II.2), èç êîòîðîãî ñëåäóåò (ðèñ.II.1)

(

)

[

]

l j= =

- -

= = × = × =

y y

x x

ln 1

, (II.3)

ãäå j - óãîë ìåæäó ëèíèåé ãðàôèêà è îñüþ àáñöèññ.

Íîðìàëüíîå ðàñïðåäåëåíèå. Ôóíêöèþ íîðìàëüíîãî ðàñïðåäåëåíèÿ âèäà (2.78)

t = m + u

s (II.4)

ìîæíî ïðåäñòàâèòü â âèäå óðàâíåíèÿ ïðÿìîé

, (II.5)

ãäå u

- êâàíòèëü íîðìàëüíîãî ðàñïðåäåëåíèÿ óðîâíÿ p = F(t), m=M(t) è s - ïàðàìåòðû

ðàñïðåäåëåíèÿ (ìàòåìàòè÷åñêîå îæèäàíèå è ñðåäíåå êâàäðàòè÷åñêîå îòêëîíåíèå).

Äëÿ ïîñòðîåíèÿ íà îñè àáñöèññ îòêëàäûâàåòñÿ ðàâíîìåðíàÿ øêàëà äëÿ àðãóìåíòà

x=t, à ïî îñè îðäèíàò - çíà÷åíèÿ êâàíòèëè íîðìàëüíîãî ðàñïðåäåëåíèÿ y=u

è íàäïè-

ñûâàåòñÿ ñîîòâåòñòâóþùàÿ åé âåëè÷èíà F(t). Çíà÷åíèÿ x íà îñè àáñöèññ ìîæíî îòêëà-

äûâàòü ïðè ïîìîùè ñîîòíîøåíèÿ S

= k

t (ãäå k

- ìàñøòàáíûé ôàêòîð, L

äëèíà îñè, ìì, R

= t

max

-t

min

- ðàçìàõ âàðüèðîâàíèÿ).

Äëÿ ïîñòðîåíèÿ øêàëû ôóíêöèè ðàñïðåäåëåíèÿ F(t) çàäàþòñÿ, êàê ïðàâèëî, èíòåð-

âàëîì îò F

min

=0,01 äî F

max

=0,99 (èíîãäà îò F

min

=0,001 äî F

max

=0,999). Òîãäà ïî òàá-

223

ëèöàì u

(ñì.ïðèë.I) y

max

0,99

=2,3263 è y

min

0,01

= -2,3263 (ò.ê. u

=-u

1-p

). Èíòåðâàë

âàðüèðîâàíèÿ R

= y

max

min

= 4,6526 è äëÿ ïîñòðîåíèÿ îñè îðäèíàò ìîæíî âîñïîëüçî-

âàòüñÿ ñîîòíîøåíèåì S

(ãäå k

= L

- ìàñøòàáíûé ôàêòîð, L

- äëèíà îñè,

ìì). Ïðè F(t)<0,5 ìîæíî âîñïîëüçîâàòüñÿ ñîîòíîøåíèåì u

=-u

1-F

Íà ðèñ.II.2 ïîêàçàíà ñõåìà ïîñòðîåíèÿ ãðàôèêà ôóíêöèè íîðìàëüíîãî ðàñïðåäåëå-

íèÿ â âåðîÿòíîñòíûõ êîîðäèíàòàõ.

Òàê êàê ïðè F(t)=0,5 y=u

0,5

=0, òî ïî óðàâíåíèþ (II.5) t=m, ò.å. ïðÿìàÿ ïåðåñåêàåò

îñü àáñöèññ â òî÷êå x=m. Äëÿ îïðåäåëåíèÿ çíà÷åíèÿ s ìîæíî òàêæå âîñïîëüçîâàòüñÿ

óðàâíåíèåì (II.5), èç êîòîðîãî ñëåäóåò (ðèñ.II.2)

m m

= ×

= × =

S k

ODOB

ctg

x x

y y

x x

, (II.6)

ãäå j - óãîë ìåæäó ëèíèåé ãðàôèêà è îñüþ àáñöèññ.

Èç óðàâíåíèÿ (II.6) ñëåäóåò, ÷òî ïðè x=t=0 y=u

=-m/s è äëÿ îïðåäåëåíèÿ ïàðà-

ìåòðà s ìîæíî òàêæå èñïîëüçîâàòü çíà÷åíèå îðäèíàòû òî÷êè ïåðåñå÷åíèÿ ãðàôèêà ñ

îñüþ y:

m=- =

. (II.7)

Ëîãàðèôìè÷åñêè íîðìàëüíîå ðàñïðåäåëåíèå. Ïîñëå ïðåîáðàçîâàíèÿ ôóíêöèè ëî-

ãàðèôìè÷åñêè íîðìàëüíîãî ðàñïðåäåëåíèÿ â âèäå

lnt = m +u

s (II.8)

ìîæíî ïîëó÷èòü óðàâíåíèå ïðÿìîé â âèäå

, (II.9)

ãäå u

- êâàíòèëü íîðìàëüíîãî ðàñïðåäåëåíèÿ óðîâíÿ p = F(t); m=M(lnt) è s - ïàðàìåò-

ðû ðàñïðåäåëåíèÿ (ìàòåìàòè÷åñêîå îæèäàíèå è ñðåäíåå êâàäðàòè÷åñêîå îòêëîíåíèå ëî-

ãàðèôìà ñëó÷àéíîé âåëè÷èíû).

Âåðîÿòíîñòíàÿ êîîðäèíàòíàÿ ñåòêà ñòðîèòñÿ àíàëîãè÷íî íîðìàëüíîìó ðàñïðåäåëå-

íèþ, íî íà îñè àáñöèññ îòêëàäûâàþòñÿ çíà÷åíèÿ ëîãàðèôìà ñëó÷àéíîé âåëè÷èíû x=lnt

ïî óðàâíåíèþ S

= k

lnt (ãäå k

= L

/(lnt

max

lnt

min

) - ìàñøòàáíûé ôàêòîð, L

- äëèíà

îñè, ìì). Î÷åâèäíî, ïðè ïîñòðîåíèè ìîæíî ëîãàðèôìèðîâàòü çíà÷åíèÿ ñëó÷àéíîé âå-

ëè÷èíû ïî ëþáîìó îñíîâàíèþ, ïðè èñïîëüçîâàíèè äåñÿòè÷íîãî ëîãàðèôìà: lgt =

0,43429×lnt è lnt = 2,30259×lnt.

Ïî îñè îðäèíàò îòêëàäûâàþòñÿ çíà÷åíèÿ êâàíòèëè íîðìàëüíîãî ðàñïðåäåëåíèÿ

y=u

è íàäïèñûâàåòñÿ ñîîòâåòñòâóþùàÿ åé âåëè÷èíà F(t). Äëÿ ïîñòðîåíèÿ øêàëû F(t)

ôóíêöèè ðàñïðåäåëåíèÿ çàäàþòñÿ, êàê ïðàâèëî, èíòåðâàëîì îò F

min

=0,01 äî F

max

=0,99

x=t

F(t)

0,99

max

0,01

j=arcctgs

0,5

x=m

x=t

F(t)

]

0,99

max

j=arctgl

min

y=-m/s

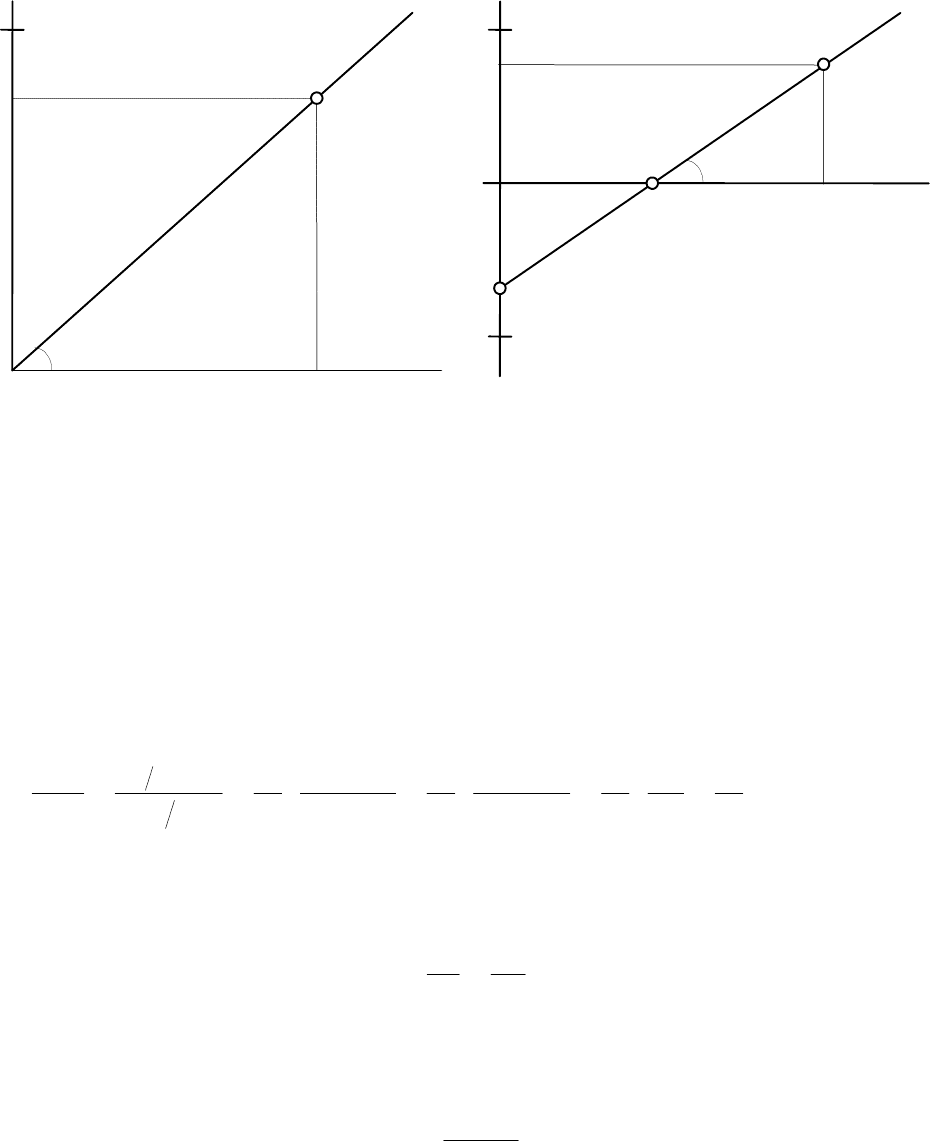
Ðèñ.II.1. Ñõåìà ïîñòðîåíèÿ ãðàôèêà Ðèñ.II.2. Ñõåìà ïîñòðîåíèÿ ãðàôèêà

ôóíêöèè ýêñïîíåíöèàëüíîãî ðàñïðåäåëåíèÿ ôóíêöèè íîðìàëüíîãî ðàñïðåäåëåíèÿ

â âåðîÿòíîñòíûõ êîîðäèíàòàõ â âåðîÿòíîñòíûõ êîîðäèíàòàõ

224

(èíîãäà îò F

min

=0,001 äî F

max

=0,999). Òîãäà ïî òàáëèöàì u

(ñì.ïðèë.I)

max

0,99

=2,3263 è y

min

0,01

=-2,3263 (ò.ê. u

=-u

1-p

), ïîýòîìó èíòåðâàë âàðüèðîâàíèÿ

ïî îñè îðäèíàò R

= y

max

min

=4,6526 è äëÿ åå ïîñòðîåíèÿ ìîæíî âîñïîëüçîâàòüñÿ ñî-

îòíîøåíèåì S

(ãäå k

- ìàñøòàáíûé ôàêòîð, L

- äëèíà îñè, ìì). Ïðè

F(t)<0,5 ìîæíî òàêæå âîñïîëüçîâàòüñÿ ñîîòíîøåíèåì u

=-u

1-F

Íà ðèñ.II.3 ïîêàçàíà ñõåìà ïîñòðîåíèÿ ãðàôèêà ôóíêöèè ëîãàðèôìè÷åñêè íîðìàëü-

íîãî ðàñïðåäåëåíèÿ íà âåðîÿòíîñòíîé áóìàãå.

Äëÿ îïðåäåëåíèÿ ïàðàìåòðîâ ðàñïðåäåëåíèÿ m è s ìîæíî âîñïîëüçîâàòüñÿ êîîðäè-

íàòàìè òî÷åê ïåðåñå÷åíèÿ ïðÿìîé ñ îñÿìè êîîðäèíàò. Â òî÷êå ïåðåñå÷åíèÿ B ïðÿìîé

ëèíèè ñ îñüþ àáñöèññ lnt = m, ò.å. m=x

= OB/k

. Â òî÷êå ïåðåñå÷åíèÿ ïðÿìîé ñ îñüþ

îðäèíàò A x=lnt=0 è t=1, ò.å. OA=S

m/s, îòêóäà

j=- = = =

ctg

y y

, (II.10)

ãäå j - óãîë ìåæäó ëèíèåé ãðàôèêà è îñüþ àáñöèññ (ðèñ.II.3).

Ïîñëå îïðåäåëåíèÿ ïàðàìåòðîâ m è s ìîãóò áûòü âû÷èñëåíû õàðàêòåðèñòèêè ðàñ-

ïðåäåëåíèÿ (ìàòåìàòè÷åñêîå îæèäàíèå, äèñïåðñèÿ, êîýôôèöèåíò âàðèàöèè).

Ðàñïðåäåëåíèå Âåéáóëëà. Ïîñëå äâîéíîãî ëîãàðèôìèðîâàíèÿ ôóíêöèè ðàñïðåäåëå-

íèÿ Âåéáóëëà â âèäå (2.92)

F(x) = 1 - exp(-lx

), f(x) = alx

exp(-lx

). (II.11)

ìîæíî ïîëó÷èòü óðàâíåíèå â âèäå

y = ln{-ln[1-F(t)]} = aln(lt) = a(lnt+lnl) = 2,303×a(lgt+lgl). (II.12)

Èç óðàâíåíèÿ (II.12) ñëåäóåò, ÷òî âåëè÷èíà y=ln{-ln[1-F(t)]} ëèíåéíî çàâèñèò îò

ëîãàðèôìà ñëó÷àéíîé âåëè÷èíû x=lnt. Ïîýòîìó íà îñè àáñöèññ îòêëàäûâàåòñÿ ëîãà-

ðèôìè÷åñêàÿ øêàëà x=lnt ïî ñîîòíîøåíèþ S

lgt (ãäå k

/(lnt

max

lnt

min

) - ìàñ-

øòàáíûé ôàêòîð, L

- äëèíà îñè, ìì). Ïðè ïîñòðîåíèè ìîæíî ëîãàðèôìèðîâàòü çíà÷å-

íèÿ ñëó÷àéíîé âåëè÷èíû ïî ëþáîìó îñíîâàíèþ, ïðè èñïîëüçîâàíèè äåñÿòè÷íîãî ëîãà-

ðèôìà lgt = 0,43429×lnt è lnt = 2,30259×lgt. Íà îñè îðäèíàò îòêëàäûâàåòñÿ âåëè÷èíà

y=ln{-ln[1-F(t)]}, íî ïðîñòàâëÿåòñÿ ñîîòâåòñòâóþùåå çíà÷åíèå F(t). Äëÿ ïîñòðîåíèÿ

øêàëû F(t) çàäàþòñÿ èíòåðâàëîì îò F

min

=0,01 äî F

max

=0,99. Òîãäà ïî ôîðìóëå (II.12)

min

=ln{-ln[0,99]}=-4,6001 è y

max

=ln{-ln[0,01]}=1,5272, ïîýòîìó èíòåðâàë âàðüèðîâà-

íèÿ ïî îñè îðäèíàò R

max

min

=6,1273 è äëÿ åå ïîñòðîåíèÿ ìîæíî âîñïîëüçîâàòüñÿ

ñîîòíîøåíèåì S

y=ln{-ln[1-F(t)]} (ãäå k

- ìàñøòàáíûé ôàêòîð, L

- äëèíà

îñè, ìì). Ïî óðàâíåíèþ (II.12) ìîæíî ïîëó÷èòü, ÷òî ïðè F(t)=0,6321 y=0 è S

=0.

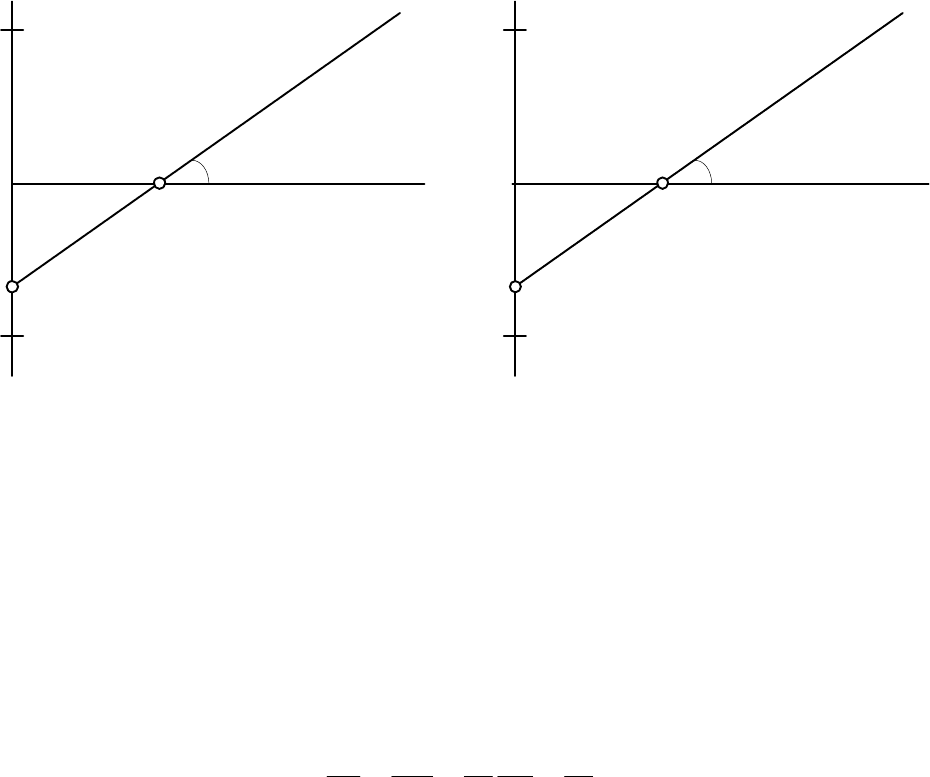
Ñõåìà ïîñòðîåíèÿ ãðàôèêà ôóíêöèè ðàñïðåäåëåíèÿ Âåéáóëëà ïîêàçàíà íà ðèñ.II.4.

Èç óðàâíåíèÿ (II.12) ñëåäóåò, ÷òî y = 0 ïðè lnt=-lnl è, ñîîòâåòñòâåííî, l=1/t.

Ïîýòîìó âåëè÷èíó ïàðàìåòðà l ìîæíî íàéòè ïî êîîðäèíàòå òî÷êè ïåðåñå÷åíèÿ ïðÿìîé

ñ îñüþ àáñöèññ (ðèñ.II.4) è ôîðìóëå (II.12): OB=k

lnl, lnl=OB/k

(ãäå OB=S

- ðàñ-

ñòîÿíèå îò íà÷àëà êîîðäèíàò äî òî÷êè B ïåðåñå÷åíèÿ ãðàôèêà ñ îñüþ àáñöèññ, ìì).

x=lnt

F(t)

[1-

F(t)

]}

0,99

0,01

0,6321

x=lnt

F(t)y=u

0,99

0,01

x = m

=-m/s

=(lnt-m)/s

x=0

t=1

y=alnl

Ðèñ.II.3. Ñõåìà ïîñòðîåíèÿ ãðàôèêà ôóíêöèè Ðèñ.II.4. Ñõåìà ïîñòðîåíèÿ ãðàôèêà

ëîãàðèôìè÷åñêè íîðìàëüíîãî ðàñïðåäåëåíèÿ ôóíêöèè ðàñïðåäåëåíèÿ Âåéáóëëà

â âåðîÿòíîñòíûõ êîîðäèíàòàõ â âåðîÿòíîñòíûõ êîîðäèíàòàõ

225

Äëÿ íàõîæäåíèÿ çíà÷åíèÿ âòîðîãî ïàðàìåòðà ðàñïðåäåëåíèÿ a ïðåäïîëîæèì, ÷òî â

óðàâíåíèè (II.12) t=1 è, ñîîòâåòñòâåííî, x=0. Òîãäà y

= alnl. Òàê êàê OA=k

, òî

l l

j= = = =

ln lg

, (II.13)

ãäå j - óãîë ìåæäó ëèíèåé ãðàôèêà è îñüþ àáñöèññ (ðèñ.II.4).

Òàê êàê ïðè èñïîëüçîâàíèè ãðàôè÷åñêîãî ìåòîäà äëÿ ëþáîãî ðàñïðåäåëåíèÿ ãðàôèê

ôóíêöèè ïðèîáðåòàåò âèä ïðÿìîé, òî êîýôôèöèåíòû àïïðîêñèìèðóþùåãî ëèíåéíîãî

óðàâíåíèÿ y = ax+b äëÿ åå òî÷íîãî ïðîâåäåíèÿ è îïðåäåëåíèÿ êîîðäèíàò òî÷åê ïåðåñå-

÷åíèÿ ñ îñÿìè ìîãóò áûòü íàéäåíû ìåòîäîì (ñïîñîáîì) íàèìåíüøèõ êâàäðàòîâ

(ïðèë.III), ïðè ýòîì x

è y

- àáñöèññà è îðäèíàòà ýêñïåðèìåíòàëüíûõ òî÷åê â ïðåîáðà-

çîâàííûõ (âåðîÿòíîñòíûõ) îñÿõ êîîðäèíàò (i=1,2,...,n): äëÿ ýêñïîíåíöèàëüíîãî ðàñïðå-

äåëåíèÿ x

, y

=ln[1-F*(t

)], äëÿ íîðìàëüíîãî x

, y

*, äëÿ ëîãàðèôìè÷åñêè

íîðìàëüíîãî x

=lnt

, y

*, äëÿ ðàñïðåäåëåíèÿ Âåéáóëëà x

=lnt

, y=ln{-ln[1-F*(t

)]}.

Òîãäà êîîðäèíàòû òî÷åê ïåðåñå÷åíèÿ ñ îñÿìè êîîðäèíàò, óãîë íàêëîíà ïðÿìîé è,

ñîîòâåòñòâåííî, ïàðàìåòðû ðàñïðåäåëåíèé ìîãóò áûòü ðàññ÷èòàíû íåïîñðåäñòâåííî ïî

ýêñïåðèìåíòàëüíûì äàííûì è ôîðìóëàì ïðèë.III, ÷òî ïîçâîëÿåò èñêëþ÷èòü ïîãðåøíî-

ñòè ãåîìåòðè÷åñêèõ ïîñòðîåíèé:

- àáñöèññà òî÷êè ïåðåñå÷åíèÿ ïðÿìîé ñ îñüþ x (y=0): x

= -b/a;

- îðäèíàòà òî÷êè ïåðåñå÷åíèÿ ïðÿìîé ñ îñüþ y (x=0): y

= b;

- óãîë ìåæäó ïðÿìîé è ãîðèçîíòàëüíîé îñüþ: j = arctg(a).

Òîãäà äëÿ ýêñïîíåíöèàëüíîãî ðàñïðåäåëåíèÿ (ðèñ.II.1);

l = tgj = a, (II.14)

äëÿ íîðìàëüíîãî è ëîãàðèôìè÷åñêè íîðìàëüíîãî ðàñïðåäåëåíèé (ðèñ.II.2 è II.3)

m = x

= -b/a, s = ctgj = 1/tgj = 1/a, (II.15)

äëÿ ðàñïðåäåëåíèÿ Âåéáóëëà (ðèñ.II.4)

l = exp(-x

) = exp(b/a), a = y

/lnl = a. (II.15)

Ïðèìåð. Ïî ýêñïåðèìåíòàëüíûì äàííûì î íàðàáîòêå 50 èçäåëèé (òàáë.II.1) ïîä-

òâåðäèòü ïðàâèëüíîñòü âûáîðà íîðìàëüíîãî çàêîíà è îïðåäåëèòü çíà÷åíèÿ ïàðàìåòðîâ

ôóíêöèè ðàñïðåäåëåíèÿ (â òàáëèöå i - íîìåð çíà÷åíèÿ âàðèàöèîííîãî ðÿäà, t

- çíà÷å-

Òàáëèöà II.1

РЕЗУЛЬТАТЫ ИСПЫТАНИЙ И ОЦЕНКА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

F*(t

)

ìì

F*(t

)

ìì

31,22

0,02 -2,054

1,4

-33,1

103,30

0,52 0,050

84,6

0,8

34,79

0,04 -1,751

5,5

-28,2

104,24

0,54 0,100

85,7

1,6

40,85

0,06 -1,555

12,5

-25,1

104,60

0,56 0,151

86,1

2,4

42,65

0,08 -1,405

14,6

-22,7

106,04

0,58 0,202

87,7

3,3

52,10

0,10 -1,282

25,5

-20,7

108,01

0,60 0,253

90,0

4,1

54,11

0,12 -1,175

27,8

-18,9

108,29

0,62 0,305

90,3

4,9

60,75

0,14 -1,080

35,5

-17,4

108,59

0,64 0,358

90,7

5,8

67,48

0,16 -0,994

43,2

-16,0

109,38

0,66 0,412

91,6

6,6

67,82

0,18 -0,915

43,6

-14,8

110,63

0,68 0,468

93,0

7,5

68,24

0,20 -0,842

44,1

-13,6

111,75

0,70 0,524

94,3

8,5

69,80

0,22 -0,772

45,9

-12,4

111,90

0,72 0,583

94,5

9,4

82,85

0,24 -0,706

61,0

-11,4

116,14

0,74 0,643

99,4

10,4

83,75

0,26 -0,643

62,0

-10,4

116,76

0,76 0,706

100,1

11,4

85,05

0,28 -0,583

63,5

-9,4

118,77

0,78 0,772

102,4

12,4

85,47

0,30 -0,524

64,0

-8,5

119,48

0,80 0,842

103,2

13,6

85,59

0,32 -0,468

64,1

-7,5

126,54

0,82 0,915

111,4

14,8

87,39

0,34 -0,412

66,2

-6,6

126,94

0,84 0,994

111,9

16,0

92,47

0,36 -0,358

72,1

-5,8

128,15

0,86 1,080

113,3

17,4

95,05

0,38 -0,305

75,1

-4,9

131,91

0,88 1,175

117,6

18,9

97,64

0,40 -0,253

78,0

-4,1

133,10

0,90 1,282

119,0

20,7

97,80

0,42 -0,202

78,2

-3,3

134,97

0,92 1,405

121,1

22,7

98,46

0,44 -0,151

79,0

-2,4

137,12

0,94 1,555

123,6

25,1

99,06

0,46 -0,100

79,7

-1,6

155,94

0,96 1,751

145,3

28,2

101,51

0,48 -0,050

82,5

-0,8

157,30

0,98 2,054

146,9

33,1

101,80

0,50 0,000

82,9

0,0

169,71

1,00 161,2

226

íèå âàðèàöèîííîãî ðÿäà - çíà÷åíèå ñëó÷àéíîé íàðàáîòêè, F*(t

) - íàêîïëåííàÿ ÷àñòîòà -

ýêñïåðèìåíòàëüíîå çíà÷åíèå ôóíêöèè ðàñïðåäåëåíèÿ, u

* - êâàíòèëü ðàñïðåäåëåíèÿ,

ñîîòâåòñòâóþùàÿ çíà÷åíèþ F*, S

è S

- êîîðäèíàòû òî÷åê â âåðîÿòíîñòíîì ìàñøòàáå).

Äëÿ ïîñòðîåíèÿ âûáèðàåì äëèíû îñåé L

=150 ìì è L

=75 ìì. Ìàñøòàáíûå ôàêòî-

ðû ïî îñÿì k

= L

=150/130=1,154 è k

=75/4,6526=16,12. Êîîðäèíàòû òî-

÷åê îïðåäåëÿþòñÿ ïî ôîðìóëàì S

= k

(t-30)=1,154×(t-30) è S

=16,12×u

(íà÷àëî

êîîðäèíàò S

= 0 è S

= 0 ðàçìåùåíî â òî÷êå t=30 ÷ è u

= 0). Çíà÷åíèÿ S

è S

äëÿ

âûáîðêè ïðèâåäåíû â òàáë.II.1.

Ïðè ïîñòðîåíèè ëèíèè ñåòêè ñòðîèòü íå îáÿçàòåëüíî, äîñòàòî÷íî ïîñòðîèòü n òî÷åê

ñ ñîîòâåòñòâóþùèìè êîîðäèíàòàìè â óêàçàííîì ìàñøòàáå.

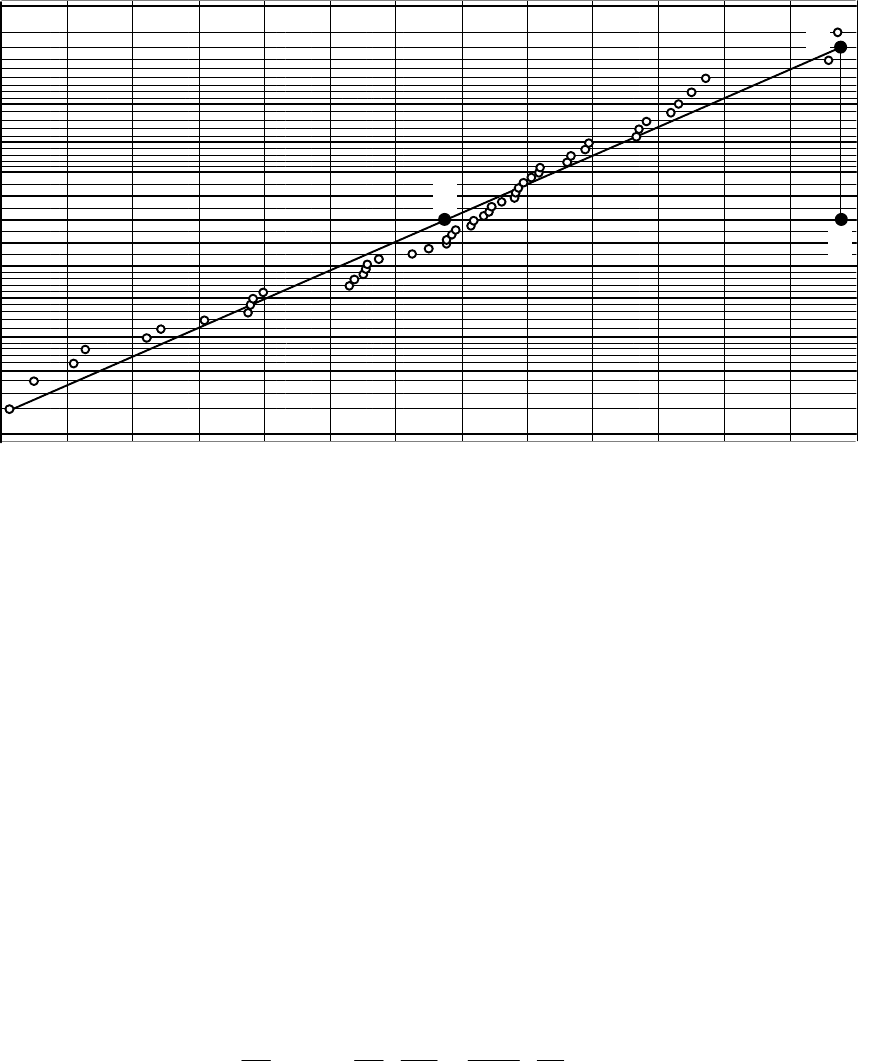
Ïîñòðîåíèå ïîêàçûâàåò (ðèñ.II.5), ÷òî â âåðîÿòíîñòíûõ êîîðäèíàòàõ äëÿ íîðìàëüíî-

ãî çàêîíà òî÷êè ðàñïîëàãàþòñÿ âäîëü ïðÿìîé ëèíèè, ÷òî ïîäòâåðæäàåò ïðàâèëüíîñòü

âûáîðà çàêîíà ðàñïðåäåëåíèÿ.

Ïàðàìåòðû íîðìàëüíîãî ðàñïðåäåëåíèÿ ìîæíî îïðåäåëèòü ïî ïîñòðîåííîé ïðÿìîé.

Àáñöèññà åå ïåðåñå÷åíèÿ ñ ãîðèçîíòàëüíîé îñüþ S

ñîîòâåòñòâóåò çíà÷åíèþ ìàòåìàòè-

÷åñêîãî îæèäàíèÿ ñëó÷àéíîé âåëè÷èíû m. Èç ãðàôèêà S

» 77 ìì, îòêóäà m » S

+30

= 77/1,154+30 » 97 ÷. Âòîðîé ïàðàìåòð ôóíêöèè ðàñïðåäåëåíèÿ (ñðåäíåå êâàäðàòè÷å-

ñêîå îòêëîíåíèå) ìîæíî îïðåäåëèòü ïî ôîðìóëå (II.6):

s j= = × = × »

ctg

1612

1154

315

ãäå B - òî÷êà ïåðåñå÷åíèÿ ïðÿìîé ñ ãîðèçîíòàëüíîé îñüþ, C - ïðîèçâîëüíàÿ òî÷êà íà

ïðÿìîé (ïî âîçìîæíîñòè - ìàêñèìàëüíî óäàëåííàÿ îò òî÷êè B), D - îñíîâàíèå ïåðïåí-

äèêóëÿðà, îïóùåííîãî èç òî÷êè C íà ãîðèçîíòàëüíóþ îñü.

Êîýôôèöèåíòû a è b àïïðîêñèìèðóþùåãî ëèíåéíîãî óðàâíåíèÿ y =ax+b ìîãóò áûòü

íàéäåíû ïî ôîðìóëàì ìåòîäà íàèìåíüøèõ êâàäðàòîâ (ïðèë.III), â êîòîðûå äëÿ íîðìàëü-

íîãî ðàñïðåäåëåíèÿ ïîäñòàâëÿþòñÿ çíà÷åíèÿ x

è y

*(t

). Ïîäñòàíîâêà çíà÷åíèé

äëÿ 50 òî÷åê (òàáë.II.1) äàåò a=0,0313 è b=-3,0499. Òîãäà ïî ôîðìóëàì (II.15)

m = -b/a = 3,0499/0,0313 = 97,44 ÷, s = 1/a = 1/0,0313 = 31,95 ÷.

Îêîí÷àòåëüíî ïðèíèìàåì m = 97,5 ÷ è s = 32,0 ÷.

Íà ðèñ.II.6-II.9 ïðèâåäåíû ïîëíîñòüþ ïîñòðîåííûå âåðîÿòíîñòíûå êîîðäèíàòíûå

ñåòêè äëÿ ýêñïîíåíöèàëüíîãî, íîðìàëüíîãî, ëîãàðèôìè÷åñêè íîðìàëüíîãî ðàñïðåäåëå-

íèé è ðàñïðåäåëåíèÿ Âåéáóëëà.

30 40 50 60 70 80 90 100 110 120 130 140 150

0,50

0,40

0,60

0,70

0,30

0,20

0,80

0,10

0,90

0,99

0,05

0,01

Ðèñ.II.5. Ïîñòðîåíèå ôóíêöèè ðàñïðåäåëåíèÿ ïî ýêñïåðèìåíòàëüíûì äàííûì

â âåðîÿòíîñòíûõ êîîðäèíàòàõ äëÿ íîðìàëüíîãî ðàñïðåäåëåíèÿ

(ê ïðèìåðó II.1)

227

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

0,50

0,90

0,95

0,99

Ðèñ.II.1. Êîîðäèíàòíàÿ ñåòêà äëÿ ýêñïîíåíöèàëüíîãî ðàñïðåäåëåíèÿ

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

0,50

0,40

0,30

0,20

0,10

0,05

0,01

0,60

0,80

0,70

0,90

0,95

0,99

Ðèñ.II.2. Êîîðäèíàòíàÿ ñåòêà äëÿ íîðìàëüíîãî ðàñïðåäåëåíèÿ

228

1 10 100

1000

0,01

0,10

0,20

0,30

0,40

0,50

0,60

0,70

0,80

0,90

0,99

2 5 20 50 200 500

Ðèñ.II.3. Êîîðäèíàòíàÿ ñåòêà äëÿ ëîãàðèôìè÷åñêè íîðìàëüíîãî ðàñïðåäåëåíèÿ

1 10 100 10002 5 20 50 200 500

0,01

0,05

0,10

0,20

0,30

0,40

0,50

0,60

0,70

0,80

0,90

0,99

0,95

Ðèñ.II.3. Êîîðäèíàòíàÿ ñåòêà äëÿ ðàñïðåäåëåíèÿ Âåéáóëëà

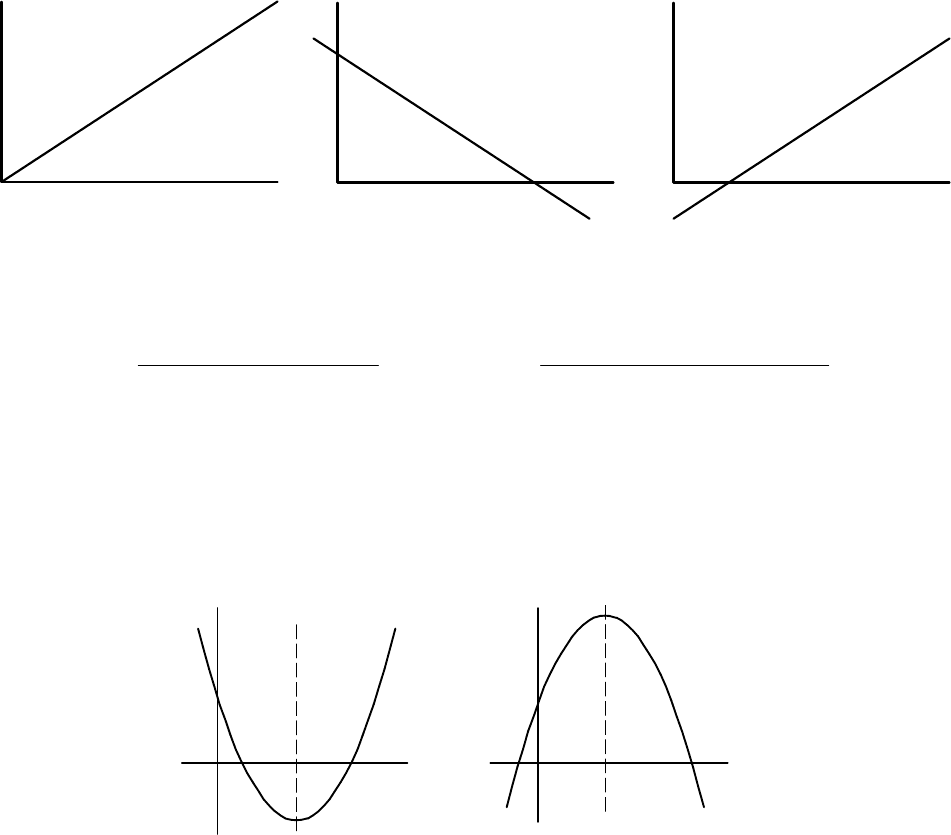
229

Приложение III

Определение эмпирических зависимостей

способом наименьших квадратов

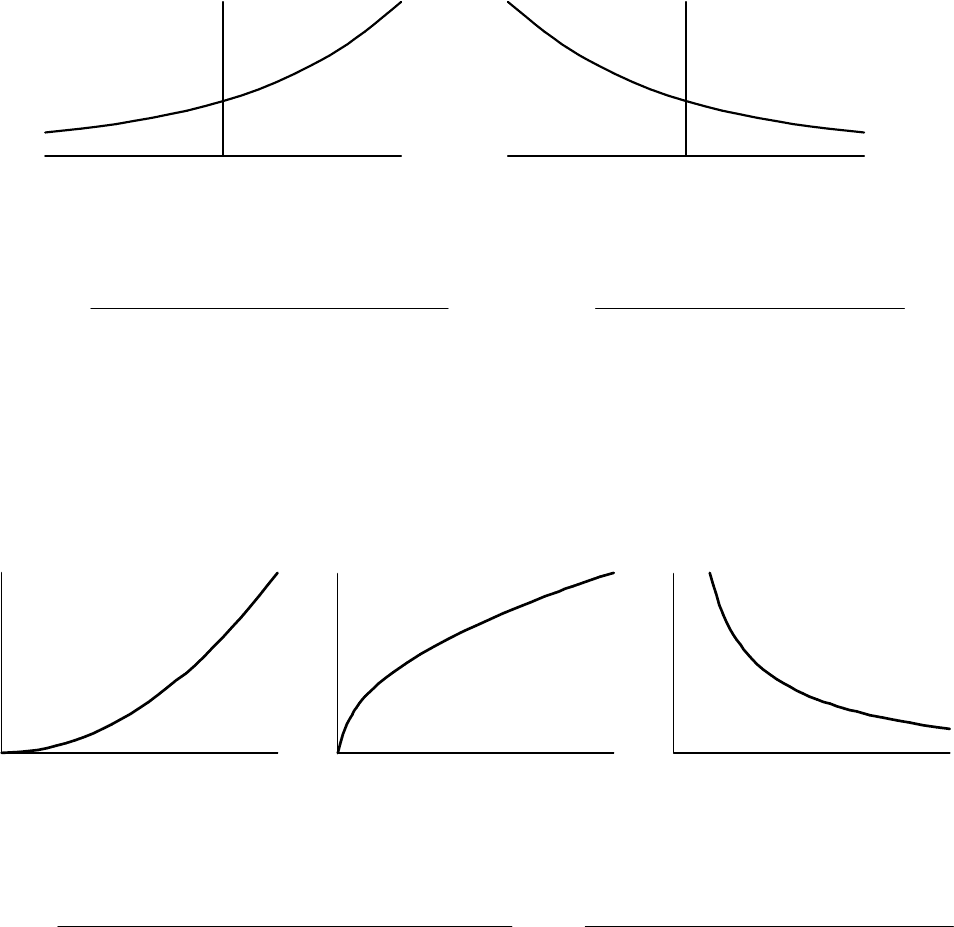
III.1. Функция y = ax + b

-b/a

n xy x y

n x x

y x x xy

n x x

= = =

= =

= = = =

= =

å åå

å å

åå åå

å å

1 1 1

1 1

1 1 1

1 1

;

III.2. Функция y = ax

+ bx + c

a x b x c x xy

a x b x cn y

i i

1 1 1

= = = =

= = =

å å å å

å å å

+ + =

230

III.3. Функция y = ab

или lgy = lga +xlgb

a a

lg lg

x y x x y

n x x

n x y x y

n x x

i i

= = = =

= =

= = =

= =

å å åå

å å

å åå

å å

1 1 1 1

1 1

1 1 1

1 1

;

III.4. Функция y = ax

или lgy = lga +blgx

lg lg lg lg lg

lg lg

lg lg lg lg

lg lg

y x x x y

n x x

n x y x y

n x x

i i

= = = =

= =

= = =

= =

å å å å

å å

å å å

å å

1 1 1

2 2

1 1

1 1 1

2 2

1 1

;