Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 1

Подождите немного. Документ загружается.

191

(

)

(

)

P q Q P q

i i

= - = - = - -

Õ Õ

1 1 1 1

. (5.75)

Åñëè

<<1 è â âûðàæåíèÿõ (5.75) ïîñëå ðàñêðûòèÿ ñêîáîê ïðåíåáðå÷ü âåëè÷èíàìè

ïîðÿäêà 2k

è âûøå, òî ìîæíî çàïèñàòü

P q Q q

i i

» - »

å å

(5.76)

(ïðèíÿòîå äîïóùåíèå íå âíåñåò ñóùåñòâåííîé ïîãðåøíîñòè â òî÷íîñòü ðàñ÷åòîâ ïðè

max{q

} << 1/n, ÷òî âûïîëíÿåòñÿ äîñòàòî÷íî ÷àñòî).

Åñëè ñòîèìîñòü ýëåìåíòà êàæäîé ãðóïïû îáîçíà÷èòü ÷åðåç c

, òî ñóììàðíàÿ ñòîè-

ìîñòü ñèñòåìû ïîñëå ðåçåðâèðîâàíèÿ

. (5.77)

Ôîðìóëèðîâêà ïðÿìîé çàäà÷è îïòèìèçàöèè (îáåñïå÷åíèå ìèíèìàëüíîé ñòîèìîñòè

ïðè çàäàííîé íàäåæíîñòè) ñâîäèòñÿ ê îïðåäåëåíèþ çíà÷åíèé k

(i=1,2,...,n)), îáåñïå÷è-

âàþùèõ ìèíèìàëüíîå çíà÷åíèå C(k

) ïðè çàäàííîì çíà÷åíèè P(k

) = P

èëè Q(k

) = Q

Äëÿ ðåøåíèÿ çàäà÷è ìåòîäîì íåîïðåäåëåííûõ ìíîæèòåëåé Ëàãðàíæà öåëåâóþ

ôóíêöèþ (ëàãðàíæèàí) çàïèøåì â âèäå

L(k

) = C(k

) + y[Q(k

) – Q

], (5.78)

ãäå y - íåîïðåäåëåííûé ìíîæèòåëü Ëàãðàíæà.

Ðåøåíèå çàäà÷è ñâîäèòñÿ ê ðåøåíèþ ñèñòåìû n+1 óðàâíåíèé ñ íåèçâåñòíûìè

,...,k

,y:

( )

k k

kc y q Q i n

q Q

i i

= + -

= =

å å

1 1

0 12, ,,...,,

(5.79)

Ïîñëå äèôôåðåíöèðîâàíèÿ ïåðâûõ n óðàâíåíèé ïîëó÷èì

c yq q

+ =ln 0

, (5.80)

îòêóäà

. (5.81)

Ïîñëå ïîäñòàíîâêè âûðàæåíèÿ (5.81) â ïîñëåäíåå óðàâíåíèå ñèñòåìû (5.79) ïîëó÷èì

- =

, (5.82)

îòêóäà

. (5.83)

Òîãäà óðàâíåíèå (5.81) ïðèîáðåòàåò âèä

, (5.84)

îòêóäà

( )

[ ]

q q

A h

i i

= -

+ -

= + -

1 1

ln ln

, (5.85)

ãäå

( )

= » - -

. 1

. (5.86)

Àíàëîãè÷íî ìîæíî ðåøèòü è îáðàòíóþ çàäà÷ó îïòèìèçàöèè.

192

Î÷åâèäíî ïîëó÷åííûå ðåçóëüòàòû íóæäàþòñÿ â

êîððåêòèðîâêå äî öåëî÷èñëåííûõ çíà÷åíèé k

, ÷òî

âíîñèò íåêîòîðóþ íåîäíîçíà÷íîñòü è ìíîãîâàðè-

àíòíîñòü îïòèìèçàöèè. Ïîýòîìó â öåëîì ïîëó÷åí-

íûå ðåøåíèÿ ìîãóò èñïîëüçîâàòüñÿ äëÿ îðèåíòèðî-

âî÷íûõ ðàñ÷åòîâ, äàæå åñëè äîïóùåíèå (5.76) ñî-

áëþäàåòñÿ íå î÷åíü ñòðîãî.

Äëÿ ñèñòåìû ñ ïîñëåäîâàòåëüíûì ñîåäèíåíèåì

äâóõ ýëåìåíòîâ ñ âåðîÿòíîñòÿìè îòêàçîâ â òå÷å-

íèå çàäàííîãî âðåìåíè q

= 0,3 è q

= 0,5 , ñòîè-

ìîñòüþ c

= 1 è c

= 3 (â óñëîâíûõ åäèíèöàõ) ðàñ-

÷åò ïî ôîðìóëàì (5.75) ïîêàçûâàåò, ÷òî áåç ðåçåð-

âèðîâàíèÿ âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû ñèñòå-

ìû P(1,1) = 0,35 è âåðîÿòíîñòü îòêàçà Q(1,1) = 0,65. Åñëè íåîáõîäèìî óâåëè÷èòü âåðî-

ÿòíîñòü áåçîòêàçíîé ðàáîòû ñèñòåìû äî P(k

) = P

= 0,98 (èëè ñíèçèòü âåðîÿòíîñòü

îòêàçà äî Q(k

) = Q

= 0,02 ) ïðè ìèíèìàëüíîé ñòîèìîñòè ñèñòåìû, òî ðàñ÷åò ïî

ôîðìóëàì (5.85)-(5.86) äàåò ñëåäóþùèå ðåçóëüòàòû: k

=4,77, k

=5,91. Äëÿ ïîëó÷åíèÿ

öåëî÷èñëåííîãî ðåøåíèÿ íåîáõîäèìî ðàññìîòðåòü ÷åòûðå âàðèàíòà ñî÷åòàíèé öåëûõ

çíà÷åíèé k

è k

, ïîëó÷àþùèõñÿ ïðè îêðóãëåíèè äî áëèæàéøèõ ìåíüøèõ è áîëüøèõ: 1)

= 4, k

= 5, C(4,5) = 19, Q(4,5) = 0,039 > Q

; 2) k

= 4, k

= 6, C(4,6) = 22, Q(4,6)

= 0,024 > Q

; 3) k

= 5, k

= 5, C(5,5) = 20, Q(5,5) = 0,034 > Q

; 4) k

= 5, k

= 6,

C(5,6) = 23, Q(5,6) = 0,018 < Q

. Èç ðàññìîòðåííûõ âàðèàíòîâ òîëüêî ÷åòâåðòûé ïîë-

íîñòüþ óäîâëåòâîðÿåò ïîñòàâëåííûì óñëîâèÿì çàäà÷è.

Ìåòîä íåîïðåäåëåííûõ ìíîæèòåëåé Ëàãðàíæà ïðè ðåøåíèè çàäà÷

ñòðóêòóðíîé îïòèìèçàöèè äîñòàòî÷íî ïðîñò è óäîáåí. Îäíàêî â áîëåå

ñëîæíûõ ñëó÷àÿõ (íàïðèìåð, ïðè íåíàãðóæåííîì èëè îáëåã÷åííîì ðåçåð-

âèðîâàíèè, ïðè íàëè÷èè íåñêîëüêèõ îãðàíè÷åíèé è ò.ä.) åãî èñïîëüçîâàíèå

íå âñåãäà ïîçâîëÿåò íàéòè àíàëèòè÷åñêîå ðåøåíèå è ïîýòîìó äëÿ ýòîãî

÷àñòî ïðèõîäèòñÿ èñïîëüçîâàòü ÷èñëåííûå ìåòîäû, èç-çà ÷åãî ïðåèìóùåñò-

âà ìåòîäà ìíîæèòåëåé Ëàãðàíæà òåðÿþòñÿ [37,41].

Â ýòèõ ñëó÷àÿõ ìîæåò áûòü öåëåñîîáðàçíî âîñïîëüçîâàòüñÿ ìåòîäîì

íàèñêîðåéøåãî ñïóñêà [33,36,38,42], õîðîøî ïðèñïîñîáëåííûì äëÿ íàõîæ-

äåíèÿ öåëî÷èñëåííûõ ðåøåíèé è èñïîëüçîâàíèþ ñðåäñòâ âû÷èñëèòåëüíîé

òåõíèêè.

Íàõîæäåíèå îïòèìàëüíîé ñòðóêòóðû ðåçåðâèðîâàííîé ñèñòåìû ïî ìå-

òîäó íàèñêîðåéøåãî ñïóñêà ïðåäñòàâëÿåò ñîáîé ìíîãîøàãîâûé ïðîöåññ, íà

êàæäîì øàãå êîòîðîãî äîáàâëÿåòñÿ ðåçåðâíûé ýëåìåíò, êîòîðûé îáåñïå÷èò

íàèáîëüøåå óäåëüíîå ïðèðàùåíèå íàäåæíîñòè â ðàñ÷åòå íà åäèíèöó çà-

òðàò. Ïðîöåññ ïðîäîëæàåòñÿ äî òåõ ïîð, ïîêà íå áóäåò äîñòèãíóòî òðåáóå-

ìîå çíà÷åíèå âåðîÿòíîñòè áåçîòêàçíîé ðàáîòû èëè äðóãîé õàðàêòåðèñòèêè

íàäåæíîñòè (ïðè ðåøåíèè ïðÿìîé çàäà÷è îïòèìèçàöèè), èëè íå áóäåò äîñ-

òèãíóòà ïðåäåëüíàÿ ñòîèìîñòü òåõíè÷åñêîé ñèñòåìû (ïðè ðåøåíèè îáðàò-

íîé çàäà÷è îïòèìèçàöèè). Â êà÷åñòâå íà÷àëüíîãî ìîæåò ðàññìàòðèâàòüñÿ

êàê èñõîäíîå ñîñòîÿíèå ñèñòåìû, òàê è êàêîå-ëèáî ïðèáëèæåííîå ê îïòè-

ìàëüíîìó, âûáðàííîå ïî äîïîëíèòåëüíûì ñîîáðàæåíèÿì èñõîäÿ èç êîí-

êðåòíûõ óñëîâèé çàäà÷è.

Ïðàêòè÷åñêè âûáîð ýëåìåíòà äëÿ ðåçåðâèðîâàíèÿ íà êàæäîì øàãå îï-

ðåäåëÿåòñÿ ìàêñèìàëüíûì çíà÷åíèåì óäåëüíîãî ïðèðàùåíèÿ íàäåæíîñòè

(íàïðèìåð, âåðîÿòíîñòè áåçîòêàçíîé ðàáîòû) íà åäèíèöó ñòîèìîñòè (èëè

äðóãîãî îãðàíè÷èâàþùåãî ïàðàìåòðà):

d(k

,...,k

+1,...,k

) =

= [P(k

,...,k

+1,...,k

) – P(k

,...,k

)]/c

. (5.87)

...

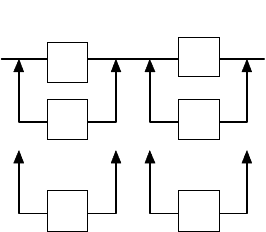
Ðèñ.5.21. Ðåçåðâèðîâàíèå

ìåùåíèåì

193

Ïðèìåð 5.15. Ïðèìåíåíèå

ìåòîäà íàèñêîðåéøåãî ñïóñêà

ðàññìîòðèì íà ïðèìåðå ïîýëå-

ìåíòíîãî ðåçåðâèðîâàíèÿ ñèñ-

òåìû èç äâóõ ïîñëåäîâàòåëüíî

ñîåäèíåííûõ ýëåìåíòîâ ïðè

óñëîâèÿõ, ïðèâåäåííûõ â ïðè-

ìåðå 5.14, íî ñ èñïîëüçîâàíèåì

íåíàãðóæåííîãî ðåçåðâèðîâà-

íèÿ çàìåùåíèåì îòêàçàâøèõ

ýëåìåíòîâ (ðèñ.5.21) [46]. Òà-

êèå èëè àíàëîãè÷íûå çàäà÷è

÷àñòî âîçíèêàþò ïðè êîìïëåê-

òîâàíèè îïòèìàëüíîãî íàáîðà

çàïàñíûõ ýëåìåíòîâ äëÿ òåõíè-

÷åñêîãî îáñëóæèâàíèÿ è ðå-

ìîíòà òåõíè÷åñêèõ îáúåêòîâ

(ñì.ãë.6).

Âåðîÿòíîñòü áåçîòêàçíîé

ðàáîòû òàêîé ñèñòåìû äëÿ

èäåíòè÷íûõ ïî íàäåæíîñòè

ýëåìåíòîâ êàæäîé ãðóïïû

( ) ( ) ( )

Pkk PkPk

k k

12 11 2 2

1 2

! !

= × =-

. (5.88)

Ïðè ðåàëèçàöèè ìåòîäà íàèñêîðåéøåãî ñïóñêà íà êàæäîì øàãå ðàññ÷èòûâàþòñÿ âå-

ðîÿòíîñòè áåçîòêàçíîé ðàáîòû ïðè äîáàâëåíèè îäíîãî ýëåìåíòà ê êàæäîé èç ãðóïï

( ) ( ) ( )

( )

Pk k Pk Pk

k k

1 2 11 2 2

1 1 1

1 2

+ = +× =-

! !

, (5.89)

( ) ( ) ( )

( )

Pkk PkPk

k k

12 11 2 2

1 11

1 2

! !

+= × +=-

(5.90)

è óäåëüíûå ïðèðàùåíèÿ íàäåæíîñòè íà åäèíèöó ñòîèìîñòè

d(k

+1,k

) = [P(k

+1,k

) – P(k

)]/c

, (5.91)

d(k

+1) = [P(k

+1) – P(k

)]/c

. (5.92)

Çàòåì íà êàæäîì øàãå ê ñèñòåìå äîáàâëÿåòñÿ òîò ýëåìåíò, êîòîðûé îáåñïå÷èâàåò

ìàêñèìàëüíîå óäåëüíîå ïðèðàùåíèå íàäåæíîñòè d=max{d(k

+1,k

),d(k

+1)}. Äëÿ íî-

âîé ñèñòåìû ïðîâåðÿåòñÿ âûïîëíåíèå îãðàíè÷åíèé è ðàñ÷åòû ïîâòîðÿþòñÿ íà íîâîì

øàãå. Ðåçóëüòàòû ðàñ÷åòîâ äëÿ óêàçàííûõ óñëîâèé ñâåäåíû â òàáë.5.4.

Ðàñ÷åòû ïîêàçûâàþò, ÷òî îïòèìàëüíàÿ ñèñòåìà ñîñòîèò èç òðåõ ýëåìåíòîâ ïåðâîé è

÷åòûðåõ ýëåìåíòîâ âòîðîé ãðóïïû. Ïðè ýòîì âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû ñèñòåìû

P(k

)=0,9929, åå ñóììàðíàÿ ñòîèìîñòü C(k

)=15 óñë.åä.

Ìîäèôèêàöèåé ìåòîäà íàèñêîðåéøåãî ñïóñêà ÿâëÿåòñÿ ìåòîä ìàêñè-

ìàëüíîãî ýëåìåíòà, êîòîðûé èñïîëüçóåòñÿ ïðè ðåøåíèè êîìïëåêñíûõ çà-

äà÷ îïòèìèçàöèè ïîêàçàòåëåé íàäåæíîñòè ñëîæíûõ ñèñòåì [3].

5.5. Надежность систем с восстановлением

Äëÿ íåðåçåðâèðîâàííûõ ñèñòåì âîññòàíîâëåíèå îòêàçàâøèõ ýëåìåíòîâ

íå èçìåíÿåò çíà÷åíèÿ âåðîÿòíîñòè áåçîòêàçíîé ðàáîòû, íî ïðèâîäèò ê ïî-

âûøåíèþ êîìïëåêñíûõ ïîêàçàòåëåé íàäåæíîñòè (íàïðèìåð, êîýôôèöèåíòà

ãîòîâíîñòè). Ïðè ðåçåðâèðîâàíèè âîññòàíîâëåíèå ÿâëÿåòñÿ îäíèì èç äåé-

ñòâåííûõ ìåòîäîâ ïîâûøåíèÿ íàäåæíîñòè â öåëîì, â òîì ÷èñëå è âåðîÿò-

íîñòè áåçîòêàçíîé ðàáîòû.

Äëÿ ðàñ÷åòà íàäåæíîñòè ñèñòåìû ñ âîññòàíîâëåíèåì ìåòîäû, èçëîæåí-

íûå â ðàçä.5.2, ïðàêòè÷åñêè íåïðèìåíèìû. ×àùå âñåãî èñïîëüçóåòñÿ òîïî-

ëîãè÷åñêèé ìåòîä ñ ïîñòðîåíèåì ãðàôà ñîñòîÿíèé [5,12,13].

Òàáëèöà 5.4

ОПТИМИЗАЦИЯ МЕТОДОМ НАИСКОРЕЙШЕГО СПУСКА

Í î ì å ð ø à ã à

Ïàðàìåòðû

1 2 3 4 5

1 2 2 3 3

1 1 2 2 3

)

0,7 0,955

0,955

0,9955

)

0,5 0,5 0,875

0,875

0,9792

P(k

)

0,35 0,4775

0,8356

0,8711

0,9748

+1)

0,955

0,9955

0,9997

P(k

+1,k

)

0,4775

0,4978

0,8711

0,8747

0,9788

+1,k

)

0,1275

0,0203

0,0354

0,0036

0,0041

+1)

0,875

0,9792

0,9974

P(k

+1)

0,6125

0,8356

0,9351

0,9748

0,9929

+1)

0,0875

0,1194

0,0332

0,0346

0,0060

2 2 3 3 3

1 2 2 3 4

194

5.5.1. Граф состояний технической системы

Ãðàô ñîñòîÿíèé òåõíè÷åñêîé ñèñòåìû (ãðàô ïåðåõîäîâ) - îäíà èç

ãðàôè÷åñêèõ ôîðì ìàòåìàòè÷åñêîé ìîäåëè íàäåæíîñòè òåõíè÷åñêîé ñèñ-

òåìû, â êîòîðîé âîçìîæíûå ñîñòîÿíèÿ ñèñòåìû èçîáðàæàþòñÿ â âèäå òî-

÷åê (âåðøèí ãðàôà), à âîçìîæíûå íàïðàâëåíèÿ ïåðåõîäîâ èç îäíîãî ñî-

ñòîÿíèÿ â äðóãîå - â âèäå ñòðåëîê, ñîåäèíÿþùèõ âåðøèíû (ðåáåð ãðàôà).

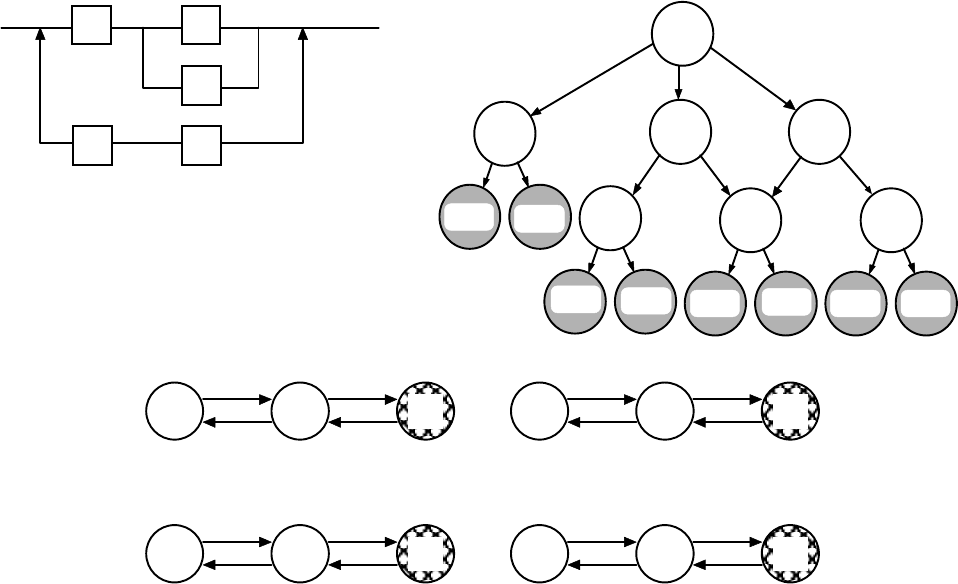
Íà ðèñ.5.22 ïðåäñòàâëåíû òèïîâûå ãðàôû ñîñòîÿíèé íàèáîëåå ÷àñòî âñòðå÷àþùèõñÿ

ñîåäèíåíèé ýëåìåíòîâ: ïîñëåäîâàòåëüíîãî, ïàðàëëåëüíîãî (èëè íàãðóæåííîãî ðåçåðâà)

è íåíàãðóæåííîãî ðåçåðâà. Âåðøèíû ãðàôà îáîçíà÷åíû êîäîì, â êîòîðîì ÷èñëî çíàêîâ

ðàâíî ÷èñëó ýëåìåíòîâ, ìåñòî çíàêà ñîîòâåòñòâóåò íîìåðó ýëåìåíòà, ðàáîòîñïîñîáíîå

ñîñòîÿíèå ýëåìåíòà îáîçíà÷åíî öèôðîé 1, íåðàáîòîñïîñîáíîå (îòêàç) - 0. Îêîëî ðåáåð

ãðàôà óêàçàíû èíòåíñèâíîñòè ïåðåõîäîâ èç ñîñòîÿíèÿ â ñîñòîÿíèå (èíòåíñèâíîñòè îò-

êàçîâ ýëåìåíòîâ). Íåðàáîòîñïîñîáíûå ñîñòîÿíèÿ ñèñòåìû âûäåëåíû øòðèõîâêîé.

Ïðè ïîñòðîåíèè ãðàôà ñîñòîÿíèé íåîáõîäèìî ðóêîâîäñòâîâàòüñÿ ñëå-

äóþùèìè îñíîâíûìè ïðàâèëàìè [5]: ïîñòðîåíèå íà÷èíàåòñÿ ñ ñîñòîÿíèÿ, â

êîòîðîì âñå ýëåìåíòû ñèñòåìû ðàáîòîñïîñîáíû, ýòîé âåðøèíå, êàê ïðàâèëî,

ïðèñâàèâàåòñÿ íîìåð 0; êàæäîå ïîñëåäóþùåå ñîñòîÿíèå ïîëó÷àåòñÿ èç ïðå-

äûäóùåãî ïðè îòêàçå îäíîãî èç ýëåìåíòîâ ñèñòåìû; êîëè÷åñòâî ïîñëåäóþ-

ùèõ ñîñòîÿíèé ðàâíî êîëè÷åñòâó ýëåìåíòîâ, êîòîðûå ìîãóò îòêàçàòü â ïðå-

äûäóùåì ñîñòîÿíèè (ñ÷èòàåòñÿ, ÷òî íåðàáîòàþùèå è íåðàáîòîñïîñîáíûå

ýëåìåíòû îòêàçàòü íå ìîãóò); ñîñòîÿíèÿ, ñîâïàäàþùèå ïî ñî÷åòàíèþ ñî-

ñòîÿíèé ýëåìåíòîâ, îáúåäèíÿþòñÿ â îäíó âåðøèíó ãðàôà; íîâûå ñîñòîÿíèÿ

(âåðøèíû ãðàôà) äîáàâëÿþòñÿ äî òåõ ïîð, ïîêà âñå ñîñòîÿíèÿ íå ñòàíóò íå-

ðàáîòîñïîñîáíûìè; âñå íåðàáîòîñïîñîáíûå ñîñòîÿíèÿ ñèñòåìû ÿâëÿþòñÿ

êîíå÷íûìè âåðøèíàìè ãðàôà (ñ÷èòàåòñÿ, ÷òî íåðàáîòîñïîñîáíàÿ ñèñòåìà

óæå íå ìîæåò îòêàçàòü), òàêèå ñîñòîÿíèÿ è ñîîòâåòñòâóþùèå èì âåðøèíû

ãðàôà äëÿ ñèñòåì áåç âîññòàíîâëåíèÿ íàçûâàþòñÿ ïîãëîùàþùèìè.

Ïðè ïîñòðîåíèè ãðàôà ñîñòîÿíèé öåëåñîîáðàçíî âîñïîëüçîâàòüñÿ ìåòîäîì äåêîìïî-

çèöèè è ïðåäâàðèòåëüíî ïîñòðîèòü ãðàôû ïîäñèñòåì, â òîì ÷èñëå ïîäñèñòåì ñ ðåçåðâè-

ðîâàíèåì. Î÷åâèäíî, ïðè íàãðóæåííîì ðåçåðâèðîâàíèè òàê æå, êàê è ïðè ïàðàëëåëüíîì

ñîåäèíåíèè ýëåìåíòîâ, âñå ïóòè ãðàôà ïîäñèñòåìû ñõîäÿòñÿ ê îäíîìó êîíå÷íîìó ñî-

ñòîÿíèþ, ñîîòâåòñòâóþùåìó îòêàçó âñåõ ýëåìåíòîâ ïîäñèñòåìû (ñì.ðèñ.5.22á), à êî-

íå÷íûå ñîñòîÿíèÿ ãðàôà îñíîâíîé ïîäñèñòåìû ÿâëÿþòñÿ íà÷àëüíûìè ñîñòîÿíèÿìè äëÿ

ïîäñèñòåìû, íàõîäÿùåéñÿ â íåíàãðóæåííîì ðåçåðâå (ñì.ðèñ.5.22â).

Ïðèìåð 5.16. Íà ðèñ.5.23 ïðåäñòàâëåíû ñòðóêòóðíàÿ ñõåìà è ãðàô ñîñòîÿíèé ñèñ-

òåìû, ñîäåðæàùåé ïîñëåäîâàòåëüíîå (ýëåìåíòû 1 è 2) è ïàðàëëåëüíîå (2 è 3) ñîåäèíå-

íèÿ ýëåìåíòîâ, à òàêæå íåíàãðóæåííûé ðåçåðâ (4 è 5) [5].

21 3

110 111 011

101

10 11 01

11 01 00

1 20

à) á) â)

Ðèñ.5.22. Òèïîâûå ãðàôû ñîñòîÿíèé òåõíè÷åñêèõ ñèñòåì:

ïîñëåäîâàòåëüíîãî (à) è ïàðàëëåëüíîãî ñîåäèíåíèé (á), íåíàãðóæåííîãî ð

çåðâà (â)

195

Âîññòàíîâëåíèå îòêàçàâøåãî ýëåìåíòà - ïðîöåññ åãî ïåðåâîäà èç íåðà-

áîòîñïîñîáíîãî ñîñòîÿíèÿ â ðàáîòîñïîñîáíîå. Ïîýòîìó â ãðàôå ñîñòîÿíèé

ñèñòåì ñ âîññòàíîâëåíèåì íàðÿäó ñ ïåðåõîäàìè èç ïðåäûäóùèõ ñîñòîÿíèé

â ïîñëåäóþùèå äîëæíû áûòü óêàçàíû è îáðàòíûå ïåðåõîäû èç ïîñëåäóþ-

ùèõ ñîñòîÿíèé â ïðåäûäóùèå ñ èíòåíñèâíîñòÿìè âîññòàíîâëåíèÿ m

Ïðèìåð 5.17. Íà ðèñ.5.24 ïðåäñòàâëåíû ãðàôû ñîñòîÿíèé ÷åòûðåõ âàðèàíòîâ äóá-

ëèðîâàíèÿ ýëåìåíòà ñ âîññòàíîâëåíèåì: íàãðóæåííîãî ðåçåðâà ñ âîññòàíîâëåíèåì ýëå-

ìåíòîâ ïî îäíîìó èëè äâóõ îäíîâðåìåííî (âîññòàíîâëåíèå áåç îãðàíè÷åíèé), íàãðó-

æåííîãî ðåçåðâà ñ âîññòàíîâëåíèåì ýëåìåíòîâ òîëüêî ïî îäíîìó (îãðàíè÷åííîå âîññòà-

íîâëåíèå), íåíàãðóæåííîãî ðåçåðâà ñ âîññòàíîâëåíèåì áåç îãðàíè÷åíèé è íåíàãðóæåí-

íîãî ðåçåðâà ñ îãðàíè÷åííûì âîññòàíîâëåíèåì [5]. Öèôðàìè îáîçíà÷åíû ñîñòîÿíèÿ

(âåðøèíû ãðàôà): 0 - îáà ýëåìåíòà ðàáîòîñïîñîáíû, 1 - îòêàçàë îäèí èç ýëåìåíòîâ (îñ-

íîâíîé èëè ðåçåðâíûé), 3 - îòêàçàëè îáà ýëåìåíòà. Ïðè ýòîì ýëåìåíòû ñ÷èòàþòñÿ

èäåíòè÷íûìè ïî íàäåæíîñòè è âîññòàíîâëåíèþ, ò.å. l

=l, m

=m.

5.5.2. Расчет надежности систем с восстановлением

Ïðè ðàñ÷åòå íàäåæíîñòè ñèñòåì ñ âîññòàíîâëåíèåì ñ èñïîëüçîâàíèåì

ãðàôîâ ñîñòîÿíèé íåîáõîäèìî ó÷èòûâàòü íåêîòîðûå îñîáåííîñòè ñèñòåìû.

Â çàâèñèìîñòè îò íàçíà÷åíèÿ è ðåæèìà ïðèìåíåíèÿ ñèñòåìû ê íåé ìîãóò

ïðåäúÿâëÿòüñÿ ðàçëè÷íûå òðåáîâàíèÿ. Íàïðèìåð, åñëè ïîñëå âêëþ÷åíèÿ

ñèñòåìà äîëæíà áåçîòêàçíî ðàáîòàòü çàäàííîå âðåìÿ è ïåðåðûâû â ðàáîòå

íåäîïóñòèìû, òî äëÿ òàêèõ ñèñòåì ðàññ÷èòûâàåòñÿ âåðîÿòíîñòü íåïðåðûâ-

íîé áåçîòêàçíîé ðàáîòû (óñëîâíàÿ âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû). Ïðè

ýòîì âîçìîæíîñòü îáðàòíûõ ïåðåõîäîâ èç íåðàáîòîñïîñîáíûõ (ïîãëîùàþ-

11111

01111

10111

11011

01101

01110

00111

00101

00110

10011

10001 10010

01011

01001

01010

à)

á)

Ðèñ.5.23. Ñòðóêòóðíàÿ ñõåìà (à)

è ãðàô ñîñòîÿíèé (á)

1 2

à)

0 1 2

2l l

m 2m

á)

0 1 2

2l l

m m

â)

0 1 2

l l

m 2m

ã)

0 1 2

l l

m m

Ðèñ.5.24. Ãðàôû ñîñòîÿíèé ñèñòåì äóáëèðîâàíèÿ ñ âîññòàíîâëåíèåì: íàãðóæåííûé (à,á)

è íåíàãðóæåííûé (â,ã) ðåçåðâ ñ îãðàíè÷åííûì (á,ã) è íåîãðàíè÷åííûì (à,â) âîññòàíîâ-

ëåíèåì

196

ùèõ) ñîñòîÿíèé â ðàáîòîñïîñîáíûå

íå ðàññìàòðèâàåòñÿ. Åñëè æå ïåðå-

ðûâû â ðàáîòå ñèñòåìû äëÿ âîññòà-

íîâëåíèÿ ýëåìåíòîâ äîïóñêàþòñÿ,

íî âåðîÿòíîñòü çàñòàòü ñèñòåìó â

ðàáîòîñïîñîáíîì ñîñòîÿíèè â çà-

äàííûé ìîìåíò âðåìåíè äîëæíà

áûòü äîñòàòî÷íî âûñîêîé (ò.å.

áîëüøîå çíà÷åíèå èìååò ãîòîâíîñòü

ñèñòåìû ê ôóíêöèîíèðîâàíèþ), òî

äëÿ òàêèõ ñèñòåì îïðåäåëÿþòñÿ êî-

ýôôèöèåíòû ãîòîâíîñòè èëè êîýô-

ôèöèåíò îïåðàòèâíîé ãîòîâíîñòè.

Ïðè ýòîì äîïóñêàåòñÿ âîçìîæíîñòü

îáðàòíûõ ïåðåõîäîâ èç íåðàáîòî-

ñïîñîáíûõ (â äàííîì ñëó÷àå îò-

ðàæàþùèõ) ñîñòîÿíèé â ðàáîòî-

ñïîñîáíûå.

Ïóñòü äëÿ ñèñòåìû èçâåñòíû âåðîÿòíîñòè âñåõ ñîñòîÿíèé â ìîìåíò

âðåìåíè t. Ðàññìîòðèì èçìåíåíèå ñîñòîÿíèÿ ñèñòåìû ÷åðåç ìàëûé ïðîìå-

æóòîê âðåìåíè Dt, íàñòîëüêî ìàëûé, ÷òî âåðîÿòíîñòü òîãî, ÷òî â òå÷åíèå

ýòîãî âðåìåíè ïðîèçîéäåò áîëåå îäíîãî ñîáûòèÿ (îòêàçà èëè âîññòàíîâëå-

íèÿ ýëåìåíòà) ïðåíåáðåæèìî ìàëà. Â ìîìåíò âðåìåíè t+Dt ñèñòåìà ìîæåò

íàõîäèòüñÿ â k-îì ñîñòîÿíèè (ðèñ.5.25) òîëüêî â îäíîì èç ñëåäóþùèõ ñëó-

÷àåâ:

1) Â ìîìåíò t ñèñòåìà íàõîäèëàñü â îäíîì èç ïðåäûäóùèõ ñîñòîÿíèé i

(i=1,2,...,n), è â òå÷åíèå âðåìåíè Dt îòêàçàë îäèí èç ýëåìåíòîâ, ò.å. ïðî-

èçîøåë îäèí èç ïåðåõîäîâ i®k. Åñëè íàäåæíîñòü ýëåìåíòîâ ïîä÷èíÿåòñÿ

ýêñïîíåíöèàëüíîìó çàêîíó, òî âåðîÿòíîñòü êàæäîãî òàêîãî ïåðåõîäà

(t,t+Dt) = q

(Dt) = 1 – exp(–l

Dt) » l

Dt, (5.93)

ãäå q

è l

- âåðîÿòíîñòü è èíòåíñèâíîñòü îòêàçîâ ýëåìåíòà, ðàáîòîñïîñîáíîñòü êîòîðî-

ãî îïðåäåëÿåò ïðÿìîé ïåðåõîä èç i-ãî ñîñòîÿíèÿ â k-îå.

2) Â ìîìåíò t ñèñòåìà íàõîäèëàñü â îäíîì èç ïîñëåäóþùèõ ñîñòîÿíèé j

(j=1,2,...,m), è â òå÷åíèå âðåìåíè Dt áûë âîññòàíîâëåí îäèí ýëåìåíò, ò.å.

ïðîèçîøåë îäèí èç îáðàòíûõ ïåðåõîäîâ j®k. Åñëè ïðîöåññ âîññòàíîâëåíèÿ

ïîä÷èíÿåòñÿ ýêñïîíåíöèàëüíîìó çàêîíó, òî âåðîÿòíîñòü òàêîãî ïåðåõîäà

(t,t+Dt) = p

âj

(Dt) = 1 – exp(–m

Dt) » 1 – (1 – m

Dt) = m

Dt, (5.94)

ãäå p

âj

è m

- âåðîÿòíîñòü è èíòåíñèâíîñòü âîññòàíîâëåíèÿ ýëåìåíòà, ðàáîòîñïîñîá-

íîñòü êîòîðîãî îïðåäåëÿåò îáðàòíûé ïåðåõîä èç j-ãî ñîñòîÿíèÿ â k-îå.

3) â ìîìåíò âðåìåíè t ñèñòåìà óæå íàõîäèëàñü â k-îì ñîñòîÿíèè, è â

òå÷åíèå âðåìåíè Dt íè îäèí èç ðàáîòîñïîñîáíûõ ýëåìåíòîâ íå îòêàçàë è

íè îäèí èç îòêàçàâøèõ íå áûë âîññòàíîâëåí, ò.å. íå ñîñòîÿëèñü íè ïðÿìûå

(k®j, i=1,2,...,m), íè îáðàòíûå (k®j, i=1,2,...,n) ïåðåõîäû. Âåðîÿòíîñòè

ýòèõ ñîáûòèé, ñîîòâåòñòâåííî:

( ) ( ) ( )

(

)

[

]

ptt t ptt t q t t t

kj kj j kj kj

, , exp+ =- + =- =- - - »-D D D D D1 1 11 1l l , (5.95)

Текущее

состояние

Предыдущие

состояния

Последующие

состояния

Ðèñ.5.25. Ôðàãìåíò ãðàôà ñîñòîÿíèé

ñèñòåìû ñ âîññòàíîâë

íèåì

197

(

)

(

)

(

)

(

)

[

]

ptt t ptt t p t t t

ki ki âi ki ki

, , exp+ =- + =- =- - - »-D D D D D1 1 11 1m m , (5.96)

ãäå q

è l

- âåðîÿòíîñòü è èíòåíñèâíîñòü îòêàçîâ ýëåìåíòà, ðàáîòîñïîñîáíîñòü êîòîðî-

ãî îïðåäåëÿåò ïðÿìîé ïåðåõîä k®j, p

âi

è m

- âåðîÿòíîñòü è èíòåíñèâíîñòü âîññòàíîâ-

ëåíèé ýëåìåíòà, ðàáîòîñïîñîáíîñòü êîòîðîãî îïðåäåëÿåò îáðàòíûé ïåðåõîä k®i.

×òîáû â ìîìåíò t+Dt ñèñòåìà îêàçàëàñü â k-îì ñîñòîÿíèè, íåîáõîäèìî,

÷òîáû ëèáî ñîñòîÿëñÿ ïåðåõîä ïåðâîãî èëè âòîðîãî âèäà, ëèáî íå ñîñòîÿë-

ñÿ íè îäèí èç ïåðåõîäîâ òðåòüåãî âèäà. Ïî òåîðåìå ñëîæåíèÿ âåðîÿòíî-

ñòåé (äëÿ ïåðâîãî è âòîðîãî ñëó÷àÿ) è ïî òåîðåìå óìíîæåíèÿ âåðîÿòíî-

ñòåé (äëÿ òðåòüåãî) âåðîÿòíîñòü k-ãî ñîñòîÿíèÿ ñèñòåìû â ìîìåíò âðåìåíè

t+Dt

(

)

() ( ) () ( ) () ( ) ( )

() () ()

( )

() () ()

Pt t

Ptptt t Ptptt tPt ptt t ptt t

Pt t Pt tPt t t

t Pt t Pt Pt t

i ik j jk

k kj

i ik

j jk

k kj

iki

jkj

k kj

+ =

= + + + + + +

» + + - -

» + + -

= =

= = =

å Õ Õå

å å Õ Õ

å å

D D D D

D D D

, , , ,

1 1

1 1 1

1 1

l m l m

l m l

å å

D m

() () ()

» + + - -

= = = =

å å å å

D D D Dt Pt t Pt Pt t t

iki

jkj

k kj

l m l m

1 1 1 1

1 , (5.97)

ãäå P

(t), P

(t) è P

(t) - âåðîÿòíîñòè ïðåäûäóùèõ, ïîñëåäóþùèõ ñîñòîÿíèé è k-ãî ñî-

ñòîÿíèÿ â ìîìåíò âðåìåíè t.

Èç âûðàæåíèÿ (5.97) ìîæíî ïîëó÷èòü

( ) ()

() () ()

Pt t Pt

Pt Pt Pt

k k

iki

jkj

k kj

+ -

= + - +

= = = =

å å å å

l m l m

1 1 1 1

. . (5.98)

Ïåðåõîäÿ ê ïðåäåëó ïðè Dt®0, ïîëó÷èì äèôôåðåíöèàëüíîå óðàâíåíèå îò-

íîñèòåëüíî íåèçâåñòíîé ôóíêöèè P

(t)

()

() () ()

dPt

Pt Pt Pt

iki

jkj

k kj

= + - +

= = = =

å å å å

l m l m

1 1 1 1

. (5.99)

Ñîñòàâèâ äëÿ êàæäîãî èç N+1 ñîñòîÿíèé óðàâíåíèå âèäà (5.99), ïîëó-

÷èì ñèñòåìó N+1 äèôôåðåíöèàëüíûõ óðàâíåíèé. Òàê êàê ñèñòåìà ëèíåéíî

çàâèñèìà (ñóììà ïðàâûõ ÷àñòåé óðàâíåíèé ðàâíà íóëþ), òî äëÿ åå ðåøå-

íèÿ îäíî ëþáîå óðàâíåíèå íåîáõîäèìî çàìåíèòü íîðìèðóþùèì óñëîâèåì

()

1. (5.100)

Â êà÷åñòâå íà÷àëüíûõ óñëîâèé ìîæíî âîñïîëüçîâàòüñÿ çíà÷åíèÿìè

(0) = 1, P

(0) = P

(0) = ... = P

(0) = 0, (5.101)

Ïðè ðåøåíèè ñèñòåìû óðàâíåíèé ìîæíî âîñïîëüçîâàòüñÿ ïðåîáðàçîâà-

íèåì Ëàïëàñà äëÿ èçîáðàæåíèÿ ïðîèçâîäíîé P¢(t) [26]

198

()

[ ]

()

[ ]

() () ( ) ()

LPt zLPt P zPt ztdt P

= - = - -

0 0

exp , (5.102)

Òîãäà óðàâíåíèå âèäà (5.99) ïðèìåò âèä

()

[ ]

() ()

[ ]

()

[ ]

()

[ ]

zLPt P LPt LPt LPt

k k ik i

jk j

k kj

- = + - +

= = = =

å å å å

1 1 1 1

l m l m (5.103)

è ñèñòåìà äèôôåðåíöèàëüíûõ óðàâíåíèé ñâîäèòñÿ ê ñèñòåìå ëèíåéíûõ àë-

ãåáðàè÷åñêèõ óðàâíåíèé îòíîñèòåëüíî íåèçâåñòíûõ L[P

(t)]

()

[ ]

()

[ ]

()

[ ]

()

z LPt LPt LPt P

k ik i

jk j

+ +

- - =

= = = =

å å å å

l m l m

1 1 1 1

0 (5.104)

ñ íîðìèðóþùèì óñëîâèåì (5.100) â âèäå

()

[ ]

zLPt

1. (5.105)

Ðåøèâ ñèñòåìó îòíîñèòåëüíî L[P

(t)] è ïðèìåíèâ çàòåì îáðàòíîå ïðå-

îáðàçîâàíèå Ëàïëàñà [26], ìîæíî íàéòè âåðîÿòíîñòè ñîñòîÿíèé P

(t).

Íåñòàöèîíàðíûé êîýôôèöèåíò ãîòîâíîñòè K(t) (ôóíêöèÿ ãîòîâíîñòè -

âåðîÿòíîñòü ðàáîòîñïîñîáíîñòè ñèñòåìû â ìîìåíò âðåìåíè t) ðàññ÷èòûâà-

åòñÿ êàê ñóììà âåðîÿòíîñòåé âñåõ åå ðàáîòîñïîñîáíûõ ñîñòîÿíèé

() ()

Kt Pt

(5.106)

ãäå P

(t) - âåðîÿòíîñòü íà÷àëüíîãî ñîñòîÿíèÿ (ïðè âñåõ ðàáîòîñïîñîáíûõ ýëåìåíòàõ),

(t) - âåðîÿòíîñòü k-ãî ñîñòîÿíèÿ, N

- ÷èñëî ðàáîòîñïîñîáíûõ ñîñòîÿíèé.

Ïðè îïðåäåëåíèè êîýôôèöèåíòà ãîòîâíîñòè ñèñòåìû (ñì.ðàçä.1.4)

()

T T

®¥

lim (5.107)

ðàññìàòðèâàåòñÿ óñòàíîâèâøèéñÿ ðåæèì ýêñïëóàòàöèè (t®¥), ïðè êîòî-

ðîì ïðîèçâîäíûå âåðîÿòíîñòåé âñåõ ñîñòîÿíèé ñèñòåìû P¢(t)=0. Ïðè ýòîì

ñèñòåìà äèôôåðåíöèàëüíûõ óðàâíåíèé (5.99) ñðàçó ïðåâðàùàåòñÿ â ñèñòå-

ìó ëèíåéíûõ àëãåáðàè÷åñêèõ óðàâíåíèé âèäà

() () ()

l m l m

iki

jkj

k kj

Pt Pt Pt

= = = =

å å å å

+ - +

1 1 1 1

0. (5.108)

Äëÿ îïðåäåëåíèÿ óñëîâíîé âåðîÿòíîñòè áåçîòêàçíîé ðàáîòû èç ãðàôà

ñîñòîÿíèé è ñèñòåìû óðàâíåíèé (5.99) èñêëþ÷àþòñÿ îáðàòíûå ïåðåõîäû èç

ïîãëîùàþùèõ ñîñòîÿíèé (èç âñåõ êîíå÷íûõ âåðøèí ãðàôà).

Ïðèìåð 5.18. Äëÿ íàãðóæåííîãî äóáëèðîâàíèÿ ñ âîññòàíîâëåíèåì áåç îãðàíè÷åíèé

(ðèñ.5.24à) ïîëíàÿ ñèñòåìà óðàâíåíèé (5.99) èìååò âèä [5]:

(

)

(

)

(

)

() () ( ) () ()

() () ()

=- +

= - + +

= -

Pt Pt Pt

Pt Pt Pt Pt

Pt Pt Pt

0 0 1

1 0 1 2

2 1 2

2 2

l m

l l m m

l m

(5.109)

Äëÿ íàãðóæåííîãî äóáëèðîâàíèÿ ñ îãðàíè÷åííûì âîññòàíîâëåíèåì (ðèñ.5.24á):

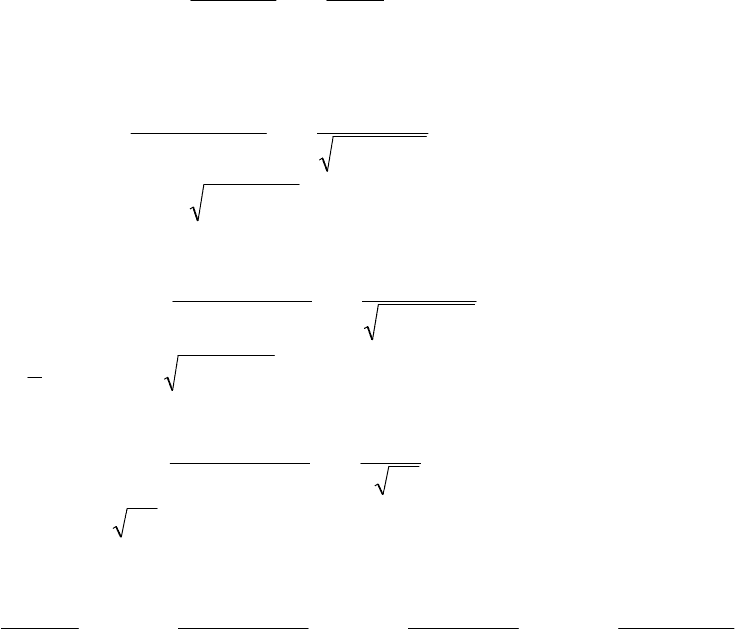
199

(

)

(

)

(

)

() () ( ) () ()

() () ()

=- +

= - + +

= -

Pt Pt Pt

Pt Pt Pt Pt

Pt Pt Pt

0 0 1

1 0 1 2

2 1 2

l m

l l m m

l m

(5.110)

Äëÿ íåíàãðóæåííîãî äóáëèðîâàíèÿ ñ âîññòàíîâëåíèåì áåç îãðàíè÷åíèé (ðèñ.5.24â)

(

)

(

)

(

)

() () ( ) () ()

() () ()

=- +

= - + +

= -

Pt Pt Pt

Pt Pt Pt Pt

Pt Pt Pt

0 0 1

1 0 1 2

2 1 2

l m

l l m m

l m

(5.111)

Äëÿ íåíàãðóæåííîãî äóáëèðîâàíèÿ ñ îãðàíè÷åííûì âîññòàíîâëåíèåì (ðèñ.5.24ã)

(

)

(

)

(

)

() () ( ) () ()

() () ()

=- +

= - + +

= -

Pt Pt Pt

Pt Pt Pt Pt

Pt Pt Pt

0 0 1

1 0 1 2

2 1 2

l m

l l m m

l m

(5.112)

Ñèñòåìû óðàâíåíèé (5.109)-(5.112) äîïîëíÿþòñÿ íîðìèðóþùèì óñëîâèåì (5.100):

() () () ()

Pt Pt Pt Pt

= + + =

0 1

. (5.113)

Íåñòàöèîíàðíûé êîýôôèöèåíò ãîòîâíîñòè

() () () () ()

Kt Pt Pt Pt Pt

= = + = -

0 1 2

. (5.114)

Äëÿ íàãðóæåííîãî äóáëèðîâàíèÿ ñ âîññòàíîâëåíèåì áåç îãðàíè÷åíèé (ðèñ.5.24à)

()

( )

( ) ( )

[ ]

Kt t t= -

1 1

1 2 2 1

l m

a a a aexp exp

, (5.115)

ãäå a

= –2(l+m), a

= –(l+m).

Äëÿ íàãðóæåííîãî äóáëèðîâàíèÿ ñ îãðàíè÷åííûì âîññòàíîâëåíèåì (ðèñ.5.24á)

()

( )

( ) ( )

[ ]

Kt t t= -

+ +

1 2 2 1

l m l

l lm

b b b bexp exp

, (5.116)

ãäå

b l m l lm

05 3 2 4

,=- × + ± +

Äëÿ íåíàãðóæåííîãî äóáëèðîâàíèÿ ñ âîññòàíîâëåíèåì áåç îãðàíè÷åíèé (ðèñ.5.24â)

()

( )

( ) ( )

[ ]

Kt t t= -

+ +

1 1

1 2 2 1

l m m

m lm

g g g gexp exp

, (5.117)

ãäå

g l m m lm

2 3 4

=- + ± +

Äëÿ íåíàãðóæåííîãî äóáëèðîâàíèÿ ñ îãðàíè÷åííûì âîññòàíîâëåíèåì (ðèñ.5.24ã)

()

( )

( ) ( )

[ ]

Kt t t= -

+ -

1 1

1 2 2 1

l m lm

d d d dexp exp

, (5.118)

ãäå

(

)

d l m lm

12,

=- + ±

Èç ôîðìóë (5.114)-(5.118) ñ ó÷åòîì (5.107) ìîæíî ïîëó÷èòü âûðàæåíèÿ äëÿ ðàñ÷å-

òà êîýôôèöèåíòà ãîòîâíîñòè K

. Äëÿ ðàññìîòðåííûõ âûøå ïðèìåðîâ, ñîîòâåòñòâåííî,

( ) ( )

(

)

( ) ( )

K K K K

ã ã ã ã

+ +

+ -

1 1

2 2

r r

, , ,

, (5.119)

ãäå r = l/m.

Ïðè l = 0,01 ÷

–1

è m = 0,1 ÷

–1

r = 0,1 è, ñîîòâåòñòâåííî, K

= 0,9917; 0,9836;

0,9955; 0,9910. Äëÿ íåðåçåðâèðîâàííîãî ýëåìåíòà ñ âîññòàíîâëåíèåì K

= 0,9091.

Äëÿ îïðåäåëåíèÿ óñëîâíîé âåðîÿòíîñòè áåçîòêàçíîé ðàáîòû íåîáõîäèìî èñêëþ÷èòü

îáðàòíûå ïåðåõîäû èç êîíå÷íîãî ñîñòîÿíèÿ 2 (ïåðåõîäû 2®1 íà ðèñ.5.24). Âåðîÿòíîñòü

áåçîòêàçíîé ðàáîòû íå çàâèñèò îò îãðàíè÷åíèé âîññòàíîâëåíèÿ è äëÿ íàãðóæåííîãî

äóáëèðîâàíèÿ (ðèñ.5.24à è 5.28á) ñèñòåìó óðàâíåíèé ìîæíî çàïèñàòü â âèäå:

200

(

)

(

)

(

)

() () ( ) ()

() ()

=- +

= - +

Pt Pt Pt

Pt Pt

0 0 1

1 0 1

2 1

l m

l l m

(5.120)

Äëÿ íåíàãðóæåííîãî äóáëèðîâàíèÿ (ðèñ.5.24â è 5.24ã):

(

)

(

)

(

)

() () ( ) ()

() ()

=- +

= - +

Pt Pt Pt

Pt Pt

0 0 1

1 0 1

2 1

l m

l l m

(5.121)

Ðåøåíèå ñèñòåì (5.120) è (5.121) ñ íîðìèðóþùèì óñëîâèåì (5.113) ïðè íà÷àëüíûõ

óñëîâèÿõ (5.101) îòíîñèòåëüíî âåðîÿòíîñòåé ñîñòîÿíèé P

(t), P

(t) è P

(t) äàåò âûðà-

æåíèå äëÿ âåðîÿòíîñòè áåçîòêàçíîé ðàáîòû P(t) = P

(t) + P

(t) = 1 – P

(t) â îáùåì

âèäå:

()

( ) ( )

[ ]

Pt t t=

1 2

1 2 2 1

h h

h h h hexp exp ,

(5.122)

ãäå äëÿ íàãðóæåííîãî äóáëèðîâàíèÿ

h l m l lm m

2 2

3 6

=- + ± + +

, (5.123)

äëÿ íåíàãðóæåííîãî äóáëèðîâàíèÿ

h l m lm m

2 4

.=- + ± +

(5.124)

Äëÿ ðåøåíèÿ ñèñòåì ëèíåéíûõ àëãåáðàè÷åñêèõ óðàâíåíèé (5.104) è (5.108) è íîð-

ìèðóþùèõ óñëîâèé (5.100) è (5.105) ìîæíî òàêæå âîñïîëüçîâàòüñÿ ïðàâèëîì Êðàìåðà,

ïðåäâàðèòåëüíî çàïèñàâ ñèñòåìû óðàâíåíèé â âèäå

(

)

(

)

(

)

() () ()

a z a z a z c

N N NNN N

000 011 0 0

100 111 1 1

00 11

j j j

+ + + =

... ,

...,

... ,

(5.125)

ãäå j

(z)=L[P

(t)] - ïðåîáðàçîâàíèå Ëàïëàñà äëÿ âåðîÿòíîñòè k-ãî ñîñòîÿíèÿ, a

- êîýô-

ôèöèåíò â i-îì óðàâíåíèè (i=0,1,...,N) ïðè k-îì ÷ëåíå, c

(0) - ñâîáîäíûé ÷ëåí i-ãî

óðàâíåíèÿ, N - ÷èñëî âîçìîæíûõ ñîñòîÿíèé ñèñòåìû (áåç íà÷àëüíîãî).

Äëÿ ñèñòåìû óðàâíåíèé (5.125) ïî ïðàâèëó Êðàìåðà:

= D

(z)/D(z), (5.126)

ãäå D(z) - îïðåäåëèòåëü ñèñòåìû àëãåáðàè÷åñêèõ óðàâíåíèé (5.125), D

(z) - îïðåäåëè-

òåëü, â êîòîðîì k-ûé ñòîëáåö êîýôôèöèåíòîâ çàìåíåí ñòîëáöîì ñâîáîäíûõ ÷ëåíîâ:

()

a a a a

k N

N N Nk NN

00 01 0 0

10 11 1 1

0 1

... ...

..................

... ...

()

a a c a

N N N NN

00 01 0 0

10 11 1 1

0 1

... ...

..................

... ...

. (5.127)

Ïî ôîðìóëå (5.106) ïðåîáðàçîâàíèå Ëàïëàñà äëÿ êîýôôèöèåíòà ãîòîâíîñòè

() ()

[ ]

() ()

[ ]

()

j jz LKt L Pt LPt z

k k

= =

= = =

= = ==

å å åå

0 0 00

1 1 11

. (5.128)

Ïðèìåíèâ ê ôóíêöèè (5.128) îáðàòíîå ïðåîáðàçîâàíèå Ëàïëàñà, ìîæíî ïîëó÷èòü

âûðàæåíèå äëÿ êîýôôèöèåíòà ãîòîâíîñòè.

Íà îñíîâàíèè ñèñòåìû óðàâíåíèé (5.99) èëè (5.104) ìîæíî òàêæå îï-

ðåäåëèòü ñðåäíþþ íàðàáîòêó äî îòêàçà. Åñëè èçâåñòíî âûðàæåíèå (5.128)

j(z) = L[K(t)], òî ñðåäíÿÿ íàðàáîòêà äî îòêàçà

( ) () ( ) () ()

[ ]

()

T MT Ktdt ztKtdt LKt

exp= = = -

= =

¥ ¥

ò ò

0 0

0j . (5.129)

Ñëåäîâàòåëüíî, ÷òîáû íàéòè ñðåäíþþ íàðàáîòêó, äîñòàòî÷íî ðåøèòü ñèñ-

òåìó óðàâíåíèé (5.104) ïðè z = 0