Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

382 6. Theory and Application of Mixed Polynomial Matrices













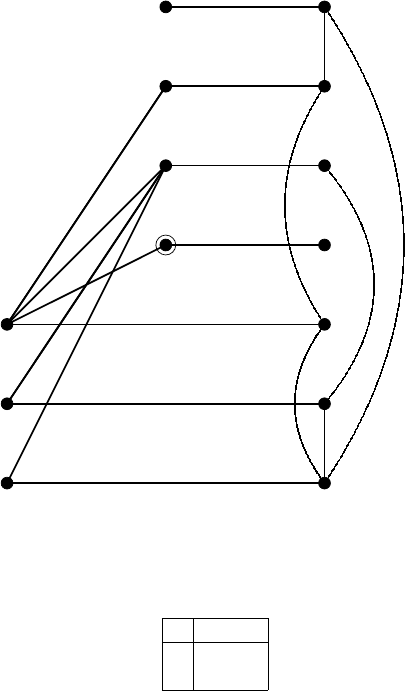
Fig. 6.8. Auxiliary network N in Example 6.4.23

P =

−1 100

1 −100

−1 010

The auxiliary network N =(G, γ)=(V,E, γ) is depicted in Fig. 6.8, where

= ϕ

), x

= ϕ

), etc. The exit is S

−

= {u

}, to which the vertices

not in V

◦

= {x

} are reachable. The subnetwork on G

◦

shown in Fig. 6.9 with the length γ in parentheses, contains directed cycles.

The sum of the lengths along the cycle consisting of {w

}

vanishes, whereas that of {w

} does not. Thus it is revealed, by

Theorem 6.4.18, that this system has a nonzero uncontrollable mode. The

graph-theoretic methods such as Theorem 6.4.7, treating the nonvanishing

entries of F , A,andB of (6.80) as if they were independent, would fail to

detect this fact.

The associated LM-polynomial matrix in (6.73) and its CCF are given

respectively by

6.4 Controllability of Dynamical Systems 383

11000

1 −s −s 10

1 −1 −10 0

−t

0 p

−sp

−t

00−sp

−t

00 p

010−1 1

0011 −1

−t

0 p

−sp

1 −s 1

−t

0 −sp

0 −t

The CCF has the horizontal tail with

= {u, w

} and one square

block with

= {w

}, while the vertical tail is empty. The de-

terminant of the 3 × 3 diagonal block corresponding to

is equal to

−(t

+ t

)s + t

, which has the root s =1/(p

+ p

) when t

=1.

This represents the uncontrollable mode. Thus the CCF reveals directly how

the nonzero uncontrollable mode arises. Finally it is mentioned that the CCF

above is obtained through a unimodular transformation by

U =

⎡

⎣

10 1

00−1

01−s

⎤

⎦









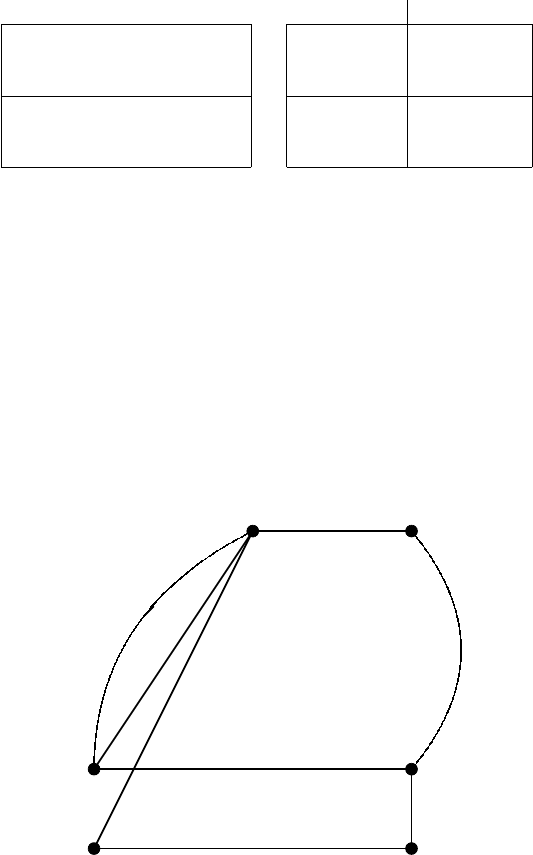
(γ =1)

(0)

(1)

(−1)

(0)

(γ = −1)

(0)

(γ =0)

Fig. 6.9. Subnetwork on G

◦

in Example 6.4.23

Notes. The mixed matrix formulation in §6.4.3 and the algorithm in §6.4.4

are taken from Murota [203].

384 6. Theory and Application of Mixed Polynomial Matrices

6.5 Fixed Modes of Decentralized Systems

Structurally ﬁxed modes of a decentralized control system are investigated

using mixed polynomial matrices. A necessary and suﬃcient condition for the

existence of structurally ﬁxed modes is given along with an eﬃcient algorithm

for testing it.

6.5.1 Fixed Modes

The concept of (decentralized) ﬁxed modes, introduced by Wang–Davison

[332], is recognized as one of the fundamental concepts for the decentralized

control (see

Siljak [300, §1.6], Trave–Titli–Tarras [320]). To be speciﬁc, con-

sider a linear time-invariant dynamical system with ν local control stations

described by

x(t)=Ax(t)+Bu(t), y(t)=Cx(t), (6.81)

where A, B,andC are real matrices, x ∈ R

is the state-vector, u =

, ···, u

)

∈ R

and y =(y

, ···, y

)

∈ R

are the input-vector

and the output-vector, respectively, consisting of the input-vectors u

(k =

1, ···,ν) and the output-vectors y

(k =1, ···,ν) of the local control stations.

The matrices B and C are partitioned into ν blocks as

B =

|···|B

,C=

⎛

⎝

⎞

⎠

in correspondence to the local stations.

The local output feedback is speciﬁed by a block-diagonal matrix

K = diag [K

, ···,K

], (6.82)

which represents the nondynamic decentralized output feedback

u(t)=Ky(t), i.e., u

= K

(k =1, ···,ν).

The local output feedback control with dynamic compensation is described

z(t)=Lz(t)+My(t), u(t)=Nz(t)+Ky(t)+P v(t), (6.83)

where z =(z

, ···, z

)

and v =(v

, ···, v

)

are the state-vector

and the external input-vector, respectively, consisting of the kth feedback

controller (k =1, ···,ν); the matrices L, M, N ,andP are block-diagonal

matrices of appropriate sizes.

Let K be the family of all matrices K of the form (6.82). The greatest

common divisor of the characteristic polynomials of A+BKC, for all K ∈K,

6.5 Fixed Modes of Decentralized Systems 385

is called the ﬁxed polynomial of (A, B, C) with respect to K, and denoted by

ψ(s)=ψ(s; A, B, C, K). Namely,

ψ(s; A, B, C, K)=gcd{det(A + BKC − sI

) | K ∈K}. (6.84)

A complex number λ ∈ C is called a ﬁxed mode of (A, B, C) with respect

to K if λ is an eigenvalue of A + BKC for all K ∈K, or equivalently, if

ψ(λ; A, B, C, K)=0.

The importance of the concept of ﬁxed modes is demonstrated by the

following facts due to Wang–Davison [332] and Corfmat–Morse [41]:

1. The system (6.81) is stabilizable by the decentralized dynamic output

feedback (6.83) if and only if all the ﬁxed modes of (A, B, C) have nega-

tive real parts, and

2. The spectrum of the closed-loop system (6.81) and (6.83) is freely

assignable by means of K ∈Kif and only if there exist no ﬁxed modes

of (A, B, C).

The ﬁxed polynomial and ﬁxed modes can be deﬁned by (6.84) with re-

spect to an arbitrarily speciﬁed family (feedback structure) K of the matrices

K, not necessarily of the form (6.82). A natural choice is to let K be a fam-

ily of matrices K which are subject to an arbitrarily speciﬁed zero/nonzero

structure (cf. Wang–Davison [332], Pichai–Sezer–

Siljak [269]). Namely, for an

m × l matrix

K =(

) with

∈{0, 1} we deﬁne

K = {K | K

=0if

=0}. (6.85)

We refer to the following fundamental result of Anderson–Clements [5]

in a form extended to a general feedback structure and with a proof based

on a rank identity for mixed matrices. We use the notation X =Row(A) 

Col(A)  Row(B)  Col(C), U = Col(B), and Y =Row(C), where |X| = n,

|U| = m,and|Y | = l; and also

= {(I,J) | I ⊆ U, J ⊆ Y,

K[U \ I,Y \ J]=O}. (6.86)

Note that (I,J) ∈C

is a cover of K ∈Kas deﬁned in §2.2.3.

Theorem 6.5.1. Let K and C

be deﬁned by (6.85) and (6.86). For a com-

plex number λ ∈ C and a nonnegative integer d ∈ Z, we have

max

K∈K

rank (A + BKC − λI

) ≤ n − d

if and only if there exists (I,J) ∈C

such that

rank



A − λI

B[X, I]

C[J, X] O



≤ n − d. (6.87)

In particular, λ ∈ C is a ﬁxed mode of (A, B, C) with respect to K if and only

if (6.87) with d =1holds for some (I,J) ∈C

It is understood that (I,J) ∈C

if I = U or J = Y .

386 6. Theory and Application of Mixed Polynomial Matrices

Proof. First note that rank (A + BKC − λI

)=rankD − (m + l)for

D =

⎛

⎝

XUY

XA− λI

UO−I

YCO−I

⎞

⎠

. (6.88)

The maximum of rank D over all K ∈Kis attained when K

= 0 for all

(i, j) with

= 0, and the nonzero entries of K are indeterminates. In this

case, D is a mixed matrix D = Q + T with

Q =

⎛

⎝

A − λI

O −I

CO−I

⎞

⎠

,T=

⎛

⎝

OOO

OOK

OOO

⎞

⎠

, (6.89)

and an application of the rank identity (4.23) in Corollary 4.2.12 to D yields

the desired result as follows. Let (

J) be a minimizer on the right-hand side

of (4.23), where

I ⊆ Row(D)and

J ⊆ Col(D), for which we have

rank D =rankQ[

J] −|

I|−|

J|+2(n + m + l)

and rank T [

J] = 0. The structure of T allows us to assume that

I ⊇ X ∪Y

and

J ⊇ X ∪ U. Putting I = U \

I and J = Y \

J,wehave(I,J) ∈C

and

rank Q[

J]=rank



A − λI

B[X, I]

C[J, X] O



+ |U \ I| + |Y \ J|.

Therefore, we obtain

rank (A + BKC − λI

)=rank



A − λI

B[X, I]

C[J, X] O



As the above proof reveals, the content of Theorem 6.5.1 lies in a min-max

duality assertion that

max

K∈K

rank (A + BKC − λI

) = min

(I,J)∈C

rank



A − λI

B[X, I]

C[J, X] O



. (6.90)

This identity is observed by Tanino–Takahashi [309] in the special case of K

of the form (6.82).

We also mention the following result of Tarokh [311], with a simple proof

using a basic fact about mixed matrices.

Theorem 6.5.2. A complex number λ ∈ C isaﬁxedmodeof(A, B, C) with

respect to K of (6.85) if and only if



A − λI

B[X, I]

C[J, X] O



is singular for all

(I,J) such that K[I,J] is nonsingular.

6.5 Fixed Modes of Decentralized Systems 387

Proof. Application of Lemma 4.2.7 to the mixed matrix D = Q + T in (6.88)

and (6.89).

As a reﬁnement of the above theorem, Tanino–Takahashi [309] showed

max

K∈K

rank (A + BKC − λI

) = max

I,J



rank



A − λI

B[X, I]

C[J, X] O



−|I|

(6.91)

where the maximum on the right-hand side is taken over all (I,J) such that

K[I,J] is nonsingular. This identity can be derived similarly from Theorem

4.2.8 applied to the mixed matrix D = Q + T in (6.88) and (6.89).

Remark 6.5.3. Though both Theorem 6.5.1 and Theorem 6.5.2 are con-

cerned with combinatorial characterizations of ﬁxed modes, they are com-

plementary in the following sense. The former guarantees the existence of a

“certiﬁcate” (namely, (I,J) in the theorem) for λ being a ﬁxed mode, whereas

the latter (in its contraposition) for λ not being a ﬁxed mode. 2

Remark 6.5.4. In §6.4 we have discussed the controllability for (A, B). The

ﬁxed mode problem contains this as a special case. Given (A, B), consider

a ﬁxed mode problem with C = I

and K deﬁned by

= 1 for all (i, j).

Then, by a fundamental result in control theory (Wolovich [342]), (A, B)is

controllable if and only if (A, B, C) has no ﬁxed modes with respect to K. 2

6.5.2 Structurally Fixed Modes

The concept of a structurally ﬁxed mode is proposed by Sezer–

Siljak [294]

on the basis of the observation that some ﬁxed modes stem from an acciden-

tal matching of numerical values of system parameters and others from the

combinatorial structure of the system. For a system (A, B, C) we associate

a family S of systems that are “structurally equivalent” to (A, B, C), where

(

C) is said to be structurally equivalent to (A, B, C)if

B,and

C have

respectively the same zero/nonzero structure as that of A, B,andC. A sys-

tem (A, B, C) is said to have structurally ﬁxed modes if every (

C) ∈S

has ﬁxed modes. It is noted that considering the family S of structurally

equivalent systems is algebraically tantamount to considering a single system

in which all the nonzero entries of A, B,andC are algebraically indepen-

dent. See

Siljak [300, §1.6] and Trave–Titli–Tarras [320] for more account on

structurally ﬁxed modes.

Example 6.5.5. For a scalar system (A, B, C) = ((1), (0), (0)) we associate

a structured system (

C)=((a), (0)

, (0)) with an independent parameter

a. The system (A, B, C)hasaﬁxedmodeλ = 1 with respect to K = {(k) | k ∈

R}, and the structured system (

C)hasaﬁxedmodeλ = a. Accordingly,

the system (A, B, C) has a structurally ﬁxed mode. Note that the ﬁxed mode

of (

C) varies with a. 2

388 6. Theory and Application of Mixed Polynomial Matrices

The following theorem of Sezer–

Siljak [294] gives a combinatorial charac-

terization of the existence of structurally ﬁxed modes of a system (A, B, C).

The feedback structure is represented by a family K of matrices K subject

to an arbitrarily speciﬁed zero/nonzero structure.

Theorem 6.5.6. Asystem(A, B, C) has structurally ﬁxed modes with re-

spect to K of (6.85) if and only if either of the following two conditions is

satisﬁed, where C

is deﬁned in (6.86).

(i) There exists (I,J) ∈C

and a partition of X into disjoint subsets

, X

with X

= ∅ such that A[X

∪ X

]=O, A[X

]=O,

B[X

∪ X

,I]=O,andC[J, X

∪ X

]=O, that is, such that

A =

⎛

⎝

⎞

⎠

,B=

⎛

⎝

IU\ I

⎞

⎠

C =



Y \ JC



(ii) There exists (I,J) ∈C

such that

term-rank



AB[X,I]

C[J, X] O



≤ n − 1. (6.92)

Proof. This is proven later using Theorem 6.5.7 below. It may be noted that

the necessity of (ii) follows from Theorem 6.5.1.

The criteria given in the above theorem can be reformulated as follows

(Linnemann [175], Pichai–Sezer–

Siljak [269]). We represent the structure of

asystem(A, B, C) with feedback K by a directed graph G =(V,E). The

vertex set V and the arc set E are deﬁned by

V = X ∪ U ∪ Y, X = {x

, ···,x

},U= {u

, ···,u

},Y= {y

, ···,y

E = E

∪ E

= {(x

) | A

=0},E

= {(u

) | B

=0},

= {(x

) | C

=0},E

= {(y

) |

=0}.

Note that G is the graph associated with the matrix



ABO

OOK

COO



as in §2.2.1.

Theorem 6.5.7. Asystem(A, B, C) has no structurally ﬁxed modes with

respect to K of (6.85) if and only if both of the following two conditions are

satisﬁed:

(G1) Each vertex of X is contained in a strong component of G which in-

cludes an arc of E

6.5 Fixed Modes of Decentralized Systems 389

(G2) There exists a set of mutually disjoint cycles in G that covers the

vertices of X.

Proof. This will be proven later as a corollary of a more general result in

§6.5.3; see Remark 6.5.16.

The equivalence of Theorem 6.5.6 and Theorem 6.5.7 can be shown by

a fairly easy graph-theoretic argument. First, the condition (i) of Theorem

6.5.6 is easily seen to be equivalent to the violation of (G1) of Theorem 6.5.7.

Next, denote by D

the matrix D in (6.88) with λ = 0. The condition in (G2)

of Theorem 6.5.7 is equivalent to the term-nonsingularity of D

. Note that

(

J) is a cover of D

if and only if Y \

J ⊆

I, U \

I ⊆

J,(I,J) ∈C

and

(

I ∩ (X ∪ Y ),

J ∩ (X ∪ U)) is a cover of the matrix in (6.92) for I =

I ∩ U,

J =

J ∩ Y . Then the K¨onig–Egerv´ary theorem (Theorem 2.2.15) shows the

equivalence between the condition (ii) of Theorem 6.5.6 and the violation of

(G2) of Theorem 6.5.7.

The two theorems are certainly equivalent as above, and moreover both

show how to check for the existence of a structurally ﬁxed mode eﬃciently

using binary operations only. They are, however, complementary in the sense

that Theorem 6.5.6 guarantees a “certiﬁcate” for the existence of a struc-

turally ﬁxed mode whereas Theorem 6.5.7 for the nonexistence. See also Re-

mark 6.5.3.

Example 6.5.8. The conditions (G1) and (G2) in Theorem 6.5.7 do not

discriminate the existence of zero and nonzero ﬁxed modes. Consider, for

example, a scalar system (n = 1) with A = (0), B =(b), C =(c), and K =

(0). Obviously, this system has a (structurally) ﬁxed mode at zero, and no

nonzero ﬁxed mode. Neither (G1) nor (G2) in Theorem 6.5.7 is satisﬁed. Note

also that both of the conditions (i) and (ii) in Theorem 6.5.6 are satisﬁed. In

contrast, the matroid-theoretic method to be developed in the next subsection

will separate zero and nonzero ﬁxed modes. 2

Example 6.5.9. Consider a decentralized system (n = 6) with three local

stations described by

A =

⎛

⎜

⎝

0 a

0000

0 0 0000

0 0101

0 0 0000

0 0 0101

0 0 0000

⎞

⎟

⎠

,B=

⎛

⎜

⎝

000

0 b

000

00b

⎞

⎟

⎠

,K=

⎛

⎝

0000

00k

0000k

⎞

⎠

and C = I

, where {a

} is the set of independent parameters (see

Reinschke [278, Example 4] and the references cited therein for the origin of

this system). It can be veriﬁed that λ = 0 is a ﬁxed mode of all the systems

parametrized by {a

}. In this sense, the family parametrized

by {a

} has a structure that admits a ﬁxed mode. This fact,

390 6. Theory and Application of Mixed Polynomial Matrices

however, cannot be captured in the present formulation of structurally ﬁxed

modes, since λ = 0 is not a ﬁxed mode if the four entries of A having a

constant value of one are replaced by free parameters. Accordingly, the graph-

theoretic method of Theorem 6.5.7 leads us to the conclusion that this system

has no structurally ﬁxed mode. In contrast, the matroid-theoretic method to

be developed in the next subsection is capable of detecting this kind of ﬁxed

mode, as will be explained in Example 6.5.19. 2

6.5.3 Mixed Polynomial Matrix Formulation

Let us introduce a formulation of structurally ﬁxed modes, due to Murota

[209], which is more general and would be more realistic than the one de-

scribed in §6.5.2.

Let

A(s)=Q(s)+T (s) (6.93)

be an n ×n mixed polynomial matrix with respect to (K, F )=(Q, R) such

that Q(s) satisﬁes the stronger assumption

(MP-Q2) Every nonvanishing subdeterminant of Q(s) is a monomial

over K, i.e., of the form αs

with α ∈ K and an integer p.

We put R =Row(A)andC = Col(A). Let K be an n ×n generic matrix, the

nonzero entries of which are algebraically independent numbers in R. Then

(s)=A(s)+K = Q(s)+T (s)+K = Q(s)+T

(s) (6.94)

is a mixed polynomial matrix, where T

(s)=T (s)+K. We assume through-

out that A

(s) is nonsingular.

Denote by K the set of nonzero entries of K,andbyS the set of nonzero

coeﬃcients in T (s). Then K∪S is algebraically independent over Q. It should

be clear that assuming the algebraic independence of S is equivalent to re-

garding the members of S as independent parameters, and therefore to con-

sidering a family of systems parametrized by those parameters in S. A partic-

ular system in this family having algebraically independent parameter values

has a ﬁxed mode with respect to K if and only if each system parametrized

by S has a ﬁxed mode with respect to K. Note, however, the value of a ﬁxed

mode varies, in general, with the parameters in S.

We deﬁne the ﬁxed polynomial ψ(s) as the greatest common divisor in

C[s] of all det A

(s), where arbitrary values are substituted into K. Namely,

ψ(s)=gcd{det A

(s) | K ∈K} (6.95)

with the obvious understanding of the notation “K ∈K”. Also we call a

complex number λ ∈ C a ﬁxed mode if ψ(λ)=0.

6.5 Fixed Modes of Decentralized Systems 391

Remark 6.5.10. The structurally ﬁxed mode as formulated in §6.5.2 is a

special case of the present formulation. To see this, note the identity

det(A + BKC − sI

)=(−1)

m+l

det

⎛

⎝

A − sI

O −I

CO−I

⎞

⎠

and take

Q(s)=

⎛

⎝

−sI

O −I

OO−I

⎞

⎠

,T(s)=

⎛

⎝

ABO

OOO

COO

⎞

⎠

,K=

⎛

⎝

OOO

OOK

OOO

⎞

⎠

(6.96)

in the decomposition (6.94). Then S is equal to the set of nonzero entries of

A, B,andC,andK to the set of nonzero entries of K. 2

We shall derive a necessary and suﬃcient condition, of a combinatorial

nature, for the existence of ﬁxed modes with the aid of the CCF of LM-

matrices. The derived condition can be tested eﬃciently. The proposed algo-

rithm is suitable for practical applications in that it is free from numerical

diﬃculty of rounding errors and is guaranteed to run in polynomial time in

the size of the control system in question. The established criterion naturally

reduces to the graph-theoretic criterion of §6.5.2.

Regarding det A

(s) as a polynomial in (s, S, K)overQ, we consider the

decomposition into irreducible polynomials in Q[s, S, K]. As a consequence

of the assumption (MP-Q2), this is expressed (cf. Lemma 6.3.2) as

det A

(s)=αs



k∈Ψ

(s, S) ·



k∈Ψ

(s, S, K), (6.97)

where α ∈ Q \{0}, p is a nonnegative integer, ψ

(s, S) ∈ Q[s, S] \ Q[s]for

k ∈ Ψ

,andψ

(s, S, K) ∈ Q[s, S, K] \ Q[s, S]fork ∈ Ψ

. The index sets,

and Ψ

, classify the irreducible factors according to whether they do not

contain or do contain variables in K.

Lemma 6.5.11. The ﬁxed polynomial ψ(s) is given as

ψ(s)=αs



k∈Ψ

(s, S). (6.98)

Proof. This is easy to see.

The existence of a zero ﬁxed mode is easy to characterize.

Theorem 6.5.12. For nonsingular A

(s) of (6.94) satisfying (MP-Q2), the

following conditions are equivalent.

(i) λ =0is not a ﬁxed mode.

(ii) There exists (I,J) such that Q(0)[R \ I,C \ J] is nonsingular and

(T (0) + K)[I,J] is term-nonsingular.

(iii) There exists no (I,J) such that T (0)[I,J]=O, K[I,J]=O,and

rank Q(0)[I,J] ≤|I| + |J|−n − 1.