Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

412 7. Further Topics

In the case of α = 1 we cannot tell how small δ

(A) is, though we know for

sure that δ

(A) is strictly smaller than

(A) = 13.

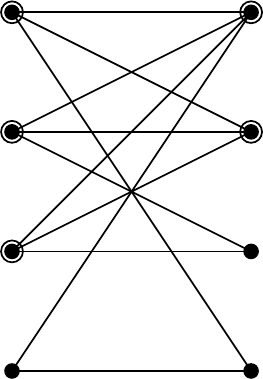
Fig. 7.3. Graph G

∗

(p, q) of tight arcs (Example 7.1.11, k =3)(: active vertex)

Next we consider the case of k = 2. We may choose the following optimal

dual variables:



=0,p



=1,p



=0,p



=0; p



=0,p



=1,p



=0,p



=0;

and q



=4,fromwhichwesee

(A)=π(p



) = 10. The tight coeﬃcient

matrix is given by

T (A; p



)=A

∗

⎛

⎜

⎝

•

α 100

• 1100

1100

0000

⎞

⎟

⎠

where the symbol • indicates the active row and column. Noting I

∗



}, J

∗



)={c

}, we see that the conditions (R2)–(R4) in Theorem 7.1.9

are satisﬁed for all values of α, whereas the ﬁrst condition (R1) is violated

when α = 1. Hence by Theorem 7.1.9 we see

(A)



(A) = 10 if α =1

≤

(A) − 1=9 ifα =1.

The exact values of δ

(A)andδ

(A) when α = 1 will be determined later in

Example 7.1.14. 2

7.1 Combinatorial Relaxation Algorithm 413

7.1.3 Transformation Towards Upper-tightness

When the matrix A(s) is not upper-tight, the combinatorial quantity

(A)

gives only an upper bound on δ

(A). We will show how to transform A(s)

eﬃciently to an upper-tight matrix through repeated biproper transforma-

tions (see §5.1.2 for the deﬁnition of biproper transformations). Note that

the Smith–McMillan form at inﬁnity (cf. §5.1.2) guarantees the existence of

such an upper-tight matrix, though this fact is not used below. For S = F (s),

F [s], F [1/s], or F [s, 1/s], we denote by M(S) the set of matrices with entries

in S.

Given A(s) ∈M(F (s)) with δ

(A) <

(A), we are to modify A(s)to

another matrix A



(s)=(A



(s)) such that

(P1) A



(s)=U(s)A(s)V (s), where U(s),V(s) ∈M(F [1/s]) and

det U(s), det V (s) ∈ F \{0},and

(P2)



) ≤

(A) − 1.

In particular, U(s)andV (s) are biproper matrices, and therefore δ



(A) by (5.5). When A(s) ∈M(F [s, 1/s]), the modiﬁed matrix A



(s)re-

mains in M(F [s, 1/s]) by the condition that U(s),V(s) ∈M(F [1/s]). It

should be obvious that we can get an upper-tight matrix by repeatedly ap-

plying this transformation.

Recall that a constant matrix A

∗

, called the tight coeﬃcient matrix, is

derived from A(s) with reference to an optimal dual variable (p, q), which is

assumed to be integer-valued. Since A(s) is not upper-tight, at least one of

the four rank conditions (R1)–(R4) in Theorem 7.1.9 is violated, whereas the

term-rank conditions (T1)–(T4) in Theorem 7.1.10 are satisﬁed. We consider

the modiﬁcation algorithm for each case.

If (R1) is violated:WehaverankA

∗

[R, C] <k≤ term-rank A

∗

[R, C].

Then there exists a nonsingular constant matrix U =(U

) (see the construc-

tion below) such that

term-rank (UA

∗

) ≤ k − 1. (7.22)

We transform A to A



(s)=U(s)A(s), (7.23)

where U(s)=(U

(s)) is given by

(s)=U

σ(h,i)

,σ(h, i)=p

− p

(7.24)

with reference to the dual variable p

=(p

| i ∈ R) associated with the

rows. The transformation matrix U(s) can be written also as

U(s) = diag (s; p

) · U · diag (s; −p

) (7.25)

using the notation (7.16).

We claim that the property (P2) is satisﬁed.

414 7. Further Topics

Lemma 7.1.12. (P2) is implied by (7.22).

Proof. The dual variable (p, q) is optimal for A. First we claim that (p, q)is

feasible for the modiﬁed matrix A



. By (7.15) and (7.25) we have

−q

· diag (s; −p

) · A



(s) · diag (s; −p

)

= U · s

−q

· diag (s; −p

) · A(s) · diag (s; −p

)

= U (A

∗

+ o(1)) = UA

∗

+ o(1),

which shows that w



− p

− q ≤ 0forw



= deg



(s).

Then (7.22) and Theorem 7.1.10 imply that (p, q) is not optimal for the

modiﬁed matrix A



, whereas it is for the original matrix A. Hence we have



) <π(p, q)=

(A).

By the integrality we ﬁnally obtain



) ≤

(A) − 1.

As to the property (P1) we easily see the following.

Lemma 7.1.13. (P1) is satisﬁed if [ U

=0 =⇒ p

≤ p

]. 2

The above statement says that U should be in a triangular form with

respect to the orderings of rows and columns determined by the dual vari-

able p

=(p

| i ∈ R) associated with the rows of A(s). Such U can be

constructed as follows.

Let τ : {1, ···,m}→R be a one-to-one correspondence such that [i ≤

h ⇒ p

Rτ(i)

≥ p

Rτ(h)

]. We denote by a

∗

∈ F

the row vector of A

∗

indexed by

i ∈ R.Let{a

∗

| i ∈ B} be the basis of row vectors of A

∗

that is constructed

by picking up the independent vectors from the sequence a

∗

τ(1)

, a

∗

τ(2)

, ···,

considered in this order. Also let {a

∗

| i ∈ D} be the set of vectors consisting

of the ﬁrst

d = m − k + 1 (7.26)

vectors in this sequence that do not belong to the basis. Hence B ⊆ R,

D ⊆ R, B ∩ D = ∅, |B| =rankA

∗

[R, C] <k,and|D| = d.

The row vector (U

| i ∈ R) of the matrix U is deﬁned for h ∈ D by the

relation

− a

∗



i∈B

∗

(h ∈ D), (7.27)

where U

=1,andU

=0ifi ∈ R \ (B ∪{h}). For h ∈ R \ D, it is deﬁned

to be the unit vector corresponding to h (i.e, U

= δ

), where δ

denotes

the Kronecker delta (δ

=1forh = i and = 0 otherwise). Then we have

=0ifτ

−1

(i) >τ

−1

(h), which guarantees the condition in Lemma 7.1.13.

The row vector of UA

∗

indexed by h ∈ D is zero by (7.27), and therefore

term-rank (UA

∗

) ≤ m − d = k − 1, as desired in (7.22).

7.1 Combinatorial Relaxation Algorithm 415

If (R2) is violated:WehaverankA

∗

,C] < |I

∗

| = term-rank A

∗

,C].

Then there exists a nonsingular constant matrix U =(U

) such that

term-rank (UA

∗

)[I

∗

,C] ≤|I

∗

|−1. (7.28)

As in the case of (R1) we transform A to A



by (7.23) with U(s) deﬁned by

(7.24). Lemma 7.1.13 remains true, insuring the property (P1). On the other

hand, (P2) is implied by (7.28). The proof is similar for Lemma 7.1.12; the

feasibility of (p, q)forA



is shown in the same manner, while the nonopti-

mality follows from (7.28) and Theorem 7.1.10.

The constant matrix U is constructed similarly as in the case (R1). How-

ever, in the sequence a

∗

τ(1)

, a

∗

τ(2)

, ···, we consider only those terms a

∗

τ(i)

which are the row vectors of the submatrix A

∗

,C] (i.e., those vectors with

τ(i) ∈ I

∗

). The independent vectors are chosen from this subsequence so

that {a

∗

| i ∈ B} may constitute the basis of row vectors of the submatrix

∗

,C]. Also we put d = 1 instead of (7.26). Namely, we pick up the ﬁrst

dependent vector in the subsequence. Then the row vector of UA

∗

indexed

by h ∈ D is zero by (7.27), and therefore term-rank (UA

∗

)[I

∗

,C] ≤|I

∗

|−1,

as required by (7.28).

If (R3) is violated:WehaverankA

∗

[R, J

∗

] < |J

∗

| = term-rank A

∗

[R, J

∗

The modiﬁcation in this case should be obvious from the one for the case

(R2). Just exchange the roles of the rows and the columns. This means in

particular that the matrix A is modiﬁed to A



by means of a transformation

of the form A



(s)=A(s)V (s) with

V (s) = diag (s; −p

) · V ·diag (s; p

), (7.29)

where V is a nonsingular constant matrix such that

term-rank (A

∗

V )[R, J

∗

] ≤|J

∗

|−1. (7.30)

If (R4) is violated:WehaverankA

∗

] < |I

∗

| + |J

∗

|−k ≤

term-rank A

∗

]. Then there exists a nonsingular constant matrix U =

) such that

term-rank (UA

∗

)[I

∗

] ≤|I

∗

| + |J

∗

|−k − 1. (7.31)

As in the case of (R1) we transform A to A



by (7.23) with U(s) deﬁned by

(7.24). Lemma 7.1.13 remains true, insuring the property (P1). On the other

hand, (P2) is implied by (7.31). The proof is similar for Lemma 7.1.12; the

feasibility of (p, q)forA



is shown in the same manner, while the nonopti-

mality follows from (7.31) and Theorem 7.1.10.

The constant matrix U is constructed similarly as in the case (R1). How-

ever, we order the row vectors {a

∗

] | i ∈ I

∗

} of the submatrix A

∗

]

into a sequence (a

∗

τ(i)

∗

] | i =1, 2, ···), and consider its subsequence consist-

ing of the vectors with τ(i) ∈ I

∗

. The independent vectors are chosen from

416 7. Further Topics

this subsequence so that {a

∗

] | i ∈ B} may constitute the basis of row

vectors of the submatrix A

∗

]. Also we put d = k +1−|J

∗

| instead of

(7.26), and deﬁne D ⊆ I

∗

to be the set of the ﬁrst d indices of the dependent

row vectors a

∗

The row vector (U

| i ∈ R) of the matrix U is deﬁned similarly except

that (7.27) is replaced by

−a

∗



i∈B

∗

](h ∈ D).

Then the row vector of (UA

∗

)[I

∗

] indexed by h ∈ D is zero, and therefore

term-rank (UA

∗

)[I

∗

] ≤|I

∗

|−d = |I

∗

|+|J

∗

|−k −1, as required by (7.31).

Example 7.1.14 (Continued from Example 7.1.11). Consider the case of

k =3,α = 1, where the matrix A(s) of Example 7.1.3 is not upper-tight,

since, as we have seen in Example 7.1.11, the tight coeﬃcient matrix A

∗

(7.21),

T (A; p, q)=A

∗

⎛

⎜

⎝

••

• 1102

• 1110

• 11−10

2001

⎞

⎟

⎠

does not satisfy the condition (R4) of Theorem 7.1.9. Namely, we have

rank A

∗

]=1< |I

∗

| + |J

∗

|−3 = 2 where I

∗

(p)={r

∗

(p)={c

} (indicated by •), and the optimal dual variable (p, q)is

given by (7.19) and (7.20).

We take the second row as the basis of the row vectors of A

∗

] (i.e.,

B = {r

}, D = {r

}, d =2)toget

U =

⎛

⎜

⎝

1 −100

0100

0 −110

0001

⎞

⎟

⎠

which, together with the dual variable p

of (7.19), yields

U(s) = diag (s

)·U ·diag (s

−2

−3

−2

⎛

⎜

⎝

1 −s

−1

0100

0 −s

−1

0001

⎞

⎟

⎠

Then the matrix A is modiﬁed to



(s)=U(s)A(s)=

⎛

⎜

⎝

0 −s

−1

−s

− s

+1 s

s −s

−1

−2s

−s

s 0 s +2

⎞

⎟

⎠

7.1 Combinatorial Relaxation Algorithm 417

This matrix turns out to be upper-tight for k = 3 with



)=δ



) = 12,

which is veriﬁed as follows.

We ﬁnd an optimal matching M

(4)

= {(r

), (r

)} of size 3

of weight w(M

(4)

) = 3 + 6 + 3 = 12 as well as the optimal dual variables



=1,p



=3,p



=0,p



=0; p



=0,p



=1,p



=1,p



=0;

and q



= 2, which shows



)=π(p



) = 12. The tight coeﬃcient matrix

T (A



; p



)=(A



)

∗

⎛

⎜

⎝

••

• 0002

• 1100

00−20

2000

⎞

⎟

⎠

satisﬁes the four conditions (R1)–(R4) in Theorem 7.1.9, where I

∗



}, J

∗



)={c

} (indicated by •). Hence



)=δ



). 2

7.1.4 Algorithm Description

Combining the procedures given above we obtain the following algorithm for

computing δ

(A)forA(s) ∈M(F (s)). For

max

(A) = max

i∈R,j∈C

deg

(s), (7.32)

min

(A)=−max

j∈C



i∈R

(degree of the denominator of A

(s)), (7.33)

we have k · w

min

(A) ≤ δ

(A) ≤

(A) ≤ k · w

max

(A)ifδ

(A) > −∞. Hence

the number of modiﬁcations of the matrix is bounded by

(0)

) − δ

(0)

) ≤ k(w

max

(0)

) − w

min

(0)

)),

where A

(0)

denotes the input matrix.

Algorithm for computing δ

(A)

Step 0

Deﬁne w

min

(A) as (7.33).

Step 1

(1) : Find a maximum weight k-matching M and integer-valued optimal

dual variables, p

(i ∈ R), p

(j ∈ C)andq,forG(A);

(A):=w(M)(

(A)=−∞ if no k-matching exists).

(2) : If

(A) <k· w

min

, then stop with δ

(A)=−∞.

Step 2

(1) : A

∗

:= lim

s→∞

−p

−q

(s)(i ∈ R, j ∈ C). [cf.(7.13)]

418 7. Further Topics

(2) : If the four conditions (R1)–(R4) in Theorem 7.1.9 are satisﬁed, then

stop with δ

(A)=

(A).

Step 3 [A is not upper-tight]

(1) : Modify the matrix A(s) as described in §7.1.3, according to which

of (R1)–(R4) is violated. (If (R1) is violated, for example, let U be

deﬁned by (7.27) and A(s) := diag (s; p

) · U · diag (s; −p

)A(s)).

(2) : Go to Step 1. 2

The stopping criterion in Step 1 (2) is to cope with the case of δ

(0)

−∞. In Step 2, we need row/column elimination operations on A

∗

. Though it

requires O(max(m

)) arithmetic operations in F in the worst case, it can

be done much faster since A

∗

is usually very sparse in practical applications.

Finally let us mention the probabilistic behavior of the algorithm. As

already noted in Theorem 7.1.1,

(A) diﬀers from δ

(A) only because of

accidental numerical cancellation. Let us ﬁx the structure (i.e., the position

of the nonzero coeﬃcients) of the input matrix A = A

(0)

and regard the

numerical values of coeﬃcients in R = F as real-valued random variables

with continuous distributions. Then we have

(A)=δ

(A) with probabil-

ity one, which means that Step 3 is performed only with null probability.

Since the worst-case time complexity for the weighted-matching problem is

bounded by O((m + n)

), we obtain the following statement, indicating the

practical eﬃciency of the proposed algorithm: The average time complexity

(in the above sense) of the proposed algorithm for a ﬁxed k is bounded by a

polynomial in m + n (e.g., (m + n)

Notes. The idea of the combinatorial relaxation algorithm was proposed

ﬁrst by Murota [212] for the Newton diagram of determinantal equations,

which was followed by Murota [219] (the degree of the determinant of (skew-

symmetric) polynomial matrices), Murota [220] (the degree of subdetermi-

nants), Iwata–Murota–Sakuta [147] (primal-dual type algorithm together

with comparative computational results), Iwata–Murota [146] (mixed poly-

nomial matrix formulation using valuated matroids), and Iwata [141] (matrix

pencil using strict equivalence). This section is based on Murota [220].

7.2 Combinatorial System Theory

This section is devoted to the description of a combinatorial analogue of the

dynamical system theory of Murota [202, 206, 211]. The theory is developed in

a matroid-theoretic framework by replacing the matrices A and B in the state-

space equations

x = Ax + Bu or x

k+1

= Ax

+ Bu

with bimatroids. The

main objective is to extend the combinatorial mathematical aspects in the

arguments of structural controllability, rather than to pursue physical faith in

the structural approach. Combinatorial counterparts are given to a number of

7.2 Combinatorial System Theory 419

fundamental concepts such as controllability in the conventional system the-

ory, revealing the combinatorial nature of some fundamental results in the

conventional system theory. However, the present theory is not a direct gen-

eralization of the existing “generic” approach, mainly because of the possible

discrepancy between the matrix multiplication and bimatroid multiplication.

Here the discrepancy means the failure of the relation L(A)∗L(B)=L(A·B)

for matrices A and B, where L(·) denotes the bimatroid deﬁned by a matrix.

7.2.1 Deﬁnition of Combinatorial Dynamical Systems

A combinatorial analogue of the dynamical system

k+1

= Ax

+ Bu

(7.34)

is obtained by replacing the matrices A and B with two bimatroids. To be

more precise, a combinatorial dynamical system (to be abbreviated as CDS)

is a pair (A, B) of bimatroids such that Row(A) = Col(A)=Row(B)(≡ S)

and that S and Col(B)(≡ P ) are mutually disjoint: A =(S, S, Λ(A),α),

B =(S, P, Λ(B),β), where α and β are birank functions. The set S is called

the state set, whereas P is the input set. A bimatroid F is called a state

feedback if Row(F)=P and Col(F)=S.

As a counterpart of (7.34), we consider

k+1

∪ U

) ∈ Λ(A ∨ B),X

k+1

⊆ S, U

⊆ P. (7.35)

By deﬁnition, this means that X

k+1

can be partitioned into two disjoint parts,

say X



k+1

and X



k+1

, such that (X



k+1

) ∈ Λ(A) and (X



k+1

) ∈ Λ(B).

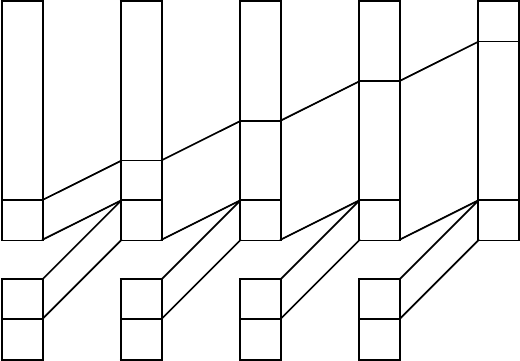
See Fig. 7.4 and compare it with the dynamic graph introduced in §2.2.1

(see also Fig. 2.5). The equation (7.35) will be referred to as the state-space

equation for the CDS.

An input is a sequence (U

)

K−1

k=0

=(U

| k =0, 1, ···,K − 1),U

⊆ P .

We say that a sequence (X

)

k=0

=(X

| k =0, 1, ···,K),X

⊆ S,isa

trajectory compatible with (U

)

K−1

k=0

if (7.35) holds for k =0, 1, ···,K−1. An

input is said to be admissible for (X



,X) if there exists a trajectory (X

)

k=0

compatible with it such that X

= X



and X

= X.Put

)={X

⊆ S | some (U

)

k−1

i=0

is admissible for (X

)}, (7.36)

RS(X

∞



k=0

). (7.37)

Then we say that X (⊆ S)isreachable at time k (≥ 0) from X

(⊆ S)if

X ∈ RS

), and that a CDS is reachable if {x}∈RS(∅)for∀x ∈ S.We

also say that a CDS is control lable if RS(∅)=2

420 7. Further Topics

(0)

(1)





(1)

(2)





(2)

(3)





(3)

(4)





Fig. 7.4. Combinatorial dynamical system

7.2.2 Power Products

We ﬁrst consider an “autonomous” system in which input bimatroid B is

trivial (of rank zero). In this case the state-space equation (7.35) reduces to

k+1

) ∈ Λ(A),X

k+1

⊆ S. (7.38)

In other words, we investigate the power products of a single bimatroid A

such that Row(A) = Col(A).

Since Row(A) = Col(A), we can think of the product of A with itself.

We deﬁne A

recursively by A

= A

k−1

∗ A = A ∗ A

k−1

for k =1, 2, ···,

where, for convenience, we put A

=(S, S, Λ(A

)) with Λ(A

)={(X, X) |

X ⊆ S}. For an autonomous system,



⊆S

) agrees with the family

of independent sets of RM(A

), which we are interested in.

Remark 7.2.1. Even in the special case where A arises from a generic ma-

trix A with independent nonzero entries, the power products of A = L(A)

do not agree with the bimatroids associated with the power products of A,

i.e., L(A

) =(L(A))

. In fact, for

7.2 Combinatorial System Theory 421

A =

00t

0 t

0000

0 t

000

000t

where t

(i =1, ···, 6) are indeterminates, the 2 × 2 submatrix of A

with

row set {x

} and column set {x

} is singular, i.e., ({x

}, {x

}) ∈

Λ(L(A

)), whereas ({x

}, {x

}) ∈ Λ(L(A)

). 2

In spite of such discrepancy between L(A

)andL(A)

in the families of

the linked pairs, they share the same rank (=the maximum size of linked

pairs), as is stated in the following theorem of Poljak [270].

Theorem 7.2.2. rank (L(A

)) = rank (L(A)

) for a square generic matrix

Proof. See Poljak [270].

Fundamental properties of the power products of a bimatroid are stated

in the following two theorems shown by Murota [211]. The ﬁrst theorem

reveals that the sequence r(A

) = rank (A

), k =0, 1, 2, ···,isconvexand

nonincreasing.

Theorem 7.2.3. Let A be a bimatroid with Row(A) = Col(A)=S.

(1) r(A

k−1

) − r(A

) ≥ r(A

) − r(A

k+1

),k=1, 2, ···.

(2) There exists τ = τ(A)(0≤ τ ≤|S|) such that

r(A

) >r(A

) > ···>r(A

τ−1

) >r(A

)=r(A

),k= τ +1,τ +2, ···.

Proof. (1) This follows from Theorem 2.3.55 with L

= L

= A and L

k−1

(2) First note the obvious relation: r(A

) ≥ r(A

k+1

). Let τ be the small-

est k such that the equality holds, where τ ≤|S| since 0 ≤ r(A

) ≤

r(A

) − τ = |S|−τ. Then (1) implies that the equality must hold for all

k ≥ τ.

The integer τ = τ(A) above is called the transition index of A.Wesym-

bolically write r(A

∞

)forr(A

) though the limit of A

(as k →∞) may not

exist.

The ranks of the associated row and column matroids, RM(A

)and

CM(A

), satisfy similar inequalities, since rank (A

) = rank (RM(A

)) =

rank (CM(A

)). The following theorem establishes a stronger assertion than

the inequality of Theorem 7.2.3(2) above. It claims that the sequences of

{RM(A

)}

and {CM(A

)}

have nice nesting structures and consequently

their limits do exist, which will be denoted by RM(A

∞

)andCM(A

∞