Murota K. Matrices and Matroids for Systems Analysis
Подождите немного. Документ загружается.


392 6. Theory and Application of Mixed Polynomial Matrices
Proof. The equivalence of (i) to the nonsingularity of A
K
(0) is obvious. The
equivalence to (ii) and (iii) are by Lemma 4.2.7 and by (4.23) in Corollary
4.2.12.
The multiplicity of the zero fixed mode, the exponent p in (6.97), is equal
to ord
s
det A
K
(s), which can be characterized in terms of an independent
assignment problem (weighted matroid intersection problem) as in §6.2.4 (see
Remark 6.2.3 and Remark 6.2.10). Recall the notation ord
s
for the minimum
degree in s of a nonzero term in a polynomial introduced in (2.1). To be
specific, we consider, as in (6.55), an LM-polynomial matrix
˜
A
K
(s)=
˜
A
K
(s; t)=
I
n
Q(s)
−diag (t
1
, ···,t
n
) T
K
(s)
=
˜
Q(s)
˜
T
K
(s; t)
(6.99)
associated with A
K
(s), where t
1
, ···,t
n
are new indeterminates and t =
(t
1
, ···,t
n
). Put
˜
C = Col(
˜
A
K
) R ∪ C. With reference to (6.4) we define
ζ :
˜
C → Z by
ζ(j)=
−r
j
(j ∈ R)
−c
j
(j ∈ C)
(6.100)
as well as the usual convention ζ(J)=
j∈J
ζ(j)forJ ⊆
˜
C.ForJ ⊆
˜
C
such that
˜
T
K
[Row(
˜
T
K
),J] is term-nonsingular, we denote by η(J) the lowest
degree in s of a nonzero term in det
˜
T
K
[Row(
˜
T
K
),J]. Note that η(J) admits
a combinatorial expression, namely (cf. (6.13)),
η(J) = min{w(M) | M: n-matching with ∂
−
M = J in G
˜
T
}, (6.101)
where G
˜
T
=(Row(
˜
T
K
),
˜
C; E
˜
T
) is a bipartite graph with arc set E
˜
T
= {(i, j) |
i ∈ Row(
˜
T
K
),j ∈
˜
C,(
˜
T
K
)
ij
=0} and w(M)=
(i,j)∈M
ord
s
(
˜
T
K
)
ij
.Alsowe
define
J = {J ⊆
˜
C |
˜
Q[Row(
˜
Q),
˜
C \ J]: nonsingular,
˜
T
K
[Row(
˜
T
K
),J]: term-nonsingular}. (6.102)
Theorem 6.5.13. For nonsingular A
K
(s) of (6.94) satisfying (MP-Q2), the
multiplicity p of the zero fixed mode is given by
p = min{ζ(
˜
C \ J)+η(J) | J ∈J}−ζ(R).
Proof. This is a straightforward adaptation of Theorem 6.2.5.
On the basis of this theorem, the multiplicity of the zero fixed mode can
be computed efficiently by a variant of the algorithm in §6.2.6.
The nonzero fixed modes can be treated by means of the CCF of the LM-
polynomial matrix
˜
A
K
(s). This is based on the fact (Theorem 4.5.9) that the
CCF corresponds to the decomposition of the determinant into irreducible
factors.
6.5 Fixed Modes of Decentralized Systems 393
Regarding
˜
A
K
(s) as an LM-matrix with respect to (Q[s], R(s)) we may
think of its block-triangular form (“CCF over a ring”) in the sense of Theorem
4.4.19, which is obtained from
˜
A
K
(s) through a unimodular transformation
over Q[s]. Let
ˆ
A
K
(s)and
¯
A
K
(s) be the block-triangular matrix and the
CCF of
˜
A
K
(s) as in Theorem 4.4.19. The families of the row sets and the
column sets in the CCF are denoted respectively by {
¯
R
k
| k =1, ···,b} and
{
¯
C
k
| k =1, ···,b}, and the square diagonal blocks by
¯
A
k
=
¯
Q
k
¯
T
k
=
¯
A
K
[
¯
R
k
,
¯
C
k
],k=1, ···,b.
Note that
ˆ
A
K
(s)and
¯
A
K
(s) have identical diagonal blocks, though they may
differ in the upper-triangular part. Similarly to (6.102) we define
J
k
= {J ⊆
¯
C
k
|
¯
Q
k
[Row(
¯
Q
k
),
¯
C
k
\ J]: nonsingular,
¯
T
k
[Row(
¯
T
k
),J]: term-nonsingular},k=1, ···,b.
For J ⊆
¯
C
k
such that
¯
T
k
[Row(
¯
T
k
),J] is term-nonsingular, we denote by
ξ
k
(J)andη
k
(J) the highest and lowest degrees in s of a nonzero term in
det
¯
T
k
[Row(
¯
T
k
),J]. Note that ξ
k
(J)andη
k
(J) can be expressed in terms of
weighted-matching problems, just as (6.101).
To identify the nonzero fixed modes, we classify the diagonal blocks into
three categories by defining three index sets
¯
Ψ
0
= {k |
¯
A
k
contains no variable of S∪K}, (6.103)
¯
Ψ
1
= {k |
¯
A
k
contains a variable of S and no variable of K}, (6.104)
¯
Ψ
2
= {k |
¯
A
k
contains a variable of K}. (6.105)
Theorem 6.5.14. For nonsingular A
K
(s) of (6.94) satisfying (MP-Q2), the
number of nonzero fixed modes is given by
k∈
¯
Ψ
1
max{ζ(
¯
C
k
\ J)+ξ
k
(J) | J ∈J
k
}−min{ζ(
¯
C
k
\ J)+η
k
(J) | J ∈J
k
}
.
Hence there exist no nonzero fixed modes if and only if
max{ζ(
¯
C
k
\J)+ξ
k
(J) | J ∈J
k
} = min{ζ(
¯
C
k
\J)+η
k
(J) | J ∈J
k
} (6.106)
for each k ∈
¯
Ψ
1
.
Proof. It follows from (6.99) that
det A
K
(s) = det
˜
A
K
(s;1), (6.107)
where
˜
A
K
(s;1) =
˜
A
K
(s; t)
8
8
8
t
1
=···=t
n
=1
. On the other hand, we have

394 6. Theory and Application of Mixed Polynomial Matrices
det
˜
A
K
(s; t) = det
ˆ
A
K
(s; t) = det
¯
A
K
(s; t)=
b
k=1
det
¯
A
k
(s; t), (6.108)
where the first equality may be assumed by the fact that
ˆ
A
K
(s; t) is obtained
form
˜
A
K
(s; t) through a unimodular transformation over Q[s].
According to Theorem 4.5.9 the expression (6.108) gives a decomposition
into irreducible factors in the ring Q(s)[S, K,t]. In view of Lemma 6.3.2 we
see further that, for each k, det
¯
A
k
(s; t) is a product of a monomial in s and an
irreducible polynomial in Q[s, S, K,t]. This statement needs only a marginal
modification even after the substitution of t
1
= ··· = t
n
= 1. Namely, we
claim that, for k =1, ···,b,wehave
det
¯
A
k
(s;1) = ρ
k
(s) ·
¯
ψ
k
(s, S, K), (6.109)
where ρ
k
(s) ∈ Q[s] is a monomial in s,and
¯
ψ
k
(s, S, K) ∈ Q[s, S, K] \ Q[s]is
irreducible in Q[s, S, K].
The proof of (6.109) is easy. Denote by T
i
the set of elements of T≡
S∪Kcontained in the row of
˜
T
K
(s; t) corresponding to t
i
(i =1, ···,n).
Also denote det
¯
A
k
(s; t)byf
k
(T
1
, ···, T
n
; t
1
, ···,t
n
), which is irreducible in
Q(s)[T
1
, ···, T
n
,t
1
, ···,t
n
] by Theorem 4.5.6. We see
f
k
(T
1
, ···, T
n
; t
1
, ···,t
n
)=
⎛
⎝
i∈Row(
¯
T
k
)
t
i
⎞
⎠
· f
k
(T
1
/t
1
, ···, T
n
/t
n
;1, ···, 1),
where T
i
/t
i
means substituting a/t
i
for each indeterminate a ∈T
i
. This
expression implies that det
¯
A
k
(s; 1) is irreducible in Q(s)[S, K], which, with
Lemma 6.3.2, completes the proof of (6.109).
With reference to (6.97), a combination of (6.107), (6.108), and (6.109)
shows
k∈Ψ
1
ψ
k
(s, S)=
k∈
¯
Ψ
1
¯
ψ
k
(s, S),
k∈Ψ
2
ψ
k
(s, S, K)=
k∈
¯
Ψ
2
¯
ψ
k
(s, S, K).
In particular, the first expression above gives the nonmonomial part of the
fixed polynomial in Lemma 6.5.11. Finally we note
deg
s
¯
ψ
k
(s)=max{ζ(
¯
C
k
\J)+ξ
k
(J) | J ∈J
k
}−min{ζ(
¯
C
k
\J)+η
k
(J) | J ∈J
k
},
which is a corollary of Theorem 6.2.5.
On the basis of the combinatorial characterization of fixed modes in Theo-
rem 6.5.12 and Theorem 6.5.14, an efficient algorithm for testing the existence
of zero/nonzero fixed modes is designed in the next section.
6.5 Fixed Modes of Decentralized Systems 395
6.5.4 Algorithm
In this section we describe an efficient algorithm to check for the existence of
nonzero fixed modes on the basis of Theorem 6.5.14, whereas the algorithm
of §4.2.4 for computing the rank of an LM-matrix can be utilized readily for
the zero fixed mode by Theorem 6.5.12. The basic idea of the algorithm for
nonzero fixed modes is the same as that for nonzero uncontrollable modes in
§6.4.4.
A concrete description of the algorithm for the condition (6.106) follows.
We use an auxiliary network N =(V,E,γ) with underlying graph G =(V,E)
and length function γ : E → Z, in a way consistent with §4.2.4. The vertex
set V is defined as
V = V
Q
∪ V
T
=(R
Q
∪ C
Q
) ∪ (R
T
∪ C
T
),
where R
Q
=Row(Q), C
Q
= Col(Q), R
T
=Row(T ), C
T
= Col(T ), V
Q
=
R
Q
∪ C
Q
,andV
T
= R
T
∪ C
T
. The arc set E consists of six disjoint parts,
E = E
TQ
∪ E
QT
∪ E
Q
∪ E
T
∪ E
K
∪ E
M
,
to be defined below. We denote by ϕ
Q
: R ∪C → R
Q
∪C
Q
and ϕ
T
: R ∪C →
R
T
∪ C
T
the obvious one-to-one correspondences.
Let
ˆ
I ⊆ R and
ˆ
J ⊆ C be such that Q(1)[R \
ˆ
I,C \
ˆ
J] is nonsingular and
T
K
[
ˆ
I,
ˆ
J] is term-nonsingular, where such (
ˆ
I,
ˆ
J) exists by the nonsingularity
of A
K
(1) and Lemma 4.2.7. We define
E
TQ
= {(ϕ
T
(i),ϕ
Q
(i)) | i ∈
ˆ
I}∪{(ϕ
T
(j),ϕ
Q
(j)) | j ∈ C \
ˆ
J},
E
QT
= {(ϕ
Q
(i),ϕ
T
(i)) | i ∈ R \
ˆ
I}∪{(ϕ
Q
(j),ϕ
T
(j)) | j ∈
ˆ
J}.
Let P be the pivotal transform of Q = Q(1) with pivot
ˆ
Q ≡ Q[R \
ˆ
I,C \
ˆ
J]
(cf. (6.76)), where Row(P )=(C \
ˆ
J) ∪
ˆ
I and Col(P)=(R \
ˆ
I) ∪
ˆ
J. Note that
P is a constant matrix free from s. With reference to P we define
E
Q
= {(ϕ
Q
(i),ϕ
Q
(j)) | P
ij
=0,i∈ (C \
ˆ
J) ∪
ˆ
I,j ∈ (R \
ˆ
I) ∪
ˆ
J}.
The structure of T
K
(s)=T (s)+K is represented by E
T
, E
K
,andE
M
.
For each nonzero entry T
ij
(s)ofT (s) we consider a pair of parallel arcs a
0
ij
and a
1
ij
with ∂
+
a
0
ij
= ∂
+
a
1
ij
= ϕ
T
(i) ∈ R
T
and ∂
−
a
0
ij
= ∂
−
a
1
ij
= ϕ
T
(j) ∈ C
T
.
Putting
E
0
T
= {a
0
ij
| T
ij
=0,i∈ R, j ∈ C},E
1
T
= {a
1
ij
| T
ij
=0,i∈ R, j ∈ C},
we define E
T
= E
0
T
∪ E
1
T
and
E
K
= {(ϕ
T
(i),ϕ
T
(j)) | K
ij
=0,i∈ R, j ∈ C}.
Since T
K
[
ˆ
I,
ˆ
J] is term-nonsingular, the bipartite graph (R
T
,C
T
; E
T
∪ E
K
)
with vertex set R
T
∪C
T
and arc set E
T
∪E
K
has a matching M (⊆ E
T
∪E
K
)

396 6. Theory and Application of Mixed Polynomial Matrices
such that |M| = |
ˆ
I|(= |
ˆ
J|), ϕ
T
(
ˆ
I)=∂
+
M,andϕ
T
(
ˆ
J)=∂
−
M. We define
E
M
as the set of reoriented arcs of M, i.e.,
E
M
= {¯a | a ∈ M},
where ¯a denotes the reorientation of a.
The length function γ : E → Z is defined with reference to r
i
and c
i
(i =1, ···,n) of (6.4) as
γ(a)=
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
−r
i
if a =(ϕ
T
(i),ϕ
Q
(i)) ∈ E
TQ
,i∈
ˆ
I,
−c
j
if a =(ϕ
T
(j),ϕ
Q
(j)) ∈ E
TQ
,j∈ C \
ˆ
J,
r
i
if a =(ϕ
Q
(i),ϕ
T
(i)) ∈ E
QT
,i∈ R \
ˆ
I,
c
j
if a =(ϕ
Q
(j),ϕ
T
(j)) ∈ E
QT
,j∈
ˆ
J,
0ifa ∈ E
Q
∪ E
K
,
−ord
s
T
ij
(s)if a ∈ E
0
T
,
−deg
s
T
ij
(s)if a ∈ E
1
T
,
−γ(a
)ifa ∈ E
M
is the reorientation of a
∈ M.
For a nonzero entry T
ij
(s)ofT (s) with ord
s
T
ij
(s) = deg
s
T
ij
(s) (which is the
case if T
ij
(s) is a monomial in s), the pair of arcs, having the same length,
may be replaced by a single arc of the same length.
We are now ready to rephrase the condition (6.106) in terms of the net-
work N =(G, γ). Note that the strong components of G correspond to
diagonal blocks of the CCF of
˜
A
K
. For each strong component of G,say
ˆ
G =(
ˆ
V,
ˆ
E), we consider the condition that the sum of the lengths γ(a) along
any directed cycle in
ˆ
G is equal to zero (cf. (6.78)). Since
ˆ
G is strongly con-
nected, this condition is equivalent, by Theorem 2.2.35(2), to the existence
of a potential function π :
ˆ
V → Z such that
γ(a)=π(∂
−
a) − π(∂
+
a)(∀a ∈
ˆ
E). (6.110)
Theorem 6.5.15. For nonsingular A
K
(s) of (6.94) satisfying (MP-Q2),
there exist no nonzero fixed modes if and only if each strong component of
G either contains an arc of E
K
or admits a potential function π such that
(6.110) holds.
Proof. For simplicity of notation let us assume that G itself is a strong com-
ponent that does not contain an arc of E
K
. We also assume for simplicity of
argument that each T
ij
(s) is a monomial in s so that each pair of parallel
arcs in E
T
is replaced by a single arcs. Consider the independent assignment
problem as in §6.2 to compute deg
s
det
˜
A
K
(s)for
˜
A
K
(s) of (6.99). The rest
of the proof is the same as that of Theorem 6.4.18.
The overall computational complexity for testing for the existence of
fixed modes on the basis of Theorem 6.5.12 and Theorem 6.5.15 is domi-
nated by that for the construction of the graph G and therefore bounded by
O(n
3
log n). Note that the decomposition of G into strong components can be
6.5 Fixed Modes of Decentralized Systems 397
done in O(|E|) time and the potential function of (6.110) for a strong com-
ponent
ˆ
G =(
ˆ
V,
ˆ
E), if any, can be found in time of O(|
ˆ
E|) by the procedure
of Remark 6.4.19. It should be emphasized here that the whole algorithm
involves only pivoting operations on the matrix Q(1), the entries of which
are rational numbers (simple numbers such as ±1 in practical applications).
Remark 6.5.16. The graph-theoretic criterion in Theorem 6.5.7 can be
derived from Theorem 6.5.12 and Theorem 6.5.15 applied to the matrix
D(s)=Q(s)+T (s)+K defined by (6.96) in Remark 6.5.10. Recall (cf. (6.88))
that both Row(D) and Col(D) have a natural one-to-one correspondence
with X ∪ U ∪ Y , to be denoted by ν
R
:Row(D) → X ∪ U ∪ Y and
ν
C
: Col(D) → X ∪ U ∪ Y . Note also that Q(s) satisfies (MP-Q2) with
r
i
=
1(ν
R
(i) ∈ X)
0(ν
R
(i) ∈ U ∪ Y ),
c
j
=0 (j ∈ Col(D)).
In considering nonzero fixed modes we may take (
ˆ
I,
ˆ
J)=(∅, ∅) since Q(s)is
nonsingular. The auxiliary network N =(G, γ)for(
ˆ
I,
ˆ
J)=(∅, ∅)iseasyto
identify. We have
E
TQ
= {(ϕ
T
(j),ϕ
Q
(j)) | j ∈ Col(D)},
E
QT
= {(ϕ
Q
(i),ϕ
T
(i)) | i ∈ Row(D)},
E
Q
= {(ϕ
Q
(j),ϕ
Q
(i)) | ν
R
(i)=ν
C
(j),i∈ Row(D),j ∈ Col(D)},
E
T
= {(ϕ
T
(i),ϕ
T
(j)) | T
ij
=0},
E
K
= {(ϕ
T
(i),ϕ
T
(j)) | K
ij
=0},
E
M
= ∅,
and γ(a)=1ifa =(ϕ
Q
(i),ϕ
T
(i)) ∈ E
QT
with ν
R
(i) ∈ X,andγ(a)=0
otherwise. Let us call an arc a with γ(a)=1acritical arc. A critical arc
corresponds to an element of X. It is easy to see that a strong component of
G (of N) containing a critical arc cannot admit a potential function.
We mean by (M1) the condition that each strong component of G either
contains an arc of E
K
or admits a potential function π such that (6.110)
holds, and by (M2) the condition of nonsingularity of D(0). We also refer to
the conditions (G1) and (G2) in Theorem 6.5.7.
The equivalence of (G2) and (M2) is easy to see. Also the implication,
(G1) =⇒ (M1), is easy to see. The converse is not always true (see Example
6.5.18). Under the condition (M2), however, every critical arc is contained in
a strong component of G, and consequently, the converse, (M1) =⇒ (G1), is
also true. Thus we have shown [(M2) ⇐⇒ (G2)], [(G1) =⇒ (M1)], and [(M1),
(M2) =⇒ (G1)], proving [(M1), (M2) ⇐⇒ (G1), (G2)]. It is emphasized,
however, that (G1) alone does not correspond to the nonexistence of nonzero
fixed modes, as we have seen in Example 6.5.8. 2

398 6. Theory and Application of Mixed Polynomial Matrices
6.5.5 Examples
Example 6.5.17. The algorithm described in §6.5.4 as well as the derivation
in §6.5.3 is illustrated here by means of an example. Consider a 9 × 9 mixed
polynomial matrix A
K
(s)=Q(s)+T (s)+K of (6.94) with Q(s)andT (s)
given by
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
x
9
w
1
101000000
w
2
001000000
w
3
000000000
w
4
−10−10 0 0 000
w
5
00001 s 0 s 0
w
6
1010−1 −ss 00
w
7
000000000
w
8
−s 0 −s 0 0 0 001
w
9
000000000
,
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
x
9
00 0000000
0 sf
1
0000a
1
00
0 a
2
sf
2
a
3
a
4
0000
00 0000000
00 000000a
5
00 00000a
6
0
00 00000a
7
a
8
00 0000000
00 00a
9
sf
3
000
,
and
K =
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
x
9
w
1
00000000k
1
w
2
000000000
w
3
000000000
w
4
000k
2
00000
w
5
000000k
3
00
w
6
000000000
w
7
000000k
4
00
w
8
000000000
w
9
000000000
.
The assumption (MP-Q2) is satisfied, where (6.4) holds true with
(r
1
, ···,r
9
)=(0, 0, 0, 0, 0, 0, 0, 1, 0), (c
1
, ···,c
9
)=(0, 0, 0, 0, 0, −1, −1, −1, 1).
Note that S = {a
1
, ···,a
9
}∪{f
1
, ···,f
3
} and K = {k
1
, ···,k
4
}.
By direct calculation we obtain
det A
K
(s)=[s] ×
(a
9
− f
3
)(f
1
f
2
s
2
− a
2
)
×[k
2
(k
1
s + 1)(a
7
s − k
4
s + a
7
k
3
− a
6
k
4
)] ,
where the brackets [ ] correspond to the three parts in (6.97). It follows from
Lemma 6.5.11 that the fixed polynomial is given by ψ(s)=(a
9
− f
3
) · s ·
(f
1
f
2
s
2
− a
2
), where α =(a
9
− f
3
)andp = 1 in (6.98).
The associated LM-polynomial matrix
˜
A
K
(s) of (6.99) is given by
6.5 Fixed Modes of Decentralized Systems 399
w
1
w
2
w
3
w
4
w
5
w
6
w
7
w
8
w
9
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
x
9
1101000000
1001000000
1000000000
1 −10−10 0 0 0 0 0
100001s 0 s 0
11010−1 −ss 00
1000000000
1 −s 0 −s 00 0001
1000000000
−t
1
00000000k
1
−t
2
0 sf
1
000 0a
1
00
−t
3
0 a
2
sf
2
a
3
a
4
0000
−t
4
000k
2
00000
−t
5
000000k
3
0 a
5
−t
6
0000000a
6
0
−t
7
000000k
4
a
7
a
8
−t
8
000000000
−t
9
0000a
9
sf
3
000
.
The CCF
¯
A
K
(s), being identical with the block-triangular matrix
ˆ
A
K
(s)in
this example, is given by
¯
C
1
¯
C
2
¯
C
3
¯
C
4
¯
C
5
¯
C
6
¯
C
7
¯
C
8
¯
C
9
¯
C
10
¯
C
11
x
1
w
2
x
2
x
3
w
3
x
4
w
4
x
5
x
6
w
9
w
5
w
6
x
7
x
8
w
7
w
1
x
9
w
8
1 11
101
−t
2
sf
1
0 a
1
0 a
2
sf
2
−t
3
a
3
a
4
1 1
k
2
−t
4
1
−1 −s 1 s −1
a
9
sf
3
−t
9
1
11ss −1
0 −t
6
0 a
6
−t
5
0 k
3
0 a
5
00k
4
a
7
−t
7
a
8
1
s 1 1
−t
1
k
1
−t
8
.
The CCF has 11 blocks of column sets:
¯
C
1
= {x
1
},
¯
C
2
= {w
2
,x
2
,x
3
},
¯
C
3
= {w
3
},
¯
C
4
= {x
4
},
¯
C
5
= {w
4
},
¯
C
6
= {x
5
,x
6
},
¯
C
7
= {w
9
},
¯
C
8
=
{w
5
,w
6
,x
7
,x
8
},
¯
C
9
= {w
7
},
¯
C
10
= {w
1
,x
9
},
¯
C
11
= {w
8
}. The index sets
of (6.103)–(6.105) are given by
¯
Ψ
0
= {1, 3, 5, 7, 9, 11},
¯
Ψ
1
= {2, 6},and
¯
Ψ
2
= {4, 8, 10},and
¯
ψ
k
(s) of (6.109) for k ∈
¯
Ψ
1
∪
¯
Ψ
2
are:
¯
ψ
2
(s)=(f
1
f
2
s
2
− a
2
),
¯
ψ
6
(s)=(a
9
− f
3
);
¯
ψ
4
(s)=k
2
,
¯
ψ
8
(s)=(a
7
s − k
4
s + a
7
k
3
− a
6
k
4
),
¯
ψ
10
(s)=(k
1
s +1).

400 6. Theory and Application of Mixed Polynomial Matrices
Note also that det
¯
A
6
= s ·
¯
ψ
6
.
We now illustrate the algorithm of §6.5.4. Suppose we have found
ˆ
I =
{w
2
,w
3
,w
4
,w
5
,w
7
,w
9
},
ˆ
J = {x
2
,x
3
,x
4
,x
6
,x
7
,x
8
}, and a matching M =
{a
7
,f
1
,f
2
,f
3
,k
2
,k
3
} by applying the algorithm of §4.2.4 to A
K
(1) above.
Then the matrix P of (6.76) is given by
P =
w
1
w
6
w
8
x
2
x
3
x
4
x
6
x
7
x
8
x
1
1000100 0 0
x
5
1 −10 0001−10
x
9
1010000 0 0
w
2
0000100 0 0
w
3
0000000 0 0
w
4
1000000 0 0
w
5
−11 0 0000 1 1
w
7
0000000 0 0
w
9
0000000 0 0
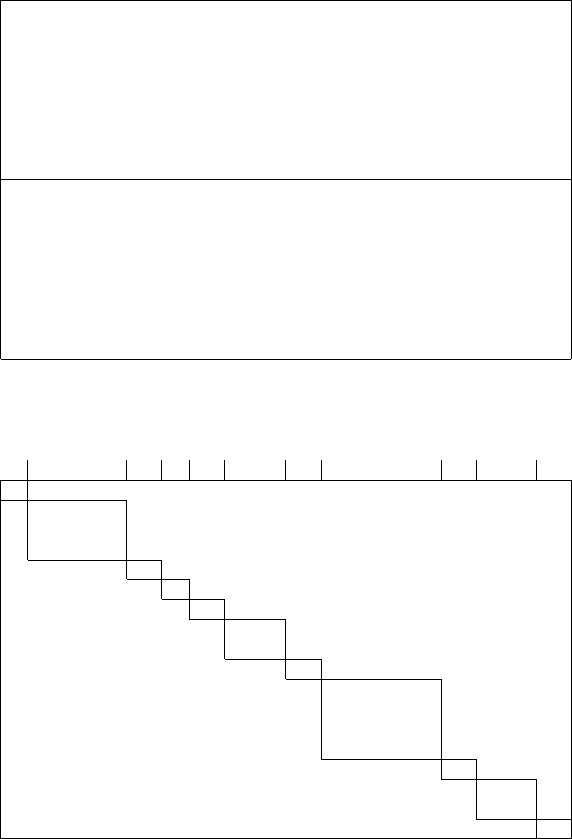
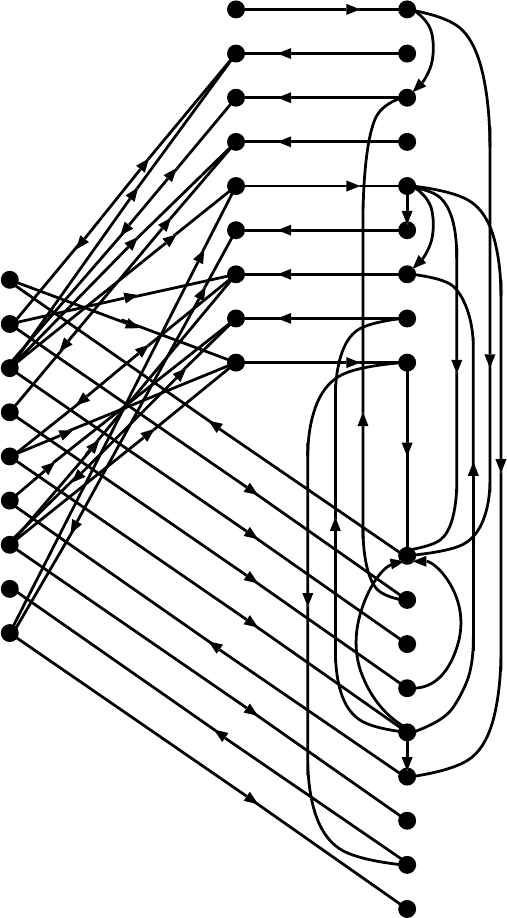
and the auxiliary network N =(G, γ)=(V, E, γ) is depicted in Fig. 6.10,
where x
T
i
= ϕ
T
(x
i
), x
Q
i
= ϕ
Q
(x
i
), etc. The associated length γ(a)isas
follows:
γ(a)=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
−1(a =(x
Q
6
,x
T
6
), (x
Q
7
,x
T
7
), (x
Q
8
,x
T
8
), (x
T
9
,x
Q
9
),
(w
T
2
,x
T
2
), (w
T
3
,x
T
3
), (w
T
9
,x
T
6
))
1(a =(w
Q
8
,w
T
8
), (x
T
2
,w
T
2
), (x
T
3
,w
T
3
), (x
T
6
,w
T
9
))
0 (otherwise).
The diagonal blocks in the CCF are determined from the strong compo-
nents of G. In particular, the diagonal blocks with indices in
¯
Ψ
1
= {2, 6}
correspond respectively to
ˆ
G
2
consisting of {w
T
2
,w
Q
2
,w
T
3
,x
T
2
,x
T
3
,x
Q
3
} and
ˆ
G
6
of {w
T
9
,x
T
5
,x
Q
5
,x
T
6
,x
Q
6
}. These two strong components are extracted in
Fig. 6.11, where the length γ(a) is attached in parentheses to each arc a.
Theorem 6.5.15 reveals that
ˆ
G
2
brings about nonzero fixed modes since
it contains a directed cycle of nonzero length. On the other hand,
ˆ
G
6
has
no directed cycle of nonzero length, introducing no nonzero fixed modes.
Accordingly,
ˆ
G
6
admits a potential function π such that π(x
T
6
)=−1,
π(w
T
9
)=π(x
T
5
)=π(x
Q
5
)=π(x
Q
6
) = 0. We also see by the equivalence of (i)
and (iii) in Theorem 6.5.12 that λ = 0 is a fixed mode, since T [I,J](0) = O,
K[I,J]=O, and rank Q(0)[I,J] ≤|I| + |J|−10 for I = {w
1
, ···,w
9
} and
J = {x
6
}. Furthermore, by Theorem 6.5.13, λ = 0 is simple (i.e., with mul-
tiplicity one). 2
Example 6.5.18. The present method successfully discriminates the exis-
tence of zero and nonzero fixed modes. Consider again the problem of Exam-
ple 6.5.8. It has a zero fixed mode and no nonzero fixed mode, while neither
graph-theoretic condition in Theorem 6.5.7 is satisfied. In line with Remark
6.5.16 we apply the present method to
6.5 Fixed Modes of Decentralized Systems 401
x
T
1
x
Q
1
x
T
2
x
Q
2
x
T
3
x
Q
3
x
T
4
x
Q
4
x
T
5
x
Q
5
x
T
6
x
Q
6
x
T
7
x
Q
7
x
T
8
x
Q
8
x
T
9
x
Q
9
w
T
1
w
Q
1
w
T
2
w
Q
2
w
T
3
w
Q
3
w
T
4
w
Q
4
w
T
5
w
Q
5
w
T
6
w
Q
6
w
T
7
w
Q
7
w
T
8
w
Q
8
w
T
9
w
Q
9
Fig. 6.10. Auxiliary network N in Example 6.5.17
