Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

362 6. Theory and Application of Mixed Polynomial Matrices

}≺{w

}≺{x

}≺{w

}

as a linear extension of the partial order in the CCF of

A(s; t). Then

A(s; t)=P



L(s) O



A(s; t)P

A(s; t)=P



U(s)L(s) O



A(s; t)P

with

L(s)=

⎛

⎜

⎝

−2s 1

−2s

⎞

⎟

⎠

,U(s)=

⎛

⎜

⎝

1 −3/s

⎞

⎟

⎠

and permutation matrices P

and P

. Note that L(s) is a unimodular poly-

nomial matrix in s over Q. The block-triangular matrix

A(s; t) is given by

A(s; t)=

∞

s 1 11

113s

−t

s τ

−t

10−2s 0

01−2s

−t

00 τ

0 −t

0 τ

00−t

+ τ

As claimed, the matrix

A is a polynomial matrix in s and it agrees with

in the diagonal blocks. Also notice the diﬀerence between the zero/nonzero

structures of

A and

A. In particular, we can exchange the positions of the

two blocks {w

} and {x

} in

A without destroying the block-triangular

structure if we accordingly exchange the corresponding rows, whereas these

two blocks must be arranged in this order in

A to put it in an explicit block-

triangular form. In other words, the square diagonal blocks are partially or-

dered as {w

}≺{w

}, {x

}≺{w

} with respect to the zero/nonzero

structure in

A, whereas they are totally ordered as {w

}≺{x

}≺{w

}

A. 2

Remark 6.3.11. It is natural to ask whether the Smith form of A(s)=

Q(s)+T (s) can be computed eﬃciently. This problem has been solved in

two special cases. If T (s)=O, then A(s) is simply a polynomial matrix over

K, for which Kannan [154] proposes a polynomial time algorithm. If Q(s)

satisﬁes the stronger condition (MP-Q2), which is trivially true in the other

extreme case of Q(s)=O, an eﬃcient (polynomial-time) matroid-theoretic

algorithm of §6.2 is available. 2

6.3 Smith Form of Mixed Polynomial Matrices 363

6.3.2 Proofs

A minor (subdeterminant) of A(s)=A(s, T ), is a polynomial in s and T

over K.Letd

∗

(s, T ) ∈ K[s, T ] denote the kth determinantal divisor of A,

i.e., the greatest common divisor of all minors of order k in A as polynomials

in (s, T )overK. Theorem 6.3.3 follows from the following lemma as well as

Lemma 6.3.2.

Lemma 6.3.12. d

∗

r−1

(s, T ) ∈ K[s], that is, no τ ∈T appears in d

∗

r−1

Proof. Since r =rankA, there exists a nonsingular submatrix A[I,J] with

|I| = |J| = r.Forτ ∈T let (i, j) denote the position at which τ appears in

A.Ifτ does not appear in δ = det A[I,J](= 0), then d

∗

r−1

is free from τ since

∗

r−1

divides δ.Ifτ does appear in δ, then i ∈ I and j ∈ J and furthermore



= det A[I \{i},J \{j}] = 0. Obviously, δ



does not contain τ and hence

∗

r−1

is free from τ since d

∗

r−1

divides δ



We now turn to the proof of Theorem 6.3.4. Firstly,

A(s; t)and

A(s; t)

share the same Smith form, since they are connected by a unimodular trans-

formation. Secondly, the Smith form Σ

(s)ofA(s) can be obtained from that

A(s; 1) by (6.56). The following lemma claims that

A(s; t)and

A(s;1)have

essentially identical Smith forms. We write

A(s; t, T )for

A(s; t) to explicitly

indicate its dependence on the coeﬃcients T in T (s).

Lemma 6.3.13. The Smith form of

A(s;1, T ), as a matrix over F [s],is

obtained from that of

A(s; t, T ), as a matrix over F (t)[s],bysettingt

···= t

=1. Conversely, the Smith form of

A(s; t, T ) is obtained from that

A(s;1, T ) by replacing τ ∈T with τ/t

if τ is contained in the ith row. 2

This allows us to concentrate on the Smith form of

A(s; t). Regard-

ing

A(s; t)=

A(s; t, T ) as a matrix over the ring K[s, t, T ], we denote by

r+m

(s; t)(∈ K[s, t, T ]) the (r + m)th determinantal divisor of

A(s; t). Then

(s)=α

r+m

(s;1), (6.61)

where α

∈ K(T ) ⊆ F is introduced for normalization to a monic polyno-

mial in F [s]. Since

A is block-triangularized with full-rank diagonal blocks

(cf. Theorem 4.4.19), a nonvanishing minor of

A of order r + m is expressed

det

A[R

,J] · det

A[I,C

∞

] ·



l=1

det

A[R

]

= det

A[R

,J] · det

A[I,C

∞

] ·



l=1

det

A[R

] (6.62)

for J ⊆ C

and I ⊆ R

∞

. Then Theorem 6.3.4 follows from (6.61) and (6.62)

and the lemma below, where gcd

K[s,t,T ]

{·} denotes the greatest common

divisor in the ring K[s, t, T ].

364 6. Theory and Application of Mixed Polynomial Matrices

Lemma 6.3.14.

gcd

K[s,t,T ]

{det

A[R

,J] ||J| = |R

|,J⊆ C

}∈K[s],

gcd

K[s,t,T ]

{det

A[I,C

∞

] ||I| = |C

∞

|,I⊆ R

∞

}∈K[s].

Proof. This follows from Theorem 4.5.8.

Notes. This section is based on Murota [213, 216].

6.4 Controllability of Dynamical Systems

Structural controllability of a control system is investigated using mixed poly-

nomial matrices. A necessary and suﬃcient condition for structural controlla-

bility is given in terms of the CCF of an associated LM-matrix, along with an

eﬃcient algorithm for testing it. As a special case, the structural controllabil-

ity of a descriptor system is expressed in terms of the Dulmage–Mendelsohn

decomposition of an associated bipartite graph.

6.4.1 Controllability

Controllability is one of the most fundamental characteristics for a control

system. A linear time-invariant dynamical system in the standard form

= Ax + Bu, (6.63)

where x = x(t) ∈ R

is the state-vector and u = u(t) ∈ R

is the input-

vector, is said to be controllable if any initial state x

= x(0) can be brought

to any prescribed ﬁnal state x

= x(t

) in a ﬁnite time t

by suitably chosen

input u(t)(0≤ t ≤ t

The following characterizations of controllability are well known (see

Kailath [152], Rosenbrock [284], Wolovich [342], Wonham [343]).

Theorem 6.4.1. The following ﬁve conditions are equivalent.

(i) The system (6.63) is controllable.

(ii) rank [B | AB | A

B |···|A

n−1

B]=n.

(iii) The n

× n(n + m − 1) matrix

D =

⎡

⎢

⎣

B −I

OAB−I

AB−I

⎤

⎥

⎦

(6.64)

is of rank n

(iv) rank [A − zI

| B]=n for any complex number z.

(v) The nth monic determinantal divisor of [A −sI

| B] is equal to 1. 2

6.4 Controllability of Dynamical Systems 365

The n × nm matrix [B | AB | A

B |···|A

n−1

B] in (ii) above is called

the controllability matrix, while [A −sI

| B]in(v)themodal controllability

matrix.

Controllability concept can be deﬁned for a system of descriptor form

= Ax + Bu (6.65)

in a number of diﬀerent ways (see, for example, Kodama–Ikeda [162], Pan-

dolﬁ [263], Hayakawa–Hosoe–Ito [108], Verghese–L´evy–Kailath [330], Yip–

Sincovec [349], Cobb [36]), where the matrix F is square (n × n) but not

necessarily nonsingular. We deﬁne the descriptor system (6.65) to be control-

lable if

rank [A − zF | B]=n for any complex number z. (6.66)

It should be obvious that this is equivalent to saying that the nth monic

determinantal divisor of [A − sF | B] is equal to 1.

The signiﬁcance of this deﬁnition of controllability can be understood with

reference to the canonical decomposition of a descriptor system explained in

Remark 5.1.9. It is easy to see from Theorem 6.4.1 that the descriptor system

(6.65) is controllable if and only if the subsystem (5.11) derived from it is

controllable in the ordinary sense. In other words, the present deﬁnition of

controllability means the controllability of the exponential modes, agreeing

with the notion of “R-controllability” of Yip–Sincovec [349].

For later references, we put together the relevant conditions:

(C1) det(A − sF ) =0,

(C2) rank [A | B]=n,

(C3) rank [A − zF | B]=n for any z ∈ C, z =0,

where it should be evident that (C2) and (C3) together are equivalent to the

controllability condition (6.66). The condition (C2) is for the controllability

of zero mode, whereas (C3) for nonzero modes. We often use the notation

D(s)=



A − sF



. (6.67)

6.4.2 Structural Controllability

The notion of “structural controllability” was ﬁrst introduced by Lin [173]

along with its graphical condition for single-input systems, followed by sub-

sequent extensions to multi-input systems by Shields–Pearson [295], Glover–

Silverman [94], Davison [45], Hosoe–Matsumoto [115], and Maeda [184]. It

also motivated many related works (e.g., Kobayashi–Yoshikawa [161], Maeda–

Yamada [185], Hosoe [113], Linnemann [174], Murota–Poljak [240], Reinschke

[279], Yamada–Foulds [345], Yamada–Luenberger [346, 347, 348]). This sec-

tion is devoted to a sketch of the graph-theoretic approach to structural

controllability with particular emphasis on the comparison of diﬀerent graph

366 6. Theory and Application of Mixed Polynomial Matrices

representations, signal-ﬂow graphs and dynamic graphs for systems in stan-

dard form, and bipartite graphs for systems in descriptor form. The reader

is referred to Murota [204, Chap. 3], Reinschke [279, Chap. 1], and

Siljak

[300, Chap. 1] for more details on the graph-theoretic approach to structural

controllability.

Let us ﬁrst consider the conventional case of the standard form (6.63).

Associated with a particular instance of the system (6.63) with the entries

of A and B being given concrete real numbers, we consider the structured

system, which is described by the same state-space equations as the original

system except that the nonvanishing entries of the coeﬃcient matrices A

and B are replaced by independent parameters (or indeterminates). Then

the original system is said to be structurally controllable if the associated

structured system is generically controllable with respect to those parameters,

i.e., if it is controllable (in the sense of Theorem 6.4.1) for those parameter

values which lie outside some proper algebraic variety in the parameter space.

It is easy to see that the structural controllability is equivalent to the

condition that the generic-rank of the controllability matrix is equal to n,

i.e.,

generic-rank [B | AB | A

B |···|A

n−1

B]=n (6.68)

with respect to those parameters. Note that the generic-rank of the controlla-

bility matrix of the structured system is equal to the rank of the controllabil-

ity matrix with parameter values ﬁxed to arbitrary transcendental numbers

which are algebraically independent over the rational number ﬁeld Q, since

each entry of the controllability matrix is a polynomial (with coeﬃcients from

Q) in those parameters. Note also that the condition (6.68) is not equivalent

term-rank [B | AB | A

B |···|A

n−1

B]=n.

The following is the fundamental result (Lin [173], Shields–Pearson [295],

Glover–Silverman [94], Maeda [184]) giving a graph-theoretic characterization

of the structural controllability in terms of the signal-ﬂow graph G =(V,E)

associated with (6.63). Recall from §2.2.1 that the vertex set V and the arc

set E are deﬁned by

V = X ∪ U, X = {x

, ···,x

},U= {u

, ···,u

E = {(x

) | A

=0}∪{(u

) | B

=0}.

By a stem we mean a directed path in G with its initial vertex belonging to

Theorem 6.4.2. A system in the standard form (6.63) is structurally con-

trollable if and only if the signal-ﬂow graph G satisﬁes both (a) and (b) below:

(a) There exists a set of mutually disjoint cycles and stems such that all the

vertices in X are covered,

6.4 Controllability of Dynamical Systems 367

(b) Any vertex x

(∈ X) is reachable by a directed path from some u

(∈ U ),

i.e., u

∗

−→ x

on G.

Proof. This theorem is derived later from a more general result in Remark

6.4.9. See also Shields–Pearson [295], Glover–Silverman [94], Davison [45],

Hosoe–Matsumoto [115], and Maeda [184], as well as Murota [204, Chap. 3],

Siljak [300, Chap. 1], and Linnemann [176].

A system is said to be reachable if it satisﬁes the condition (b) above,

namely, if any vertex x

(∈ X) is reachable by a directed path from some

(∈ U ) in the signal-ﬂow graph G.

The structural controllability can be characterized also in terms of the

dynamic graph, as is observed by Murota [204, Theorem 15.1]. Recall from

§2.2.1 (see also Example 2.2.4) that for a system (6.63) the dynamic graph

of time-span n is deﬁned to be G

=(X

∪ U

n−1

) with



t=0

= {x

| i =1, ···,n} (t =0, 1, ···,n),

n−1



t=0

= {u

| j =1, ···,m} (t =0, 1, ···,n−1),

n−1

= {(x

t+1

) | A

=0;t =0, 1, ···,n− 1}

∪{(u

t+1

) | B

=0;t =0, 1, ···,n−1}.

Theorem 6.4.3. A system in the standard form (6.63) is structurally con-

trollable if and only if there exists in the dynamic graph G

of time-span n a

Menger-type vertex-disjoint linking of size n from U

n−1

to X

Proof. This follows from Theorem 6.4.4 below.

The generic dimension of the controllable subspace means the generic rank

of the controllability matrix, i.e., rank [B | AB | ··· | A

n−1

B] when the

nonzero entries of A and B are algebraically independent parameters. A sys-

tem is structurally controllable if and only if the generic dimension of the

controllable subspace is equal to n.

The following result of Poljak [271] is an extension of Theorem 6.4.3 above.

Theorem 6.4.4. Forareachablesystem(6.63), the generic dimension of the

controllable subspace is equal to the maximum size of a Menger-type vertex-

disjoint linking from U

n−1

to X

in the dynamic graph G

of time-span n.

Proof. The proof is based on the max-ﬂow min-cut theorem (Theorem 2.2.30)

and Theorem 6.4.5 below. See Poljak [271] for the detail.

The following theorem, due to Hosoe [113], is a fundamental result on the

generic dimension of the controllable subspace. For X



⊆ X = {x

, ···,x

}

we use the notation [A[X



] | B[X



,U]] to mean the |X



|×(|X



| + m)

368 6. Theory and Application of Mixed Polynomial Matrices

matrix formed with the submatrices A[X



]andB[X



,U], where U =

, ···,u

Theorem 6.4.5. For a reachable system (6.63), the generic dimension of

the controllable subspace is equal to

max{|X



||term-rank ([A[X



] | B[X



,U]]) = |X



|,X



⊆ X}.

Remark 6.4.6. Under the reachability assumption, Theorem 6.4.4 implies

term-rank

D = generic-rank

for the matrix

D in (6.64), where the generic-rank is deﬁned with respect

to the nonzero entries of A and B. Note that generic-rank

D = n(n − 1) +

generic-rank [B | AB |···|A

n−1

B] and that term-rank

D equals to n(n −1)

plus the maximum size of a Menger-type vertex-disjoint linking from U

n−1

in G

. The former can be shown by row elimination on

D and the latter

by the linkage lemma (cf. Murota [204, Prop. 7.1], Welsh [333, Chap. 13, §1]).

In the remainder of this section we consider structural controllability for

descriptor systems, following Murota [199]. As has been discussed in §1.2.2,

the descriptor form (6.65) is a more elementary description than the stan-

dard form (6.63), and hence will be more suitable for structural analysis. We

deﬁne a descriptor system (6.65) to be structurally solvable if the condition

(C1) in §6.4.1 is satisﬁed under the assumption that the nonvanishing entries

of the coeﬃcient matrices F , A,andB are algebraically independent over

Q. A descriptor system (6.65) is said to be structurally controllable if, in

addition, the conditions (C2) and (C3) in §6.4.1 are satisﬁed under the same

assumption.

We shall derive a necessary and suﬃcient graph-theoretic condition for the

structural controllability. As has been discussed in §2.2.1, the natural graph

representation of a descriptor system is a bipartite graph, and accordingly, it

will be reasonable to aim at establishing a graph-theoretic condition on the

bipartite graph for the structural controllability.

Let G =(V

−

; E) be the bipartite graph associated with the descrip-

tor system (6.65). Namely, V

= X ∪ U = {x

, ···,x

}∪{u

, ···,u

−

= {e

, ···,e

},andE = E

∪ E

with E

= {(x

) | A

=0},

= {(x

) | F

=0},andE

= {(u

) | B

=0}. No parallel arcs are

introduced even if E

∩E

= ∅. We call an arc an s-arc if it belongs to E

The ﬁrst two conditions (C1) and (C2) are easy to handle. Let G

A−sF

and G

[A|B]

denote the bipartite graphs associated with A − sF and [A |

B], respectively. Namely, G

A−sF

=(X, V

−

; E

∪ E

)andG

[A|B]

=(X ∪

U, V

−

; E

∪ E

). Then, by Proposition 2.2.25, we have

(C1) ⇐⇒ term-rank (A − sF )=n ⇐⇒ ν(G

A−sF

)=n, (6.69)

(C2) ⇐⇒ term-rank [A | B]=n ⇐⇒ ν(G

[A|B]

)=n, (6.70)

6.4 Controllability of Dynamical Systems 369

where ν( ·) denotes the size of a maximum matching in a bipartite graph.

For the third condition (C3) we consider the DM-decomposition of G.Let

=(V

−

; E

)(k =0, 1, ···,b,∞) be the DM-components of G =

−

; E). In this notation, k =0andk = ∞ designate the horizontal tail

and the vertical tail, respectively, though the vertical tail does not exist (is

empty) under the condition (C1) or (C2).

A necessary and suﬃcient graph-theoretic condition for the structural

controllability of a descriptor system is given as follows (Murota [199]).

Theorem 6.4.7. A descriptor system (6.65) is structurally solvable if and

only if

(B1) ν(G

A−sF

)=n.

It is structurally controllable if and only if the following two conditions (B2)

and (B3) hold in addition to (B1):

(B2) ν(G

[A|B]

)=n,

(B3) None of the consistent DM-components G

(k =1, ···,b) of the bipar-

tite graph G contain s-arcs.

Proof. This follows from (6.69), (6.70), and Theorem 6.3.8 as well as Theorem

6.4.1(v). See Murota [204, §14.2] for an alternative proof.

In the particular case with nonsingular F , Theorem 6.4.7 reduces to the

following, which makes no reference to the DM-decomposition.

Corollary 6.4.8. A descriptor system (6.65) with term-rank F = n is struc-

turally controllable if and only if the following two conditions (B2) and (B4)

hold:

(B2) ν(G

[A|B]

)=n,

(B4) ν(G \{x

})=n for any x

∈ X.

Proof. Since term-rank F = n, the condition (B3) is satisﬁed if and only if

the whole graph G is the horizontal tail. The latter condition is equivalent

to (B4) by Corollary 2.2.23(2).

Remark 6.4.9. Theorem 6.4.2 can be derived from Corollary 6.4.8. First ob-

serve that the system in the standard form (6.63) is structurally controllable

if and only if so is the descriptor system (6.65) with the same A and B, and a

nonsingular diagonal F. The condition (a) in Theorem 6.4.2 is easily seen to

be equivalent to (B2). According to the algorithm for the DM-decomposition

in §2.2.3, the condition (b) in Theorem 6.4.2 is equivalent to saying that the

whole graph G is the horizontal tail, which is equivalent to (B4) by Corollary

2.2.23(2). 2

370 6. Theory and Application of Mixed Polynomial Matrices

The conditions given in Theorem 6.4.7 can be checked eﬃciently with

O((m+n)

5/2

) graph manipulations as follows. (B1) and (B2) may be checked

by ﬁnding maximum matchings in G

A−sF

and G

[A|B]

, respectively. Suppose

(B1) is satisﬁed and there exists in G

A−sF

a perfect matching, say M.It

is also a maximum matching in G.LetG

=(V

∪ V

−

,E ∪ M

◦

)bethe

auxiliary graph associated with the matching M in G, where M

◦

is the set

of reorientations of the arcs in M, and deﬁne G



to be the subgraph of G

which is obtained from G

by deleting all the vertices reachable from U.

Then (B3) is equivalent to the condition that none of the strong components

of G



contain s-arcs.

Remark 6.4.10. Graph-theoretic conditions for the structural controllabil-

ity of a descriptor system were ﬁrst given, almost simultaneously, by Aoki–

Hosoe–Hayakawa [7] and Matsumoto–Ikeda [187] with diﬀerent expressions.

However, both of these graph-theoretic conditions lack in the natural in-

variance, being expressed in terms of noninvariant graph representations as

follows. Aoki–Hosoe–Hayakawa [7] uses a graph

G =(V, E)thathasvertex

set V = X ∪ U and the arc set

E = {(x

) | (A − sF )

=0}∪{(u

) | B

=0}.

The graph

G thus deﬁned is not unique in that

G depends on the casual choice

of ordering of the equations. In particular, the subgraph of

G on X does not

reﬂect the fact that A − sF is subject not to similarity transformations,

but to equivalence transformations. On the other hand, Matsumoto–Ikeda

[187] employs a graph representation which can only be determined after a

maximum matching on the bipartite graph associated with A −sF is found.

This representation is not unique, either, since it depends on the choice of

the maximum matching.

Though the conclusions derived from the criteria of Aoki–Hosoe–Hayakawa

[7] and Matsumoto–Ikeda [187] are known to be unaﬀected by the nonunique-

ness of the graph representations, it would be preferable to express the con-

trollability condition in such a way that the underlying invariance may be

represented explicitly. The conditions (B1)–(B3) in Theorem 6.4.7 are invari-

ant in this respect, since the DM-decomposition of the bipartite graph G

remains the same (isomorphic) under the changes of ordering of equations. 2

Example 6.4.11. The structural controllability criterion in Theorem 6.4.7

is illustrated for a descriptor system (6.65) with

F =

⎛

⎝

000

⎞

⎠

,A=

⎛

⎝

00a

⎞

⎠

,B=

⎛

⎝

⎞

⎠

which is taken from Matsumoto–Ikeda [187]. We assume that the set of

parameters {f

; a

; b} is algebraically independent over

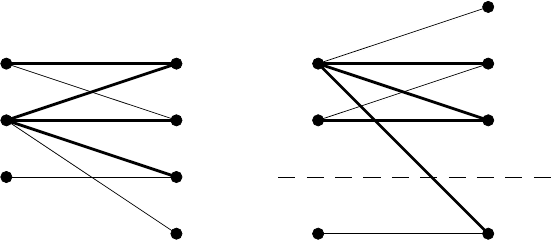
6.4 Controllability of Dynamical Systems 371

Q. The bipartite graph G is depicted in Fig. 6.5 together with its DM-

decomposition, which consists of the horizontal tail G

=(V

−

; E

) with

= {x

,u} and V

−

= {e

}, and the only one consistent component

=(V

−

; E

) with V

= {x

}, V

−

= {e

},andE

= {a

}.Nos-arc is

contained in G

, in agreement with the condition (B3) of Theorem 6.4.7. The

other two conditions, (B1) and (B2), are easily seen to be met. Thus this sys-

tem has been shown to be structurally controllable. It should be noted that

the s-arcs contained in G

do not aﬀect the controllability. 2

−

Graph G

−

DM-decomposition

Fig. 6.5. Bipartite graph G of Example 6.4.11 and its DM-decomposition (bold

line: s-arc)

Example 6.4.12. Modify the system of Example 6.4.11 by ﬁxing a

= 0, fol-

lowing Matsumoto–Ikeda [187]. That is, we assume {f

; a

; b}

is the set of algebraically independent parameters. The two conditions (B1)

and (B2) are still satisﬁed, whereas (B3) is not, as demonstrated in Fig. 6.6.

The DM-decomposition of the modiﬁed bipartite graph yields a horizontal

tail G

with V

= {x

,u} and V

−

= {e

}, and two consistent compo-

nents G

with V

= {x

} and V

−

= {e

},andG

with V

= {x

} and

−

= {e

}. The component G

contains an s-arc. In fact, it is easy to verify

that rank D(z)=2< 3forz = a

. 2

Example 6.4.13. Consider the descriptor system (6.65) given by

F =

⎛

⎜

⎝

0 f

0000

⎞

⎟

⎠

,A=

⎛

⎜

⎝

000a

0 a

⎞

⎟

⎠

,B=

⎛

⎜

⎝

⎞

⎟

⎠