Murota K. Matrices and Matroids for Systems Analysis
Подождите немного. Документ загружается.


352 6. Theory and Application of Mixed Polynomial Matrices
M := M −{a ∈ M | a ∈ L ∩ M
◦
} +(L ∩ (E
T
∪ E
Q
)) ; k := k +1;
p[v]:=p[v]+Δp(v)(v ∈
˜
V ); [cf. (6.49)]
For all (i
Q
,j
Q
) ∈ L ∩ E
+
(in the order from S
+
to S
−
along L)dothe
following:
{Find h such that i = base[h];
B := B −i
Q
+ j
Q
; δ
Q
:= δ
Q
+ deg
s
P [h, j];
base[h]:=j; w := 1/P [h, j];
P [h, l]:=w × P [h, l](l ∈ C); S[h, l]:=w × S[h, l](l ∈ R
Q
);
P [m, l]:=P [m, l] − P [m, j] × P [h, l](m ∈ R
Q
\{h},l ∈ C \{j});
S[m, l]:=S[m, l] − P [m, j] × S[h, l](m ∈ R
Q
\{h},l ∈ R
Q
);
P [m, j]:=0 (m ∈ R
Q
\{h}) };
Go to Step 3. 2
Step 2 for finding a maximum-weight base B ∈B
Q
is justified by the
greedy algorithm for a valuated bimatroid given in §5.2.5 (see also Example
5.2.15).
For the updates of P in Steps 2 and 4, the algorithm assumes the avail-
ability of arithmetic operations on rational functions in a single variable s
over the subfield K. It is emphasized that no arithmetic operations are done
on the T -part, so that no rational function operations involving coefficients
in T (which are independent symbols) are needed.
The updates of P are the standard pivoting operations on rational func-
tions in s over K, the total number of which is bounded by O(|R|
2
|C|k
max
).
Note that pivoting operations are required for each arc (i
Q
,j
Q
) ∈ L ∩ E
+
(see Step 4). The sparsity of P should be taken into account in actual imple-
mentations of the algorithm.
The matrix S(s) gives the inverse of Q[R
Q
,B], which is often useful (see,
e.g., the proof of Theorem 6.2.12). When S(s) is not needed, it may simply
be eliminated from the computation without any side effect.
The shortest path in Step 4 can be found in time linear in the size of the
graph
˜
G, which is O((|R|+|C|)
2
), by means of the standard graph algorithms;
see, e.g., Aho–Hopcroft–Ullman [1, 2].
Remark 6.2.17. The above algorithm can be used to compute δ
k
(A)fora
mixed polynomial matrix A(s) by considering the associated LM-mixed poly-
nomial matrix on the basis of Lemma 6.2.6. This is what is called “Algorithm
D” in §1.3.2. 2
Example 6.2.18. The algorithm above is illustrated here for the 4 ×5LM-
polynomial matrix A(s) of (6.25):
A(s)=
x
1
x
2
x
3
x
4
x
5
s
3
0 s
3
+1 s
2
1
0 s
2
s
2
s 0
f
1
−t
1
s
3
00α
1
α
2
s
f
2
0 −t
2
s
2
α
3
00
.
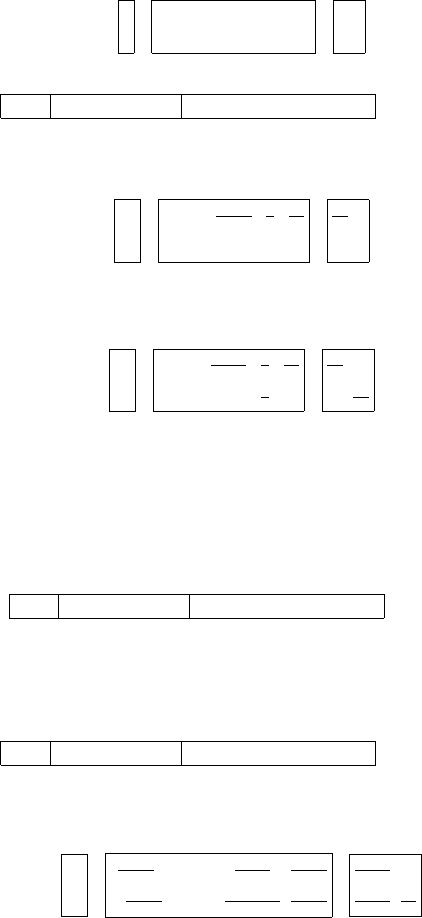
6.2 Degree of Determinant of Mixed Polynomial Matrices 353
We work with a 2 ×5 matrix P(s), a 2 ×2 matrix S(s), a vector base of size
2, and another vector p of size 12.
The flow of computation is traced below.
Step 1: M := ∅; B := ∅; δ
Q
:= 0;
(base, P, S):=
r
1
0
r
2
0
,
x
1
x
2
x
3
x
4
x
5
s
3
0 s
3
+1 s
2
1
0 s
2
s
2
s 0
,
10
01
;
p :=
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
3300000 00000
.
Step 2: (h, j):=(r
1
,x
1
); B := {x
1Q
}, δ
Q
:= 3; M := {(x
1Q
,x
1
)};
(base, P, S):=
r
1
x
1
r
2
0
,
x
1
x
2
x
3
x
4
x
5
10
s
3
+1
s
3
1
s
1
s
3
0 s
2
s
2
s 0
,
1
s
3
0
01
;
(h, j):=(r
2
,x
2
); B := {x
1Q
,x
2Q
}, δ
Q
:= 5; M := {(x
1Q
,x
1
), (x
2Q
,x
2
)};
(base, P, S):=
r
1
x
1
r
2
x
2
,
x
1
x
2
x
3
x
4
x
5
10
s
3
+1
s
3
1
s
1
s
3
01 1
1
s
0
,
1
s
3
0
0
1
s
2
;
k := 0.
Step 3: δ
LM
0
(A):=5;S
+
:= {f
1
,f
2
}; S
−
:= {x
3
,x
4
,x
5
};
M
◦
:= {(x
1
,x
1Q
), (x
2
,x
2Q
)};
E
+
:= {(x
1Q
,x
3Q
), (x
1Q
,x
4Q
), (x
1Q
,x
5Q
), (x
2Q
,x
3Q
), (x
2Q
,x
4Q
)};
γ and γ
p
are given in
˜
G
(0)
of Fig. 6.2. [See
˜
G
(0)
in Fig. 6.2]
Step 4:
Δp :=
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
0001012 01013
;
There exists a path from S
+
to S
−
;
L := {(f
1
,x
1
), (x
1
,x
1Q
), (x
1Q
,x
3Q
), (x
3Q
,x
3
)};
M := {(f
1
,x
1
), (x
2Q
,x
2
), (x
3Q
,x
3
)}; k := 1;
p :=
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
3301012 01013
;
(i
Q
,j
Q
):=(x
1Q
,x
3Q
) ∈ L ∩ E
+
; h := r
1
; B := {x
3Q
,x
2Q
}, δ
Q
:= 5;
(base, P, S):=
r
1
x
3
r
2
x
2
,
x
1
x
2
x
3
x
4
x
5
s
3
s
3
+1
01
s
2
s
3
+1
1
s
3
+1
−
s
3
s
3
+1
10
1
s(s
3
+1)
−1
s
3
+1
,
1
s
3
+1
0
−1
s
3
+1
1
s
2
.
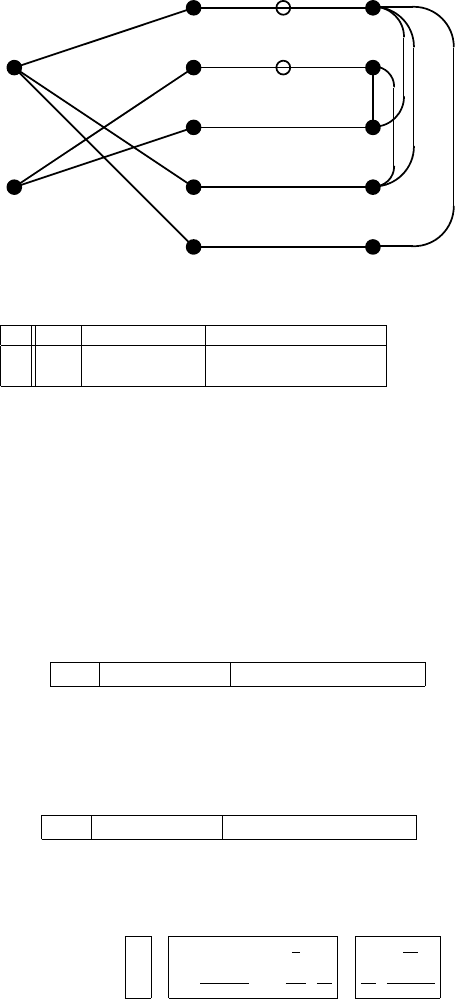
354 6. Theory and Application of Mixed Polynomial Matrices
R
T
CC
Q
E
T
E
Q
E
+
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
+
+
−
−
−
1
γ/γ
p
= −3/0
s
0/3
R
−1/2
3
−2/1
1
0/3
γ/γ
p
=0/0
0/0
0/0
0/0
0/0
-
-
?
0/0
?
1/1
?0/0
?1/1
?
3/3
v f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
p 3300000 00000
Δp 0001012 01013
Fig. 6.2. Graph
˜
G
(0)
(:arcinM, B = {x
1Q
,x
2Q
}, S
+
= {f
1
,f
2
}, S
−
=
{x
3
,x
4
,x
5
})
Step 3: δ
LM
1
(A):=5+3=8;S
+
:= {f
2
}; S
−
:= {x
4
,x
5
};
M
◦
:= {(x
1
,f
1
), (x
2
,x
2Q
), (x
3
,x
3Q
)};
E
+
:= {(x
2Q
,x
1Q
), (x
2Q
,x
4Q
), (x
2Q
,x
5Q
), (x
3Q
,x
1Q
),
(x
3Q
,x
4Q
), (x
3Q
,x
5Q
)};
γ and γ
p
are given in
˜
G
(1)
of Fig. 6.3. [See
˜
G
(1)
in Fig. 6.3]
Step 4:
Δp :=
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
1010331 10331
;
There exists a path from S
+
to S
−
;
L := {(f
2
,x
2
), (x
2
,x
2Q
), (x
2Q
,x
1Q
), (x
1Q
,x
1
), (x
1
,f
1
), (f
1
,x
5
)};
M := {(f
1
,x
5
), (f
2
,x
2
), (x
1Q
,x
1
), (x
3Q
,x
3
)}; k := 2;
p :=
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
4311343 11344
;
(i
Q
,j
Q
):=(x
2Q
,x
1Q
) ∈ L ∩ E
+
; h := r
2
; B := {x
3Q
,x
1Q
}, δ
Q
:= 5;
(base, P, S):=
r
1
x
3
r
2
x
1
,
x
1
x
2
x
3
x
4
x
5
011
1
s
0
1
−s
3
−1
s
3
0
−1
s
4
1
s
3
,
0
1
s
2
1
s
3
−s
3
−1
s
5
.
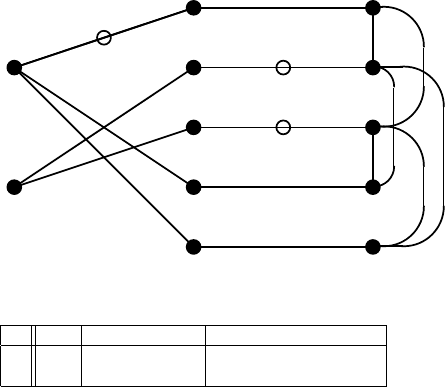
6.3 Smith Form of Mixed Polynomial Matrices 355
R
T
CC
Q
E
T
E
Q
E
+
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
+ −
−
1
γ/γ
p
= ±3/0
s
0/2
R
−1/0
3
−2/0
1
0/3
γ/γ
p
=0/0
0/0
0/0
0/0
0/1
)
-
-
60/1
?
4/4
6
0/0
?3/0
?3/1
?
1/0
v f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
p 3301012 01013
Δp 1010331 10331
Fig. 6.3. Graph
˜
G
(1)
(:arcinM, B = {x
2Q
,x
3Q
}, S
+
= {f
2
}, S
−
= {x
4
,x
5
})
Step 3: δ
LM
2
(A):=5+3=8;S
+
:= ∅; S
−
:= {x
4
};
M
◦
:= {(x
5
,f
1
), (x
2
,f
2
), (x
1
,x
1Q
), (x
3
,x
3Q
)};
E
+
:= {(x
1Q
,x
2Q
), (x
1Q
,x
4Q
), (x
1Q
,x
5Q
), (x
3Q
,x
2Q
), (x
3Q
,x
4Q
)};
γ and γ
p
are given in
˜
G
(2)
of Fig. 6.4. [See
˜
G
(2)
in Fig. 6.4]
Step 4: There exists no path from S
+
(= ∅)toS
−
;
Stop with k
max
:= 2.
2
Notes. This section is based mostly on Murota [233]. In particular, The-
orems 6.2.8, 6.2.11, 6.2.14, and 6.2.15 are found in Murota [233], whereas
Theorem 6.2.4 is given in Murota [200]. The problem of computing the de-
gree of determinant will be considered again in §7.1.
6.3 Smith Form of Mixed Polynomial Matrices
The Smith normal form of a mixed polynomial matrix A(s)=Q(s)+T (s)
is investigated. It is shown that all the invariant factors except for the last
are polynomials in s free from the coefficients in T (s), and the last invariant
factor can be expressed in terms of the CCF of an associated LM-matrix.
6.3.1 Expression of Invariant Factors
Let A(s)=Q(s)+T (s)beanm ×n mixed polynomial matrix of rank r with
respect to (K, F ) satisfying, by definition, (MP-Q1) and (MP-T) in §6.1.1.
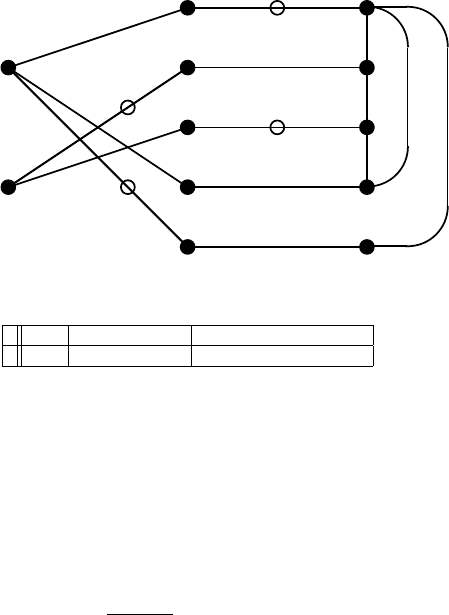
356 6. Theory and Application of Mixed Polynomial Matrices
R
T
CC
Q
E
T
E
Q
E
+
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
−
1
γ/γ
p
= −3/0
s
0/0
R
±1/0
3
±2/0
1
0/0
γ/γ
p
=0/0
0/0
0/0
0/0
0/1
-
+
-
I
?
0/0
?4/1
?
3/0
60/2
?
1/0
v f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
p 4311343 11344
Fig. 6.4. Graph
˜
G
(2)
(:arcinM, B = {x
1Q
,x
3Q
}, S
+
= ∅, S
−
= {x
4
})
Regarding A(s) as a polynomial matrix in s over F , we define (cf. §5.1.1) the
kth determinantal divisor d
k
(s) ∈ F [s]by
d
k
(s)=gcd
F [s]
{det A[I,J] ||I| = |J| = k} (k =1, ···,r) (6.51)
and the kth invariant factor e
k
(s) ∈ F [s]by
e
k
(s)=
d
k
(s)
d
k−1
(s)
(k =1, ···,r), (6.52)
where d
k
(s)ande
k
(s) are chosen to be monic in F [s]fork =1, ···,r. Then
the Smith form of A(s) is given (cf. Theorem 5.1.1) by
Σ
A
(s) = diag (e
1
(s), ···,e
r
(s), 0, ···, 0).
Note that the coefficients of d
k
(s)ande
k
(s) are, in general, rational functions
in T over K, where T (⊆ F ) denotes the set of the coefficients in the entries
of T (s).
Example 6.3.1. Consider a 2 × 2 mixed polynomial matrix A(s)=Q(s)+
T (s) with respect to (K, F )=(Q, Q(τ
1
,τ
2
,τ
3
)) given by
A(s)=
s + τ
1
s + τ
3
0 τ
2
s +1
,Q(s)=
ss
01
,T(s)=
τ
1
τ
3
0 τ
2
s
.
The Smith form of A(s) is given by Σ
A
(s) = diag [1, (s+τ
1
)(s+1/τ
2
)], which
is true under the condition of algebraic independence of T = {τ
1
,τ
2
,τ
3
}.

6.3 Smith Form of Mixed Polynomial Matrices 357
This expression, however, is no longer valid if specific numerical values are
given to the parameters in T . Namely, it can be verified easily that Σ
A
(s)=
diag [s + τ
1
,s+ τ
1
]ifτ
1
=1/τ
2
= τ
3
, and otherwise the first expression is
valid. It is emphasized that the theorems of this section deal with the generic
situation where no algebraic relation exists among the parameters in T . 2
Before entering into the Smith form it is in order to point out a remarkable
implication of the stronger condition on Q(s):
(MP-Q2) Every nonvanishing subdeterminant of Q(s) is a monomial
over K, i.e., of the form αs
p
with α ∈ K and an integer p,
introduced for physical-dimensional consistency. If A(s)=Q(s)+T (s)is
nonsingular, its determinant is a nonvanishing polynomial in (s, T )overK.
The following lemma claims that det A(s) contains no (nonmonomial) poly-
nomial in s free from T as an irreducible factor in K[s, T ]. This fact affords
a rich structure to the class of mixed polynomial matrices with the condition
(MP-Q2) (see Remark 6.2.10 for another implication of (MP-Q2)).
Lemma 6.3.2. For a nonsingular mixed polynomial matrix A(s)=Q(s)+
T (s) satisfying the stronger condition (MP-Q2), the decomposition of det A(s)
into irreducible factors in K[s, T ] is expressed as
det A(s)=αs
p
·
k
ψ
k
(s, T ),
where α ∈ K \{0}, p is a nonnegative integer, and ψ
k
(s, T ) ∈ K[s, T ] \K[s]
and ψ
k
(s, T ) is irreducible in K[s, T ] for each k.Hence,det A(z)=0for z
algebraic over K(T ) implies either z =0or z is transcendental over K.
Proof. By (6.4) we have
A(s) = diag [s
r
1
, ···,s
r
n
] · (Q(1) +
˜
T (s)) · diag [s
−c
1
, ···,s
−c
n
],
where
˜
T (s) = diag [s
−r
1
, ···,s
−r
n
] ·T (s) ·diag [s
c
1
, ···,s
c
n
]. For any nonzero
number, say z, that is algebraic over K, Q(1) +
˜
T (z) is a mixed matrix
with respect to (K, F (z)). Applications of Theorem 4.2.8 to Q(1) +
˜
T (s)and
Q(1) +
˜
T (z) show that the nonsingularity of A(s) implies that of A(z). This
means that det A(s) has no factor in K[s] except for a monomial in s.
The properties of the Smith form of A(s) are stated in Theorems 6.3.3 and
6.3.4 below. The former refers to e
k
(s)fork =1, ···,r−1, whereas the latter
to e
r
(s). Recall the notation ord
s
(·) for the lowest degree of a nonvanishing
term of a polynomial (cf. §2.1.1).
Theorem 6.3.3. Let A(s)=Q(s)+T (s) be a mixed polynomial matrix of
rank r with respect to (K, F ).Fork =1, ···,r− 1, the kth monic determi-
nantal divisor d
k
(s) and the kth monic invariant factor e
k
(s) of A(s) contain

358 6. Theory and Application of Mixed Polynomial Matrices
no elements of T , that is, d
k
(s) ∈ K[s] and e
k
(s) ∈ K[s]. Moreover, if Q(s)
satisfies the stronger condition (MP-Q2), then they are monomials:
d
k
(s)=s
p
k
,e
k
(s)=s
p
k
−p
k−1
(k =1, ···,r−1) (6.53)
with exponents given by
p
k
= min{ord
s
det A[I,J] ||I| = |J| = k} (k =1, ···,r−1), (6.54)
where p
0
=0by convention.
Proof. The proof is given in §6.3.2.
To determine the last invariant factor e
r
(s) we associate with A(s)an
augmented (2m) × (m + n) matrix
˜
A(s)=
˜
A(s; t)=
I
m
Q(s)
−diag (t
1
, ···,t
m
) T(s)
=
˜
Q(s)
˜
T (s; t)
, (6.55)
where t
1
, ···,t
m
are new indeterminates, t =(t
1
, ···,t
m
), and
˜
Q(s)=[I
m
| Q(s)],
˜
T (s; t)=[−diag (t
1
, ···,t
m
) | T (s)].
Since
I
m
O
I
m
I
m
I
m
Q(s)
−I
m
T (s)
I
m
−Q(s)
OI
n
=
I
m
O
OA(s)
,
the Smith form of
˜
A(s;1) =
˜
A(s; t)
8
8
8
t
1
=···=t
m
=1
is given as
I
m
O
OΣ
A
(s)
(6.56)
in terms of the Smith form Σ
A
(s)ofA(s). In particular, the last invariant
factor of
˜
A(s; 1) is equal to e
r
(s).
The augmented matrix
˜
A(s; t) in (6.55) is an LM-matrix with respect
to (K(s), F (s, t)). It can also be viewed as an LM-matrix with respect to
(K[s], F (s, t)) for the integral domain D = K[s] in the sense of §4.4.7, i.e.,
˜
A(s; t) ∈ LM(K[s], F (s, t)), since
˜
Q(s) is a polynomial matrix over K.The
CCF of such an LM-matrix has been considered in Theorem 4.4.19.
Let
¯
A =
¯
A(s; t) be the CCF of
˜
A(s; t) in Theorem 4.4.19 and denote by
{
¯
A
l
(s; t) | l =0, 1, ···,b,∞} the family of the LM-irreducible diagonal blocks
of
¯
A(s; t), where
¯
A
0
=
¯
A
0
(s; t)and
¯
A
∞
=
¯
A
∞
(s; t) are the horizontal and the
vertical tail, and
¯
A
l
=
¯
A
l
(s; t)(l =1, ···,b) are the square LM-irreducible
blocks; we put R
l
=Row(
¯
A
l
)andC
l
= Col(
¯
A
l
)forl =0, 1, ···,b,∞. Recall
from Theorem 4.4.19 that there exists
ˆ
A(s; t) obtained from
˜
A(s; t) through
a unimodular transformation over K[s] such that
ˆ
A[R
l
,C
j
]=
¯
A[R
l
,C
j
]=
O for l>jand
ˆ
A[R
l
,C
l
]=
¯
A[R
l
,C
l
]forl =0, 1, ···,b,∞. In particular,
the diagonal block
¯
A[R
l
,C
l
] consists of polynomials in (s, t, T )overK for

6.3 Smith Form of Mixed Polynomial Matrices 359
l =0, 1, ···,b,∞. We denote by
¯
d
0
r
(s)and
¯
d
∞
r
(s) the monic determinantal
divisors in F (t)[s] of the largest order of
¯
A
0
(s; t)and
¯
A
∞
(s; t), respectively.
The following theorem states that e
r
(s) is characterized by the diagonal
blocks of
¯
A(s; t).
Theorem 6.3.4. Let A(s)=Q(s)+T (s) be a mixed polynomial matrix of
rank r with respect to (K, F ) and {
¯
A
l
(s; t) | l =0, 1, ···,b,∞} be as above.
The rth monic determinantal divisor d
r
(s) and the rth monic invariant factor
e
r
(s) of A(s) can be expressed as
d
r
(s)=α
r
·d
r
(s)·
b
l=1
det
¯
A
l
(s;1),e
r
(s)=α
r
·e
r
(s)·
b
l=1
det
¯
A
l
(s;1), (6.57)
where α
r
∈ F , d
r
(s)=
¯
d
0
r
(s) ·
¯
d
∞
r
(s) ∈ K[s],ande
r
(s) ∈ K[s].Moreover,if
Q(s) satisfies the stronger condition (MP-Q2), it holds that
¯
d
0
r
(s)=s
¯p
0
r
,
¯
d
∞
r
(s)=s
¯p
∞
r
,e
r
(s)=s
¯p
0
r
+¯p
∞
r
−p
r−1
, (6.58)
where
¯p
0
r
= min{ord
s
det
¯
A
0
(s; t)[R
0
,J] ||J| = |R
0
|}, (6.59)
¯p
∞
r
= min{ord
s
det
¯
A
∞
(s; t)[I,C
∞
] ||I| = |C
∞
|}, (6.60)
and p
r−1
is given by (6.54).
Proof. The proof is given in §6.3.2.
As a corollary to this theorem we can identify those parameters in T
which affect the Smith form of A(s).
Theorem 6.3.5. The rth monic invariant factor of A(s) depends on τ ∈T
if and only if τ is contained in some square LM-irreducible block
¯
A
l
(s; t) of
the CCF of
˜
A(s; t) such that det
¯
A
l
(s; t) is not a monomial in s over F .
Proof. Recall the expression of e
r
(s) in Theorem 6.3.4. All the parameters of T
contained in
¯
A
l
(s; 1) with 1 ≤ l ≤ b appear in det
¯
A
l
(s; 1) by Theorem 4.5.4.
They remain after the normalization by α
r
∈ F if and only if det
¯
A
l
(s;1) is
not a monomial in s over F .
Remark 6.3.6. The monomiality of det
¯
A
l
(s; 1) in Theorem 6.3.5 can be
checked efficiently by computing deg
s
det
¯
A
l
(s; 1) and ord
s
det
¯
A
l
(s;1) by
the algorithm of §6.2, since det
¯
A
l
(s; 1) is monomial in s if and only if
deg
s
det
¯
A
l
(s;1) = ord
s
det
¯
A
l
(s; 1). See §6.4.4 for a concrete procedure for
this idea with an additional improvement. 2
Remark 6.3.7. In case A(s) is an LM-matrix, there is no need to introduce
the augmented LM-matrix
˜
A(s; t). The claims in Theorems 6.3.4 and 6.3.5
remain valid when we redefine
¯
A to be the CCF of A(s) ∈ LM(K[s], F (s))
such as in Theorem 4.4.19. 2

360 6. Theory and Application of Mixed Polynomial Matrices
Let us specialize Theorems 6.3.3 and 6.3.4 to a generic polynomial ma-
trix A(s) (of which all the nonzero coefficients are algebraically indepen-
dent). Such A(s) is a mixed polynomial matrix with Q(s)=O, satisfying the
stronger assumption (MP-Q2) trivially.
Theorem 6.3.8. Let A(s) be a generic polynomial matrix of rank r,and
{
¯
A
l
(s) | l =0, 1, ···,b,∞} be the DM-components of A(s).Fork =1, ···,r−
1, the kth monic determinantal divisor d
k
(s) and the kth monic invariant
factor e
k
(s) of A(s) are monomials given by (6.53) and (6.54).Therth monic
determinantal divisor d
r
(s) and the rth monic invariant factor e
r
(s) of A(s)
are given by (6.57)–(6.60),inwhich
¯
A
l
(s; t) is replaced by
¯
A
l
(s).
Proof. In addition to Theorems 6.3.3 and 6.3.4, note Remark 6.3.7 and the
fact that the CCF reduces to the DM-decomposition in this special case.
Remark 6.3.9. The present results on the Smith form, Theorems 6.3.4 and
6.3.8 in particular, will find direct applications in the argument on structural
controllability in §6.4. 2
Example 6.3.10. The theorems above are illustrated here for a 5×5 matrix
A(s)=
⎛
⎜
⎜
⎜
⎜
⎝
x
1
x
2
x
3
x
4
x
5
w
1
001+τ
1
s 3sτ
2
w
2
s 110τ
3
+ τ
4
s
w
3
2s
2
2s 2s 0 τ
5
s
w
4
00 0 s
2
τ
6
w
5
2s
3
2s
2
2s
2
0 s + τ
7
s
2
⎞
⎟
⎟
⎟
⎟
⎠
.
This is a mixed polynomial matrix with respect to (K, F )=(Q, Q(T )) for
T = {τ
1
,τ
2
,τ
3
,τ
4
,τ
5
,τ
6
,τ
7
}, admitting the decomposition A(s)=Q(s)+T (s)
with
Q(s)=
⎛
⎜
⎜
⎜
⎝
0013s 0
s 1100
2s
2
2s 2s 00
000s
2
0
2s
3
2s
2
2s
2
0 s
⎞
⎟
⎟
⎟
⎠
,T(s)=
⎛
⎜
⎜
⎜
⎝
00τ
1
s 0 τ
2
00 0 0τ
3
+ τ
4
s
00 0 0 τ
5
s
00 0 0 τ
6
00 0 0 τ
7
s
2
⎞
⎟
⎟
⎟
⎠
.
Note that Q(s) satisfies the stronger condition (MP-Q2) with
(r
1
, ···,r
5
)=(1, 1, 2, 2, 3), (c
1
, ···,c
5
)=(0, 1, 1, 0, 2)
in (6.4). The augmented LM-matrix
˜
A(s; t) of (6.55) is given by
6.3 Smith Form of Mixed Polynomial Matrices 361
˜
A(s; t)=
w
1
w
2
w
3
w
4
w
5
x
1
x
2
x
3
x
4
x
5
1 0013s 0
1 s 110 0
12s
2
2s 2s 00
1 000s
2
0
12s
3
2s
2
2s
2
0 s
−t
1
00τ
1
s 0 τ
2
−t
2
0000τ
3
+ τ
4
s
−t
3
0000 τ
5
s
−t
4
0000 τ
6
−t
5
0000 τ
7
s
2
.
The CCF
¯
A(s; t)of
˜
A(s; t), of which the diagonal blocks are matrices over
Q[s, t, T ], is given by
¯
A(s; t)=
C
0
C
1
C
2
C
3
C
∞
x
1
x
2
w
1
x
3
x
4
w
4
w
3
w
5
w
2
x
5
s 1 11
11 −3/s
−t
1
τ
1
s τ
2
s
2
1
−t
4
τ
6
10−2s 0
01−2s
2
s
−t
3
00 τ
5
s
0 −t
5
0 τ
7
s
2
00−t
2
τ
3
+ τ
4
s
.
Note that the diagonal blocks are polynomial matrices in s whereas a fraction
“−3/s” is contained in an off-diagonal block. The CCF consists of nonempty
tails and three square diagonal blocks. The CCF reveals that r =rankA(s)=
4(< 5). According to Theorem 6.3.4 we see that
d
4
(s)=α
4
· s
¯p
0
4
+¯p
∞
4
· (τ
1
s +1)· s
2
· (−1)
with ¯p
0
4
=0and ¯p
∞
4
= 1, where α
4
= −1/τ
1
to make d
4
(s) a monic polyno-
mial. Therefore,
d
4
(s)=s
3
· (s +1/τ
1
).
As for the other determinantal divisors, we obtain d
1
(s)=d
2
(s)=d
3
(s)=1
from (6.53) and (6.54). Hence the Smith form Σ
A
(s)ofA(s) is given by
Σ
A
(s) = diag [1, 1, 1,s
3
(s +1/τ
1
), 0].
Note that τ
1
, contained in
¯
A
1
(s; t), is the only member of T that appears in
Σ
A
(s), as predicted by Theorem 6.3.5.
Finally, we mention the matrix
ˆ
A(s; t). We choose, for instance,
