Murota K. Matrices and Matroids for Systems Analysis
Подождите немного. Документ загружается.

342 6. Theory and Application of Mixed Polynomial Matrices
the second term, deg
s
det T [I,J \ B], is equal to the maximum weight (with
respect to w
ij
) of a matching of size |I| = |J \ B| in the bipartite graph
(R
T
,C; E
T
) that covers I and J \B (see Theorem 6.2.2). Given (I,J,B) with
|I| = k and Δ(I,J,B) > −∞, we can construct an independent assignment
M such that
I = ∂
+
(M ∩ E
T
),J= ∂
−
M, B = ∂
+
(M ∩ E
Q
), (6.24)
and that M ∩E
T
is a maximum weight k-matching in the graph (R
T
,C; E
T
)
that covers I and J \B. Note that det Q[R
Q
,B] =0and|I| = k if and only
if B ∪ I ∈B
+
k
.Moreover,ω
+
k
(B ∪ I) = deg
s
det Q[R
Q
,B] by the definition,
andthereforewehaveΔ(I,J,B)=Ω
k
(M). Conversely, an independent as-
signment M with Ω
k
(M) maximum determines (I,J,B), as above, for which
Δ(I,J,B)=Ω
k
(M) holds true. Hence the maximum value of Δ(I,J,B)is
equal to that of Ω
k
(M).
Example 6.2.9. The valuated independent assignment problem associated
with a 4 × 5 LM-polynomial matrix
A(s)=
x
1
x
2
x
3
x
4
x
5
s
3
0 s
3
+1 s
2
1
0 s
2
s
2
s 0
f
1
−t
1
s
3
00α
1
α
2
s
f
2
0 −t
2
s
2
α
3
00
(6.25)
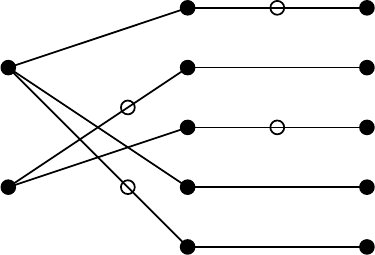
with k = 2 is illustrated in Fig. 6.1. This matrix is essentially the same
as
˜
A(s) in Example 6.2.7, but the columns and the rows are now in-
dexed as C = {x
1
,x
2
,x
3
,x
4
,x
5
} and R
T
= {f
1
,f
2
}; accordingly C
Q
=
{x
1Q
,x
2Q
,x
3Q
,x
4Q
,x
5Q
}. An optimal independent assignment
M = {(f
1
,x
5
), (f
2
,x
2
), (x
1Q
,x
1
), (x
3Q
,x
3
)}
is marked by ! in Fig. 6.1. We have I = ∂
+
(M ∩ E
T
)={f
1
,f
2
}, J =
∂
−
M = {x
1
,x
2
,x
3
,x
5
}, B = ∂
+
(M ∩ E
Q
)={x
1Q
,x
3Q
}∈B
Q
, ω
Q
(B)=5,
w(M) = 1 + 2 = 3, and therefore Ω
2
(M) = 5 + 3 = 8, which agrees with
δ
LM
2
(A)=8. 2
Theorem 6.2.8 enables us to design an efficient algorithm to compute
δ
LM
k
by specializing the general algorithmic scheme for valuated independent
assignment problems given in §5.2.13. This will be described in detail in
§6.2.6.
Remark 6.2.10. When the stronger condition (MP-Q2) may be assumed for
the matrix Q(s) of an LM-polynomial matrix A(s), the valuated independent
assignment problem reduces to a linearly-weighted independent assignment
problem. By Theorem 3.3.2, (MP-Q2) implies Q(s) = diag [s
r
1
, ···,s
r
m
] ·
6.2 Degree of Determinant of Mixed Polynomial Matrices 343
R
T
CC
Q
E
T
E
Q
f
1
f
2
x
1
x
2
x
3
x
4
x
5
x
1Q
x
2Q
x
3Q
x
4Q
x
5Q
1
w =3
s
0
R
w =1
3
2
1
0
w =0
0
0
0
w =0
Fig. 6.1. Valuated independent assignment problem for δ
LM
2
(A) of Example 6.2.9
(:arcinM, B = {x
1Q
,x
3Q
})
Q(1) · diag [s
−c
1
, ···,s
−c
n
] for some integers r
i
(i =1, ···,m)andc
j
(j =
1, ···,n). Hence ω
Q
(B)=
i∈R
Q
r
i
−
j∈B
c
j
, which is a separable valu-
ation (cf. Example 5.2.2). In place of the valuated independent assignment
problem we may consider an independent assignment problem on the same
bipartite graph G =(V
+
,V
−
; E) and the same (non-valuated) matroids
M
+
k
=(V
+
, B
+
k
)andM
−
k
=(V
−
, B
−
k
), but with the arc weight redefined as
w
ij
=
deg
s
T
ij
(s)((i, j) ∈ E
T
)
−c
j
((i, j)=(j
Q
,j) ∈ E
Q
).
Then we have
δ
LM
k
(A) = max{w(M) | M: independent assignment}+
i∈R
Q
r
i
.
This formulation under (MP-Q2) was introduced first by Murota [200] in
characterizing the dynamical degree (see also Murota [204, §27]), and then
applied to the problem of disturbance rejection by Murota–van der Woude
[242]. 2
6.2.5 Duality Theorems
The basic identities on the degree of subdeterminants presented in §6.2.3 are
recast here into novel identities of duality nature. They are obtained from
the duality result (Theorem 5.2.39) on the valuated independent assignment
problem.
344 6. Theory and Application of Mixed Polynomial Matrices
Consider the valuated independent assignment problem for δ
LM
k
(A). Let
M be an optimal independent assignment and (I,J,B) be defined by I =
∂
+
(M ∩ E
T
), J = ∂
−
M,andB = ∂
+
(M ∩ E
Q
) (cf. (6.24)), where |I| = k,
|J| = m
Q
+ k,and|B| = m
Q
.
Let ˆp : R
T
∪C ∪C
Q
→ Z be the potential function in Theorem 5.2.39. We
may assume that ˆp(j
Q
)=ˆp(j)forj ∈ C, where j
Q
∈ C
Q
denotes the copy
of j ∈ C. To see this, first note that ˆp(j
Q
) ≥ ˆp(j)forj ∈ C and the equality
holds if (j
Q
,j) ∈ M .Forj ∈ C with (j
Q
,j) ∈ M , we can redefine ˆp(j
Q
)
to be equal to ˆp(j) without violating the conditions (i) and (ii) in Theorem
5.2.39(1). Define q ∈ Z
R
T
and p ∈ Z
C
by
q
i
=ˆp(i)(i ∈ R
T
),p
j
= −ˆp(j)(j ∈ C). (6.26)
The conditions (i)–(iii) in Theorem 5.2.39(1) are expressed as follows:
deg
s
T
ij
(s) ≤ q
i
+ p
j
((i, j) ∈ E
T
), (6.27)
deg
s
T
ij
(s)=q
i
+ p
j
((i, j) ∈ M ∩E
T
), (6.28)
ω
Q
[−p](B) = max
B
∈B
Q
ω
Q
[−p](B
), (6.29)
q(I) = max
|I
|=k
q(I
), (6.30)
p(J) = max
|J
|=m
Q
+k
p(J
), (6.31)
where q(I)=
i∈I
q
i
and p(J)=
j∈J
p
j
. These conditions imply
δ
LM
k
(A) = deg
s
det Q[R
Q
,B] + deg
s
det T [I,J \ B]
= ω
Q
(B)+q(I)+p(J \ B)
= ω
Q
[−p](B)+q(I)+p(J)
= max
B
∈B
Q
ω
Q
[−p](B
) + max
|I
|=k
q(I
) + max
|J
|=m
Q
+k
p(J
). (6.32)
Thus we obtain the following theorem of Murota [233].
Theorem 6.2.11. For an LM-polynomial matrix A(s)=
.
Q(s)
T (s)
/
and an in-
teger k such that δ
LM
k
(A) > −∞, the following identity holds true:
δ
LM
k
(A) = min
q
i
+p
j
≥deg
s
T
ij
max
|I|=k
q(I) + max
|J|=m
Q
+k
p(J) + max
B∈B
Q
ω
Q
[−p](B)
,
where the minimum is taken over all q ∈ R
R
T
and p ∈ R
C
satisfying q
i
+p
j
≥
deg
s
T
ij
for all (i, j), and the minimum is attained by integer vectors q ∈ Z
R
T
and p ∈ Z
C
.
Proof. Let (I,J,B) be associated with an optimal M as above. For any (q
,p
)
with q
i
+ p
j
≥ deg
s
T
ij
(∀(i, j)), we have

6.2 Degree of Determinant of Mixed Polynomial Matrices 345
δ
LM
k
(A) = deg
s
det Q[R
Q
,B] + deg
s
det T [I,J \ B]
≤ ω
Q
(B)+q
(I)+p
(J \ B)
= ω
Q
[−p
](B)+q
(I)+p
(J)
≤ max
B
∈B
Q
ω
Q
[−p
](B
) + max
|I
|=k
q
(I
) + max
|J
|=m
Q
+k
p
(J
),
whereas the inequalities turn into equalities for (q
,p
)=(q, p), as in (6.32).
With p and q above, we can transform the matrix A(s) to another LM-
polynomial matrix that is somehow canonical with respect to δ
LM
k
.
Theorem 6.2.12. For an LM-polynomial matrix A(s)=
.
Q(s)
T (s)
/
and an in-
teger k such that δ
LM
k
(A) > −∞, there exist p ∈ Z
C
and q ∈ Z
R
T
such
that
¯
A(s)=
¯
Q(s)
¯
T (s)
=
I
m
Q
O
O diag (s; −q)
·
Q(s)
T (s)
· diag (s; −p)
satisfy
δ
LM
k
(
¯
A) = max
|B|=m
Q
deg
s
det
¯
Q[R
Q
,B] + max
|I|=|J|=k
deg
s
det
¯
T [I,J]. (6.33)
We may additionally impose either
δ
LM
k
(A)=δ
LM
k
(
¯
A) + max
|I|=k
q(I) + max
|J|=m
Q
+k
p(J) (6.34)
or that
¯
A(s) be a polynomial matrix.
Proof. Let (I,J,B) be associated with an optimal M,andp and q be defined
by (6.26). Put S(s)=(Q[R
Q
,B]·diag (s; −p
B
))
−1
, where p
B
is the restriction
of p to B, and define
ˆ
A(s)=
ˆ
Q(s)
ˆ
T (s)
=
S(s) O
O diag (s; −q)
· A(s) · diag (s; −p). (6.35)
The conditions (6.27)–(6.29) mean that
ˆ
A(s)=
⎛
⎝
BJ\ BC\J
R
Q
I
m
Q
Q
2
(s) Q
3
(s)
IT
1
(s) T
•
2
(s) T
3
(s)
R
T
\ IT
1
(s) T
2
(s) T
3
(s)
⎞
⎠
is a proper rational matrix, in which T
•
2
(s) admits a transversal consisting of
entries of degree zero. Obviously,
δ
LM
k
(
ˆ
A) = max
|B
|=m
Q
deg
s
det
ˆ
Q[R
Q
,B
] + max
|I
|=|J
|=k
deg
s
det
ˆ
T [I
,J
],
346 6. Theory and Application of Mixed Polynomial Matrices
in which all the three terms are equal to zero. This implies the first identity
(6.33). The second identity (6.34) is due to (6.32) combined with δ
LM
k
(
¯
A)=
δ
LM
k
(
ˆ
A) + deg
s
det S
−1
= ω
Q
[−p](B). To make
¯
A(s) a polynomial matrix,
replace p by p − α1 with a sufficiently large α ∈ Z, where 1 is the vector of
all components equal to one. Note that this change does not affect (6.33).
Example 6.2.13. We illustrate the above argument for the LM-polynomial
matrix A(s) of (6.25) with k = 2. The vectors p ∈ Z
C
and q ∈ Z
R
T
of (6.26)
are given by p =(−1, −1, −3, −4, −3) and q =(4, 3). Accordingly we have
¯
A(s)=
x
1
x
2
x
3
x
4
x
5
s
4
0 s
6
+ s
3
s
6
s
3
0 s
3
s
5
s
5
0
f
1
−t
1
00α
1
α
2
f
2
0 −t
2
α
3
00
,
for which (6.33) holds true with δ
LM
2
(
¯
A) = 9 = 9 + 0. All the entries of
¯
A(s)
are polynomials, and the identity (6.34) also holds true, though these two may
not be compatible in general. Recall from Example 6.2.9 that I = {f
1
,f
2
},
J = {x
1
,x
2
,x
3
,x
5
}, B = {x
1Q
,x
3Q
}. The matrix
ˆ
A(s) of (6.35) is equal to
ˆ
A(s)=
x
1
x
3
x
5
x
2
x
4
10
1
s
−s
3
−1
s
3
−1
s
010
1
s
2
1
f
1
−t
1
0 α
2
0 α
1
f
2
0 α
3
0 −t
2
0
.
In §6.2.6 we will come back to this example and explain how the vectors p
and q can be found (see the variable p in Fig. 6.4, in particular). 2
As corollaries to the above theorem we obtain the following two theorems
on the degree of the whole determinant. The first theorem shows that an
LM-polynomial matrix can be transformed so that the maximization on the
right-hand side of (6.15) in Theorem 6.2.5 may be done separately for Q-and
T -parts. The second is a similar statement for a mixed polynomial matrix
treated in Theorem 6.2.4.
Theorem 6.2.14. For a nonsingular LM-polynomial matrix A(s)=
.
Q(s)
T (s)
/
there exists p ∈ Z
C
such that
¯
A(s)=
¯
Q(s)
¯
T (s)
=
Q(s)
T (s)
· diag (s; −p)
satisfies
6.2 Degree of Determinant of Mixed Polynomial Matrices 347
deg
s
det
¯
A = max
|B|=|R
Q
|
deg
s
det
¯
Q[R
Q
,B] + max
|J|=|R
T
|
deg
s
det
¯
T [R
T
,J].
An additional condition that
¯
A(s) be a polynomial matrix may be imposed.
Proof. Apply Theorem 6.2.12 with k = m
T
= n −m
Q
to obtain p ∈ Z
C
.The
row transformation by diag (s; −q) is not necessary in the case of k = m
T
.
To make
¯
A(s) a polynomial matrix, replace p by p − α1 with a sufficiently
large α ∈ Z, where 1 is the vector of all components equal to one.
Theorem 6.2.15. For a nonsingular mixed polynomial matrix A(s)=Q(s)+
T (s), there exist p
R
∈ Z
R
and p
C
∈ Z
C
such that
¯
A(s) = diag (s; −p
R
) · A(s) · diag (s; p
C
)
satisfies
deg
s
det
¯
A = max
|I|=|J|
I⊆R,J⊆C
deg
s
det
¯
Q[I,J]+ max
|I|=|J|
I⊆R,J⊆C
deg
s
det
¯
T [R\I,C\J], (6.36)
where
¯
Q(s) = diag (s; −p
R
) · Q(s) · diag (s; p
C
),
¯
T (s) = diag (s; −p
R
) · T (s) · diag (s; p
C
).
An additional condition (i) p
R
≥ 0, p
C
≥ 0,or(ii) p
R
≤ 0, p
C
≤ 0,maybe
imposed on p
R
and p
C
.
Proof. Apply Theorem 6.2.14 to the associated LM-polynomial matrix (6.18)
to obtain ˆp ∈ Z
R∪C
. Denote by ˆp
R
and ˆp
C
the restrictions of ˆp to R and to
C, respectively. Then put p
R
= d − ˆp
R
and p
C
= −ˆp
C
, where d ∈ Z
R
is the
vector of exponents in (6.18). For the additional condition, replace p
R
with
p
R
+ α1 and p
C
with p
C
+ α1 using a suitable α ∈ Z.
Example 6.2.16. The matrix
¯
A(s) in Theorem 6.2.15 may not be a polyno-
mial matrix. Consider, for example, a 2×2 mixed matrix A(s)=Q(s)+T (s)
with
A(s)=
ss+1+t
1
s
s +1+t
2
st
3
s
,Q(s)=
ss+1
s +1 0
,T(s)=
0 t
1
s
t
2
st
3
s
.
We may take p
R
=(1, 1) and p
C
=(0, 0) to obtain
¯
A(s)=
11+1/s + t
1
1+1/s + t
2
t
3
,
¯
Q(s)=
11+1/s
1+1/s 0
,
¯
T (s)=
0 t
1
t
2
t
3
,
for which (6.36) holds true. However, it can be verified that
¯
A(s) cannot be
a polynomial matrix in (6.36). 2
See (1.37) for another example of Theorem 6.2.15.

348 6. Theory and Application of Mixed Polynomial Matrices
6.2.6 Algorithm
In §6.2.4 we have explained how to reduce the computation of δ
LM
k
(A)to
solving a valuated independent assignment problem. Here we will provide an
algorithm for δ
LM
k
(A) by adapting the augmenting algorithm of §5.2.13 for a
general valuated independent assignment problem.
The associated valuated independent assignment problem is defined on
the bipartite graph G =(V
+
,V
−
; E)=(R
T
∪C
Q
,C; E
T
∪E
Q
), where C
Q
is
a disjoint copy of C (with j
Q
∈ C
Q
denoting the copy of j ∈ C), and
E
T
= {(i, j) | i ∈ R
T
,j ∈ C, T
ij
(s) =0},E
Q
= {(j
Q
,j) | j ∈ C}.
To V
+
and V
−
are attached the valuated matroids M
+
=(V
+
, B
+
,ω
+
)and
M
−
=(V
−
, B
−
,ω
−
) defined by
B
+
= {B
+
⊆ V
+
| B
+
⊇ R
T
,B
+
∩ C
Q
∈B
Q
}, B
−
= {V
−
},
ω
+
(B
+
)=ω
Q
(B
+
∩ C
Q
)(B
+
∈B
+
),ω
−
(B
−
)=0 (B
−
∈B
−
),
where B
Q
and ω
Q
are given in (6.21) and (6.22). The arc weight w is the
same as in (6.23).
The algorithm solves VIAP(m
Q
+ k)fork =0, 1, 2, ···,k
max
by the aug-
menting algorithm of §5.2.13 to compute the value of δ
LM
k
(A) successively
for k =0, 1, 2, ···,k
max
, where k
max
is the maximum k with δ
LM
k
(A) > −∞.
Namely, the algorithm maintains a pair (M,B) of a matching M ⊆ E
T
∪E
Q
and a base B ∈B
Q
(⊆ 2
C
Q
) that maximizes
Ω
(M,B) ≡ w(M)+ω
Q
(B)=w(M ∩ E
T
)+ω
Q
(B) (6.37)
subject to the constraint that ∂
+
(M ∩E
Q
)=B and M is of a specified size.
We put
M
T
= M ∩ E
T
,M
Q
= M ∩ E
Q
.
With reference to (M, B) it constructs an auxiliary directed graph
˜
G =
˜
G
(M,B)
=(
˜
V,
˜
E) with vertex set
˜
V = R
T
∪ C
Q
∪ C and arc set
˜
E = E
T
∪
E
Q
∪ E
+
∪ M
◦
, where
E
+
= {(i
Q
,j
Q
) | i
Q
∈ B, j
Q
∈ C
Q
\ B, B − i
Q
+ j
Q
∈B
Q
},
M
◦
= {a | a ∈ M } (a: reorientation of a).
It should be emphasized that the arcs in E
+
have both ends in C
Q
and
that the arcs in M
◦
are directed from C to R
T
∪ C
Q
, i.e., ∂
+
M
◦
⊆ C and
∂
−
M
◦
⊆ R
T
∪ C
Q
. We put
M
◦
T
= {a ∈ M
◦
| ∂
−
a ∈ R
T
} = {a | a ∈ M
T
},
M
◦
Q
= {a ∈ M
◦
| ∂
−
a ∈ C
Q
} = {a | a ∈ M
Q
}.
We define the entrance S
+
⊆
˜
V and the exit S
−
⊆
˜
V by
6.2 Degree of Determinant of Mixed Polynomial Matrices 349
S
+
= R
T
\ ∂
+
M
T
= R
T
\ ∂
−
M
◦
T
,S
−
= C \ ∂
−
M = C \ ∂
+
M
◦
.
Note that no vertex in C
Q
belongs to the entrance S
+
.
We define the arc length γ = γ
(M,B)
:
˜
E → Z by
γ
(M,B)
(a)=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
−deg
s
T
ij
(s)(a =(i, j) ∈ E
T
)
deg
s
T
ij
(s)(a =(j, i) ∈ M
◦
T
)
−ω
Q
(B,i
Q
,j
Q
)(a =(i
Q
,j
Q
) ∈ E
+
)
0(a ∈ E
Q
∪ M
◦
Q
)
(6.38)
where ω
Q
(B,i
Q
,j
Q
)=ω
Q
(B − i
Q
+ j
Q
) − ω
Q
(B), compatibly with the no-
tation (5.21). By (5.23) we can compute ω
Q
(B,i
Q
,j
Q
) by means of pivoting
operations on Q(s), namely, for P (s)=S(s)Q(s) with S(s)=Q[R
Q
,B]
−1
we have ω
Q
(B,i
Q
,j
Q
) = deg
s
P
ij
(s).
Suppose there is a shortest path in
˜
G
(M,B)
from the entrance S
+
to the
exit S
−
with respect to the arc length γ, and let L be (the set of arcs on) a
shortest path from S
+
to S
−
having the smallest number of arcs. Then we
can update (M,B)to(
M,B)by
M = M −{a ∈ M | a ∈ L ∩ M
◦
} +(L ∩ (E
T
∪ E
Q
)), (6.39)
B = B −{∂
+
a | a ∈ L ∩ E
+
} + {∂
−
a | a ∈ L ∩ E
+
}. (6.40)
In fact,
M is obviously a matching with ∂
+
(M ∩E
Q
)=B and |M| = |M|+1,
and furthermore, Theorem 5.2.62 shows that
B ∈B
Q
and (M,B) maximizes
Ω
(M,B) under these constraints.
Our algorithm for δ
LM
k
(A) repeats finding a shortest path and updating
(M,B) as follows.
Outline of the algorithm
Starting from a maximum-weight base B ∈B
Q
with respect to ω
Q
and the corresponding matching M = {(j
Q
,j) | j
Q
∈ B}, repeat
(i)–(ii) below:
(i) Find a shortest path L having the smallest number of arcs from
S
+
to S
−
in
˜
G
(M,B)
with respect to the arc length γ
(M,B)
of
(6.38). [Stop if there is no path from S
+
to S
−
.]
(ii) Update (M,B) according to (6.39) and (6.40).
An initial base B of maximum value of ω
Q
can be found by the greedy
algorithm described in §5.2.4. At each stage of this algorithm it holds that
δ
LM
k
(A)=Ω
(M,B)fork = |M|−m
Q
and that (I,J,B) defined by (6.24)
gives the maximum in the expression (6.17) of δ
LM
k
(A).
As has been explained in §5.2.13, the above algorithm can be made more
efficient by the explicit use of a potential function on the auxiliary graph
˜
G =(
˜
V,
˜
E). To this end we maintain p :
˜
V → Z that satisfies

350 6. Theory and Application of Mixed Polynomial Matrices
− deg
s
T
ij
(s)+p(i) − p(j) ≥ 0((i, j) ∈ E
T
), (6.41)
−deg
s
T
ij
(s)+p(i) − p(j)=0 ((i, j) ∈ M
T
), (6.42)
p(j
Q
) − p(j) ≥ 0(j ∈ C), (6.43)
p(j
Q
) − p(j)=0 ((j
Q
,j) ∈ M
Q
), (6.44)
−ω
Q
(B,i
Q
,j
Q
)+p(i
Q
) − p(j
Q
) ≥ 0((i
Q
,j
Q
) ∈ E
+
), (6.45)
p(i) − p(k) ≥ 0(i ∈ R
T
,k ∈ S
+
), (6.46)
p(k) − p(j) ≥ 0(j ∈ C, k ∈ S
−
). (6.47)
It is remarked that the existence of such p implies the optimality of (M,B)
with respect to Ω
of (6.37). In fact, for any (M
,B
) with |M
| = |M| and
∂
+
(M
∩ E
Q
)=B
we have
w(M
)+ω
Q
(B
)=w
p
(M
)+ω
Q
[p
Q
](B
)+p(∂
+
M
T
) − p(∂
−
M
)
≤ ω
Q
[p
Q
](B)+p(∂
+
M
T
) − p(∂
−
M)
= w(M)+ω
Q
(B),
where M
T
= M
∩ E
T
, w
p
(a)=w(a) − p(∂
+
a)+p(∂
−
a), and p
Q
denotes
the restriction of p to C
Q
. Note that w
p
(M
) ≤ w
p
(M) = 0 by (6.41)–(6.44),
ω
Q
[p
Q
](B
) ≤ ω
Q
[p
Q
](B) by (6.45) and Theorem 5.2.7, p(∂
+
M
T
) ≤ p(∂
+
M
T
)
by (6.46), and p(∂
−
M
) ≥ p(∂
−
M) by (6.47).
Initially, we have M
T
= ∅ and ω
Q
(B,i
Q
,j
Q
) ≤ 0 for all (i
Q
,j
Q
) ∈ E
+
,
and therefore we can put
p(i) = max
k∈R
T
,j∈C
deg
s
T
kj
(s)(i ∈ R
T
),p(j)=p(j
Q
)=0 (j ∈ C)
(6.48)
to meet the conditions (6.41)–(6.47). In general steps, p is updated to
p(v)=p(v)+Δp(v)(v ∈
˜
V ) (6.49)
based on the length Δp(v) of the shortest path from S
+
to v with respect to
the modified arc length
γ
p
(a)=γ(a)+p(∂
+
a) − p(∂
−
a) ≥ 0(a ∈
˜
E), (6.50)
where the nonnegativity of γ
p
is due to (6.41)–(6.47). Then p satisfies the
conditions (6.41)–(6.47) (see Lemmas 5.2.65, 5.2.66, and 5.2.68).
To compute ω
Q
(B,i
Q
,j
Q
) we use two matrices (or two-dimensional ar-
rays) P = P (s)andS = S(s), as well as two vectors (or one-dimensional
arrays) base and p. The array P represents an m
Q
× n matrix of rational
functions in s over K, where P = Q at the beginning of the algorithm (Step
1 below). The other array S is an m
Q
× m
Q
matrix of rational functions in
s over K, which is set to the unit (identity) matrix in Step 1. The variable
base is a vector of size m
Q
, which represents a mapping (correspondence):

6.2 Degree of Determinant of Mixed Polynomial Matrices 351
R
Q
→ C ∪{0}. The vector p, indexed by R
T
∪ C ∪ C
Q
, represents the po-
tential function satisfying (6.41)–(6.47). We also use a scalar (integer-valued)
variable δ
Q
to compute ω
Q
(B).
The following algorithm computes δ
LM
k
(A)fork =0, 1, 2, ···,k
max
, as well
as the value of k
max
, where k
max
= −1 by convention, if rank Q(s) <m
Q
.
Algorithm for δ
LM
k
(A)(k =0, 1, 2, ···,k
max
)
Step 1: [Initialize]
M := ∅; B := ∅; δ
Q
:= 0;
base[i]:=0(i ∈ R
Q
); P[i, j]:=Q
ij
(i ∈ R
Q
,j ∈ C);
S := unit matrix of order m
Q
;
p[i] := max
k∈R
T
,j∈C
deg
s
T
kj
(i ∈ R
T
); p[j]:=p[j
Q
]:=0(j ∈ C). [cf. (6.48)]
Step 2: [Find B ∈B
Q
that maximizes ω
Q
]
While |B| <m
Q
do
{Find (h, j) that maximizes deg
s
P [h, j]
subject to base[h]=0,j
Q
∈ B,andP [h, j] =0;
If there exists no such (h, j), then stop with k
max
:= −1;
B := B + j
Q
; δ
Q
:= δ
Q
+ deg
s
P [h, j]; M := M +(j
Q
,j);
base[h]:=j; w := 1/P [h, j];
P [h, l]:=w × P [h, l](l ∈ C); S[h, l]:=w × S[h, l](l ∈ R
Q
);
P [m, l]:=P [m, l] − P [m, j] × P [h, l](m ∈ R
Q
\{h},l ∈ C \{j});
S[m, l]:=S[m, l] − P [m, j] × S[h, l](m ∈ R
Q
\{h},l ∈ R
Q
);
P [m, j]:=0 (m ∈ R
Q
\{h}) };
k := 0.
Step 3: [Construct the auxiliary graph
˜
G
(M,B)
]
δ
LM
k
(A):=δ
Q
+
(i,j)∈M ∩E
T
deg
s
T
ij
;
S
+
:= R
T
\ ∂
+
(M ∩ E
T
); S
−
:= C \ ∂
−
M; M
◦
:= {a | a ∈ M};
E
+
:= {(i
Q
,j
Q
) | h ∈ R
Q
,j
Q
∈ B, P[h, j] =0,i= base[h]};
γ(a):=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
−deg
s
T
ij
(s)(a =(i, j) ∈ E
T
)
deg
s
T
ij
(s)(a =(j, i) ∈ M
◦
T
)
−deg
s
P [h, j](a =(i
Q
,j
Q
) ∈ E
+
, base[h]=i)
0(a ∈ E
Q
∪ M
◦
Q
)
[cf. (6.38)]
where M
◦
T
= {a | a ∈ M ∩E
T
}, M
◦
Q
= {a | a ∈ M ∩E
Q
};
γ
p
(a):=γ(a)+p[∂
+
a] − p[∂
−
a](a ∈
˜
E). [cf. (6.50)]
Step 4: [Augment M along a shortest path]
For each v ∈
˜
V compute the length Δp(v) of the shortest path from S
+
to v in
˜
G
(M,B)
with respect to the modified arc length γ
p
;
If there is no path from S
+
to S
−
(including the case where S
+
= ∅ or
S
−
= ∅), then stop with k
max
:= k;
Let L (⊆
˜
E) be (the set of arcs on) a shortest path, having the smallest
number of arcs, from S
+
to S
−
with respect to the modified arc length
γ
p
;
