Murota K. Matrices and Matroids for Systems Analysis
Подождите немного. Документ загружается.

372 6. Theory and Application of Mixed Polynomial Matrices
where {f
i
| i =1, ···, 4}∪{a
i
| i =1, ···, 6}∪{b} is assumed to be alge-
braically independent over Q. (This example is taken from Matsumoto–Ikeda
[187].) The conditions (B1) and (B2) are satisfied. The DM-decomposition
of the bipartite graph G yields the horizontal tail G
0
with V
+
0
= {x
1
,x
3
,u}
and V
−
0
= {e
1
,e
3
}, and one consistent component G
1
with V
+
1
= {x
2
,x
4
}
and V
−
1
= {e
2
,e
4
}.Thes-arcs corresponding to f
3
and f
4
are contained in
G
1
, causing this system to be uncontrollable. 2
V
−
e
2
e
1
e
3
V
+
u
x
2
x
1
x
3
G
0
G
1
G
2
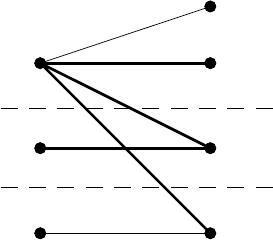
Fig. 6.6. DM-decomposition of the graph G of Example 6.4.12 (bold line: s-arc)
Example 6.4.14. Consider the descriptor system (6.65) with
F =
⎛
⎜
⎝
0000
f
1
000
0 f
2
00
f
3
000
⎞
⎟
⎠
,A=
⎛
⎜
⎝
a
1
00a
2
000a
3
0 a
4
a
5
0
0 a
6
a
7
0
⎞
⎟
⎠
,B=
⎛
⎜
⎝
b
1
0
0 b
2
00
00
⎞
⎟
⎠
,
taken from Aoki–Hosoe–Hayakawa [7]. The conditions (B1) and (B2) are eas-
ily verified to hold. The third condition (B3) is trivially met, since the whole
graph G constitutes the horizontal tail in the DM-decomposition. Therefore,
this system is structurally controllable. 2
6.4.3 Mixed Polynomial Matrix Formulation
Though the notion of structural controllability is quite appealing, it is often
doubtful from the physical point of view to assume that all the nonvanishing
entries of the coefficient matrices are independent parameters, since they usu-
ally do not stand for individual physical parameters, as has been discussed in
6.4 Controllability of Dynamical Systems 373
Chap. 3. In particular, some of the entries may be fixed or correlated num-
bers having mutual algebraic dependence. This observation has motivated
a number of generalizations and refinements in the structural approach in
control theory (see, e.g., Hayakawa–Hosoe–Hayashi–Ito [106, 107], Yamada–
Luenberger [346]).
In this section we are concerned with a combinatorial characterization of
structural controllability in the spirit of our physical observations in Chap. 3.
In particular, we consider the descriptor system (6.65) in which F , A,andB
are mixed matrices with ground field Q:
F = Q
F
+ T
F
,A= Q
A
+ T
A
,B= Q
B
+ T
B
, (6.71)
such that the set T of the nonvanishing entries of [T
F
| T
A
| T
B
] is alge-
braically independent over Q. This implies that [A − sF | B]=Q(s)+T (s)
is a mixed polynomial matrix. Furthermore, it is assumed that the matrix
Q(s) satisfies the stronger condition for the dimensional consistency.
It should be clear that assuming algebraic independence for T is equiva-
lent to regarding the members of T as independent parameters, and therefore
to considering a family of systems parametrized by those parameters in T .
A particular system in this family having algebraically independent parame-
ter values is controllable if and only if almost all members of the family are
controllable.
We formulate the above problem in more general terms for a mixed poly-
nomial matrix, following Murota [203]. Let
A(s)=Q(s)+T (s) (6.72)
be an m ×n mixed polynomial matrix of rank m with respect to (K, F ) such
that Q(s) satisfies the stronger assumption
(MP-Q2) Every nonvanishing subdeterminant of Q(s) is a monomial
over K, i.e., of the form αs
p
with α ∈ K and an integer p.
In view of (6.66) we simply say that A(s)isstructurally controllable if
the mth monic determinantal divisor of A(s) is equal to 1. This condition is
tantamount to saying that the Smith form of A(s), as a polynomial matrix
in s over F , is equal to [I
m
| O]. We put R =Row(A)andC = Col(A)and
denote the mth monic determinantal divisor of A(s)byd
m
(s). The roots of
d
m
(s) will be called the uncontrollable modes.
We shall derive a necessary and sufficient condition for structural con-
trollability together with an efficient algorithm for testing it. The proposed
algorithm is suitable for practical applications in that it is free from numeri-
cal difficulty of rounding errors and is guaranteed to run in polynomial time
in the size of the control system in question.
The existence of a zero uncontrollable mode is easy to characterize.

374 6. Theory and Application of Mixed Polynomial Matrices
Proposition 6.4.15. An m × n mixed polynomial matrix A(s) of rank m
satisfying (MP-Q2) is free from a zero uncontrollable mode if and only if there
exists (I,J) such that rank Q(0)[R \ I,C \ J] + term-rank T (0)[I,J]=m.
Proof. A(s) does not have a zero uncontrollable mode if and only if rank A(0)
= m. Then Theorem 4.2.8 establishes this.
The multiplicity of the zero uncontrollable mode is obviously equal to
o
m
(A) = min{ord
s
det A[I,J] ||I| = |J| = m}, where ord
s
denotes the
minimum degree in s of a nonzero term in a polynomial. Then, by Remark
6.2.3, it can be characterized in terms of an independent assignment problem
(see also Remark 6.2.10).
The nonzero uncontrollable modes can be treated by means of the CCF
of an LM-polynomial matrix. This is based on the fact (Theorem 6.3.4) that
the CCF corresponds to the decomposition of the determinantal divisor into
irreducible factors.
To be specific, we consider, as in (6.55), an LM-polynomial matrix
˜
A(s)=
˜
A(s; t)=
I
m
Q(s)
−diag (t
1
, ···,t
m
) T (s)
=
˜
Q(s)
˜
T (s; t)
(6.73)
associated with A(s), where t
1
, ···,t
m
are new indeterminates and t =
(t
1
, ···,t
m
). Put
˜
C = Col(
˜
A) R ∪ C. With reference to (6.4) we define
ζ :
˜
C → Z by
ζ(j)=
−r
j
(j ∈ R)
−c
j
(j ∈ C)
(6.74)
as well as the usual convention ζ(J)=
j∈J
ζ(j)forJ ⊆
˜
C.
Regarding
˜
A(s) as an LM-matrix with respect to (K[s], F (s, t)) we may
think of its block-triangular form (“CCF over a ring”) in the sense of Theorem
4.4.19, which is obtained from
˜
A(s) through a unimodular transformation
over K[s]. Let
ˆ
A(s)and
¯
A(s) be the block-triangular matrix and the CCF of
˜
A(s) as in Theorem 4.4.19. Note that
ˆ
A(s)and
¯
A(s) have identical diagonal
blocks, though they may differ in the upper-triangular part. The families of
the row sets and the column sets in the CCF are denoted respectively by
{
¯
R
k
| k =0, 1, ···,b} and {
¯
C
k
| k =0, 1, ···,b}, and the diagonal blocks by
¯
A
k
=
¯
Q
k
¯
T
k
=
¯
A[
¯
R
k
,
¯
C
k
],k=0, 1, ···,b.
In this notation, k = 0 designates the horizontal tail, whereas the vertical
tail does not exist (is empty) since rank
˜
A =2m by rank A = m. We define
J
k
= {J ⊆
¯
C
k
|
¯
Q
k
[Row(
¯
Q
k
),
¯
C
k
\ J]: nonsingular,
¯
T
k
[Row(
¯
T
k
),J]: term-nonsingular},k=1, ···,b.
For J ⊆
¯
C
k
such that
¯
T
k
[Row(
¯
T
k
),J] is term-nonsingular, we denote by
ξ
k
(J)andη
k
(J) the highest and lowest degrees in s of a nonzero term in

6.4 Controllability of Dynamical Systems 375
det
¯
T
k
[Row(
¯
T
k
),J]. Note that ξ
k
(J)andη
k
(J) can be expressed in terms of
weighted-matching problems (cf. §6.2.2).
Theorem 6.4.16. For an m × n mixed polynomial matrix A(s) of rank m
satisfying (MP-Q2), the number of nonzero uncontrollable modes is given by
b
k=1
max{ζ(
¯
C
k
\ J)+ξ
k
(J) | J ∈J
k
}−min{ζ(
¯
C
k
\ J)+η
k
(J) | J ∈J
k
}
.
Hence there exist no nonzero uncontrollable modes if and only if
max{ζ(
¯
C
k
\J)+ξ
k
(J) | J ∈J
k
} = min{ζ(
¯
C
k
\J)+η
k
(J) | J ∈J
k
} (6.75)
for each k =1, ···,b.
Proof. The determinant of
¯
A
k
(s;1) =
¯
A
k
(s; t)
8
8
t
1
=···=t
m
=1
canbeexpressed
as det
¯
A
k
(s;1) = α
k
s
p
k
·
¯
ψ
k
(s, T ), where α
k
is a nonzero constant, p
k
is a
nonnegative integer, and
¯
ψ
k
(s, T ) ∈ K[s, T ] is not divisible by s. We note
deg
s
¯
ψ
k
(s)=max{ζ(
¯
C
k
\J)+ξ
k
(J) | J ∈J
k
}−min{ζ(
¯
C
k
\J)+η
k
(J) | J ∈J
k
},
which is a corollary of Theorem 6.2.5. Then the claim follows from Theorem
6.3.4.
Remark 6.4.17. See Murota [203] as well as Murota [204, Theorem 28.1]
for an alternative formulation of the condition for structural controllability
in the form of a weighted matroid partition problem. 2
On the basis of the combinatorial characterization in Proposition 6.4.15
and Theorem 6.4.16, an efficient algorithm for testing the existence of
zero/nonzero uncontrollable modes is designed in the next section.
Theorem 6.4.16 above includes many previously known results on the
structural controllability as special cases. In particular, it is a direct gener-
alization of Theorem 6.4.7 for the case where all the nonvanishing entries of
the coefficients are taken for independent parameters. Note that the CCF
used in Theorem 6.4.16 is a generalization of the DM-decomposition used in
Theorem 6.4.7. Theorem 6.4.16 also implies the results of Hayakawa–Hosoe–
Hayashi–Ito [106] (see Murota [204, §31.1] for detail).
6.4.4 Algorithm
In this section we describe an efficient algorithm to check for the existence of
nonzero uncontrollable modes of A(s)=Q(s)+T (s) on the basis of Theorem
6.4.16, whereas the algorithm of §4.2.4 for computing the rank of an LM-
matrix can be utilized readily for the zero uncontrollable mode by Proposition
6.4.15.
376 6. Theory and Application of Mixed Polynomial Matrices
Before describing the concrete procedure for detecting nonzero uncontrol-
lable modes we will outline the basic idea in general terms. As shown in §4.2.3
and §4.4.4, the CCF of the LM-matrix
˜
A(s) of (6.73) can be computed via
the independent matching problem on a bipartite graph. The CCF can be
obtained from the strong components of a subgraph of the auxiliary graph
associated with a maximum independent matching. Moreover, the argument
in §6.2 shows that max{ζ(
¯
C
k
\ J)+ξ
k
(J)} and min{ζ(
¯
C
k
\ J)+η
k
(J)},
characterizing the existence of nonzero uncontrollable modes in Theorem
6.4.16, can be expressed in terms of independent assignment problems in
the strong component corresponding to the block
¯
A
k
of the CCF. In this way
the existence of nonzero uncontrollable modes can be found by computing
max{ζ(
¯
C
k
\ J)+ξ
k
(J)} and min{ζ(
¯
C
k
\ J)+η
k
(J)} separately by efficient
algorithms that employ arithmetic operations on rational numbers only.
It is possible to design a faster algorithm by making use of a fundamental
fact about the network flow problem. To be more specific, the condition (6.75)
is equivalent to a graph-theoretic condition that there exists in the strong
component for the block
¯
A
k
no directed cycle of nonzero length with respect
to an appropriately defined arc length. This latter condition is equivalent
further to the existence of a potential function such that the length of an arc
is the difference of the potentials of the end-vertices (see Theorem 2.2.35(2)).
The existence of such a potential function is easy to check. The objective of
this section is to describe this idea in concrete terms.
A concrete description of the algorithm for the condition (6.75) follows.
We use an auxiliary network N =(V,E,γ) with underlying graph G =(V,E)
and length function γ : E → Z, in a way consistent with the algorithm in
§4.2.4 for a mixed matrix. The vertex set V is defined as
V = V
Q
∪ V
T
=(R
Q
∪ C
Q
) ∪ (R
T
∪ C
T
),
where R
Q
=Row(Q), C
Q
= Col(Q), R
T
=Row(T ), C
T
= Col(T ), V
Q
=
R
Q
∪ C
Q
,andV
T
= R
T
∪ C
T
. The arc set E consists of five disjoint parts,
E = E
TQ
∪ E
QT
∪ E
Q
∪ E
T
∪ E
M
,
to be defined below. We denote by ϕ
Q
: R ∪C → R
Q
∪C
Q
and ϕ
T
: R ∪C →
R
T
∪ C
T
the obvious one-to-one correspondences.
Let
ˆ
I ⊆ R and
ˆ
J ⊆ C be such that Q(1)[R \
ˆ
I,C \
ˆ
J] is nonsingular
and term-rank T [
ˆ
I,
ˆ
J]=|
ˆ
I|, where such (
ˆ
I,
ˆ
J) exists by Theorem 4.2.8 since
rank A(1) = m. We define
E
TQ
= {(ϕ
T
(i),ϕ
Q
(i)) | i ∈
ˆ
I}∪{(ϕ
T
(j),ϕ
Q
(j)) | j ∈ C \
ˆ
J},
E
QT
= {(ϕ
Q
(i),ϕ
T
(i)) | i ∈ R \
ˆ
I}∪{(ϕ
Q
(j),ϕ
T
(j)) | j ∈
ˆ
J}.
Let P be the pivotal transform of Q = Q(1) with pivot
ˆ
Q ≡ Q[R \
ˆ
I,C \
ˆ
J].
Namely,
6.4 Controllability of Dynamical Systems 377
P =
R \
ˆ
I
ˆ
J
C \
ˆ
J
ˆ
Q
−1
ˆ
Q
−1
Q[R \
ˆ
I,
ˆ
J]
ˆ
I −Q[
ˆ
I,C \
ˆ
J]
ˆ
Q
−1
Q[
ˆ
I,
ˆ
J] − Q[
ˆ
I,C \
ˆ
J]
ˆ
Q
−1
Q[R \
ˆ
I,
ˆ
J]
,
(6.76)
where Row(P )=(C \
ˆ
J) ∪
ˆ
I and Col(P )=(R \
ˆ
I) ∪
ˆ
J. Note that P is a
constant matrix free from s. With reference to P we define
E
Q
= {(ϕ
Q
(i),ϕ
Q
(j)) | P
ij
=0,i∈ (C \
ˆ
J) ∪
ˆ
I,j ∈ (R \
ˆ
I) ∪
ˆ
J}.
The structure of T is represented by E
T
and E
M
. For each nonzero entry
T
ij
(s)ofT (s) we consider a pair of parallel arcs a
0
ij
and a
1
ij
with ∂
+
a
0
ij
=
∂
+
a
1
ij
= ϕ
T
(i) ∈ R
T
and ∂
−
a
0
ij
= ∂
−
a
1
ij
= ϕ
T
(j) ∈ C
T
. Putting
E
0
T
= {a
0
ij
| T
ij
=0,i∈ R, j ∈ C},E
1
T
= {a
1
ij
| T
ij
=0,i∈ R, j ∈ C},
we define E
T
= E
0
T
∪ E
1
T
. Since term-rank T [
ˆ
I,
ˆ
J]=|
ˆ
I|, the bipartite graph
(R
T
,C
T
; E
T
) with vertex set R
T
∪ C
T
and arc set E
T
has a matching M
(⊆ E
T
) such that |M| = |
ˆ
I|, ϕ
T
(
ˆ
I)=∂
+
M,andϕ
T
(
ˆ
J) ⊇ ∂
−
M. We define
E
M
as the set of reoriented arcs of M, i.e.,
E
M
= {¯a | a ∈ M},
where ¯a denotes the reorientation of a.
The length function γ : E → Z is defined with reference to r
i
(i =
1, ···,m)andc
j
(j =1, ···,n) of (6.4) as
γ(a)=
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
−r
i
if a =(ϕ
T
(i),ϕ
Q
(i)) ∈ E
TQ
,i∈
ˆ
I,
−c
j
if a =(ϕ
T
(j),ϕ
Q
(j)) ∈ E
TQ
,j∈ C \
ˆ
J,
r
i
if a =(ϕ
Q
(i),ϕ
T
(i)) ∈ E
QT
,i∈ R \
ˆ
I,
c
j
if a =(ϕ
Q
(j),ϕ
T
(j)) ∈ E
QT
,j∈
ˆ
J,
0ifa ∈ E
Q
,
−ord
s
T
ij
(s)if a ∈ E
0
T
,
−deg
s
T
ij
(s)if a ∈ E
1
T
,
−γ(a
)ifa ∈ E
M
is the reorientation of a
∈ M ⊆ E
T
.
For a nonzero entry T
ij
(s)ofT (s) with ord
s
T
ij
(s) = deg
s
T
ij
(s) (which is the
case if T
ij
(s) is a monomial in s), the pair of arcs, having the same length,
may be replaced by a single arc of the same length.
We are now ready to rephrase the condition (6.75) in terms of the network
N =(G, γ). Let V
◦
be the set of vertices of G which are not reachable to the
exit
S
−
= ϕ
T
(
ˆ
J) \ ∂
−
M ⊆ C
T
(6.77)
by a directed path. The subgraph of G induced on V
◦
is denoted as G
◦
.The
strong components of G
◦
correspond to the consistent diagonal blocks of the
CCF of
˜
A, where it is noted that the vertical tail is empty. For each strong

378 6. Theory and Application of Mixed Polynomial Matrices
component of G
◦
,say
ˆ
G =(
ˆ
V,
ˆ
E), we consider the condition that the sum of
the lengths γ(a) along any directed cycle in
ˆ
G is equal to zero, i.e.,
a∈
ˆ
C
γ(a)=0 (∀
ˆ
C : directed cycle in
ˆ
G). (6.78)
Since
ˆ
G is strongly connected, this condition is equivalent, by Theorem
2.2.35(2), to the existence of a potential function π :
ˆ
V → Z such that
γ(a)=π(∂
−
a) − π(∂
+
a)(a ∈
ˆ
E). (6.79)
Theorem 6.4.18. An m ×n mixed polynomial matrix A(s) of rank m satis-
fying (MP-Q2) has no nonzero uncontrollable mode if and only if each strong
component of the subgraph G
◦
admits a potential function π such that (6.79)
holds.
Proof. For simplicity of notation let us assume that G itself is a strong com-
ponent. We also assume for simplicity of argument that each T
ij
(s)isa
monomial in s so that each pair of parallel arcs in E
T
is replaced by a sin-
gle arc. Consider the independent assignment problem as in §6.2 to com-
pute deg
s
det
˜
A(s)for
˜
A(s) of (6.73). Then max{ζ(
¯
C
k
\ J)+ξ
k
(J)} cor-
responds to the maximum weight of an independent assignment, whereas
min{ζ(
¯
C
k
\J)+η
k
(J)} to the minimum. Hence, the condition (6.75) is tan-
tamount to saying that all the independent assignments have the same weight.
This is the case if and only if the weight of an arbitrarily chosen independent
assignment is the maximum and the minimum at the same time. By The-
orem 5.2.42, the independent assignment associated with (
ˆ
I,
ˆ
J,M) has the
maximum weight if and only if there exists no negative cycle in the auxiliary
network, whereas it has the minimum weight if and only if there exists no
positive cycle. The network N employed above is essentially the same as the
auxiliary network as defined in §5.2.10. Therefore, (6.78) is necessary and
sufficient for (6.75).
Remark 6.4.19. The potential function π of (6.79), if it exists, can be con-
structed as follows. First fix a spanning tree
ˆ
T ⊆
ˆ
E and a vertex u ∈
ˆ
V .For
each v ∈
ˆ
V ,setπ(v) equal to the length of the path in
ˆ
T connecting u to v.
Finally check for the validity of this π by verifying the condition (6.79) for
each a ∈
ˆ
E \
ˆ
T . 2
The overall computational complexity for testing for the existence of un-
controllable modes on the basis of Proposition 6.4.15 and Theorem 6.4.18 is
dominated by that for the construction of the graph G and therefore bounded
by O(n
3
log n), where m ≤ n is assumed. Note that the decomposition of G
into strong components can be done in O(|E|) time and the potential func-
tion of (6.79) for a strong component
ˆ
G =(
ˆ
V,
ˆ
E), if it exists, can be found in
time of O(|
ˆ
E|) by the procedure of Remark 6.4.19. It should be emphasized

6.4 Controllability of Dynamical Systems 379
here that the whole algorithm involves only pivoting operations on the matrix
Q(1), the entries of which are rational numbers (simple numbers such as ±1
in practical applications).
Remark 6.4.20. When the above algorithm is applied to [A − sF | B]=
Q(s)+T (s) with nonsingular A−sF ,wecanchoose
ˆ
J and M so that ϕ
T
(
ˆ
J)\
∂
−
M = ϕ
T
(U), where U = Col(B). Then the exit S
−
defined in (6.77)
coincides with ϕ
T
(U). 2
Remark 6.4.21. The graph-theoretic criterion in Theorem 6.4.7 can be de-
rived from Proposition 6.4.15 and Theorem 6.4.18 applied to the matrix
[A − sF | B]=Q(s)+T (s) with Q(s)=O. The derivation relies on the
observation of Remark 6.4.20. Note that the graph G in Theorem 6.4.7 is
identical with the subgraph (R
T
,C
T
; E
T
) in the network N, except that the
arcs are reoriented. 2
6.4.5 Examples
This section illustrates the algorithm of §6.4.4 as well as Theorem 6.4.16 by
means of two examples.
Example 6.4.22. Recall again the mechanical system (Fig. 3.5) treated in
Example 3.1.7. The matrix D(s)=[A − sF | B] is given as
D(s)=
x
1
x
2
x
3
x
4
x
5
x
6
u
w
1
−s 01 0000
w
2
0 −s 01000
w
3
−k
1
0 −sm
1
0 −101
w
4
0 −k
2
0 −sm
2
100
w
5
00 0 0−1 f 0
w
6
−ss 00010
,
which can be expressed as D(s)=Q(s)+T (s) with Q(s)andT (s) of (3.18)
and (3.19). As we have seen in Examples 3.2.2 and 3.3.1 the stronger condition
(MP-Q2) is satisfied with (r
1
, ···,r
6
)=(1, 1, 2, 2, 2, 1) and (c
1
, ···,c
7
)=
(0, 0, 1, 1, 2, 1, 2). Hence the nonsingularity of A −sF is equivalent to that of
A−F , which can be verified by the algorithm of §4.2.4. It can also be verified
that rank D(0) = 6, which means, by Proposition 6.4.15, the controllability
of the zero mode.
As for the controllability of nonzero modes, we may take
ˆ
I = {w
3
,w
4
},
ˆ
J = {x
3
,x
4
,u},andM = {(w
T
3
,x
T
3
), (w
T
4
,x
T
4
)} in accordance with Remark
6.4.20. Then the matrix P of (6.76) is

380 6. Theory and Application of Mixed Polynomial Matrices
P =
w
1
w
2
w
5
w
6
x
3
x
4
u
x
1
−10 0 0−100
x
2
0 −10 0 0 −10
x
5
00−10 000
x
6
−11 0 1−110
w
3
00−10 001
w
4
0010000
.
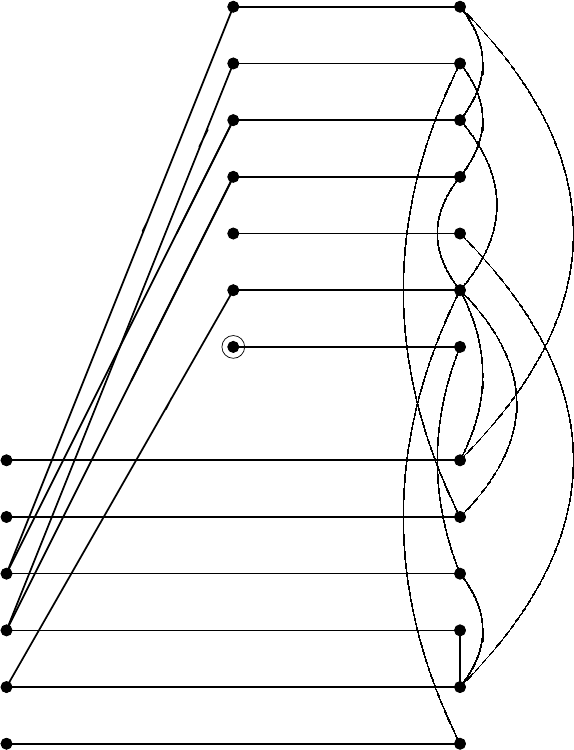
The auxiliary network N =(G, γ)=(V,E, γ) is depicted in Fig. 6.7, where
x
T
i
= ϕ
T
(x
i
), x
Q
i
= ϕ
Q
(x
i
), etc., and the associated length γ(a)is
γ(a)=
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
−2(a =(x
T
5
,x
Q
5
), (w
T
3
,w
Q
3
), (w
T
4
,w
Q
4
))
−1(a =(x
T
6
,x
Q
6
), (w
T
3
,x
T
3
), (w
T
4
,x
T
4
))
1(a =(x
T
3
,w
T
3
), (x
T
4
,w
T
4
), (x
Q
3
,x
T
3
), (x
Q
4
,x
T
4
),
(w
Q
1
,w
T
1
), (w
Q
2
,w
T
2
), (w
Q
6
,w
T
6
))
2(a =(u
Q
,u
T
), (w
Q
5
,w
T
5
))
0 (otherwise).
All the vertices except those in V
◦
= {w
T
1
,w
Q
1
,w
T
2
,w
Q
2
,w
T
6
,w
Q
6
} are reach-
able to S
−
= {u
T
}, and the subgraph G
◦
consists of three (disconnected) arcs
(w
Q
1
,w
T
1
), (w
Q
2
,w
T
2
) and (w
Q
6
,w
T
6
). Then condition in Theorem 6.4.18 is triv-
ially met, and therefore this mechanical system is structurally controllable.
2
Example 6.4.23. Consider a hypothetical descriptor system with
F =
⎡
⎣
00p
1
11p
2
00 0
⎤
⎦
,A=
⎡
⎣
1 p
3
0
001
−1 −1 p
4
⎤
⎦
,B=
⎡
⎣
p
5
0
0
⎤
⎦
, (6.80)
where {p
i
| i =1, ···, 5} is to be understood as independent parameters. The
matrix D(s)=[A −sF | B] is then a mixed matrix D(s)=Q(s)+T (s) with
Q(s)=
⎡
⎣
100
0
−s −s 1
0
−1 −10
0
⎤
⎦
,T(s)=
⎡
⎣
0 p
3
−sp
1
p
5
00−sp
2
0
00 p
4
0
⎤
⎦
,
where Row(D)={w
1
,w
2
,w
3
} and Col(D)={x
1
,x
2
,x
3
,u}. Note that Q(s)
satisfies the property (MP-Q2), admitting the expression (6.4) with, e.g.,
(r
1
,r
2
,r
3
)=(0, 1, 0) and (c
1
,c
2
,c
3
,c
4
)=(0, 0, 1, 0).
It is easy to see by inspection that A−sF is nonsingular and the zero mode
is controllable (i.e., rank D(0) = 3). For the controllability of nonzero modes,
we may take
ˆ
I = {w
1
,w
2
},
ˆ
J = {x
2
,x
3
,u},andM = {(w
T
1
,x
T
2
), (w
T
2
,x
T
3
)}
in accordance with Remark 6.4.20. Then the matrix P of (6.76) is
6.4 Controllability of Dynamical Systems 381
w
T
1
w
T
2
w
T
3
w
T
4
w
T
5
w
T
6
x
T
1
x
T
2
x
T
3
x
T
4
x
T
5
x
T
6
u
T
x
Q
1
x
Q
2
x
Q
3
x
Q
4
x
Q
5
x
Q
6
u
Q
w
Q
1
w
Q
2
w
Q
3
w
Q
4
w
Q
5
w
Q
6
-
-
-
-
-
-
?
?
?
?
?
6
6
?
?
?
6
?
?
Fig. 6.7. Auxiliary network N for the mechanical system (Example 6.4.22)
