Murota K. Matrices and Matroids for Systems Analysis

Подождите немного. Документ загружается.

442 7. Further Topics

M =(V

∪ V

, F) be the direct sum of M

and M

∗

, the dual of M

,andΠ

be the partition of the ground set V

∪V

into the pairs of the corresponding

copies. For a pair of feasible sets F

∈F

and F

∈F

, it is easy to see that

(F )=|V |−|F

| holds for F = F



∪ (V

\ F



) ∈F, where F



and F



are the copies of F

and F

. Therefore the delta-covering problem on (V,F

)

and (V, F

) is reduced to the delta-parity problem for M with the partition

Π. 2

An augmenting path algorithm is given by Geelen–Iwata–Murota [93]

for solving the delta-parity problem on linearly represented delta-matroids.

The algorithm consists of O(n) augmentations, each augmentation involv-

ing O(n

) elementary pivoting operations. Hence the time complexity of the

algorithm is O(n

) in total, where the bound can be reduced slightly with

the use of the so-called fast matrix multiplications. This algorithm can be

adapted to solve the delta-covering problem. Note in this connection that

the delta-parity problem, as well as the delta-covering problem, for a pair

of general delta-matroids is polynomially unsolvable, since it contains the

matroid-parity problem as a special case (see Remark 7.3.2 and Remark

7.3.19).

Remark 7.3.19. The delta-parity problem is a natural generalization of the

matroid parity problem, which has been explained in Remark 7.3.2. For a

matroid M =(V,ρ) with rank function ρ and a partition Π of V into lines,

let ν(M,Π) denote the optimal value of the matroid parity problem, and

δ(M,Π) be the optimal value of the delta-parity problem when M is regarded

as a delta-matroid. Then it is obvious that 2ν(M,Π)=rankM − δ(M,Π).

This shows that the matroid parity problem is a special case of the delta-

matroid parity problem. Moreover, the representation indicated in (7.51)

shows that the linear matroid parity problem is a linear delta-matroid parity

problem.

The augmenting path algorithm of Geelen–Iwata–Murota [93] for the lin-

ear delta-parity problem is based on the idea in the algorithm of Gabow–

Stallmann [83] for the linear matroid parity problem.

Also the min-max theorem (Theorem 7.3.17) for the linear delta-matroid

parity problem is closely related to the Lov´asz min-max theorem (7.44) for

the linear matroid parity problem. To see this, ﬁrst rewrite (7.44) to

δ(M,Π)=rankM − 2ν(M,Π)

= max

M→M

◦

,{V

}

'

◦

(V ) − 2



◦

)



− (ρ(V ) − ρ

◦

(V ))

(

, (7.55)

where the maximum is taken over all matroids M

◦

=(V,ρ

◦

) that are strong

quotients of M and all partitions {V

} of V that are compatible with the

partition Π. For the second term in the maximization (7.55) we can show

ρ(V ) − ρ

◦

(V ) = dist(M, M

◦

7.3 Mixed Skew-symmetric Matrix 443

where the proof for “≥” relies on the factorization theorem for strong maps

(cf. Kung [168, §8.2.B], Welsh [333, §17.4]) and that for “≤” is straightfor-

ward using (DM). The ﬁrst term in the maximization (7.55) corresponds to

odd(M

◦

,Π) in the sense that, if {V

} runs over direct sum decompositions

of M

◦

,wehave

max

}



◦

(V ) − 2



◦

)



= odd(M

◦

,Π).

This follows easily from ρ

◦

(V )=



◦

) and the fact that ρ

◦

) −

;

◦

)

is equal to 1 or 0 according to whether V

is an odd component or

not.

It should be emphasized, however, that the two min-max formulas, the

expression (7.55) and Theorem 7.3.17 (specialized to the matroid parity prob-

lem), are not identical. To be speciﬁc, we cannot assume the partition {V

}

in (7.55) to be a direct sum decomposition of M

◦

, nor can we assume the

◦

in Theorem 7.3.17 to be a strong quotient of M. This subtle point is

demonstrated by the matroid parity problem deﬁned by a linear matroid M

associated with the matrix

11000001

00110001

00001101

00000011

over F = GF(2), and a partition Π = {{v

}, {v

}}

of V = {v

, ···,v

}.WehaverankM =4,ν(M,Π) = 1, and δ(M,Π)=

2. In (7.55) we can take M for M

◦

and Π for {V

}; then ρ

◦

({v

})=

◦

({v

})=ρ

◦

({v

})=1andρ

◦

({v

}) = 2. Note that Π does not

give a direct sum decomposition of M

◦

= M. For Theorem 7.3.17 let M

the linear delta-matroid deﬁned by a skew-symmetric matrix

10010

01010

00110

00010

1000 0

0100 0

0010 0

1111 1

z 00000001

over GF(2). Fixing a base B = {v

} of the matroid M,wecan

identify the matroid M with the delta-matroid (M

\{z})/B.ForM

◦

444 7. Further Topics

/{z})/B,wehave:odd(M

◦

,Π) −dist(M, M

◦

)=3−1=2=δ(M,Π).

Note that the family of feasible sets of M

◦

is given by {{v

i ∈{1, 2},j ∈{3, 4},k ∈{5, 6}}, and that Π itself gives the ﬁnest direct

sum decomposition of M

◦

compatible with Π, where {v

}, {v

},and

} are the odd components. It should be emphasized that M

◦

can be

identiﬁed with a matroid, which, however, is not a strong quotient of M. 2

7.3.4 Rank of Mixed Skew-symmetric Matrices

The rank of a mixed skew-symmetric matrix A = Q + T can be treated

successfully by means of the delta-covering problem for the associated linear

delta-matroids.

The following identity is most fundamental, where it is recalled that

the nonsingularity of a principal submatrix of T is characterized by graph-

theoretic terms (see Proposition 7.3.8).

Lemma 7.3.20. A mixed skew-symmetric matrix A = Q + T is nonsingular

if and only if both Q[I] and T [V \I] are nonsingular for some I ⊆ V .

Proof. By the deﬁnition of Pfaﬃans we see

pf A =



I⊆V

±pf Q[I] · pf T [V \ I]. (7.56)

No cancellation can occur among terms with distinct I by virtue of the alge-

braic independence of the nonzero entries of T in the upper-triangular part.

Hence pf A = 0 if and only if pf Q[I] =0andpfT [V \I] = 0 for some I ⊆ V .

The above statement can be rephrased in terms of the union of delta-

matroids as follows.

Theorem 7.3.21. For a mixed skew-symmetric matrix A = Q+T , the delta-

matroid deﬁned by A is the union of the delta-matroids deﬁned by Q and T ,

that is, M(A)=M(Q) ∨ M(T ).

Proof. This follows from the deﬁnition (7.52) of the union and Lemma 7.3.20

applied to principal submatrices of A.

Theorem 7.3.22. For a mixed skew-symmetric matrix A = Q + T ,

rank A = max{rank Q[I]+rankT [V \ I] | I ⊆ V } (7.57)

= max{|F

||F

∈F

}, (7.58)

where M(Q)=(V, F

) and M(T )=(V,F

) are the linear delta-matroids

deﬁned respectively by Q and T .

7.3 Mixed Skew-symmetric Matrix 445

Proof. The ﬁrst identity follows from Lemma 7.3.20, whereas the second is

obtained from Theorem 7.3.21 with Lemma 7.3.15.

The rank formula (7.58) enables us to compute the rank of A = Q + T

by solving the delta-covering problem for (M(Q), M(T )). This can be done

in polynomial time (O(n

) to be speciﬁc) using arithmetic operations in K

by adapting the algorithm for delta-covering problem for a pair of linear

delta-matroids.

Remark 7.3.23. The linear matroid parity problem can be reduced to the

problem of computing the rank of a mixed skew-symmetric matrix. Given a

pair of matrices B =(b

| i =1, ···,N)andC =(c

| i =1, ···,N), the

matroid parity problem (cf. Remark 7.3.2) is to ﬁnd I ⊆ V = {1, ···,N}

of maximum cardinality such that the column vectors {b

, c

| i ∈ I} are

linearly independent. We denote by ν the optimal value (= max |I|)ofthe

matroid parity problem.

Deﬁning a mixed skew-symmetric matrix

A =

⎡

⎢

⎣

··· b

−b

0 t

−c

−t

0 00

−b

00 0 t

−c

00 −t

⎤

⎥

⎦

(7.59)

using indeterminates t

, ···,t

,wehave

rank A =2(N + ν). (7.60)

Proof of (7.60): The rank identity (7.57) yields

rank A = 2 max

(f(I)+|V \ I|),f(I) = rank (b

, c

| i ∈ I).

Hence it suﬃces to show ν coincides with ˆν = max

(f(I) −|I|). For an

optimal I of the matroid parity problem we have ν = |I| = f(I) −|I|≤ˆν.

Conversely, let I be a maximizer of f(I) −|I| that is minimal with respect to

set inclusion. Then f(I)=2|I|, since otherwise there exists i ∈ I such that

f(I \{i}) ≥ f(I) − 1, which implies that I \{i} is also a maximizer. Hence

ν ≥|I| = f (I) −|I| =ˆν.

The formula (7.60) is equivalent to a well-known identity due to Lov´asz

[178] (cf. Lov´asz–Plummer [181, Theorem 11.1.2]), which reads

rank



i=1

∧ c

)=2ν, (7.61)

446 7. Further Topics

where b ∧ c = bc

− cb

(called wedge product)andx

(i =1, ···,N)are

indeterminates. The equivalence between (7.60) and (7.61) can be shown

easily by considering a Schur complement of A and using the identity







0 t

−t 0



−1





= −

(b ∧ c)

(see Proposition 2.1.7 for Schur complement). 2

7.3.5 Electrical Network Containing Gyrators

When the branch characteristics of an electrical network are given in terms

of self- and mutual admittances Y , the network can be described by a matrix

A of the form

A =

−IY

, (7.62)

where D is a fundamental cutset matrix and R is a fundamental circuit

matrix of the underlying graph. Recall from §4.7.3 the convention that the

above system of equations describes the “free” network that is obtained after

the branches of voltage sources are contracted and those of current sources

are deleted. Since ker D =(kerR)

⊥

, the matrix A is nonsingular if and only

if DY D

is nonsingular (see Lemma 4.7.11). That is, the unique solvability

of the network is equivalent to the nonsingularity of DY D

Under the genericity assumption that the set of the nonvanishing entries of

Y is algebraically independent over Q, the matrix A above is a mixed matrix.

This makes it possible to formulate the unique solvability of the network in

terms of an independent matching problem (see also Remark 2.3.37 for a

variant of this formulation for the nonsingularity of DY D

). This genericity

assumption, though fairly reasonable in many cases, is not always justiﬁed.

An ideal element called a gyrator is commonly employed in electrical net-

work theory. It is a two-port element, the element characteristic of which is

represented as







0 g

−g 0



¯η



(7.63)

for the current-voltage pairs (ξ,η), (

ξ, ¯η) at the ports, where g = 0. Note that

the admittance matrix of a gyrator is a skew-symmetric matrix of order two.

Accordingly, it is not reasonable to impose the above-mentioned genericity

assumption on Y when the electrical network in question contains gyrators.

Gyrators are certainly ideal or artiﬁcial elements, but they play a pivotal role

in electrical network theory (cf. Rohrer [283], Saito [287]). For example, any

passive network is known to be “equivalent” to an RCG network, which is,

by deﬁnition, a network consisting of resistors, capacitors, and gyrators (and

possibly, sources).

7.3 Mixed Skew-symmetric Matrix 447

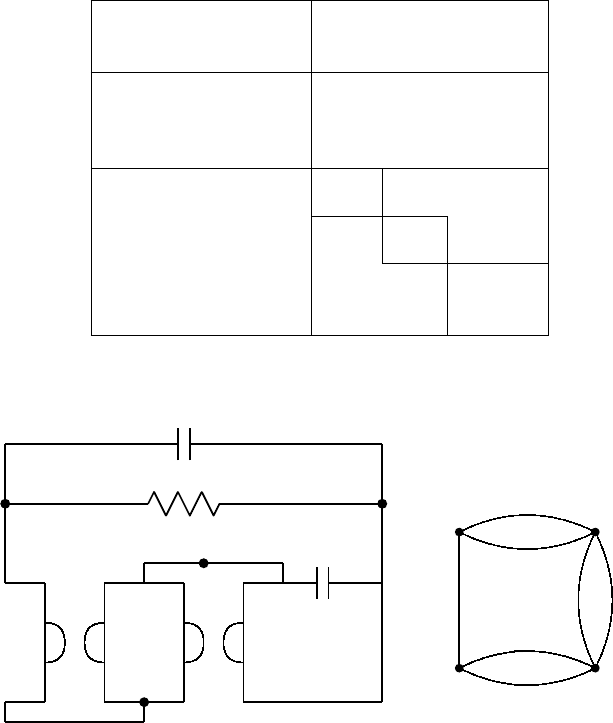
Example 7.3.24. Consider the electrical network in Fig. 7.5, taken from

Ueno–Kajitani [323], which consists of ﬁve elements: two gyrators (two pairs

of branches {1,

1} and {2,

2}), two capacitors C

and C

(branches 3 and 4),

and one resistor of conductance g

(branch 5). It is understood that voltage

sources and current sources are already contracted and deleted, respectively.

The matrix A describing this network is given by

A =

10−10010

01110−10

00101−11

1 −110−100

0 −101000

−11 00 1 10

00 00−101

−1 g

−1 −g

−1 g

−1 −g

−1 sC

−1 g

(7.64)

and the underlying graph G is depicted in the right of Fig. 7.5. 2

-  - 



Fig. 7.5. An electrical network with gyrators (Example 7.3.24)

Thus we are motivated to consider matrices of the form (7.62) such that Y

is a direct sum of a generic skew-symmetric matrix Y

and a generic diagonal

matrix Y

. Namely, we consider a matrix

448 7. Further Topics

A =

OOR

−I

O −I

, (7.65)

in which Y

is a generic skew-symmetric matrix, Y

is a generic diagonal

matrix, D

, D

, R

and R

are matrices over a ﬁeld such that [D

]and

] are of full-row rank and

ker[D

] = (ker[R

])

⊥

, (7.66)

and I

are unit matrices of appropriate dimensions. In Example 7.3.24,

for instance, we have

−g

under the reasonable assumption that {g

} is algebraically in-

dependent. It is emphasized, however, that Y

and Y

are not assumed to be

nonsingular, and that Y

is not restricted to a block-diagonal matrix consist-

ing of 2 × 2blocks.

The objective of this subsection is to show the equivalence of the nonsin-

gularity of A to that of a certain mixed skew-symmetric matrix associated

with A. This implies by Theorem 7.3.22 that the nonsingularity of A,and

hence the unique solvability of an electrical network described by A,can

be tested by the eﬃcient algorithm developed for the delta-parity/covering

problem.

Remark 7.3.25. Though any passive network is “equivalent” to an RCG

network, this does not mean that the present framework is general enough to

treat an arbitrary passive network under the reasonable genericity assump-

tion. Recall, for example, that an ideal transformer is described as







t 0

0 −1/t



¯η



When a network containing transformers are rewritten as an RCG network,

the genericity of the element t is not translated nicely to ﬁt in our present

formulation. 2

First we observe a linear algebraic fact, independent of the genericity of

and Y

. Deﬁne a skew-symmetric matrix

A by

7.3 Mixed Skew-symmetric Matrix 449

A =

⎡

⎢

⎣

OO−R

−R

O Y

OO O

−R

O OO O−Y

OO−Y

⎤

⎥

⎦

. (7.67)

Lemma 7.3.26. Let A and

A be deﬁned by (7.65) and (7.67), respectively,

where [D

] and [R

] are of full-row rank and (7.66) is assumed.

Then,

det

A = c

· (det A)

for some c =0.

Proof. First assume that Y

and Y

are nonsingular and put Z

= Y

−1

and

= Y

−1

. Deﬁne

B =











= R

+ R

Taking the Schur complement (Proposition 2.1.7) we see det

A = (det Y

det Y

)

· det S, where

S =



−R



On the other other hand, det S = (det B)

, since

det



M −N

N −M



= det[N + M] · det[N − M]

for two square matrices M and N of the same size. Finally, det B = c ·

(det Y

·det Y

)

−1

·det A for some c = 0 by Lemma 4.7.11. Therefore, det

A =

· (det A)

with nonzero c independent of Y

and Y

. This identity makes

sense regardless of the nonsingularity of Y

and Y

With the matrix A of (7.65) we associate a mixed skew-symmetric matrix

A deﬁned by

A =

⎡

⎢

⎣

OO−R

−R

OO O

−R

O OO O−Y

OO−Y

⎤

⎥

⎦

, (7.68)

where

is a copy of Y

but with a new indeterminate for each independent

entry of Y

. The matrix

A is almost the same as

A, but

A is a mixed skew-

symmetric matrix while

A is not because of the repeated occurrence of Y

In this lemma Y

can be any symmetric matrix and no genericity assumption on

and Y

is needed.

450 7. Further Topics

Lemma 7.3.27.

A is nonsingular if and only if

A is nonsingular.

Proof. Obviously, the nonsingularity of

A implies that of

A.Toshowthe

converse, we use Lemma 7.3.20. Denote by W

∪W

∪E

the column set of

A in the natural order with reference to (7.68). This serves

also as the index set for

A. We have a natural correspondences ϕ

: E

→ E

and ϕ

: E

→ E

. By the special structure of

A we can take I in Lemma

7.3.20 so that I ⊇ W

∪ W

, ϕ

(I ∩ E

)=I ∩ E

and ϕ

(I ∩ E

I ∩ E

. Consider now the expansion of the Pfaﬃan of

A in the form of

(7.56). The term corresponding to the I above has no similar terms, and

cannot be cancelled out. Hence pf

A = 0, i.e.,

A is nonsingular.

The following theorem due to Iwata [142] gives a combinatorial char-

acterization of the nonsingularity of A in (7.65). Put E

= Col(R

)and

= Col(R

Theorem 7.3.28. The following three conditions, (i) to (iii),areequivalent

for the matrix A in (7.65),whereY

is a generic skew-symmetric matrix, Y

is a generic diagonal matrix, and the orthogonality (7.66) is assumed.

(i) A is nonsingular.

(ii) There exists J ⊆ E

∪E

such that Y

[J ∩E

] is nonsingular, Y

[J ∩E

]

is nonsingular, and the submatrix of [R

] with columns in (E

∪ E

) \ J

and all rows is nonsingular.

(iii) The associated mixed skew-symmetric matrix

A deﬁned by (7.68) is

nonsingular.

Proof. The equivalence of (i) and (iii) is due to Lemma 7.3.26 and Lemma

7.3.27. The equivalence of (ii) and (iii) is implicit in the proof of Lemma

7.3.27.

The above theorem has a number of implications. First, the equivalence

of (i) and (iii) enables us to test for the nonsingularity of A by using the

algorithm for the delta-parity/covering problem. Second, the equivalence of

(i) and (ii) implies as an immediate corollary the unique solvability criterion

for electrical networks, which is explained below.

Let us consider an RCG network, though the following argument is valid

for an electrical network consisting of gyrators and other elements free from

mutual couplings. After the branches of voltage sources are contracted and

those of current sources are deleted, the network is described by a matrix A

of the form (7.65) under the genericity assumption that the element charac-

teristics are independent of one another. In this case, Y

is a direct sum of

generic skew-symmetric matrices of order two and Y

is a generic diagonal

matrix; both Y

and Y

are nonsingular. Moreover, [D

] is a fundamental

cutset matrix and [R

] is a fundamental circuit matrix of the underly-

ing graph, say G =(V, E). Note that E = E

∪ E

for E

= Col(R

)and

= Col(R

), and that E

is partitioned into pairs according to the block

structure of Y

7.3 Mixed Skew-symmetric Matrix 451

In the literature of electrical network theory a tree in G is called a proper

tree if each pair in E

is either contained in the tree or disjoint from the

tree.

Similarly, a spanning forest in G is said to be proper if each pair in E

is either contained in it or disjoint from it.

The following solvability criterion for an RCG network, essentially due to

Mili´c [194] (see also Recski [277], Ueno–Kajitani [323]), can be derived as an

immediate consequence of Theorem 7.3.28.

Theorem 7.3.29. An RCG network is uniquely solvable (under the gener-

icity assumption) if and only if there exists a proper spanning forest.

Proof. This follows from the equivalence of (i) and (ii) in Theorem 7.3.28. Note

that the submatrix of [R

] with columns in (E

∪ E

) \ J and all rows is

nonsingular if and only if J is a spanning forest, whereas the nonsingularity

of Y

[J ∩E

] imposes the properness on the spanning forest.

The connection of the solvability condition above to the matroid parity

problem was pointed out ﬁrst by Recski [276]. In the special case where

the network consists of gyrators only, the associated mixed skew-symmetric

matrix

A takes the form of (7.59), and therefore, testing for the nonsingularity

A can be reduced to a matroid parity problem, as is shown in (7.60). It

is indicated by Ueno–Kajitani [323] and Recski [277] that the solvability in

the general case can be reduced to solving polynomially many matroid parity

problems; at most (|V | + |E

|)|E|

problems by Ueno–Kajitani [323] and at

most |E

| problems by Recski [277]. Recently, it is observed by Iwata [142]

that a single matroid parity problem suﬃces, as follows.

Given a graph G =(V,E

∪ E

) with E

partitioned into pairs, we make

acopyofG, denoted G



=(V



∪ E



), and consider the direct sum of G

and G



, denoted

G =(

E), where

V = V ∪ V



E = E

∪ E



∪ E



The arc set

E is partitioned into pairs as follows: {a, b} is a pair in

E if (i)

{a, b}⊆E

and it is a pair in E

, (ii) {a, b}⊆E



and it is the copy of a

pair in E

, or (iii) a ∈ E

, b ∈ E



and they are the copies of each other. We

denote this partition of

E by

Π and call

G the duplication of G.

The observation of Iwata [142] reads as follows. Recall the notation ν(·)

for the maximum number of pairs contained in a base.

Theorem 7.3.30. A graph G has a proper spanning forest if and only if

ν(M(

G),

Π)=r for the duplication

G of G,wherer denotes the number

of arcs in a spanning forest of G. Hence, the unique solvability of an RCG

network can be determined by solving a single matroid parity problem for a

graphic matroid.

In the literature (e.g., Recski [277]) “normal tree” sometimes used as a synonym

for “proper tree.” A normal tree in an RCG network, however, often means a

proper tree that contains as many capacitors as possible.