Мухин В.И. Электротехника с основами электроники. Учебное пособие. Часть 1
Подождите немного. Документ загружается.

91
Аналогичную зависимость получим для суммарной реактивной
мощности:
ΣQ=3Q
Ф
=3I
Ф
U
Ф
sin ϕ=3
3
U
Л
I
Л
sin ϕ=
3
U
Л
I
Л
sin ϕ, ВАр. (3.11)
Суммарная полная мощность в симметричном режиме:
ΣS=S
A
+S
B
+S
C
=3S
Ф
=
3QP
22
=Σ+Σ
U
Л
I
Л
, ВА. (3.12)
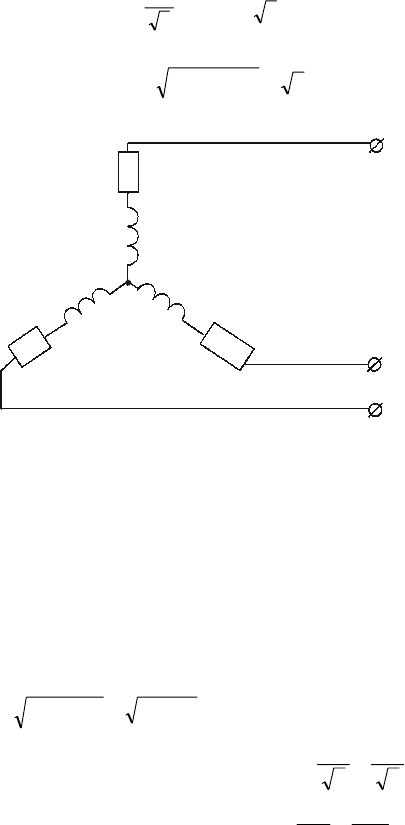
Пример 3.1.
А
R
Ф
R
Ф
R
Ф
X
L
X
L
X
L
С
В
Рис. 3.9
К трёхфазной сети с линейным напряжением 380 В подключена
симметричная нагрузка, соединённая по схеме “звезда”. Каждая из фаз
представляет собой последовательно соединённые активное (R
ф
=5 Ом)
и индуктивное (X
L
=8 Ом) сопротивления. Рассчитать активную и реак-
тивную составляющие линейных токов, а также суммарную активную,
реактивную и полную мощности. Построить векторную диаграмму на-
пряжений и токов.
Решение:
1) Рассчитаем полное сопротивление для фазы:
43.985XRZ
222
L
2
ФФ
=+=+=
Ом;
2) Определим фазное напряжение:
220
3
380
3
U
U
Л
Ф
=== В;
3) Определим ток в каждой фазе:
3,23
43,9
220
Z
U
I
Ф
Ф
Ф
===
А;
92
4) Определим сдвиг по фазе между током и напряжением:
o
58
5
8
arctg
R
X
arctg
Ф
L
===ϕ
;
5) Суммарная потребляемая активная мощность:
81435)3,23(3RI3P3P
2
Ф
2
ФФ
=••===Σ
Вт;
6) Суммарная реактивная мощность:
130298)3.23(3XI3Q3Q
2
L
2
ФФ
=••===Σ
ВАр;
7) Суммарная полная мощность:
153173,233803IU3S
ЛЛ
=••==Σ
ВА;
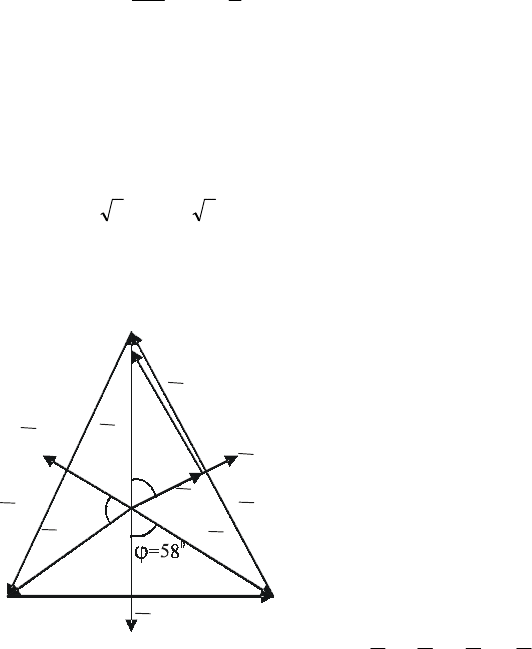
8) Для построения векторной диаграммы выбираем масштаб для
напряжения и тока. Получим следующую диаграмму (рис. 3.10):
Примечание: как ви-
дим на примере, здесь не было
необходимости применения
комплексных чисел. На диаг-
рамме можно показать распре-
деление напряжений на элемен-
тах для одной фазы А, где
U
R
=I
Ф
R
Ф
=23,3·5=116,5 В;
U
L
=I
Ф
X
L
=23,3·8=186,4 В.
Далее, имеем ввиду, что
напряжение на активном сопро-
тивлении совпадает по фазе с
током фазы, а напряжение на ин-
дуктивности опережает ток на
90°. В результате получим:
AФLR
UUUU ==+
.
При несимметричной нагрузке напряжения на фазах нагрузки
изменяются в зависимости от величины и характера нагрузки. В этом
случае расчёт электрической цепи производится с применением комп-
лексных чисел по методу узлового напряжения.
Пример 3.2.
В трёхпроводную сеть трёхфазного тока с линейным значением
ЭДС, равным 380 В, включены три группы ламп с сопротивлениями R
A
=20
А
U
L
U
R
U
AB
U
A
U
B
U
BC
U
C
U
CA
I
A
I
C
I
B
С
В
ϕ
ϕ
Рис.3.10
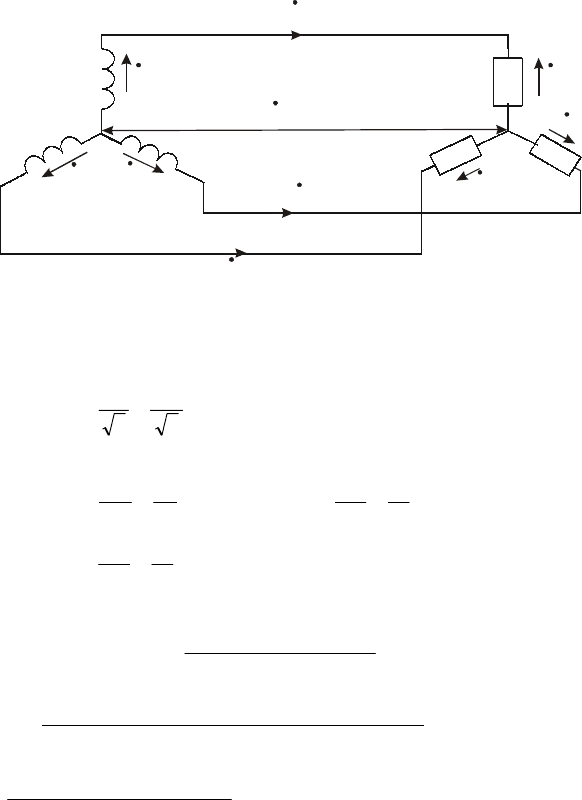
93
Ом; R
B
=10 Ом; R
C
=15 Ом, (см. рис. 3.11). Определить: 1) линейные токи
A
I
&
,
B
I
&
,
C
I
&
; 2) активную мощность трёхфазной системы.
А
О
О
’
С
В
I
A
I
B
I
C
U
C
U
B
R
B
R
C
E
A
E
B
E
C
R
A
U
A
U
N
Рис.3.11
Решение:
1) Введём обозначения:
220
3
380
3
Е
Е
Л
А
===
&
В;
o
&
120j
В
е220Е
−
=
В;
o
&
120j
е220сЕ
+
=
В;
2) Рассчитаем проводимости отдельных фаз:
05,0
20
1
R
1
Y
А
А
===
&
Ом
-1
,
1,0
10
1
R
1
Y
В
В
===
&
Ом
-1
,
067,0
15
1
R
1
Y
С
С
===
&
Ом
-1
;
3) Напряжение между точками О и О′:
CBA
CCBBAA
N
YYY
YEYEYE
U
&&&
&&&&&&
&
++
++
=
(3.13)
=
++
•+•+•
=
+−
067,01,005,0
067,02201,022005,0220
U
120j120j
N
ee
oo
&
=
++
=
+−
217,0
74,142211
120j120j
ee
oo

94
.B)75,28j96,33(
217,0
24,6j37,7
217,0
76,12j37,719j1111
217.0
120sin74,14j120cos74,14)120sin(22j)120cos(2211
−−=
−−
=
+−−−
=
=
++−+−+
=
oooo
4) Фазные напряжения на зажимах нагрузки:
)75,28j96,253()75,28j96,33(220UEU
NAA
+=−−−=−=
&&&
В;
.B)25,161j04,76(
75,28j96,33190j11075,28j96,33)120sin(220j
)120cos(220)75,28j96,33(e220UEU
120j
NBB
−−=
=++−−=++−+
+−=−−−=−=
−
o
o
o
&&&
.B)25,219j76(
75,28j96,335,190j11075,28j96,33120sin220j
120cos220)75,28j96,33(220UEU
120j
NCC
e
+−=
=+++−=+++
+=−−−=−=
o
o
o
&&&
Примечание: если дано сопротивление нулевого провода R
0
, то
в знаменателе формулы 3.13 ещё добавляется Y
0
=1/R
0
.
5) Определяем токи в линиях:
o
&&&
4,6j
AAA
e
78,12)43,1j7,12(05,0)75,28j96,253(YUI =+=•+==
А.
.А8,17
8,17)1,16j6,7(1,0)25,161j04,76(YUI
3,115j
7,244j
BBB
e
e
o
o
&&&
−
=
==−−=•−−==
o
&&&
109j
CCC
e
55,15)69,14j1,5(067,0)25,219j76(YUI =+−=•+−==
А.
Примечание: для нахождения сдвига фазы тока I
B
можно пользо-
ваться формулой
oo
7,244180
6,7
1,16
arctg
B
=+
−
−
=ϕ
, или же построить век-
тор тока на комплексной плоскости (рис. 3.12) и определить угол ϕ из
формулы:
12,2
6,7
1,16
AO
AB
tg
===α
, где α=arctg 2,12 =64,75°.
Угол ϕ
В
=α+180°=64,7+180=244,7°. Угол сдвига ϕ
С
можно вычис-
лить пользуясь формулой:
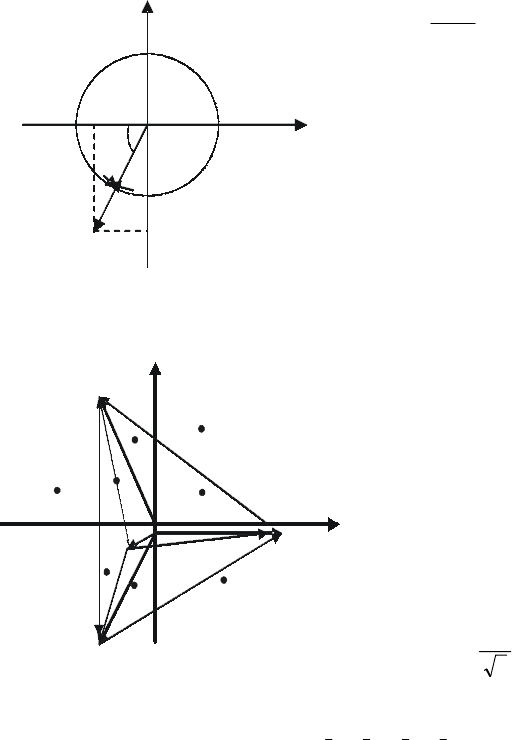
95
,109180
1,5
69,14
arctg
С
oo
=+
−
=ϕ
или же находить угол по анало-
гии с углом ϕ
В
.
На рис. 3.13 приведена
векторная диаграмма напряже-
ний к примеру 3.2. Токи
A
I
&
,
B
I
&
,
С
I
&
на диаграмме не представ-
лены.
6) Суммарная активная
мощность составит:
=++=Σ
C
2
CB
2
BA
2
A
RIRIRIP
=12,78
2
·20+17,8
2
·10+
+15,55
2
·15=10062 Вт=
=10,062 кВт. (3.14)
Чтобы напряжение
на фазах не зависело от вели-
чины и характера нагрузки
вводится четвёртый провод,
называемый нулевым или
нейтральным проводом. На-
пряжение на фазах будет оп-
ределяться по формуле:
3
U
U
Л
Ф
=
. (3.15)
Кроме того, в нулевом проводе появится ток определяемый вы-
ражением:
CBA0
IIII
&&&&
++=
, или
CBA0
IIII ++=
. (3.16)
Пример 3.3.
Дано: линейное напряжение U
Л
=380 В; R
А
=100 Ом; R
С
=200 Ом;
Х
С
=200 Ом; R
В
=60 Ом; Х
В
=80 Ом.
+j
-j
+ϕ
Β
-ϕ
B
α
+R
Ε
-R
Ε
-16,1
-7,6
O
A
B
Рис.3.12
+j
+R
Ε
O
O’
U
AB
U
N
U
A
U
B
E
B
U
BC
U
C
E
C
E
A
U
CA
Рис.3.13
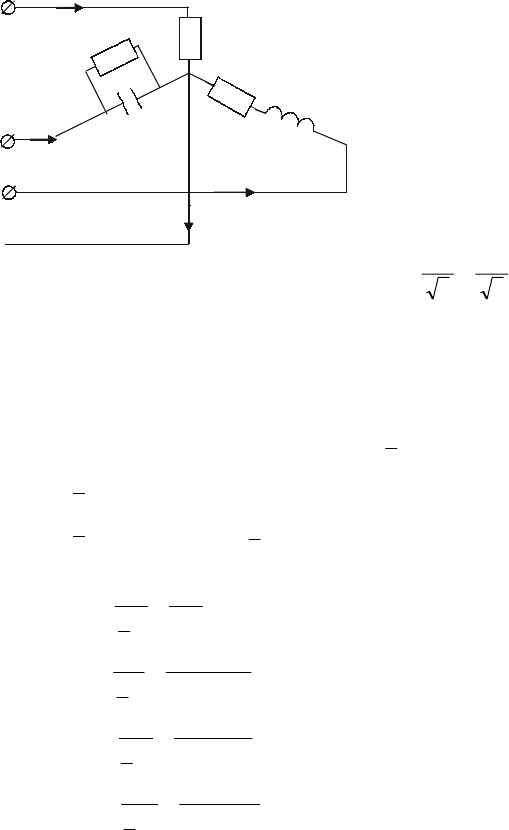
96
Рассчитать токи в
линиях
CBA
I,I,I
&&&
и ток в
нулевом проводе
0
I
&
, а также
суммарную активную, реак-
тивную и полную мощности.
Построить векторную диаг-
рамму напряжений и токов.
Решение:
1) Определим фаз-
ные напряжения:
220
3
380
3
===
Л
Ф
U
U
В;
2) Обозначим напряжения на фазах:
220=
A
U
&
В,
o
&
120
220
j
B
eU
−
=
В,
o
&
120
220
j
C
eU
+
=
В;
3) Сопротивления нагрузок в фазах:
100==
A
A
RZ
Ом;
o
53
1008060
j
BB
B
ejjXRZ =+=+=
Ом;
200
1
==
C
C
RZ
Ом;
o
90
2
200200
j
C
C
ejjXZ
−
=−=−=
Ом;
4) Определим токи в фазах:
2,2
100
200
Z
U
I
A
A
A
===
&
&
А;
o
o
o
&
&
173j
53j
120j
B
B
B
e
e
e
2,2
100
220
Z
U
I
−
−
===
А;
o
o
&
&
120j
120j
1C
C
1C
e
e
1,1
200
220
Z
U
I ===
А;
o
o
o
&
&
210j
90j
120j
2C
C
2C
e
e
e
1,1
200
220
Z
U
I ===
−
А;
Общий ток в линии:
R
Α
R
C
R
Β
X
Β
X
C
A
C
B
A
I
&
B
I
&
C
I
&
0
I
&
Рис.3.14
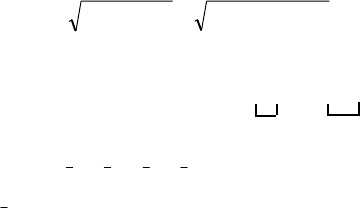
97
;A55,14,0j5,155,0j95.095,0j55,0
210sin1,1j210cos1,1120sin1,1j120cos1,1
1,11,1III
165j
210j120j
2C1CC
e
ee
o
oo
oooo
&&&
=+−=−−+−
=+++=
=+=+=
5) Ток в нулевом проводе:
;A17548,148,1132,0j47,1
4,0j49,1268,0j18,22,2165sin55,1j
165cos55,1)173sin(2,2j)173cos(2,22,2
55,12,22,2IIII
175
165j173j
CBA0
e
ee
o
o
ooo
o
oo
&&&&
∠==+−=
=+−−−=+
++−+−+=
=++=++=
−
Примечание: иногда, в литературе, пользуются сокращённой
формой записи. Например,
;A15555,1I;A1732,2I
CB
oo
&&
∠=−∠=
(3.17)
6) Суммарную активную мощность определяют по формуле:
10162001,1602,21002,2RIRIRIP
222
C
2
1CB
2
BA
2
A
=⋅+⋅+⋅=++=Σ
Вт;
7) Суммарную реактивную мощность удобно определять по фор-
муле:
2,1452422,3872001,1802,2XIXIQ
22
C
2
2CB
2
B
=−=⋅−⋅=−=Σ
ВАр; (3.18)
В фазе А нет реактивного сопротивления, поэтому нет и реак-
тивной мощности. Следует также иметь ввиду, емкостная реактивная
мощность в уравнении ставится со знаком минус, а индуктивная реак-
тивная мощность со знаком плюс.
8) Полная мощность:
3,10262,1451016QPS
2222
=+=Σ+Σ=
ВА;
9) Построение векторной диаграммы:
Исходя из величин напряжений и токов выбираем соответству-
ющие масштабы, например: М
U
50 В, М
I
0,5 А. Изобразим фазные на-
пряжения и токи на комплексной плоскости.
Проверить правильность решения можно с помощью векторной
диаграммы
CBA
IIII ++=
0
. При правильном решении полученный век-
тор
0
I
будет совпадать с расчётным
0
I
&
.
98
+j
+R
Ε
В
U
&
C
U
&
A
U
&
A
I
&
C
I
&
0
I
&
B
I
&
Рис.3.15
Эта задача может быть решена графоаналитическим методом без
применения комплексных чисел.
Решение:
1) Определим фазное напряжение:
CBA
Л
Ф
UUUВ
U
U ====== 220
3
380
3
;
2) Найдём полное сопротивление фазы:
1008060
2222
=+=+=
BBB
XRZ
Ом;
3) Определим токи в фазах:
2,2
100
220
R
U
I
A
Ф
A
=== А;
2,2
100
220
Z
U
I
B
Ф
B
=== А;
99
1,1
200
220
R
U
I
C
Ф
1C
=== А;
1,1
200
220
X
U
I
C
Ф
2C
=== А.
Y
0
X
B
U
C
U
1C
I
A
U
A
I
C
I
0
I
2C
I
B
I
A
I
′
C
I
′
Рис.3.16
Ток в нулевом проводе I
0
находим из векторной диаграммы, где
CBA
IIII ++=
0
; (3.19)
21CCC
III +=
. (3.20)
Для построения диаграммы необходимо знать, что ток в цепи,
содержащей активное сопротивление, совпадает по фазе с приложенным
напряжением, ток в цепи с ёмкостью опережает напряжение на ней, а в
цепи, содержащей последовательное соединение R
В
и Х
В
, ток отстаёт на
угол
o
53
60
80
===ϕ arctg
R
X
arctg
B
B
В
. Таким образом, проводим три век-
тора напряжений
A
U
,
B
U
,
C
U
, в соответствии с масштабом и геомет-
рически разнесённых на 120° (рис.3.16). Далее ток
A
I
совпадает с
A
U
,
М
U
50 В; М
I
0,5 А
100
ток
B
I
отстаёт от
B
U
на ϕ
в
=53°, ток
1C
I
совпадает с
C
U
, ток
2C
I
опере-
жает
C
U
на 90°. Затем находим ток
21CCC
III +=
и ток в нулевом прово-
де:
CBA
IIII ++=
0
.
Измерив геометрические длины векторов
0
I
,
C
I
и учитывая
выбранный масштаб для тока, найдём их числовые значения: I
0
=1.48 А;
I
C
=1,55 А.
Суммарные мощности ΣР, ΣQ и ΣS находим также, как это сде-
лали в предыдущем примере.
3.2.2. Анализ и расчет цепей трехфазного тока,
соединенных по схеме “треугольник”
Для выполнения расчётов электрических цепей трёхфазного
тока, соединенных по схеме треугольник, необходимо воспользоваться
уравнениями:
−=
−=
−=
BCCAC
ABBCB
CAABA
III
III
III
&&&
&&&
&&&
, (3.19) или
−=
−=
−=
BCCAC
ABBCB
CAABA
III
III
III
, (3.20)
Формулы (3.19) и (3.20) справедливы для симметричного и не-
симметричного режимов.
Условие для симметричного режима:
Z
AB
=Z
BC
=Z
CA
, (3.21)
При этом ток в линии можно находить по упрощённой формуле:
ФЛ
II3=
, (3.22)
где I
AB
=I
BC
=I
CA
=I
Ф
; I
A
=I
B
=I
C
=I
Л
. (3.23)
Суммарная активная мощность, потребляемая нагрузкой:
ϕ=Σ cosIUP
ЛЛ
3
, Вт (3.24)
Суммарная реактивная мощность:
ϕ=Σ sinIUQ
ЛЛ
3
, ВАр (3.25)
Суммарная полная мощность:
ЛЛ
IUS3=Σ
, ВА (3.26)
Рассмотрим пример расчёта трёхфазной цепи, соединённой по
схеме “треугольник”.
