Москвин Б.В. Теория принятия решений
Подождите немного. Документ загружается.


231
м 57054.5
2
77.842
- 077.84 77 40 60000 x
2
1
1
=
⋅
⋅+= .
Объекты сближаются со скоростью, определяемой соглас-
но (11.19),
x
1
2
= 40 - 2⋅77.84 = -115.68 м/сек.
Участок 2. Производится сближение объектов с постоян-
ной скоростью, равной -115.68 м/сек, при выключенной двига-
тельной установке. Длительность участка определяется согласно
(11.25):
сек. 464.32
2
40
77.84 2 - 600
2
=+⋅=τ .
Через 464.32 сек. объекты находятся на расстоянии, определяе-
мом согласно (11.20),
x
2
1
= 57054.5 - 115.68⋅464.32 = 3342 м.
Участок 3. Включается двигательная установка для того,
чтобы погасить скорость сближения КА. Длительность участка
определяется согласно (11.24)
сек. 57.84
2
40
- 77.84
3
==τ .
Через 57.84 сек. работы двигательной установки (u = 2
м/сек
2
) расстояние между объектами определяется согласно
(11.22) и равно
м. 0
2
57.842
57.84 115.68 - 3342 x
2
3
1
≈
⋅
+⋅=
Относительная скорость КА в конце участка определяется со-
гласно (11.23), и она равна
x
3
2
= -115.68 + 2⋅57.84 = 0.
Таким образом, найдено управление, позволяющее произ-
вести сближение КА за 600 сек. при минимальном расходовании
топлива.
11.2. Алгоритм Ньютона в задаче поиска оптимального по
быстродействию управления сближением КА
Принцип максимума Л.С. Понтрягина позволяет свести за-
дачу оптимального управления к краевой задаче специального
вида (см. 9.2). Будем рассматривать задачу Лагранжа с фиксиро-

232
ванными концами. Особенностью такой задачи является то, что,
если для фазовых переменных начальные условия заданы, и со-
стояние может быть найдено для любого момента времени в ре-
зультате решения задачи Коши, то для сопряженных переменных
они не заданы. Произвольное задание начальных условий сопря-
женных переменных может привести к тому, что краевые
условия
на правом конце не будут выполняться. Рассогласование в вы-
полнении таких краевых условий является функцией заданных
начальных условий для сопряженных переменных. Метод Ньюто-
на (см. 9.3) используется для решения трансцендентного уравне-
ния, в результате чего невязки в краевых условиях на правом
конце сводятся к нулю.
Применение метода Ньютона будем рассматривать
на
примере поиска оптимального по быстродействию управления в
задаче сближения КА (11.1)-(11.5).
1.
min dt J
T
0
→=
∫
.
2.
()
2
tu
txxtx ,xx
2
o2o1121
++==
,
(
)
tuxtx,ux
o222
+
=
=
.
3. u(t) ∈ G
u
= [-U
o
,+U
o
], t ∈ (0,T].
4. x(0) =
║r
o
v
o
║
т
, x(T) = ║ 0 0 ║
т
.
Из решения сопряженной системы уравнений (см. 11.1.1) и
рис.11.1 можно видеть, что момент переключения t
п
однозначно
определяется начальными условиями для сопряженных пере-
менных (ψ
1o
, ψ
2o
). Действительно,
ψ
2
(t) = ψ
2o
- ψ
1o
t
п
= 0,
тогда t
п
= ψ
2o
/ψ
1o
. Здесь ψ
1o
= const, пусть ψ
1o
= 1, тогда t
п
= ψ
2o
.
Рассмотрим, каким образом произвольное задание началь-
ных условий для сопряженных переменных (α = ψ
2o
) влияет на
выполнение краевых условий x(T) =
║ 0 0 ║
т
. При этом в качестве
невязки d(α) будем рассматривать значение
d(α)= x
1
(Т), при условии, что x
2
(Т) = 0.
Это можно пояснить следующим рисунком (11.6)
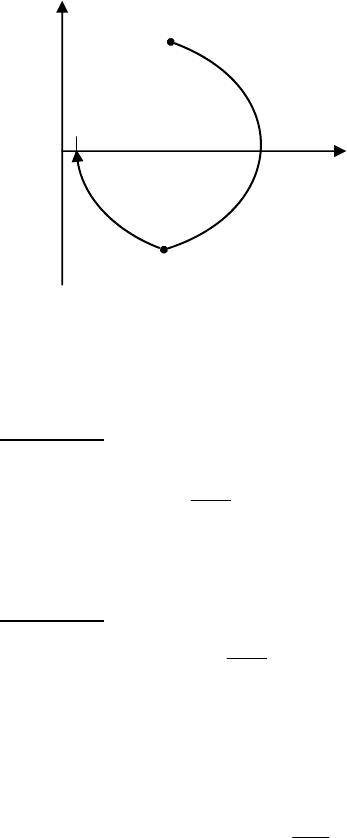
233
x
2
x(0)
α = ψ
2o
= t
п
d(α) = x
1
(Т)
u<0 T = t
п
+
t
1
x
1
(Т)
x
1
u>0
x(t
п)
Рис.11.6.
Найдем аналитическое выражение для d(α). Для этого рас-
смотрим движение системы по участкам
Участок 1:
U- u )),(t x),(t(x )v,(r
oп2п1
t
oo
=→
Π
.
В соответствии с (11.7),(11.8)
2
tU
t v r )(tx
2
по
пooп1
− += (11.28)
x
2
(t
п
) = v
o
- U
o
t
п
(11.29)
Участок 2: .U u 0); (T),(x ))(tx),(t (x
o1
t
п2п1
1
+=→
()
α=++= d
2
tU
t)(t x )(tx(T) x
2
1o
1п2п11
, (11.30)
.0tU )(tx(T) x
1oп22
=
+
= (11.31)
Подставляем (11.29) в (11.31), тогда
t
1
= t
п
- v
o
/U
o
. (11.32)
Подставляем (11.28),(11.29),(11.32) в (11.30), получаем
() ()
о
2
о
опо
2
по11
U2
v
rtv2tUtxd −++−==α
,
или, т.к. α = ψ
2o
= t
п

234
()
о
2
о
оо
2
о
U2
v
rv2Ud −+α+α−=α
. (11.33)
Тогда матрица частных производных D(α) (см.(9.13)) имеет вид
D(α) = 2v
o
- 2U
o
α. (11.34)
Пример.
Рассмотрим применение метода Ньютона в условиях при-
мера, рассмотренного в 11.1.1. Тогда r
o
= 60000 м; v
o
= 40 м/сек;
U
o
= 2 м/сек
2
.
Итерационный процесс начинается с задания произвольно-
го α
о
, и последующего уточнения его на основе формул (9.15):
(
)
(
)
kk1k
dD αα−=δ
−
,
k = 0,1,....
kk1k
δ+α=α
+
,
которое производится пока
║α
k+1
- α
k
║ больше некоторого напе-
ред заданного ε. Пусть ε = 0.01.
Подставляя заданные начальные условия в выражения
(11.33), (11.34), получим
d(α) = - α
2
+ 80α + 59600 ,
D(α) = - 4α
2
+ 80.
Проведем итерационный процесс в соответствии с алго-
ритмом Ньютона (см. 9.3). Пусть α
o
= 100.
0. α
o
= 100; тогда
248.75 = α/α−α=α=α=α ) (D) (d 320,- ) D( 47600, ) d(
ooo1oo
.
1. α
1
= 248.75; ║α
1
- α
o
║ > 0.01;
d(α
1
) = - 44253.125; D(α
1
) = -915; α
2
= 200.39 .
2. α
2
= 200.39; ║α
2
- α
1
║ > 0.01;
d(α
2
) = -4681.1; D(α) = -721.56; α
3
= 193.9 .
3. α
3
= 193.90; ║α
3
- α
2
║ > 0.01;
d(α
3
) = -82.42; D(α
3
) = -695.6; α
4
= 193.78 .
4. α
4
= 193.78; ║α
4
- α
3
║ > 0.01;
d(α
4
) = 1.02; D(α
4
) = -695.12; α
5
= 193.78 .
5. α
5
= 193.78; ║α
5
- α
4
║ < 0.01 - конец.
235
Как отмечалось в 9.3. при произвольном задании α
o
итера-
ционный процесс может расходиться. Действительно, если поло-
жить, α
o
= 300, то d(α
o
) = -96400, что превышает начальное от-
клонение, равное 60000, т.е. процесс расходится.
11.3. Оптимальное многошаговое управление выполнением
операции обслуживания КА
В 8.4.2 была поставлена задача управления выполнением
операций обслуживания КА. Рассмотрим такую задачу для одной
операции обслуживания в следующем виде
1. Функционал
min dt(t))u (t)(x
T
0
22
→+
∫
,
2. Дифференциальные связи
u(t), (t) (t)x ε=
3. Ограничения вдоль траектории:
u(t) ∈ [-U
o
, U
o
];
x(t) ≤ x
зад
.
4. Краевые условия: x(0) = 0; x(T) = x
зад
.
Здесь x
зад
- заданное состояние операции обслуживания, харак-
теризующее факт ее выполнения;
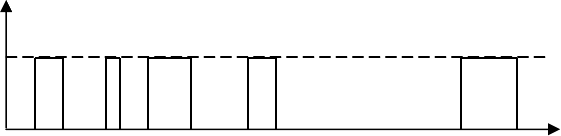
ε(t) - заданная функция, принимающая значение 1 в мо-
менты времени, когда КА попадает в зону видимости того или
иного пункта, и 0 в противном случае.
ε
1
. . . . . . . . . .
0
1 2 3 4 N t
Рис. 11.7
Проведем дискретизацию данной модели, для чего диффе-
ренциальные связи перепишем в виде
(см. 8.7)

236
()
(
)
() ()
tut
t
txttx
ε=
δ
−δ+
отсюда
x(t + δt) - x(t) = ε(t) u(t) δt
или, нумеруя интервалы, когда операция обслуживания может
выполняться, получим
x(k+1) = x(k) + u(k). (11.35)
Функционал будет иметь вид
min (k))u (k)(x J
22
1-N
0k
→+=
∑
=
. (11.36)
Ограничения вдоль траектории:
u(k) ∈ [-U
o
,+U
o
];
x(k) ≤ x
зад
; k= 0,...,N-1.
Краевые условия: x(0) = 0; x(N) = x
зад
.
Для решения такой задачи может использоваться алгоритм
динамического программирования, основанный на принципе оп-
тимальности Р. Беллмана (см. 10.4) и позволяющий получать
управление в форме синтеза.
Пусть N = 5; U
o
= 4; x
зад
= 6. Применим алгоритм динамиче-
ского программирования для решения данной задачи. Функция
Беллмана (см.(10.12)) будет иметь вид
1))).h-(x(NS h)-(Nu h)-(N(x n i m h))-(x(N S
1h-N
22
[-4,4]h)-u(N
h-N
+++=
+
∈
Вычисления начинаются с предпоследнего шага.
1). h = 1; N - h = 4; x(5) = 6.
(x(5)))S u (x min (x(4))S
5
22
u
4
++=
С учетом ограничений на управление u(4)∈[-4,4] заданное
состояние (x(5)=6) может быть достигнуто, если x(4) ∈ {2,3,4,5,6}.
Тогда, учитывая, что S
5
(x(5))= 0, получим
S
4
(2) = 2
2
+ 4
2
+ 0 = 20
S
4
(3) = 3
2
+ 3
2
+ 0 = 18
S
4
(4) = 4
2
+ 2
2
+ 0 = 20
S
4
(5) = 5
2
+ 1
2
+ 0 = 26
S
4
(6) = 6
2
+ 0
2
+ 0 = 36
237
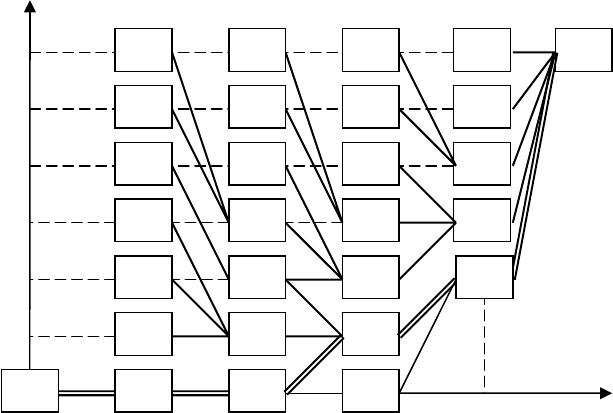
Результаты расчета значений функции Беллмана и воз-
можные переходы системы из состояния в состояние представ-
лены на следующем рисунке.
x
6
4
2
k
0 1 2 3 4
Рис.11.8.
2). h = 2; N - h = 3.
(x(4)))S u (x min (x(3))S
4
22
u
3
++=
Пусть x(3) = 6. Тогда
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
=++
−=←=++
=++
=++
=
72201636
6318936
2umin,6020436
6326136
7236036
min)6(S
3
Далее x(3) = 5;
24
36
28
23 23
31
27
23
23
27
23
22
24
26
36
18
20
0 60
46
35 43
56
72 76
60
47
20
238
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=++
=
.........................
4718425
1umin,4620125
5126025
6236125
min5S
3
Теперь x(3) = 4;
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=
.........................
4020416
1umin,3518116
3620016
........................
min4S
3
x(3) = 3;
()
⎪
⎩
⎪
⎨
⎧
=++
=←=++=
302019
0umin,271809
.......................
min3S
3
Дальнейшие вычисления производим аналогично предыдущим.
()
⎪
⎩
⎪
⎨
⎧
=++
+=←=++=
242004
1umin,231814
......................
min2S
3
()
⎪
⎩
⎪
⎨
⎧
+=←==+
=++=
1umin,222011
231841
.....................
min1S
3
()
⎪
⎩
⎪
⎨
⎧
+=←=++
=++=
2umin,242040
271890
......................
min0S
3
3). h = 3; N-h = 2.
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=++
=++
=
75231636
3umin,7227936
7535436
8346136
9660036
min6S
2
239
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=
.........................
5723925
2umin,5627425
6135125
........................
min5S
2
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=
.........................
4722916
2umin,4323416
4427116
........................
min4S
2
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=++
=++
−=←=++
=
422499
352249
1umin,332319
......................
min3S
2
()
⎪
⎩
⎪
⎨
⎧
−=←=++
=←=++=
1umin,272214
0umin,272304
........................
min2S
2
()
⎪
⎩
⎪
⎨
⎧
=++
=←=++=
262411
0umin,232201
......................
min1S
2
()
⎪
⎩
⎪
⎨
⎧
=++
+=←=++=
242400
1umin,232210
......................
min0S
2
4). h = 4; N-h = 1.
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=++
=++
=
79271636
3umin,7631936
8343436
9356136
10872036
min6S
1
240
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=++
=
6127925
2umin,6031425
6943125
8156025
........................
min5S
1
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=++
=
4823916
2umin,4727416
4831116
5943016
........................
min4S
1
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=++
=
412399
2umin,362349
372719
403109
......................
min3S
1
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=++
−=←=++
=++
=
312344
1umin,282314
312704
......................
min2S
1
()
0umin,
352311
242301
......................
min1S
1
=←
⎪
⎩
⎪
⎨
⎧
=++
=++=
()
⎪
⎩
⎪
⎨
⎧
=←=++
=++=
0umin,232300
242310
......................
min0S
1
5). h = 5; N-h = 0. Исходное состояние x(0) = 0 - задано, тогда
рассчитывается значение
()
⎪
⎩
⎪
⎨
⎧
=←=++
=++=
0umin,232300
252410
......................
min0S
0
