Москвин Б.В. Теория принятия решений

Подождите немного. Документ загружается.

211

только от того, каково конкретное состояние динамической сис-

темы. Поэтому для любого допустимого состояния x(t), которое

приняла динамическая система в результате того или иного

внешнего воздействия, известно управление, позволяющее из

данного состояния x(t) достигать заданного конечного состояния

наилучшим образом. Интуитивно это и понятно, действительно,

оптимальное управление в момент t зависит от состояния систе-

мы

, а не от предыстории процесса (начального состояния и того,

каким образом происходило движение системы до момента t).

Математически задачу синтеза можно сформулировать

следующим образом. Необходимо найти функцию управления

u(t,x(t)), t ∈ T = (t

], доставляющую минимум функционалу

J(t,x,u) → min , (10.1)

и удовлетворяющую ограничениям вдоль траектории

u(t,x(t)) ∈G

⊆ R

, (10.2)

и которая переводит динамическую систему

x(t))u(t,x,(t, (t)x ϕ=



) (10.3)

в конечное состояние

x(t

) ∈ E

(10.4)

из некоторого начального состояния.

Сформулированная задача похожа на задачу поиска опти-

мального программного управления (8.25)-(8.28). Существенным

отличием является то, что в задаче синтеза значения x(t

) и t

являются произвольными. Следовательно, необходимо постро-

ить управление, переводящее систему (10.3) в конечное состоя-

ние x(t

)∈E

из любого начального состояния x(t

) для любого

момента времени t

В общем случае задача синтеза (т.е. вопрос о существова-

нии управления в форме синтеза и способы его нахождения) не

решена.

10.2. Синтез управления в линейных динамических

системах

Наиболее простыми задачами синтеза оптимального

управления, поставленными в 10.1, являются задачи синтеза ли-

нейных (8.5) систем с линейным или квадратичным функциона-

лом. Для таких систем выполняются условия теоремы существо-

вания и единственности, т.е. для каждого x

=x(t

) существует (и

только одно) управление u(t,x

), переводящее систему из со-

стояния x

в заданное состояние x

= x(t

212

Для любого момента времени τ∈(t

] управление u(t,x

рассматриваемое на интервале (τ,t

] должно быть оптимальным,

тогда можно обозначить

u(τ,x

)= v(x(τ)).

В этом случае (8.4) можно переписать

. v(x) B(t) x A(t) x



Решение данного уравнения с произвольно заданным x

позво-

ляет найти функцию v(x), которая синтезирует оптимальное

управление, переводящее систему из x

в x

. В нахождении та-

кой функции v(x) и заключается задача синтеза для линейных

систем.

Рассмотрим особенности синтеза оптимального управле-

ния для линейной системы в задаче Лагранжа с квадратичным

функционалом

() () () () ()

()

min dt u R u x Q x

u) x,J(

тт

→ττ+τττ=

∫

здесь Q(t) - неотрицательно-определенная симметрическая мат

рица;

R(t) - положительно определенная симметрическая матри-

ца для ∀t.

Тогда x

(t)Q(t)x(t) ≥ 0, u

(t)R(t)u(t) > 0 при ∀t ∈ (t

В соответствии с принципом максимума Л.С. Понтрягина

оптимальное управление в любой момент времени находится,

исходя из максимизации функции Гамильтона (8.43)

B(t)u A(t)x R(t)uu

Q(t)x x

ттт

ψ+ψ+ψ+ψ= ,

или, транспонируя обе части равенства,

ψ+ψ+ψ+ψ= B(t)uA(t) x R(t)uu

x Q(t) x

ттт

Обозначим

(

)

n1,..., i ,

(t)p

= .

Тогда в соответствии с (8.38)

n1,..., i ,

- p

iоi

=ψ=ψ



Откуда

213

.pt- x Q(t) - p

)(Α=



(10.5)

Оптимальное управление должно доставлять максимум

функции Гамильтона. Необходимым условием этого является ра-

венство нулю частной производной гамильтониана по управле-

нию, откуда

R(t) u + B

(t) p = 0.

Тогда

u = - R

-1

(t) B

(t) p.

Подставляя последнее выражение для управления в диф-

ференциальные уравнения (8.4), описывающие изменение со-

стояния, получим

pt(t)BB(t)R - A(t)x x

т-1

)(=



. (10.6)

Будем искать неизвестную функцию p(t) в виде

p(t) = K(t) x(t), (10.7)

где K(t) - неизвестная матрица размерности n×n.

Тогда (10.6) можно переписать в виде

(

)

xt(t)BB(t)R - A(t)x x

т-1

Κ=



Подставляя (10.7) в (10.5), с учетом последнего выражения

можно получить

(t)K(t)x. -Q(t)x -

(t)K(t)x (t)BK(t)B(t)R -K(t)A(t)x K(t)x xK(t) (t)x K

т-1

Α=

=+=+



Отсюда неизвестная в (10.7) матрица K(t) должна удовлетворять

матричному дифференциальному уравнению вида

(

)

).( )(Κ)Β)()(Β)(Κ + )(Κ=

−1

tQ-tt(tRtttt A- K(t)A(t) - (t)K

тт



Данное нелинейное матричное дифференциальное урав-

нение, известное как уравнение Риккати, позволяет найти матри-

цу K(t) для любого момента времени t∈(t

] при начальных ус-

ловиях, вытекающих из условий трансверсальности. Тогда опти-

мальное управление u*(t) для состояния x(t) определяется как

u*(t) = - R

-1

(t) B

(t) K(t) x(t).

214

Для стационарной линейной динамической системы, опи-

сываемой уравнениями (8.5), дифференциальное уравнение Рик-

кати превращается в нелинейное матричное уравнение вида

KA + A

K - KBR

-1

K + Q = 0.

Решение уравнений Риккати базируется, как правило, на

использовании итеративных численных методов.

10.3. Синтез управления в рекуррентных системах.

Принцип оптимальности. Беллмана.

На основе поставленной в 8.7 задачи оптимального про-

граммного управления рекуррентными системами (8.56)-(8.59)

может быть сформулирована задача синтеза в следующем виде

()

min x(k)u(k,(x(k),F u)J(x,

1-N

→=

∑

, (10.8)

x(k+1) = f(x(k),u(k),x(k)), k = 0,...,N-1, (10.9)

u(k,x(k)) ∈ G

⊆ R

, k = 0,...,N-1, (10.10)

x(N) = x

. (10.11)

Для поиска оптимального управления u*(k,x(k)) в рекур-

рентных системах часто используются, алгоритмы основанные на

принципе оптимальности Р.Беллмана. Принцип оптимальности,

сформулированный для непрерывных систем, представляет со-

бой развитие принципа причинности для динамических систем

(см.8.1). Приведем формулировку принципа оптимальности и не-

которые следствия, вытекающие из него и поясняющие данный

принцип.

Принцип оптимальности.

Оптимальное управление в любой момент времени t, обла-

дает тем свойством, что каково бы ни было начальное состояние

динамической системы и управления в моменты времени, пред-

шествующие t, последующие управления должны быть опти-

мальны относительно состояния динамической системы в момент

времени t.

215

Следствие 1.

Оптимальное управление в любой момент времени t не зави-

сит от предыстории системы и определяется только состоянием

системы в момент t и целью управления.

Следствие 2.

В любой момент времени t (t0≤t<t

) участок оптимальной траек-

тории от x(t) до (t

) сам по себе является оптимальной траектори-

ей.

Следствие 3.

Если в некоторый момент времени управление не опти-

мально, то последствия этого отклонения от оптимального управ-

ления нельзя исправить в будущем.

Поясним принцип оптимальности в задаче (10.8)-(10.11).

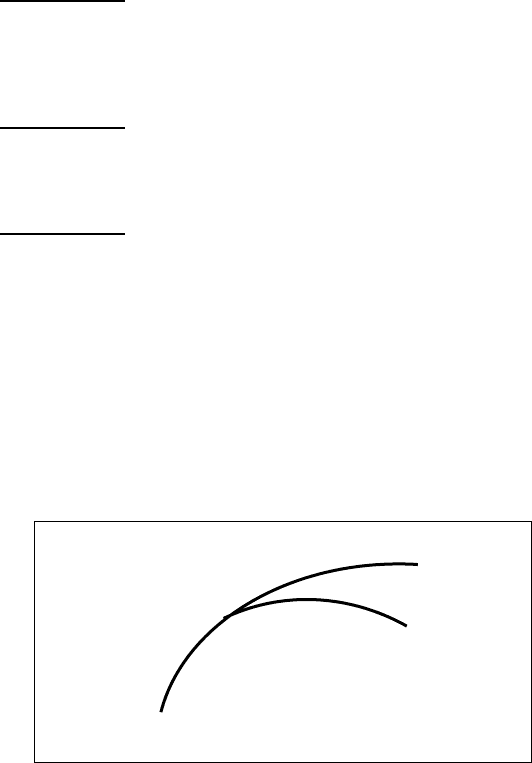
Пусть имеется (см. рис.10.1) оптимальная траектория, переводя-

щая систему из состояния x(0) в состояние x(N) и доставляющая

минимум функционалу J(x,u). Пусть точка x(s) разбивает рас-

сматриваемую траекторию на два

участка: участок 1 - x(k),

k=0,...,s-1; участок 2 - x(k), k=s,...,N. Участок 2 может рассматри-

ваться и как самостоятельная траектория. Эта траектория будет

оптимальной, если она доставляет минимум функционалу.

Рис.10.1.

В соответствии со следствием 2 принципа оптимальности -

участок 2 оптимальной траектории 1-2 сам по себе является оп-

тимальной траекторией.

Предположим противное, пусть существует другая траекто-

рия 3, отличная

от траектории 2 и доставляющая функционалу

2 x(N)

x(s) 3

x(0)

216

J(x,u) значение, меньшее, чем на траектории 2. Но тогда на ин-

тервале от 0 до N оптимальной будет не траектория 1-2, а траек-

тория 1-3. Последнее противоречит исходному предположению

об оптимальности траектории 1-2. Следовательно, участок 2

должен быть оптимальной траекторией, как это и следует из

принципа оптимальности.

На основе приведенного принципа оптимальности Р. Белл-

маном был разработан алгоритм

динамического программирова-

ния, показавший достаточно высокую эффективность в задачах

оптимизации рекуррентных систем и позволяющий получать оп-

тимальное управление в форме синтеза.

10.4. Алгоритм динамического программирования

Пусть состояние x(k) на любом шаге k, k=1,...,N-1 может

принимать значение из конечного множества состояний (на шаге

N в соответствии с (10.11) это множество состоит из одного эле-

мента x(N)=x

); обозначим множество различных состояний на

шаге k, как X

. Отметим, что число таких состояний может быть

достаточно велико, так, например, если x(k) - вектор, состоящий

из четырех компонент, и каждая компонента может принимать

всего 3 значения, то при любом k значение ⎜X

⎜ = 3

= 81.

Суть алгоритма динамического программирования состоит

в том, что, построение оптимального управления, как функции

состояния, производится из конца траектории к началу. Начиная с

предпоследнего (k = N -1) шага, для каждого допустимого состоя-

ния x(k) (число которых равно ⎜X

⎜) рассчитывается оптимальное

управление u*(k,x(k)), которое согласно принципу оптимальности

соответствует оптимальной траектории x*(k).

Итак, пусть на шаге (N-1) система находится в некотором

состоянии x(N-1), тогда оптимальное управление u*(N-1,x(N-1))

должно в соответствии с (10.9)-(10.11) переводить систему в со-

стояние x(N) = x

и доставлять минимум функционалу (10.8), т.е.

оно находится в результате решения задачи

n i m 1)))-x(N1,-u(N1),-F(x(N

G1))-x(N1,-u(N ∈

→

Обозначим минимальное значение функционала через

N-1

(x(N-1)), тогда последнее выражение можно переписать в ви-

де

217

()

(

)

1))- x(N1,-u(N 1),-x(N F min 1)-x(N S

G1))-x(N1,-u(N

1-N

∈

, (10.11)

При фиксированном значении x(N-1) минимизируемая функция в

(10.11) зависит только от u(N-1,x(N-1)), откуда и находится опти-

мальное управление u*(N-1,x(N-1)).

Рассмотрим теперь предыдущий интервал, шаг (N-2). Пусть

система находится в состоянии x(N-2), тогда задачу поиска опти-

мального управления в точке (N-2), с учетом (10.11), (10.8) можно

представить в виде

()

()()

1)))- x(N1,-u(N 1),-x(N F2))- x(N2,-u(N 2),-x(N (F min

2)-x(N S

G1))-x(N1,-u(N

G2))-x(N2,-u(N

2-N

∈

Поскольку первое слагаемое под знаком минимума не зависит от

состояния и управления на шаге (N-1), то последнее выражение

можно переписать в виде

1)))).-x(N1,-u(N1),-F(x(N n i m

2)))-x(N2,-u(N2),-F(x(N ( n i m 2))-(x(NS

G1))-x(N1,-u(N

G2))-x(N2,-u(N

2-N

∈

Второе слагаемое в соответствии с (10.11) равно S

N-1

(x(N-1)), то-

гда

1)))-(x(NS2)))-x(N2,-u(N2),-(F(x(Nn i m 2))-(x(NS

1-N

G2))-x(N2,-u(N

2-N

∈

Тогда в целом для произвольного шага (N-h) значение функции

N-h

(x(N-h))

1)))h-(x(NSh)))-x(Nh,-u(Nh),-(F(x(Nn i m

h))-(x(NS

1h-N

Gh))-x(Nh,-u(N

h-N

++=

∈

(10.12)

или с учетом (10.9)

h))))-u(Nh),-x(N((fSh)))-x(Nh,-u(Nh),-(F(x(Nn i m

h))-(x(N S

1h-N

Gh))-x(Nh,-u(N

h-N

∈

(10.13)

В выражении (10.13) поиск минимума функции S

N-h

(x(N-h))

выполняется по одной переменной u(N-h) = u(N-h,x(N-h)). Полу-

ченное при этом значение u(N-h) и будет искомым оптимальным

управлением, найденным, как функция состояния u*(N-h,x(N-h)).

218

Функция S

N-h

(x(N-h)) часто называется функцией Б е л л -

м а н а, а уравнение (10.13) р е к у р р е н т н ы м у р а в н е -

н и е м Б е л л м а н а.

Итак, начиная с шага N-1 (h=1) находится оптимальное

управление u*(N-h,x(N-h)),

которое вычисляется, исходя из ми-

нимизации функции Беллмана S

N-h

(x(N-h)); процесс вычислений

заканчиваются, когда h = N.

Замечание.

В ситуациях, когда задано исходное состояние x(0), можно

вычислить оптимальное программное управление, как функцию

шага k=0,..., N-1 (k=N-h). Действительно, поскольку известно оп-

тимальное управление в форме синтеза u*(N-h,x(N-h)), h=1,..,N,

то при h=N (k=0) и известном состоянии x(0) можно вычислить

оптимальное управления u*(0). Тогда из выражения (10.9) можно

определить состояние системы x(1) (при k=1 (h=N-1)). Для со-

стояния x(1) выбирается оптимальное программное управление

u*(1), уже рассчитанное ранее.

Теперь из (10.9) можно найти со-

стояние x(2) и так далее... Таким образом, формируется опти-

мальное программное управление u*(k), k=0,..., N-1.

Алгоритм.

0). Исходное состояние h = 1. Конечное состояние системы

задано x(N)=x

. Система находится в состоянии x(N-h) = x(N-1);

N-h+1

(x(N-h+1))) = S

(x(N)) = 0; X

N-h+1

= {x(N)}

1). Рассчитывается множество состояний X

N-h

, число которых

равно ⎜X

N-h

⎜.

2). Для каждой пары состояний x(N-h)∈X

N-h

и x(N-h+1)∈X

N-h+1

находятся различные управления u(N-h,x(N-h))∈G

, позволяю-

щие перевести систему из состояния x(N-h) в состояние x(N-

h+1). Для каждого такого управления рассчитывается значение

функции

Z(x(N-h),u(N-h,x(N-h)),x(N-h+1)) =

= (F(x(N-h),u(N-h,x(N-h))) + S

N-h+1

(x(N-h+1))) .

3). Производится выбор оптимального управления из условия

1))h-x(Nh)),-x(Nh,-u(Nh),-Z(x(N n i m arg h))-x(Nh,-(N *u

h))-h,x(N-u(N

Вычисляется значение функции Беллмана

219

1))h-x(Nh)),-x(Nh,-u(Nh),-Z(x(N n i m h))-(x(NS

h))-x(Nh,-u(N

h-N

В результате выполнения данного шага для каждого допустимого

в момент (N-h) состояния x(N-h) вычисляется оптимальное

управление u*(N-h,x(N-h)), состояние x(N-h+1), в которое перей-

дет система под воздействием данного управления, и значение

функции Беллмана S

N-h

(x(N-h)).

4). h = h + 1. Если (N - h) < 0 - процесс счета заканчивается; в

противном случае производится переход на шаг 1.

Рассмотренный алгоритм динамического программирова-

ния может быть распространен на задачи синтеза оптимального

управления для непрерывных динамических систем, описывае-

мых дифференциальными уравнениями (доказательство этого

было проведено В.Г.Болтянским). При этом рекуррентное урав-

нение (10.13) преобразуется в нелинейное дифференциальное

уравнение в

частных производных. При выполнении определен-

ных требований непрерывности частных производных по всем

своим аргументам (что, кстати, довольно часто не выполняется,

даже для простых задач) может быть найдено оптимальное

управление в форме синтеза.

Контрольные вопросы

1. В каком виде ищется оптимальное решение в задачах син-

теза оптимального управления ?

2. В чем заключаются достоинства практического использова-

ния управления в виде синтеза ?

3. В чем состоят трудности нахождения оптимального решения

в форме синтеза управления ?

4. Каким образом найти оптимальное управление в форме

синтеза, если изменение состояния динамической системы опи-

сывается

линейными дифференциальными уравнениями, а

функционал является квадратичным ?

5. В чем состоит суть принципа оптимальности ?

6. В чем заключаются основные особенности поиска опти-

мального решения с использованием алгоритма динамического

программирования ?

220

11. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ОПТИМАЛЬНОГО

УПРАВЛЕНИЯ

11.1. Оптимальное управление сближением КА

В 8.4.1. рассматривалась постановка задачи оптимального

управления сближением КА. Первым вопросом, который возника-

ет при формализации задачи принятия решения с использовани-

ем динамических моделей, является определение понятия со-

стояния динамической системы. В зависимости от того, какой со-

став характеристик выбран в качестве состояния, определяется

вид дифференциальных уравнений, описывающих изменение

данного состояния во

времени. Так в 8.4.1 состояние описыва-

лось вектором x(t), состоящим из двух компонент x(t) =

║x

(t)

(t)║

= ║r(t) v(t)║

, где r(t) - скалярная функция времени, описы-

вающая изменение относительной дальности между КА; v(t) -

функция, описывающая изменение относительной скорости. В

этом случае дифференциальные уравнения, описывающие изме-

нение состояния, имеют вид

x x

2 1



u x



Отметим, что, если бы в качестве состояния были выбраны па-

раметры положения КА и его скорости в абсолютной геоцентри-

ческой системе координат (ортогональная система, центр которой

соответствует центру Земли), то движение того же самого объек-

та описывалось бы шестью дифференциальными уравнениями.

Величина прикладываемого импульса u(t) в любой момент

времени ограничивается техническими

характеристиками двига-

тельной установки

u(t) ∈ [-U

,+U

] .