Москвин Б.В. Теория принятия решений
Подождите немного. Документ загружается.

201
лыми, и значения d(α
1
) дифференцируемыми в окрестности α
o
,
для i-ой компоненты d
i
(α
1
) можно записать
d
i
(α
1
) = d
i
(α
о
) + ∇
т
d
i
(α
о
) (α
1
- α
о
) ,
или с учетом (9.10)
d
i
(α
1
) = d
i
(α
о
) + ∇
т
d
i
(α
о
) δ
о
, (9.11)
Здесь
∇
т
d
i
(α
о
) - транспонированный вектор градиента невязки d
i
по компонентам
α
() () () ()
т
о
n
i
о
2
i
о
1
i
о
i
т
d
,...,
d
,
d
d
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
α
α∂
∂
α
α∂
∂
α
α∂
∂
=α∇
Иначе (9.11) можно переписать
() () ()
n,...,1i,
d
dd
o
j
o
n
1j
j
i
o
i
1
i
=δα
α∂
∂
+α=α
∑
=
. (9.12)
В целом, исходя из (9.11), вектор невязок определяется как
d(
α
1
) = d(α
о
) + D(α
о
) δ
о
, (9.13)
где D(
α
о
) - матрица Якоби, вычисленная в α
о
,
() ()
o
j
i
o
d
D α
α∂
∂
=α
Значения
α
о
следует выбирать таким образом, чтобы невязки
d(
α
1
) в (9.13) свести к нулю. Тогда
δ
о
= -D
-1
(α
о
) d(α
о
). (9.14)
В целом схема итерационного процесса в соответствии с
методом Ньютона с учетом (9.10), 2(14) будет иметь вид
δ
k
= -D
-1
(α
k
) d(α
k
),
k = 0,1,.... (9.15)
α
k+1
= α
k
+δ
k
,
На каждой итерации производится вычисление матрицы
D(
α
k
), для чего необходимо решать (n+1) задачу Коши для сис-
темы 2n уравнений (9.2), (9.5). При этом используются прибли-
женные конечно-разностные формулы вида
()
(
)
(
)
j
k
n
k
j
k
1i
k
nj
k
j
k
1i
k
j
i
,...,,...,d,...,,...,d
d
σ
ααα−ασ+αα
≈α
α∂
∂
202
В соответствии с последней формулой один раз рассчиты-
ваются невязки d(
α
k
), i=1,...,n, при этом решается задача Коши
для 2n дифференциальных уравнений. Затем решается n задач
Коши, в которых придается поочередно приращение
σ
j
всем
компонентам
α
k
j
j=1,...,n.
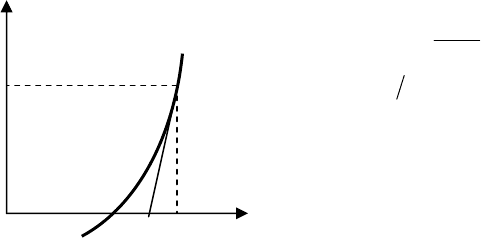
Метод Ньютона, предназначенный для поиска корней
функции, часто называют методом касательных. Действительно,
рассмотрим одномерный случай поиска корня функции d(
α), то-
гда ситуацию можно характеризовать следующим рисунком
d
d(
α
o
)
() ()
(
)
()()
() ()
..........................
dD
dd
d
dD
11
oo1
ooo
0
o
oo
α=α
δ+α=α
αα−=δ
δ
α
=α=α
α
1
α
o
α
В случаях, когда начальное приближение
α
о
выбирается
достаточно близко к корню функции, метод Ньютона сходится
достаточно быстро. Вместе с тем, при произвольном выборе
α
о
метод Ньютона может расходиться, что является его существен-
ным недостатком.
Существует большое число модификаций метода Ньютона,
позволяющих преодолеть указанный недостаток. В частности, из
выражения (9.15) следует, что
α
1
= α
о
+ δ
о
,
тогда, если
║d(α
1
)║ ≥ ║d(α
о
)║, (9.16)
то следует уменьшить поправку
δ
о
(обычно δ
о
домножают на β ∈
(0, 1)). При новом значении
α
1
= α
о
+ βδ
о
проверяют выполнение
условия (9.16) и, если оно выполняется , то производится даль-
нейшее уменьшение
β (как правило, β = 1/2, 1/4, 1/8,...). Подобная
модификация метода не гарантирует его сходимости, но расши-
ряет область применения метода.
203
Алгоритм Ньютона
0). Исходное состояние. Задается начальное приближение
значений сопряженных переменных
α
о
; критерий окончания про-
цесса
ε; номер шага k = 0.
1). Решается задача Коши для системы 2n дифференциаль-
ных уравнений вида (9.2), (9.5) при начальных условиях (x
o
,α
о
). На
каждом шаге численного интегрирования управление u(t) нахо-
дится из условия максимизации функции Гамильтона в соответ-
ствии с условием
()
(
)
) u, ,x t, (H max u*, ,x t, H
u
Gu
ψ
=
ψ
∈
, ∀t∈(t
o
,t
f
] .
2). Вычисляется d(
α
k
) = x(t
f
,α
k
) - x
f
.
Если
║d(α
k
)║ ≤ ε, то процесс счета окончен.
Если
║d(α
k
)║ > ε, то производится переход на шаг 3.
3). Решается n задач Коши, аналогично задаче п.1, но при на-
чальных условиях
α
k
(σ
j
), j=1,...,n. Здесь α
k
(σ
j
) - вектор, компоненты
которого определяются по правилу
()
⎪
⎩
⎪
⎨
⎧
=σ+α
≠α
=σα
ji,
ji,
j
k
i
k
i
j
k
i
В результате получаем n значений векторов невязок
d(
α
k
(σ
j
)) = x(t
f
, α
k
(σ
j
)) - x
f
, j = 1,...,n.
4). Строится матрица D(
α
k
)
()
(
)
(
)
(
)
j
k
ij
k
i
k
dd
D
σ
α−σα
=α
5). Производится вычисление поправки
δ
k
и нового значения
вектора сопряженных переменных
α
k+1
δ
k
= -D
-1
(α
k
) d(α
k
),
α
k+1
= α
k
+δ
k
,
6). k = k+1. Переход на шаг 1.
Описанный алгоритм Ньютона широко используется при
решении разнообразных задач оптимального управления. Основ-
ные трудности его использования связаны, как отмечалось, с не-
определенностью задания начального приближения сопряженных
переменных
α
о
. Другие трудности использования рассмотренного
204
алгоритма Ньютона связаны с низкой устойчивостью решения,
которая проявляется при больших интервалах управления (t
o
,t
f
].
В этом случае незначительные изменения начальных значений
сопряженных переменных
α могут вызывать значительные из-
менения решения x(t
f
,α). По этим причинам метод Ньютона, не-
смотря на его простоту и удобство описания, не стал универсаль-
ным методом расчета оптимальных управлений на основе реше-
ния краевых задач.
В этой связи стали развиваться другие способы решения
краевых задач, в частности, методы переноса граничных условий,
методы, использующие процедуры решения задач со свободным
правым концом [52, 53, 63].
9.4. Алгоритм И.Крылова-Ф.Черноусько
Метод, предложенный И.А. Крыловым и Ф.Л. Черноусько в
1962 году [53], первоначально использовался для решения задач
оптимального управления со свободным правым концом. В то же
время, вводя в функционал терминальный член, штрафующий
отклонение фазовых переменных в финальный момент времени
от заданных значений, данный метод может быть распространен
на рассматриваемые задачи
с фиксированными концами.
Основная идея метода состоит в том, что задается (каким
либо образом) некоторое д и с п е т ч е р с к о е управление
u
о
(t). Тогда при известных начальном состоянии x
o
и управлении
u
о
(t) можно вычислить (решая задачу Коши) состояние системы в
финальный момент времени, которое зависит от диспетчерского
управления, x(t
f
,u
о
). Такое состояние может не совпадать с задан-
ным состоянием x
f
, но можно вычислить значение сопряженных
переменных в финальный момент
ψ(t
f
). Тогда, интегрируя сопря-
женную систему дифференциальных уравнений в о б р а т н о м
времени, можно получить значение сопряженных переменных в
начальный момент времени
ψ(t
o
). Теперь на левом конце траек-
тории имеются начальные условия для фазовых и сопряженных
переменных x(t
o
) и ψ(t
o
). Тогда, интегрируя основную и сопря-
женную систему дифференциальных уравнений в прямом време-
ни, и вычисляя управляющие воздействия, исходя из максимиза-
ции функции Гамильтона, находится новое управление u
1
(t), ко-
торое заменяет диспетчерское. Процедура продолжается до тех
пор, пока
║x(t
f
,u
k
) - x
f
║ > ε, k=0,1,2,…
Рассмотрим соответствующий алгоритм.

205
Алгоритм
.
0). Исходное состояние. На основе анализа исходной задачи
задается диспетчерское управление u
о
(t); критерий окончания
процесса
ε; номер шага k = 0;
1). Решается задача Коши для системы n дифференциальных
уравнений (9.2)
x
(t) = ϕ ( t, x, u
k
), t∈(t
o
, t
f
]
при известных начальных условиях x(t
o
) = x
o
и диспетчерском
управлении u
k
(t). В результате находим состояние системы в фи-
нальный момент времени x(t
f
,u
k
).
2). Рассчитываются значения сопряженных переменных в фи-
нальный момент времени по формулам
()
(
)
(
)
,n,...,1,0i,
x
xu,tx
St
i
2
fi
k
fi
ifi
=
∂
−∂
−=ψ (9.17)
где S
i
- константа, характеризующая размер штрафа за наруше-
ние i-го краевого условия.
3). Производится интегрирование сопряженной системы диф-
ференциальных уравнений в обратном направлении времени (от
момента t
f
к моменту времени t
o
)
ψ
(t) = ξ( t, ψ), t∈(t
f
, t
o
]
при начальных условиях
ψ(t
f
). В результате получается траекто-
рия изменения сопряженных переменных, и в момент времени t
o
вычисляется значение
ψ(t
o
).
4). При известных начальных условиях x(t
o
), ψ(t
o
) решается
система 2n дифференциальных уравнений
x
(t) = ϕ ( t, x, u
k
), t∈(t
o
, t
f
]
ψ
(t) = ξ( t, ψ), t∈(t
o
, t
f
]
На каждом шаге ищется управление u
k+1
(t), исходя из условия
максимизации функции Гамильтона

206
). v, ,x (t, H max ),u ,x (t, H
u
Gv
1k
ψ=ψ
∈
+
5). Проверяется критерий окончания итерационного процесса:
если
║x (t
f
, u
k+1
) - x
f
║ ≤ ε, то процесс заканчивается,
если
║x (t
f
, u
k+1
) - x
f
║ > ε, тогда k = k+1, и производится переход на
шаг 2.
Рассмотренный алгоритм показал достаточную эффектив-
ность при решении ряда задач оптимального управления косми-
ческими средствами. Вместе с тем в ряде случаев он может рас-
ходиться. В этой связи был предложен ряд способов улучшения
сходимости. В частности, один из этих способов заключается в
том, что
на k-ой итерации новое приближение управления u
k+1
,
которое вычисляется в соответствии с п.4, реализуется не на
всем интервале (t
o
, t
f
], а лишь на его части (t
k
, t
f
], где t
k
∈(t
o
, t
f
].
Тогда на k-ой итерации управление u
k+1
(t) имеет вид
()
⎪
⎩
⎪
⎨
⎧
∈
∈
=
+
+
]t,t(t,)t(u
]t,t(t,)t(u
tu
f
k1k
k
o
k
1k
Здесь u
k
(t) - управление предыдущего шага,
u
k+1
(t) - управление, вычисляемое в соответствии с п.4 ал-
горитма.
Действительно, если t
k
= t
f
, то управление, а, соответствен-
но, и значение функционала на k-ой и (k+1)-ой итерации совпа-
дают. С другой стороны, если t
k
=t
o
, то естественно ожидать наи-
большего прироста функционала. Таким образом, параметр t
k
может служить для регулирования сходимости алгоритма и выби-
рается с тем, чтобы обеспечивалось уменьшение функционала
на k-ой итерации.
9.5. Особые (вырожденные) и скользящие режимы
управления
Для поиска оптимального управления на основе принципа
максимума (см. (9.7)) необходимо в каждый момент времени ре-
шать задачу нелинейного программирования вида
). u, ,x (t, H max arg (t)*u
u
Gu
ψ
=
∈

207
В ситуациях, когда множество допустимых управлений G
u
выпукло, замкнуто и ограничено, а функция Гамильтона вогнута,
решение такой задачи нелинейного программирования при фик-
сированных t, x,
ψ существует и единственно. В этом случае
управление u*(t) удовлетворяет необходимым условиям сущест-
вования оптимального управления и является экстремалью.
Вместе с тем при решении задачи максимизации функции
Гамильтона по множеству допустимых управлений G
u
возможны
ситуации, когда
а) на некотором интервале времени (t
1
,t
2
], t
1
,t
2
∈(t
о
, t
f
] функция
Гамильтона не зависит от управления u;
б) на некотором интервале времени (t
3
,t
4
], t
3
,t
4
∈(t
о
,t
f
] опти-
мальное управление не единственно, т.е. существует несколько
управлений u*(t), доставляющих максимум функции Гамильтона.
Первая группа ситуаций приводит к так называемым осо-
бым [38,52] или вырожденным [5] режимам управления, вторая
группа ситуаций - к скользящим [52] режимам управления. Пояс-
ним кратко особенности указанных режимов.
Особый режим управления.
Итак, пусть на некотором интервале времени (t
1
,t
2
], t
1
,t
2
∈
(t
о
,t
f
] гамильтониан H(t,x,u,ψ), t∈(t
1
,t
2
] не является функцией
управления (не зависит от u), тогда
()
0
u
,u,x,t
=
∂
ψΗ∂
. (9.18)
В этом случае интервал времени (t
1
,t
2
] называется участком
о с о б о г о (в ы р о ж д е н н о г о [5]) режима управления;
управление u(t), t
∈(t
1
,t
2
] называется о с о б ы м управлением.
Так как в соответствии (9.18) на участке особого управле-
ния частная производная функции Гамильтона по управлению,
как функция времени, тождественно равна нулю, то функция u(t)
и функции x(t),
ψ(t) могут на этом участке принимать только такие
значения, что
1,2,...k 0,
u
dt
d
k
k
==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
Η∂
... (9.19)
Последнее выражение совместно с (9.18) позволяет выде-
лить все участки особого режима.

208
Необходимое условие оптимальности особого управления
при решении задачи на минимум функционала будет иметь вид
[38]:
0
u
td
d
u
2
2
≥
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
Η∂
∂
∂
(9.20)
Если же решается задача максимизации функционала, то знак
неравенства в (9.20) меняется на противоположный.
В соответствии с (9.20) может выделяться некоторое мно-
жество особых управлений. Таким образом, существование осо-
бого режима приводит к тому, что задача оптимального управле-
ния при некоторых начальных условиях имеет множество опти-
мальных управлений.
Оптимальное в целом управление
находится таким обра-
зом, что на обычных участках оно выбирается в соответствии с
принципом максимума, а на особых участках выбирается одно из
управлений, удовлетворяющих (9.20).
Скользящий режим управления.
В ситуациях, когда на некотором интервале времени (t
3
, t
4
],
t
3
,t
4
∈ (t
o
,t
f
] оптимальное управление не единственно, т.е. сущест-
вует несколько различных управлений u*
0
(t), u*
1
(t) ,..., u*
k
(t), дос-
тавляющих максимум гамильтониану в момент t. Такие ситуации
могут складываться либо, если функция Гамильтона многоэкс-
тремальна, либо, если множество допустимых управлений G
u
не-
выпукло. Такие ситуации приводят к, так называемым, с к о л ь -
з я щ и м режимам управления [38,52].
Проблема выбора оптимального управления при t∈(t
3
, t
4
]
заключается в том, что в соответствии с каждым, прикладывае-
мым к системе, управлением u*
j
(t), j=0,...,k изменяется и состоя-
ние динамической системы
), * u x,t, ( (t) x
j
ϕ=
причем в каждый момент времени можно выбирать любое из
u*
j
(t), j=0,...,k управлений. При этом на интервале времени t∈(t
3
,
t
4
] можно строить различные последовательности управлений
(а, следовательно, и фазовые траектории).
Разобьем промежуток (t
3
, t
4
] на s частей точками τ
p
, p=0, ..
.., s таких, что t
3
= τ
o
<τ
1
<....<τ
s
= t
4
. Причем выполняется условие
при
1.-s0,...,p 0, max s
p1p
p
s
=→τ−τ=δ∞→
+
209
Каждая точка x
s
(τ
p
) соединяется с точкой x
s
(τ
p+1
) ломаной лини-
ей, составленной из отрезков
ϕ (t, x(τ
p
), u*
j
(τ
p
))⋅t , j=0,...,k.
Построенная таким образом ломаная x
s
(t) является решением
уравнений состояния. В целом же последовательность {x
s
(t), u
s
(t)}
удовлетворяет дифференциальным связям, доставляет минимум
функционалу, и является минимизирующей последовательно-
стью, которая при s─>∞ стремится к оптимальному скользящему
режиму.
Особенности реализации алгоритмов, позволяющих выяв-
лять оптимальные скользящие режимы, рассмотрены в [52].
Контрольные вопросы
1. Какие различаются методы решения задач оптимального
управления?
2. Какие методы решения задач оптимального управления
строятся на основе использования принципа максимума
Л.С.Понтрягина ?
3. В чем состоит суть краевой задачи, и в чем заключаются
трудности ее решения ?
4. Каким образом обеспечивается решение краевой задачи на
основе метода Ньютона? В чем его достоинства
и недостатки ?
5. В чем заключаются особенности решения краевой задачи на
основе метода Крылова-Черноусько? В чем достоинства и недос-
татки метода ?
6. В результате чего появляются вырожденные управления?
Каким образом принимать решение в этом случае ?
7. В результате чего появляются скользящие режимы управ-
ления ?
210
10. АЛГОРИТМЫ ВЫБОРА ОПТИМАЛЬНОГО РЕШЕНИЯ
В ФОРМЕ СИНТЕЗА УПРАВЛЕНИЯ
10.1. Постановка задачи синтеза управления
Рассмотренные в предыдущем разделе методы и алгорит-
мы позволяют найти оптимальное управление в форме некоторой
функции от времени u(t), такое управление называют программ-
ным управлением и оно позволяет перевести динамическую сис-
тему из заданного начального состояния в конечное состояние с
некоторым наилучшим качеством, задаваемым функционалом.
Вместе с тем в ряде приложений
целесообразно находить управ-
ление, не привязанное к конкретному начальному состоянию, но
являющееся функцией от состояния u(t,x(t)) или функцией от вы-
хода u(t,y(t)), т.е. в форме с и н т е з а управления или в форме
управления с о б р а т н о й с в я з ь ю
.
Разработка вычислительных методов синтеза представля-
ется весьма перспективным направлением развития управления
современными автоматизированными системами. Реализация
управления в форме синтеза позволяет более успешно решать
целевые задачи в условиях неопределенности обстановки, по-
вышать устойчивость управления. Это связано, прежде всего, с
тем, что реальные условия функционирования системы могут от-
личаться от тех, которые
были учтены в математической модели,
использованной при поиске оптимального программного управле-
ния. Тогда реальное состояние системы в момент t может быть
отлично состояния, рассчитанного на модели, а, следовательно,
и управление, найденное как функция времени, не отвечает сло-
жившимся (или изменившимся) условиям. В отличие от про-
граммного управления оптимальное управление u*(t,x(t)), рассчи-
танное в
форме синтеза, в каждый момент времени t зависит
