Москвин Б.В. Теория принятия решений

Подождите немного. Документ загружается.

181

Цель проводимой операции - сближение космических аппа-

ратов, следовательно, их можно рассматривать, как систему, со-

стоящую из двух материальных точек, перемещающихся в про-

странстве. Состояние такой системы можно описать векторной

функцией времени x(t) =

║x

(t) x

(t)║

, где x

(t) =r(t) - скалярная

функция времени, описывающая изменение относительной даль-

ности между КА; x

(t) = v(t) - функция, описывающая изменение

относительной скорости. Тогда дифференциальные связи компо-

нент вектора состояния x(t) описываются уравнением

(t) r d

= u(t) ,

т.е. в соответствии со вторым законом Ньютона, ускорение равно

прикладываемому импульсу. Иначе последнее уравнение можно

переписать в виде системы двух дифференциальных уравнений

(t) = x

(t) .

(t) = u(t) .

Прикладываемый импульс ограничивается техническими

характеристиками двигательной установки, тогда

u(t) ∈ [-U

,+U

]

Начальное состояние системы соответствует некоторому

положению КА в пространстве, тогда

x(t

) = ║r(t

) v(t

)║

= ║r

║

Конечное состояние соответствует сближению КА, тогда

x(t

) = ║ 0 0 ║

Произвести сближение следует за минимальное время, то-

гда функционал, описывающий качество управления имеет вид

∫

dt → min.

Рассматриваемая задача является задачей оптимального

управления с функционалом Лагранжа с фиксированными конца-

ми и свободным временем. Пусть t

= 0, t

= Т, тогда задачу можно

представить в виде

182

1. Функционал

∫

dt → min.

2. Дифференциальные связи



= x



= u .

3. Ограничения вдоль траектории

u(t) ∈ [-U

,+U

] или ⎮u (t)⎮ ≤ U

, t∈(0,T] .

4. Краевые условия

x(0) =

║r

║

; x(T) = ║ 0 0 ║

8.4.2. Управление операциями обслуживания

космического аппарата.

Для обеспечения целевого функционирования КА необхо-

димо проводить ряд операций (работ), связанных с анализом со-

стояния и управлением движения КА, связанных с анализом тех-

нического состояния и управлением бортовой аппаратурой. Такие

операции проводятся с использованием наземных средств

управления, расположенных на пунктах управления, в моменты

времени, когда КА попадает в зону

видимости того или иного

пункта. В этих условиях необходимо найти программу управления

выполнения операций обслуживания, позволяющую минимизиро-

вать расход ресурсов.

Целью управления является выполнение операций обслу-

живания, поэтому в качестве состояния системы x(t) целесооб-

разно выбрать состояние операций x(t) =

║x

(t), x

(t) ,…, x

(t)║

где x

(t) - состояние i-ой операции обслуживания в момент вре-

мени t. Изменение состояния операций определяется диффе-

ренциальными уравнениями вида



= ε(t) d

u(t) ,

где

ε(t) - заданная функция, принимающая значение 1 в моменты

времени, когда КА попадает в зону видимости того или иного

пункта (операции обслуживания могут выполняться), и 0 в про-

тивном случае;

183

d = ║d

, d

,…, d

║

- вектор, характеризующий максимально

возможную интенсивность выполнения операций;

u(t) - векторная функция времени, характеризующая управле-

ние выполнением операций обслуживания.

Начальное состояние операций x(0) = 0; конечное состоя-

ние x(T), характеризующее факт выполнения операций, задано

как x(T) = x

зад

Необходимо найти программу выполнения операций об-

служивания, минимизирующую расход ресурсов тогда функцио-

нал, описывающий качество управления имеет вид

∫

(t) R(t) u(t)dt → min.

где R(t) - положительно определенная симметрическая матрица,

характеризующая расходование ресурсов в момент времени t.

Тогда задача оптимального управления в целом имеет вид

1. Функционал

∫

(t) R(t) u(t)dt → min.

2. Дифференциальные связи



ε(t) d

u(t) ,

3. Ограничения вдоль траектории: u(t)

∈ [0, 1]; x(t) ≤ x

зад

4. Краевые условия: x(0) = 0; x(T) = x

зад

8.5. Качественный анализ проблемы оптимального

управления

Поставленная задача оптимального управления динамиче-

ской системой может быть решена с использованием некоторого

алгоритма, но только в том случае, если решение (управление)

такой задачи существует. Исследование принципиальной разре-

шимости задачи оптимального управления, доказательство суще-

ствования и единственности решения и является предметом ка-

чественного анализа. Следует отметить, что существование оп-

тимального

управления в динамической системе (модели) не вы-

текает непосредственно из факта наличия управления в реаль-

ной системе. Последнее связано с тем обстоятельством, что по-

184

иск оптимального управления производится в рамках некоторого

математического формализма - модели, которая является агре-

гированным (обобщенным) представлением исходной ситуации, и

адекватность разработанной абстрактной модели исходной ре-

альной ситуации и определяет существование решения в задаче

оптимального управления.

Качественный анализ проблемы оптимального управления

включает три основные группы вопросов.

1. Исследование принципиальной возможности перевода ди-

намической системы из одного заданного состояния в другое за

конечное время с использованием некоторого программного

управления, принадлежащего заданному классу функций (управ-

ляемость динамической системы).

2. Анализ существования допустимого управления - управле-

ния, принадлежащего заданному классу функций, удовлетво-

ряющего заданным ограничениям и переводящего динамическую

систему из заданного начального состояния в заданное конечное

состояние (

достижимость состояний).

3. Анализ существования в классе допустимых управлений оп-

тимального управления и его единственность.

8.5.1. Управляемость динамической системы.

Динамическая система x



(t) = ϕ (x, u) называется у п р а в-

л я е м о й [5, 43] в состоянии x

=x(t

) относительно состояния

=x(t

), если существует кусочно-непрерывное управление u(t),

∈(t

], позволяющее перевести систему из состояния x

в со-

стояние x

Если существует кусочно-непрерывное управление, позво-

ляющее перевести динамическую систему из любого заданного

состояния в любое желаемое состояние за конечное время, то

система называется в п о л н е (полностью) управляемой.

Для линейных стационарных систем (8.5), описываемых n

дифференциальными уравнениями вида



(t) = Ax + Bu,

критерием полной управляемости является то, что ранг матрицы

G =

║B ¦ AB ¦ A

B ¦ … ¦ A

n-1

B║ равен n, т.е.

rang║B ¦ AB ¦ A

B ¦ … ¦ A

n-1

B║ = n . (8.33)

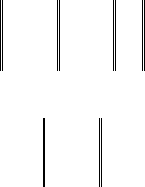
Например, в задаче 1.4.1 оптимального управления сближением

КА динамическая система описывается уравнениями

185

0 1 0



(t) = Ax + Bu =

x + u ,

0 0 1

тогда критерий управляемости

0 1

rang ║B ¦ AB║ = rang

= 2 .

1 0

Таким образом, система вполне управляема.

Анализ управляемости нелинейных динамических систем

достаточно сложен и здесь к настоящему времени получены

весьма немногочисленные результаты.

Интересен подход [17] к анализу необходимых условий

управляемости на основе исследования влияния управления на

компоненты вектора состояния, которое описывается ориентиро-

ванным графом. Действительно, так как управляемость это спо-

собность управления переводить

систему из одного произвольно-

го состояния в другое, то, очевидно, что если управление оказы-

вает влияние на изменение всех компонент вектора состояния

(прямое, или косвенное через другие компоненты), то система

управляема. В ориентированном графе Г = (W,E) множество

вершин W соответствует объединению W = X

∪ U, где X - мно-

жество компонент вектора состояния X; U - множество компо-

нент вектора управления; E

⊆ W×W - множество дуг, связываю-

щих вершины из W, причем входные вершины соответствуют

компонентам вектора состояния, стоящим в левой части диффе-

ренциальных уравнений, описывающих систему, а выходные

вершины соответствуют компонентам вектора состояния и управ-

ления, стоящим в правой части дифференциальных уравнений.

Для управляемости системы необходимо, чтобы все вершины X

были достижимы (существовал путь) из

вершин U.

В частности, в задаче 8.4.1 оптимального управления

сближением КА множество вершин W = {x

, x

, u}, множество дуг

E ={(x

),(u,x

)} и из вершины (u) существует путь в вершину x

это путь ((u,x

),(x

)), и существует путь в вершину x

- (u,x

8.5.2. Достижимость состояний динамической системы

Вопрос достижимости заданного состояния динамической

системы из некоторого начального состояния заключается в су-

ществовании допустимого управления - управления, принадле-

186

жащего заданному классу функций и удовлетворяющего задан-

ным ограничениям.

В реальных задачах краевые условия, описывающие тре-

буемое начальное и конечное состояние динамической системы,

могут быть заданы так, что в силу ограничений на возможные

управления (ограниченности ресурсов, например) система не в

состоянии достигать конечного состояния, т.е. не может быть ука-

зано

хотя бы одно допустимое управление. В этом случае реше-

ния задачи оптимального управления не существует. Действи-

тельно, в задаче 8.4.1 оптимального управления сближением КА

конечное состояние x(T) = (0,0) не может быть достигнуто из

произвольного начального состояния, если допустимые управле-

ния u(t) могут принимать только положительные значения, то

есть u(t)

∈[ 0, +U

], t∈(0,T].

Анализ достижимости состояний динамической системы, с

помощью которого оценивается выполнимость краевых условий,

требует решения довольно нетривиальной задачи - построения

областей достижимости или их аппроксимаций. В работах [39, 81]

приводятся теоремы и алгоритмы, используемые для построения

областей достижимости.

8.5.3. Существование и единственность оптималь-

ного управления

В задачах оптимального управления возможны случаи, ко-

гда при достижимости финального состояния динамической сис-

темы, т.е. в условиях существования допустимых управлений,

оптимального управления не существует. Такие ситуации могут

складываться, например, если функционал на множестве допус-

тимых управлений может неограниченно убывать (принимать

сколь угодно малые значения).

При качественном анализе процессов

управления динами-

ческими системами наряду с установлением факта существова-

ния оптимального управления целесообразно ставить вопрос о

его единственности. В настоящее время отсутствуют универсаль-

ные критерии для оценки единственности решения в задачах оп-

тимального управления динамическими системами, поэтому в

каждой конкретной задаче следует, исходя из её специфики, про-

водить индивидуальное исследование данного

вопроса.

187

8.6. Необходимые условия существования оптимального

управления

При проведении исследований задач оптимального управ-

ления динамическими системами важную роль играют необходи-

мые условия существования оптимального управления. Основное

содержание этих условий заключается в формулировании

свойств, присущих оптимальному управлению, т.е. свойств, кото-

рые имеют место, если оптимальное управление существует. С

другой стороны, если такие условия (необходимые) не выполня-

ются,

то и оптимального управления не существует. В связи с по-

следним положением необходимые условия довольно часто ис-

пользуются при качественном анализе существования оптималь-

ного управления. Однако прикладная роль этих условий значи-

тельно шире и помимо оценки качественных характеристик зада-

чи, они позволяют выявить множество экстремальных управле-

ний, т.е. подмножество допустимых

управлений, содержащее оп-

тимальное управление.

Исследование необходимых условий существования опти-

мального решения экстремальных задач, в которых решение опи-

сывается некоторой функцией, традиционно проводилось в рам-

ках вариационного исчисления, созданного трудами выдающихся

ученых прошлого таких, как Л.Эйлер, Ж.Лагранж, В.Гамильтон и

другие. В 1956 г. группой российских ученых под руководством

Л.С.Понтрягина были сформулированы в форме "принципа мак-

симума" необходимые условия оптимальности для задач, в кото-

рых учитываются важные для практических приложений ограни-

чения на возможные управления.

Принцип максимума существенно обобщает и развивает

результаты классического вариационного исчисления и, по суще-

ству, образует фундамент всей современной теории оптимально-

го управления. Именно

его появление стимулировало дальней-

шие исследования в области оптимального управления динами-

ческими системами при решении практически важных задач. В

результате проведения данных исследований произошла опре-

деленная стандартизация терминологии, методов и алгоритмов

оптимального управления.

Рассмотрим принцип максимума Понтрягина для некоторых

задач оптимального управления, при формулировании которого

существенно используется некоторая специальная функция -

функция Гамильтона.

188

8.6.1. Функция Гамильтона.

Изменение состояния x(t) = (x

(t),...,x

(t)) динамической сис-

темы под воздействием управления u(t) описывается дифферен-

циальными уравнениями (8.26)



(t) = ϕ ( t, x, u ),

Пусть необходимо найти такое управление u(t), чтобы дос-

тигался минимум функционала (8.29) (задача Лагранжа)

J(x,u) =

∫

F(t,x,u) dt

Значение функционала J(x,u) определяется, в первую очередь,

управлением, поэтому такое значение можно рассматривать, как

еще одну компоненту вектора состояния x

(t)=J(x,u). Тогда рас-

ширенный вектор состояния имеет (n+1) компоненту

x (t) = ( x

,…, x

)

. (8.34)

Его изменение под воздействием управления описывается

дифференциальными уравнениями

(t) xd

= ϕ

( t, x, u), i=0,…,n ,

Причем

(t,x,u) = F(t,x,u). (8.35)

Тогда вектор сопряженных переменных

ψ (t) = (ψ

(t), ψ

(t) ,…, ψ

(t))

имеет (n+1) компоненту и его изменение описывается системой

дифференциальных уравнений (8.21)

()

(

)

()

,n,...,0i,t

u,x,t

=ψ

∂

ϕ∂

−=

∑

(8.36)

Введем в рассмотрение ф у н к ц и ю Г а м и л ь т о н а, как

скалярное произведение

H(t,

x ,u,

) = (

, ϕ) = ϕ

ϕ =

∑

(t,x,u). (8.37)

С использованием функции Гамильтона основную и сопря-

женную систему дифференциальных уравнений можно перепи-

сать в виде

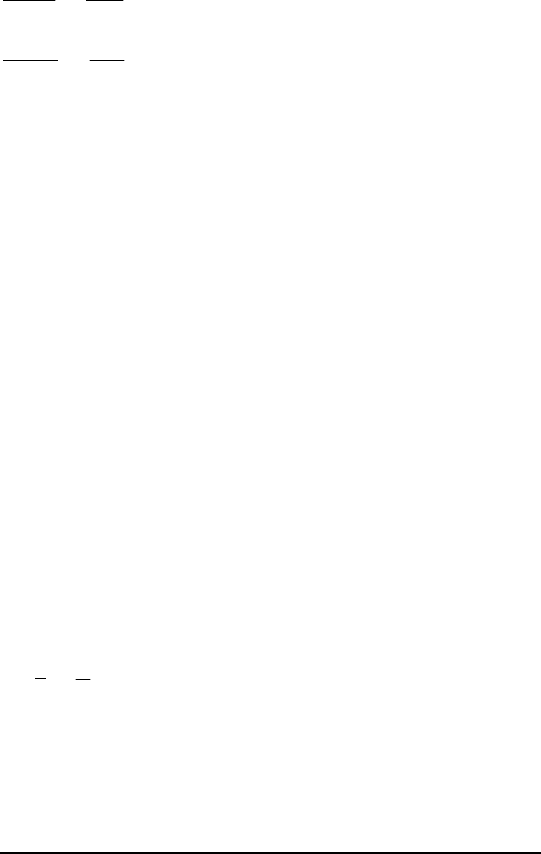
189

(t) xd

ψ∂

∂

, i = 0,…,n, (8.38)

(t) d

∂

, i = 0,…,n, (8.39)

Интегрируя основную и сопряженную системы дифферен-

циальных уравнений, при известных начальных условиях, можно

получать значения фазовых и сопряженных переменных в любой

момент времени.

8.6.2. Принцип максимума Л.С.Понтрягина.

Рассмотрим формулировку принципа максимума для зада-

чи поиска оптимального управления, переводящего динамиче-

скую систему из одного заданного состояния в другое заданное

состояние, при этом управление должно в любой момент времени

удовлетворять ограничениям и минимизировать некоторый функ-

ционал, отражающий интегральное качество управления. Такая

задача является задачей Лагранжа со свободным временем и

фиксированными концами.

J(x,u) =

∫

F(t,x,u) dt → min (8.40)



(t) = ϕ ( t, x, u ), (8.41)

u(t)

∈ G

⊆ R

, t∈(t

, t

] (8.42)

x(t

) = x

, x(t

) = x

. (8.43)

Функция Гамильтона для задачи (8.40) - (8.43) будет иметь

вид

H(t,

x ,u, ψ ) = ψ

F(t,x,u) + ψ

ϕ (t,x,u). (8.44)

Дифференциальные уравнения, описывающие изменение сопря-

женных переменных

ψ(t), имеют вид (8.36).

Необходимые условия оптимальности управления форму-

лируются в виде следующего утверждения.

Утверждение (Принцип максимума Л.С.Понтрягина).

Если управление u*(t) является оптимальным управлением

в задаче (8.40)-(8.43), то существует ненулевая непрерывная век-

торная функция (

(t),ψ

(t),...,ψ

(t)), удовлетворяющая сопряжен-

190

ной системе дифференциальных уравнений (8.36) и такая, что

выполняются условия

1). Для любого момента времени t

∈(t

] функция Гамильтона

(8.44) достигает максимума по u(t), т.е.

H(t,

x ,u*,

) = max H(t, x ,u,

). (8.45)

u∈G

2). Выполняются соотношения

) ≤ 0; H(t

, x ,u*,

) = 0. (8.46)

Замечание 1.

Условие 1 принципа максимума может служить основой для

вычисления оптимального управления на основе решения неко-

торой специализированной краевой задачи. Действительно, из-

менение фазовых переменных x(t) описывается дифференциаль-

ными уравнениями (8.41), изменение сопряженных переменных

ψ(t) описывается дифференциальными уравнениями (8.36), при

известных начальных условиях (x

, ψ

) фазовые и сопряженные

переменные для любого момента времени t можно вычислить. В

этом случае гамильтониан в (8.45), становится функцией одного

переменного u, которое может быть вычислено для момента

времени t при соблюдении ограничений u

∈G

Последовательно решая задачу Коши для (2n+2) диффе-

ренциальных уравнений (8.41), (8.36), описывающих изменение

фазовых и сопряженных переменных, для каждого момента вре-

мени t

∈(t

], и, находя оптимальное управление из условия мак-

симизации гамильтониана, можно найти оптимальную программу

управления u*(t) в целом. Такая задача называется к р а е в о й

задачей.

Основная особенность рассматриваемой здесь краевой за-

дачи заключается в том, что начальные условия для сопряжен-

ных переменных

ψ(t

) не заданы. Вместе с тем фазовая траек-

тория должна быть такова, чтобы x(t

)=x

, и в момент t

выполня-

лись соотношения (8.46).

Замечание 2.

Формулировки принципа максимума для различных задач

оптимального управления отличаются видом функции Гамильто-

на (т.к. могут использоваться разные функционалы) и условиями

2 в формулировке принципа максимума. Например, в рассмот-

ренной задаче Лагранжа (8.40)-(8.43), но с фиксированным вре-