Москвин Б.В. Теория принятия решений
Подождите немного. Документ загружается.


171
Переходная матрица свободной стационарной динамиче-
ской системы, описываемой однородными дифференциальными
уравнениями с постоянными коэффициентами (8.9),
(t)x
= A x
представляет собой экспоненту от At, т.е. (рассмотрим случай,
когда t
о
= 0)
Ф(t, t
о
) = Ф(t - t
о
) = Ф(t) = e
Аt
, (8.19)
где e
Аt
=
∑
∞
=0k
A
k
(t
k
/ t!) . (8.20)
Итак, если уравнения состояния являются нелинейными, то
состояние x(t), в которое перейдет система из некоторого началь-
ного состояния x(t
о
), рассчитывается на основе численных мето-
дов. Для линейной системы рассчитывается переходная матрица
Ф(t,t
о
), и состояние в момент t определяется как x(t) = Ф(t,t
о
) x(t
о
)
для любого начального состояния x(t
о
). В этой связи довольно
часто для удобства исследования систем производится ее ли-
неаризация, с заменой нелинейных уравнений состояния линей-
ными уравнениями. В настоящее время при исследовании дина-
мических систем наиболее широко используются два способа
линеаризации.
1-ый способ - пошаговая линеаризация. Весь интервал
управления (t
o
,t
f
] разбивается на интервалы (t
i
, t
i+1
], i = 0,.., N-1
меньшей длительности, и на каждом таком интервале система
описывается линейными дифференциальными уравнениями,для
которых находится переходная матрица Ф
i
(t,t
i
). Тогда состояние в
момент t можно определить как
x(t) = Ф
i
(t,t
i
) x(t
i
), t∈(t
i
, t
i+1
].
2-ой способ - линеаризация вблизи опорной траектории. В
этом случае x(t) = x
o
(t) + δx(t), где x
o
(t) - опорная траектория, δx(t)
- отклонение от опорной траектории. Аналогично, u(t) = u
o
(t) +
δu(t). Тогда нелинейную систему дифференциальных уравнений
(8.3) можно переписать
dt
d
(x
o
(t) + δx(t)) =
dt
xd
o
(t)
+
dt
(t)x d
δ
=
= ϕ ( t,x
o
,u
o
) + F
x
( t,x
o
,u
o
) δx(t) + F
u
( t,x
o
,u
o
) δu(t) + δF(t) .
Здесь F
x
(t,x
o
,u
o
) = ║∂ϕ
i
/∂x
j
║ - матрица Якоби по x; F
u
(t,x
o
,u
o
) =
║∂ϕ
i
/∂u
j
║ - матрица Якоби по u; δF(t) - остаточный член. Пренеб-
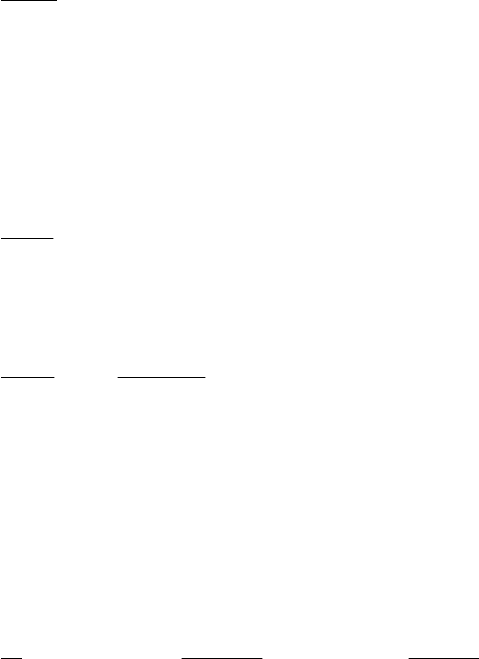
172
регая в последнем выражении остаточным членом δF(t), можно
записать дифференциальные уравнения для отклонений от
опорной траектории
dt
(t)x d
δ
= A
o
(t) δx(t) + B
o
(t) δu(t)) .
Матрицы A
o
(t) и B
o
(t) зависят от опорной траектории, соответст-
венно, и переходная матрица Ф
o
(t,t
о
) будет справедлива при про-
гнозе движения линеаризованной динамической системы вблизи
конкретной опорной траектории.
8.2.3. Сопряженная система
Наряду с системой дифференциальных уравнений (8.3)
dt
(t) xd
i
= ϕ
i
( t, x, u), i = 1,…,n ,
описывающих изменение состояния динамической системы, в
задачах оптимального управления часто рассматривают с о п -
р я ж е н н у ю систему дифференциальных уравнений
()
(
)
()
,n,...,1i,t
x
u,x,t
dt
td
j
n
1j
i
j
i
=ψ
∂
ϕ∂
−=
ψ
∑
=
(8.21)
Если исходная система дифференциальных уравнений ли-
нейная, т.е. имеет вид (8.8), то в соответствии с (8.21) сопряжен-
ная система имеет вид
ψ
(t) = - A
т
ψ. (8.22)
Система (8.22) представляет собой однородную систему диффе-
ренциальных уравнений, переходную матрицу этой системы обо-
значим как Ψ(t,t
o
). Аналогично (8.15), матрица Ψ(t,t
o
) является
решением системы (8.22). Тогда
()()
()
(
)
() ()
(
)
=
Φ
Ψ+Φ
Ψ
=ΦΨ
dt
t,td
t,tt,t
dt
t,td
t,tt,t
dt
d
о
о
т
о
о
т
оо
т
= ( - A
т
(t) Ψ(t,t
o
))
т
Ф(t,t
о
) + Ψ
т
(t,t
o
) A(t) Ф(t,t
о
) =
= - Ψ
т
(t,t
o
) A(t) Ф(t,t
о
) + Ψ
т
(t,t
o
) A(t) Ф(t,t
о
) = 0 .
Таким образом, Ψ
т
(t,t
o
) Ф(t,t
о
) = const, ∀t∈(t
o
,t
f
]. Но, поскольку в
момент t=t
o
, Ψ
т
(t
o
,t
o
) Ф(t
o
,t
о
) = E, то Ψ
т
(t,t
o
) Ф(t,t
о
) = E, ∀t∈(t
o
,t
f
].
Тогда
Ψ
т
(t,t
o
) = Ф
-1
(t,t
о
) = Ф(t
о
,t), ∀t ∈ (t
o
,t
f
]. (8.23)

173
Рассмотрим, как изменяется скалярное произведение век-
торов состояний прямой и сопряженной систем
() ()
()
(
)
()
()
=ψ+
ψ
=ψ
dt
tdx
t)t(x
dt
td
txt
dt
d
т
т
т
= ( - A
т
(t) ψ (t))
т
x(t) + ψ
т
(t) (A(t) x(t) + B(t) u(t)) =
= - ψ
т
(t) A(t) x(t) + ψ
т
(t) A(t) x(t) + ψ
т
(t) B(t) u(t) =
= ψ
т
(t) B(t) u(t).
Таким образом, в условиях отсутствия управления скаляр-
ное произведение векторов состояний прямой и сопряженной
систем постоянно.
8.3. Постановка задач оптимального управления
Принятие решения в военно-технических системах, когда
решение формализуется (математически описывается) векторной
функцией времени, основывается на методах, развитых в совре-
менной теории оптимального управления. Данная теория начала
интенсивно развиваться в конце сороковых, начале пятидесятых
годов ХХ столетия. Следует отметить, что побудительным толч-
ком активного проведения данных исследований явились, в пер-
вую очередь, потребности развивающейся ракетно-космической
теории и практики. После опубликования результатов работ, вы-
полненных школой Л.С.Понтрягина [75], произошла определенная
стандартизация терминологии и методики решения задач в рам-
ках новой научной дисциплины, которая получила название тео-
рии оптимального управления. В настоящее время данная идео-
логия глубоко проникла во все сферы
исследований и конструк-
торских разработок военно-технических систем. В этой связи в
данном пособии при изложении вопросов принятия решений на
динамических моделях будем придерживаться существующих
понятий и терминов.
Вместе с тем с целью рассмотрения на единой концепту-
альной основе задач принятия решений, использующих модели
различной природы, рассмотрим обобщенную модель выбора
(см. 1.4), которая может быть представлена как
( Q(s), Δ, { r
i
, i∈C}, f) . (8.24)
174
Здесь
Q(s) - исходная структура выбора (модель) типа s. Данная
структура позволяет ставить задачи выбора, связанные с теми
или иными структурными (модельными) ограничениями, зада-
ваемыми посредством, например, дифференциальных уравнений
для динамических систем или посредством сетей, алгебраиче-
ских уравнений для статических систем.
Δ - пространство альтернатив (решений). В зависимости от
типа исходной структуры выбора Q(s) это
некоторое конечно-
мерное пространство векторов или пространство векторных
функций, отдельный элемент которого характеризует структуру
решения (альтернативы), состав и смысл компонент этой альтер-
нативы.
{r
i
, i∈С} - множество отношений, ограничивающих выбор; С -
множество индексов отношений, ограничивающих выбор. Данные
отношения задаются на Δ и вводятся непосредственно при по-
становке задач выбора, они отражают основные ограничения,
связанные с процессом функционирования рассматриваемых
систем.
f - отношение предпочтения, задаваемое на множестве
альтернатив Δ и отражающее требования, предъявляемые к оп-
тимальному решению.
Для рассматриваемых здесь задач оптимального управле-
ния исходная структура выбора Q(s) задается системой диффе-
ренциальных уравнений
(t)x
= ϕ ( t, x, u ),
Пространство альтернатив Δ представляет собой декартово
произведение базовых множеств Δ = T×X×U, где T - множество
моментов времени; X - множество состояний системы; U - множе-
ство управлений.
Множество отношений, ограничивающих выбор, {r
i
, i ∈ С}
задает на Δ множество допустимых альтернатив G =G
t
×G
x
×G
u
⊆Δ.
Отношение предпочтения f , как правило, задается с ис-
пользованием функций (целевых функций, функционалов) вида
f: Δ → R
1
или f: T×X×U → R
1
.
Таким образом, элементами Δ является тройки вида (t,x,u).
На самом деле выбирается пара функций (x(t),u(t)), причем в
соответствии со структурой выбора, которая задается системой
дифференциальных уравнений и, в силу теоремы существования
175
и единственности, программа управления u(t) при заданном x(t
о
)
однозначно определяет фазовую траекторию x(t), ∀t∈T, т.е. ис-
комое решение однозначно определяется функцией u(t). Следо-
вательно, ограничения в задачах оптимального управления могут
задаваться на T×X×U, а решением данной задачи является про-
грамма управления u(t). В этих условиях отображение f: T×X×U
→ R
1
представляет собой функционал J(t,x,u) или J(x(t),u(t)),
действующий из пространства функций (состояния и управления)
в множество действительных чисел, и, в соответствии со сло-
жившейся в теории оптимального управления практикой, ищется
м и н и м у м этого функционала.
Тогда, в достаточно общем виде, задача оптимального
управления может быть сформулирована следующим образом.
Необходимо
найти векторную функцию управления u(t),
t∈T, доставляющую минимум функционалу
J(x,u) → min (8.25)
при управлении динамической системой
(t)x
= ϕ ( t, x, u ), (8.26)
которое удовлетворяет ограничениям вдоль траектории
(t,x,u) ∈ G = G
t
×G
x
×G
u
⊆ Δ=R
1
×R
n
×R
m
, (8.27)
при переводе системы из начального состояния x(t
o
) в конечное
состояние x(t
f
)
x(t
o
) ∈ E
о
⊆ R
n
,
x (t
f
) ∈ E
f
⊆ R
n
. (8.28)
Итак, в постановке задачи оптимального управления при-
сутствует четыре элемента.
1). Функционал: J ( x, u) → min .
2). Дифференциальные связи (динамическая система):
(t)x
= ϕ ( t, x, u ) .
3). Ограничения вдоль траектории: (t,x,u) ∈ G = G
t
×G
x
×G
u
.
4). Краевые условия: x(t
o
) ∈ E
o
, x(t
f
) ∈ E
f
.
Конкретизация указанных четырех элементов порождает
различные типы задач. Рассмотрим варианты задания указанных
элементов постановки задачи оптимального управления.

176
8.3.1. Способы задания функционала.
В зависимости от способа задания различают несколько
видов функционалов, а, соответственно, задач оптимального
управления:
З а д а ч а Л а г р а н ж а (интегральный функционал), ка-
чество управления характеризуется некоторыми интегральными
на всем интервале управления характеристиками, тогда функ-
ционал имеет вид
J(x,u) =
∫
f
t
t
0
F(t,x,u) dt → min (8.29)
где F - некоторая дифференцируемая функция своих аргумен-
тов. Простейшим видом задачи Лагранжа является задача, в ко-
торой F(t,x,u) = 1. Тогда
J(x,u) = t
f
- to → min,
т.е. задача становится задачей м а к с и м а л ь н о г о б ы с т -
р о д е й с т в и я.
З а д а ч а М а й е р а (терминальный функционал), каче-
ство управления
определяется значением фазовых переменных,
которые достигаются на концах траектории.
J(x,u) = Ф( t
o
, x(t
o
), t
f
, x(t
f
)) → min . (8.30)
Например, функционал данного вида может характеризовать сте-
пень приближения конечного состояния динамической системы к
заданному состоянию x
зад
(t
f
). Тогда
J(x,u) = Ф( t
f
, x(t
f
)) = (x
зад
(t
f
) - x(t
f
))
2
→ min.
Формально задачу Лагранжа можно представить в виде за-
дачи Майера, действительно, введем новую фазовую перемен-
ную
x
o
= J(x,u),
тогда
(t)x
o
= F( t, x, u ) ,
и расширенный фазовый вектор
(t)x = ( x
o
x
1
,…, x
n
)
т
.

177
Задача Майера для расширенного фазового вектора (t)x и c
функционалом
J(
x , u) = Ф( t
f
, )(tx
f
) = x
o
(t
f
)
→ min
является аналогом задачи Лагранжа (8.29).
З а д а ч а Б о л ь ц а (смешанный функционал), качество
управления определяется функционалом смешанного типа, кото-
рый имеет интегральную и терминальную составляющие
J(x,u) = Ф( t
o
, x(t
o
), t
f
, x(t
f
)) +
∫
f
t
t
0
F(t,x,u) dt → min . (8.31)
Отметим, что данную задачу также можно представить в
форме задачи Майера.
8.3.2. Виды дифференциальных связей.
Вид дифференциальных уравнений, описывающих динами-
ческую систему, представляет собой существенную характери-
стику задачи оптимального управления. В 8.2 были рассмотрены
различные динамические системы и особенности дифференци-
альных уравнений, которыми они описываются. Различают нели-
нейные, линейные, стационарные динамические системы, среди
нелинейных систем дифференциальных уравнений выделяют
системы с разрывными правыми частями. Вид дифференциаль-
ных
уравнений определяет условия применимости теоремы су-
ществования и единственности решения, определяет сходимость
и эффективность алгоритмов поиска решения в различных зада-
чах оптимального управления.
В целом вид динамической системы (модели) определяется
особенностями военно-технической системы, относительно кото-
рой принимается решение. Естественно стремление исследова-
теля (лица, принимающего решение) к разработке наиболее про-
стой
модели - наиболее простым дифференциальным уравнени-
ям, описывающим систему, именно в этом случае создается воз-
можность построения эффективных алгоритмов поиска опти-
мального решения.
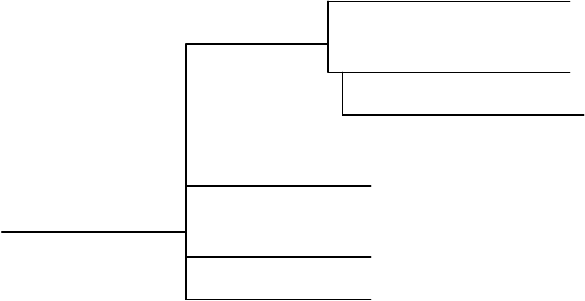
Итак, можно различать следующие основные виды диффе-
ренциальных уравнений, соответственно, динамических систем
(моделей).
178
дифференцируемые
нелинейные
недифференцируемые
с разрывными правыми час-
тями
конечномерные линейные
диффренциальные
динамические
системы автономные
стационарные
8.3.3. Ограничения вдоль траектории.
Дифференциальные уравнения описывают изменение со-
стояния динамической системы при заданном управлении и в за-
висимости от начального и конечного состояния ограничивают
возможные воздействия, прикладываемые к системе на интерва-
ле управления. Вместе с тем на состояния системы могут накла-
дываться дополнительные ограничения, которые, в свою оче-
редь, ограничивают возможные управления, более
того сами
управляющие воздействия должны удовлетворять, как правило,
ряду ограничений.
Как отмечалось ранее, пространство альтернатив Δ пред-
ставляет собой декартово произведение Δ = T×X×U, где T - мно-
жество моментов времени; X - множество состояний системы; U -
множество управлений. Поэтому ограничения, заданные на Δ,
представляют собой конструкцию вида G
t
×G
x
×G
u
⊆ Δ, причем, как
правило, рассматриваются ситуации, когда G
t
= (t
o
,t
f
], в этом слу-
чае ограничения можно представить в виде G
x
(t)×G
u
(t)⊆Δ, t∈(t
o
,t
f
].
Следует отметить, что не зависимо от того, какие элементы про-
странства альтернатив подвергаются ограничениям (время, со-
стояние или управление), обеспечить выполнение этих условий
представляется возможным только на основе выбора соответст-
вующих управлений.
Принято различать следующие способы задания ограниче-
ний вдоль траектории.
179
а). Ограничения на управление. Такого типа ограничения в
общем виде можно представить как
u(t) ∈ G
u
= { u(t) ∈ R
m
⎮ g
i
(t,u) ≤ 0, i∈I
u
} .
Простейший вид таких ограничений, часто используемых в
различных задачах оптимального управления, имеет вид
⎮u (t)⎮ ≤ U
o
.
б). Ограничения на фазовые переменные. Такие ограниче-
ния можно представить в виде
x(t) ∈ G
x
= { x(t) ∈ R
n
⎮ g
i
(t,x) ≤ 0, i∈I
x
} .
Например, движение динамической системы должно проис-
ходить в некоторой "трубке"
⎮x (t)⎮ ≤ a(t) .
в). Совместные ограничения на управление и фазовые пе-
ременные. В ряде случаев ограничения на управление и ограни-
чения на фазовые переменные не могут быть разделены. Тогда
ограничения имеют вид
G
xu
= { x(t) ∈ R
n
, u(t) ∈ R
m
⎮ g
i
(t,x,u) ≤ 0, i∈I
xu
} .
г). Интегральные ограничения (изопериметрические). Как
функционал Лагранжа характеризует некоторое интегральное
качество управления, так и изопериметрические ограничения
описывают требования ко всему интервалу управления (ограни-
чения количества используемого на управление ресурса, напри-
мер)
∫
f
t
t
0
G
i
( t, x, u) dt = A
i
, i = 1,…, z . (8.32)
8.3.4. Краевые условия.
Содержание задач оптимального управления, как правило,
состоит в переводе динамической системы из некоторого началь-
ного состояния в конечное при достижении определенных качест-
венных характеристик управления. В этой связи для постановки
задачи весьма важны начальное и конечное состояния системы,
которые задаются краевыми условиями.
Здесь, прежде всего, принято различать задачи с ф
и к с и-
р о в а н н ы м временем (начальным t
o
= a, или конечным t
f
= b);
и задачи со с в о б о д н ы м временем (начальным t
o
∈R
+
, или
конечным t
f
∈R
+
).
180
Аналогично, с точки зрения задания ограничений на со-
стояние в начальный и конечный момент времени различают за-
дачи:
а). Задача с ф и к с и р о в а н н ы м и концами
- фиксированный левый конец x(t
o
) = A ∈ R
n
,
- фиксированный правый конец x(t
f
) = B ∈ R
n
.
б). Задача со с в о б о д н ы м и концами
- свободный левый конец x(t
o
) ∈ R
n
,
- свободный правый конец x(t
f
) ∈ R
n
.
в). Задача с п о д в и ж н ы м и концами
- подвижный левый конец E
oi
(t
o
,x(t
o
)) = 0, i=1,..,l ≤ n,
- подвижный правый конец E
fj
(t
f
,x(t
f
)) = 0, j=1,..,p ≤ n.
В общем случае совокупность данных равенств определяет
некоторую гиперповерхность на левом (правом) конце фазовой
траектории. Если при задании такой гиперповерхности время не
фиксировано, то говорят о задачах с "перемещающимся много-
образием" на левом (правом) конце.
Анализ особенностей задания рассмотренных четырех
элементов, участвующих в постановке задачи оптимального
управления, позволяет провести
классификацию различных за-
дач и выбрать соответствующий метод решения.
8.4. Примеры задач оптимального управления
Рассмотрим несколько примеров простых задач оптималь-
ного управления, имеющих важные приложения.
8.4.1. Оптимальное управление сближением
космических аппаратов
Два космических аппарата (КА) осуществляют совместное
выполнение целевой задачи в процессе орбитального полета.
Для инспекции технического состояния одного из космических
аппаратов (второго), проводимой путем наружного осмотра, не-
обходимо произвести их сближение. Для проведения сближения
на борту первого КА имеется двигательная установка. Необходи-
мо найти управление двигательной установкой КА, позволяющее
произвести
сближение за минимальное время.
