Мищенко А.М. Сборник задач по линейным электрическим цепям с кратким изложением теории
Подождите немного. Документ загружается.


81
являются корнями его характеристического уравнения
0
1
2
=++
CL
p
L
R
p . Константы
1
I ,
2
I определяются из начальных
условий, например,
0)0(
=
C
u , 0)0(
=
i . В формуле (4.12) введен
параметр
L
R
2
=
δ
определяющий степень диссипации энергии. При
отсутствии диссипации энергии (
0
=
R ) колебания не затухают и имеют
частоту равную собственной (
LC1
0
==
ωω
). Наоборот, при
значительной диссипации энергии (
0
ω
δ
> или
ρ
2>R ) ток в контуре не
совершает никаких колебаний, и при больших временах экспоненциально
затухает. Такой процесс называется апериодическим. В промежуточном
случае слабого затухания (
0
ω
δ
<
или
ρ
2
<
R ) величина тока также
экспоненциально падает. Однако при этом совершается ряд
периодических колебаний
)cos()exp()(
1
ϕ
ω
δ
+
−
=
ttIti
m
. (4.13)
Здесь
22
01
δωω
−=
, а
m
I
и
ϕ
– постоянные интегрирования,
определяемые из начальных условий. Например, при
0)0(
=
C
u , 0)0( =i
постоянные интегрирования:
L
u
I
c
m
1
)0(
ω
=
, а
2
π
ϕ
= .
В электронике особую важность представляют колебательные контуры
со слабым затуханием (
0
ω
δ
<
<
или
ρ
<
<R ). Для их описания
используют ряд параметров, которые широко используются при
рассмотрении процессов колебания любой физической природы.
1. Декремент затухания
L
R
2
=
δ
. Обратная величина от декремента
соответствует времени
δ
τ
1
=
, за которое амплитуда колебаний
уменьшается в
e раз.
2. Логарифмический декремент затухания
T
Tti
ti
l
⋅=
+
=
δδ
)(
)(
ln
, (4.14а)
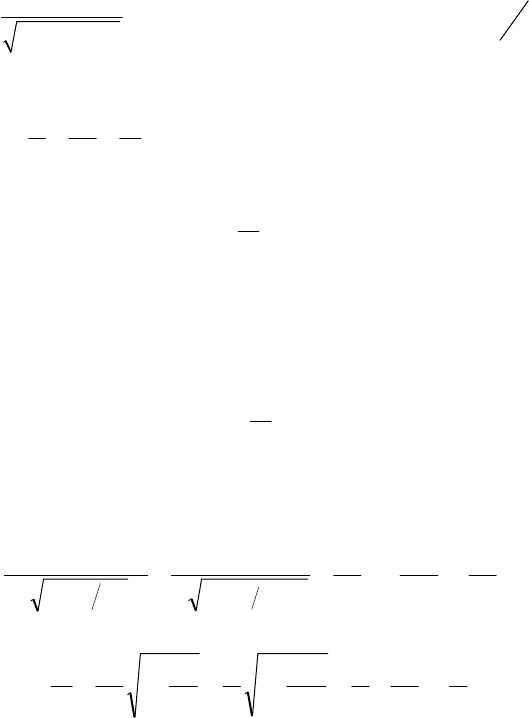
82
где
0
2
0
1(/ )
T
T
δω
=
−
– период затухающих колебаний,
0
0
2
ω
π
=T –
период собственных колебаний. Логарифмический декремент определяет
количество колебаний
N, происходящих за время падения их амплитуды в
e раз:
l
TT
N
δδ
τ
11
===
. Поэтому, логарифмический декремент можно
определить, как обратную величину от
N т. е.
N
l
1
=
δ
, (4.14б)
3. Добротность колебательного процесса обычно определяют
количеством колебаний за время падения их амплитуды в
e раз. Для
количественного совпадения вводимой таким образом добротности с
добротностью, определяемой в радиоэлектронике по ширине резонансных
максимумов, используется корректирующий множитель равный
π:
l
NQ
δ
π
π
== . (4.15)
Логарифмический декремент затухания последовательного контура
при слабом затухании
0
ω
δ
<
<
(
ρ
<
<R ), согласно полученному
выражению (4.12), рассчитывается по формуле:
ρ
π
ρ
ρ
π
ρρ
π
ωδω
πδ
δ
RRR
R
R
l
≈+≅
−
=
−
= )
8
1(
)2(1)(1
2
2
2
22
00
,
а добротность контура – по формуле:
R
R
R
R
R
Q
l
ρ
ρ
ρ
ρ
ρ
ω
δ
δ
ω
δ
π
≈−≅−=−== )
8
4
11
2
2
2
2
0
2
0
.
Видно, что расчеты добротности по формулам (4.14), (4.15) с хорошей
точностью приводят к тому же самому результату, что и при расчете по
формуле (4.3), которая была получена из анализа вынужденных
колебаний, а точнее говоря из частотной зависимости модуля
комплексного сопротивления контура. Точность совпадения та же самая,
что и при расчете
Q по формуле (4.8).
Резонансные явления в стационарном режиме в цепи с подключенным
источником энергии и собственные колебания определяются только
свойствами самой цепи (с учетом схемы источника), поэтому
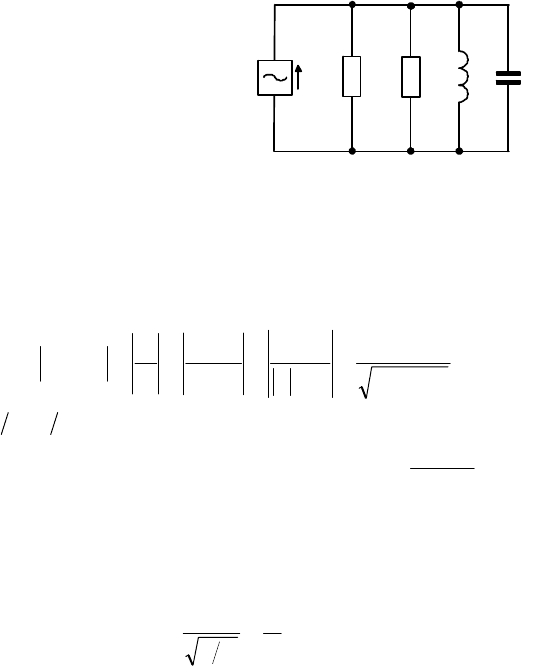
83
добротность, собственная и резонансная частота совпадают для цепей с
малой величиной диссипации энергии.
Параллельный колебательный контур
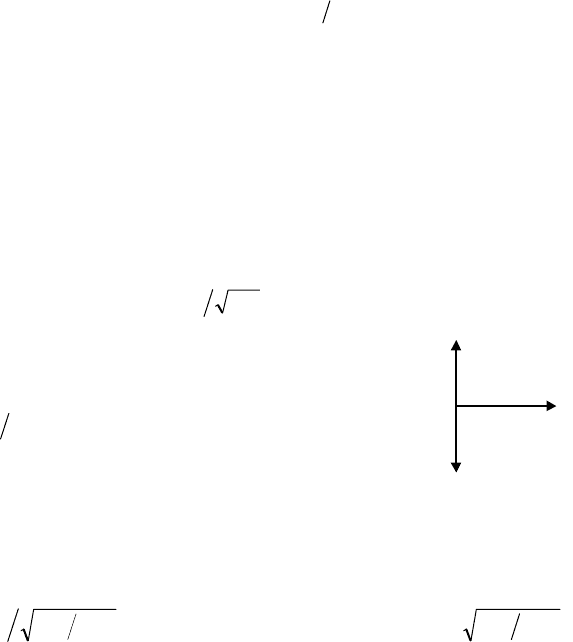
Вынужденные колебания. Резонанс токов. В стационарном
состоянии в параллельном колеба-
тельном контуре под действием
источника тока происходят выну-
жденные колебания напряжения.
Это напряжение наиболее просто
находятся методом комплексных
амплитуд. Мгновенное значение
напряжения на
простом колеба-
тельном контуре (рис. 4.5), пи-
таемого источником тока
)sin()(
ψ
ω
+
=
tIti
m
с внутренним
сопротивлением
0
R , равно
)sin()(
1
ψ
ω
+
=
tUtu
m
. (4.16)
Амплитуда напряжения
22
0
1
U
0
1
xQ
RI
eY
eI
Y
eI
Y
I
eU
m
j
j
m
j
m
j
mm
+
=====
ψ
ψψ
ψ
&
, (4.17)
где
CjLjRY
ω
ω
++= 11 – комплексная проводимость контура с
учетом внутреннего сопротивления источника тока,
10
10
RR
RR
R
+
=
– общее
сопротивление контура, Ψ
1
и Ψ – фазы напряжения на контуре и тока
источника, а Ψ
0
– аргумент комплексной проводимости контура. При
преобразовании модуля комплексной проводимости контура введен
параметр
Q , который называется добротностью параллельного контура
ρ
R
CL
R
Q ==
. (4.18)
Относительная расстройка (х) и входящая в нее собственная частота
контура (ω
0
), определяются по формулам (4.5) и (4.6). Амплитудно-
частотная характеристика напряжения на параллельном контуре
полностью определяется модулем комплексной проводимости контура.
Характер формул (4.17) и (4.2) одинаков, поэтому она точно такая же, как
и у тока в последовательном контуре. Максимальное значение амплитуды
R
0
L
i(t)
C
R
1
Рис. 4.5
84
напряжения на контуре
RIU
mm
=
0
достигается при
ω
=
ω
0
, когда
проводимость контура становиться минимальной; максимум
0m
U тем
выше и острее, чем больше добротность контура. Полуширина спектра
связана с добротностью контура тем же выражением (4.8). Однако, в
данном контуре с ростом сопротивления резистора полоса пропускания
уменьшается из-за того, что при этом растет его добротность. Поэтому
параллельные резонансные контуры обычно используют с источниками, у
которых активное внутреннее сопротивление
много больше активного
сопротивления контура.
Сдвиг фазы между током и напряжением равен аргументу
комплексной проводимости:
QxLCRtgtg
=
−
=
=
− )1()(
01
ω
ω
ψ
ψ
ψ
. (4.19)
Разность фаз
1
ψ
ψ
−
между втекающим в контур током и поданным
напряжением равна нулю при резонансной частоте ω = ω
0
. Поэтому
частота
ω
0
является ещё и резонансной, т. е
р
ω
ω
=
0
. Условие равенства
фаз напряжений и токов в электронике является основным для
определения резонансных частот. Математически для параллельного
контура оно соответствует требованию равенства нулю реактивной
(мнимой) части полной комплексной проводимости контура:
0)(Im
=
р
Y
ω
. (4.20)
Для простого параллельного колебательного контура (рис. 4.5)
условие (4.20) дает
LC
р
1=
ω
и обеспечивает
минимальный модуль его комплексной проводимости.
На резонансной амплитуде токи в емкости
(
00
IjQejQICjUI
j
mC
&&&
===
ψ
ω
) и в индуктивности
(
00
IjQejQILjUI
j
mL
&&&
−=−==
ψ
ω
) равны и
противоположны по направлению. Поэтому о
резонансе в параллельных контурах, принято говорить
как о резонансе токов. Диаграмма токов при резонансе
показана на рис. 4.6.
При резонансе токов величины токов в емкости и индуктивности в Q
раз больше втекающего тока. Однако, они не максимальны.
Максимальная амплитуда тока в емкости достигается
при
2
0
211 Q
C
−=
ωω
, а в индуктивности – при
2
0
211 Q
L
−=
ωω
.
Убедиться в этом можно приравниванием нулю производных от модуля
I
R
=I
0
I
C
I
L
+j
+
Рис.4.6

85
токов
Y
CE
d
d
I
d
d
m
C
ω
ωω
=
&
и
YL
E
d
d
I
d
d
m
L
ωωω
=
&
. Амплитудно-
частотные характеристики тока конденсатора и индуктивности в
параллельном контуре подобны аналогичным характеристикам
напряжений, соответственно, на индуктивности и на конденсаторе в
последовательном контуре.
Для контуров с большой добротностью, обычно используемых на
практике, различия между
ω
C
, ω
L
и
ω
0
или
ω
р
практически нет. Поэтому,
как и в случае последовательного колебательного контура, резонанс в
параллельном контуре понимается только в смысле отсутствия сдвига
фаз между напряжением и током контура, т.е. когда комплексная
проводимость цепи становиться чисто вещественной.
Свободные (собственные) колебания. Физический метод
определения параметров колебательного контура. Собственные
колебания, как и
в последовательном контуре, возникают в отсутствии
принуждающего переменного воздействия. Например, в случае, когда
заряженная емкость разряжается через параллельное соединение
индуктивности с резистором. Напряжение на контуре определяется
интегро-дифференциальным уравнением, вытекающим их первого закона
Кирхгофа
0)0(
1
0
=+++
∫
L
t
iudt
LR
u
dt
du
C , (4.21)
где i
L
(0) – ток в индуктивности в начальный момент времени (t = 0).
Уравнение (4.21) аналогично уравнению (4.10). При отсутствии потерь
энергии в контуре (
∞
=
R
) напряжение будет соответствовать
периодическим незатухающим колебаниям с собственной частотой
контура
LC1
0
=
ω
. Если потери энергии за период собственных
колебаний значительны, то второе слагаемое в уравнении (4.21)
доминирует над третьим, и напряжение экспоненциально падает, не
совершая колебаний. Это наглядно видно из приведенного ниже
выражения для корней характеристического уравнения. В промежуточном
случае слабых затуханий (1/2RC < ω
0
) возникают периодические
колебания напряжения с экспоненциальным падением амплитуды.
)cos()exp()(
1
ψ
ω
δ
+
−
= ttUtu
m
. (4.22)
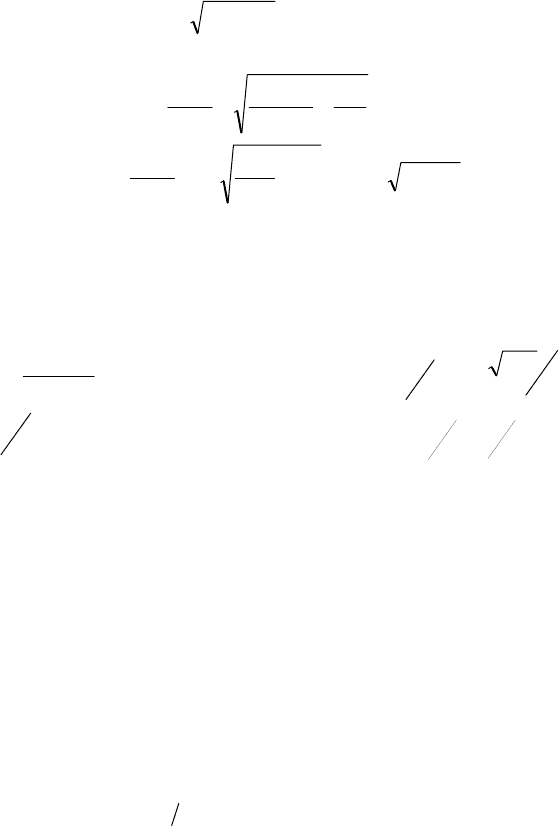
86
Алгебраические выражения для декремента затухания
)2/(1 RC
=
δ
и
частоты колебаний
22
01
δωω
−= следуют из формул для корней
характеристического уравнения
.1
4
2
1
1
4
1
2
1
0
2
2
0
22
2,1
δωδ
ρ
ω
−±−=−±−=
=−±−=
j
R
RC
LC
CR
RC
p
(4.23)
Откуда следуют условия на разделение колебаний по уровню диссипации
энергии: при
0
ω
δ
> или R2>
ρ
колебания апериодические; при
0
ω
δ
<
или
R2<
ρ
– затухающие. Постоянные интегрирования
m
U
&
и Ψ
определяются из начальных условий.
Логарифмический декремент затухания напряжения на контуре
(
T
Ttu
tu
l
δδ
=
+
=
)(
)(
ln
) при
0
ω
δ
<
< равен
=≈
0
2
ω
πδ
δ
l
=
RC
LC
π
R
ρ
π
= , а добротность параллельного контура
ρδ
π
R
Q
l
=≈
. Видно,
что проведенный расчет добротности по формулам (4.14), (4.15) приводит
к такому же результату, что и при расчете по формуле (4.18). Точность
совпадения та же самая, что и при расчете Q по формуле (4.18).
Резонансные явления в стационарном режиме в цепи с подключенным
источником энергии и собственные колебания определяются только
свойствами самой цепи (с
учетом схемы источника), поэтому
добротность, собственная и резонансная частота совпадают для цепей с
малой величиной диссипации энергии.
Резонансы в сложных контурах
Сложные контуры, состоящие из многих ветвей с емкостями и
катушками индуктивности, имеют несколько резонансных частот. Для
определения какая частота относиться к последовательному, а какая к
параллельному резонансу удобно все активные
сопротивления в цепи
положить равными нулю. Тогда, полное сопротивление контура или его
проводимость (
)(1)(
ω
ω
ZY = ) является чисто мнимой величиной, а
следовательно, частоты, при которых выполняется условие
0))(Im(
=
ω
Z или
∞
=
))(Im(
ω
Y , соответствуют последовательному
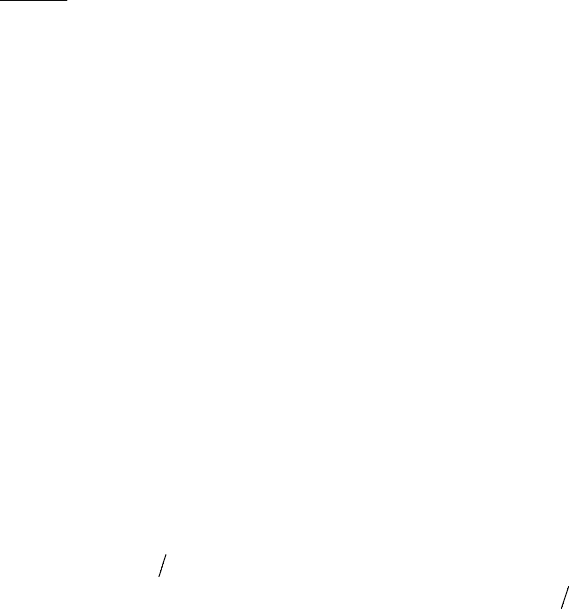
87
резонансу, а частоты при выполнении условия
0))(Im(
=
ω
Y или
∞
=
))(Im(
ω
Z – параллельному резонансу.
Качественный анализ цепи на наличие резонансов и получения
приблизительных значений резонансных частот полезно проводить,
используя теорему Фостера.
Теорема Фостера. Если сопротивление цепи
)()(
ω
ω
jXZ
=
является
чисто мнимым, то оно описывается неубывающей функцией, а именно:
0
)(
>
ω
ω
d
dX
. Следствия из этой теоремы:
1) точки
0=
ω
и
∞
=
ω
есть особые точки (нули или полюсы
входного сопротивления);
2) на оси
ω
нули и полюсы расположены в чередующемся порядке;
3) в электрической цепи, составленной из n реактивных элементов,
возникает не более n-1 резонанса.
Иными словами:
• все частотные характеристики входных сопротивлений и
проводимостей цепей являются возрастающими функциями от частоты;
• резонансы тока и напряжения чередуются между собой;
• если в цепи есть
путь для прохождения постоянного тока, т. е. при
0=
ω
0
вх
=Z (частотная характеристика начинается с нуля), то первым
наступает резонанс токов, если нет (т. е. при
0
=
ω
∞
=
вх
Z ), то первым
наступает резонанс напряжений.
Применение теоремы Фостера особенно эффективно в сочетании с
графическим методом. Этот метод основан на построении графиков
частотной зависимости реактивного сопротивления (или проводимости)
контура. Сопротивления всех резисторов приравнивают нулю.
Основными элементами построения графиков являются частотные
характеристики реактивных элементов. Частотная характеристика
сопротивления индуктивности (
LjZ
L
ω
ω
=
)( ) имеет линейную
зависимость (рис. 4.7, а), а частотная характеристика сопротивления
емкости (
CjZ
C
ω
ω
−=)( ) является гиперболой (рис. 4.7, б). Наоборот –
частотная зависимость проводимости индуктивности (
LjY
L
ω
ω
−
=
)( )
является гиперболой (см. рис. 4.7, б), а частотная характеристика
проводимости емкости (
CjY
C
ω
ω
=
)( ) есть прямая (см. рис. 4.7, а).
Графические построения обоснованны возможностью использования
процедур сложения графиков и обратных преобразований
)(
ω
Z в )(
ω
Y
88
и наоборот
)(
ω
Y в )(
ω
Z . Поэтому построение графика сопротивления
контура (или его проводимости) начинают с выделения элементов в
контуре, имеющих последовательное (или параллельное) соединение
емкости и индуктивности, т. е. с выделения простых последовательных и
параллельных контуров.
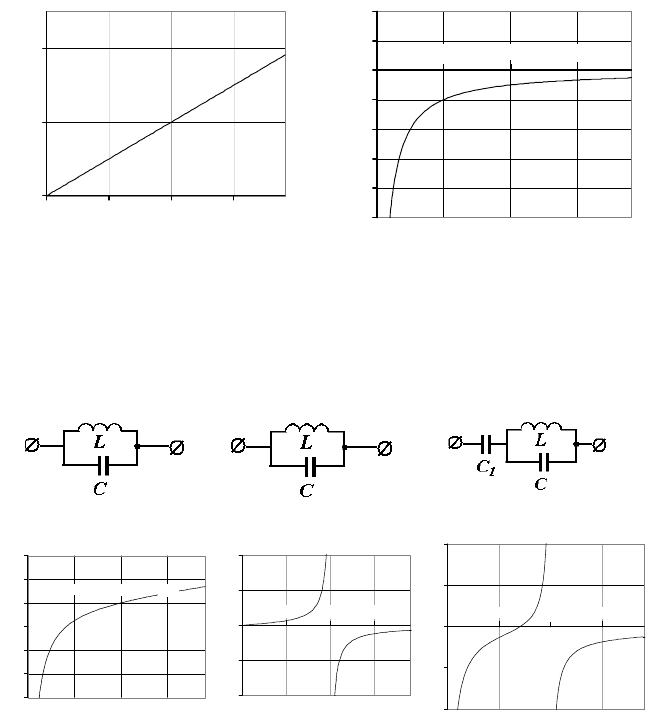
На рис. 4.8 приведены последовательные построения графика
сопротивления сложного контура (рис. 4.8, в). Построения начинают с
прорисовки графика проводимости параллельного контура (
рис 4.8, а), так
как он получается простым сложением графиков проводимости емкости и
индуктивности. Затем этот график преобразуют в график сопротивления
контура (рис 4.8, б) и наконец, в график суммы графиков сопротивлений
параллельного контура и емкости (рис. 4.8, в).
0
1
2
00.511.5
ω
Z
L
,
Y
C
а
-10
-8
-6
-4
-2
0
2
4
0 0. 5 1 1.5
ω
Y
L
,
Z
C
0.5 1 1.5
б
Рис. 4.7
а
б
в
-8
-6
-4
-2
0
2
4
0 0. 5 1 1. 5
ω
Y
0.5
1 1.5
а
-10
-5
0
5
10
0 0.5 1 1.5
ω
Z
0.5 1 1.5
б
-10
-5
0
5
10
0 0.5 1 1.5
ω
Z
0.5 1 1.5
в
Рис 4.8
89
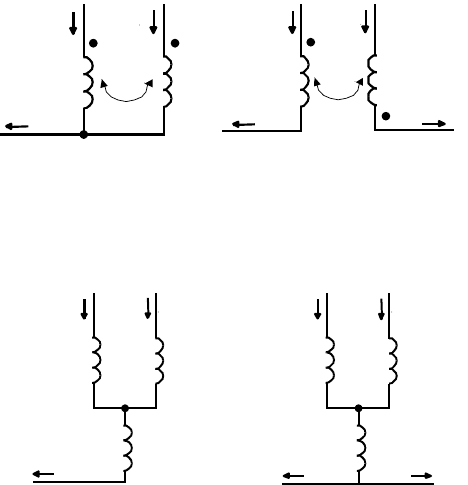
Резонансы в контурах cо взаимной индукцией
Сложные цепи с взаимной индукцией имеют катушки индуктивности
(L
1
и L
2
), которые входят в разные замкнутые контуры и связаны между
собой магнитным полем, через взаимную индуктивность M. Благодаря
этой индуктивности, изменение тока в первом контуре вызывает
изменение тока во втором контуре. Различают согласное (прямое) и
встречное (обратное) включение катушек. При согласном включении
токи, протекающие в катушках в одном направлении, создают потоки
самоиндукции и взаимноиндукции так же в одном направлении. На схеме
это включение отображается жирными точками, лежащими друг против
друга (рис. 4.9, а), а в расчетах знак M берется положительным. При
встречном включении потоки самоиндукции и взаимоиндукции
противоположны. На схеме это включение отображается жирными
точками, ле-
жащими по диа-
гонали
(рис 4.9, б), а
в
расчетах знак M
берется отрица-
тельным. Для
изменения
характера вклю-
чения катушек
достаточно
переключить зажимы одной из двух. Рассматриваемые катушки могут,
как иметь общий узел (рис 4.9, а), так и не иметь (рис 4.9, б).
Определение
количества резо-
нансов в токах и
их типы эффектив-
но проводить,
используя эквива-
лентные схемы,
в
которых индук-
тивно связанные
катушки заменя-
ются катушками
соединенные
звездой. Рис. 4.10 иллюстрирует такую эквивалентную замену реальных
схем приведенных на рис. 4.9. Замена катушек индуктивности
1
L и
2
L
M
L
1
L
2
I
1
I
2
I
3
М
а
M
L
1
L
2
I
1
I
2
I
1
I
2
М
б
Рис. 4.9
M
L
1
- M
L
2
-
M
I
1
I
2
I
3
М
а
L
1
+M
L
2
+M
I
1
I
2
I
1
I
2
-M
М
б
Рис. 4.10
90
E
R L
R
1
C
соответственно на катушки ML
−
1
и ML
−
2
, для случая согласного
включения, и на катушки
ML
+
1
и ML
+
2
, для случая встречного
включения, обеспечивает неизменность втекающих и вытекающих токов,
а так же потенциалов в местах замены одной схемы на другую. Для
контуров, не имеющих общих узлов, а связанных только взаимной
индукцией (рис 4.9, б), введение взаимной индукции в эквивалентную
схему можно проводить с любой стороны катушек. Например, на
рис. 4.10. б приведено преобразование относительно нижних концов
катушек. В этом случае за точку отсчета потенциалов в связанных
контурах удобно брать от возникшего внизу общего узла.
Эквивалентные схемы связанных контуров эффективно используются
для проведения расчетов, так как они позволяют непосредственно
применять к ним все ранее рассмотренные способы расчета
электрических цепей. Особенно эффективно применение метода
эквивалентного генератора, например, для нахождения резонансов виз
выделенных контуров. С этой целью, получают выражение для тока k-ой
ветви данного контура в виде
EYI
kk
&&
=
, где )(1
внkk
ZZY
+
=
–
эффективная проводимость, выраженная через внутреннее сопротивление
эквивалентного генератора (
вн
Z ) и сопротивление k-ой ветви (
k
Z ), а
Е
&
–
приложенное к цепи напряжение (напряжение холостого хода). Далее
находят резонансные частоты при которых амплитуда тока имеет
экстремумы.
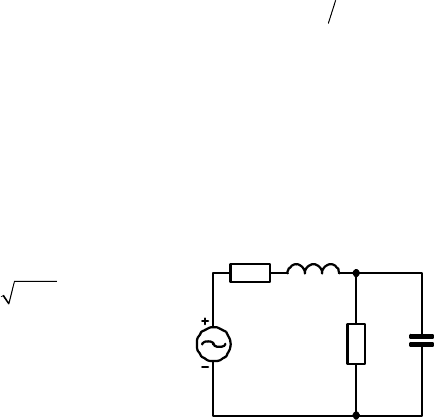
Пример 1. Расчет параметров последовательного колебательного
контура по его комплексному сопротивлению. Для схемы, приведенной на
рис. 4.11, найдем резонансную
частоту, добротность контура и
полосу пропускания. При условии
1
/1R
ρ
<< , где /LC
ρ
= – вол-
новое сопротивление. В этой схеме
идеальный источник напряжения
Е
питает колебательный контур,
состоящий из резистора R, индук-
тивности и емкости имеющей
диэлектрик с конечной прово-
димостью. Она изображена в виде
резистора R
1
, включенного параллельно конденсатору. Источник
напряжения, емкость и индуктивность образуют замкнутый контур.
Рис. 4.11
