Мищенко А.М. Сборник задач по линейным электрическим цепям с кратким изложением теории
Подождите немного. Документ загружается.

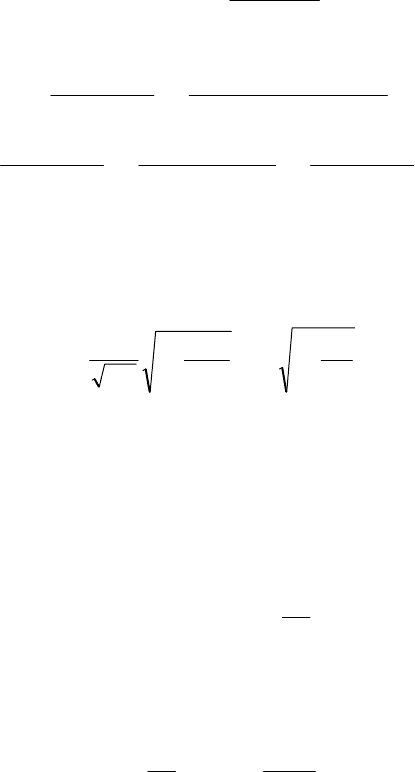
91
Поэтому, несмотря на наличие резистора R
1
, данная цепь является после-
довательным колебательным контуром.
Проанализируем резонансные явления в контуре методом
комплексных амплитуд. Комплексное сопротивление контура
1
1
1
)(
CRj
R
LjRZ
ω
ωω
+
++=
. (4.24, а)
Преобразуем его к виду
.
)(1)(1)(1
)(1
)1(
)(1
)(
2
1
2
1
2
1
2
1
23
2
1
1
2
1
2
2
1
2
1
1
CR
CR
j
CR
LRCL
j
CR
R
R
CR
CLCRL
j
CR
R
RZ
ω
ω
ω
ωω
ω
ω
ωωω
ω
ω
+
−
+
+
+
+
+=
=
+
−+
+
+
+=
(4.24, б)
Первые два слагаемых в равенстве (4.24, б) можно рассматривать как
некоторый резистор с эффективным сопротивлением, а два последних –
как соответственно сопротивления эффективных индуктивности и
емкости.
Возникновение резонанса будет происходить при частоте
2
1
2
0
2
1
11
1
RCR
L
LC
р
ρ
ωω
−=−=
, (4.25)
обеспечивающей выполнение условия
0)(Im
=
ω
Z . При этой частоте ток
и ЭДС источника находятся в фазе и величина тока максимальна.
Отметим, что свободные колебания в контуре возникают лишь при
условии
1
/
R
ρ
< 1, когда резонансная частота вещественна. Нарушение
этого условия исключает возникновение колебаний (см. пример 2).
Подставляя полученную частоту в уравнение (4.24) получаем
сопротивления контура
1
2
))(Re()(
R
RZZ
рр
ρ
ωω
+==
. (4.26)
Оно отвечает за рассеивание мощности контуром на резонансной частоте.
В первом приближении по
1
/
R
ρ
резонансная частота ω
р
≈ ω
0
, а
комплексное сопротивление в окрестности ω
0
:
Cj
Lj
R
RZ
0
0
1
2
1
)(
ω
ω
ρ
ω
+++≈ , (4.27)

92
т. е. оно соответствует простому последовательному контуру (рис. 4.1) с
эффективным резистором
1
2
R
RR
эф
ρ
+≈
и с емкостью и индуктивностью,
как в исходном контуре. Поэтому добротность контура находится как
1
2
R
R
R
Q
эф
ρ
ρρ
+
=≈
. (4.28)
Влияние на добротность сопротивления R
1
тем меньше, чем лучше
выполняется неравенство
1
/
R
ρ
<< 1. Приведенное решение корректно
при наличии большой добротности не менее ≈ 10, когда сопротивление
R
эф
практически постоянно в полосе пропускания контура.
Пример 2. Расчет параметров последовательного колебательного
контура физическим методом. В качестве примера проанализируем
работу схемы на рис. 4.11 в режиме собственных колебаний при
короткозамкнутом источнике. Будем для определенности полагать, что в
конуре в начальный момент емкость заряжена, а тока в контуре нет.
Запишем систему уравнений
Кирхгофа в интегро-дифференциальном виде
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=−−
=−−
=++
∫
,0
,0)0(
1
,0
321
0
321
21
1
1
iii
udti
C
iR
iR
dt
di
LRi
C
t
(4.29)
где i
1
, i
2
и i
3
– соответственно, токи в резисторах R, R
1
и емкости, u
C
(0) –
начальное напряжение на емкости. Дифференцируя второе уравнение и
осуществляя замену i
3
, получаем систему
⎪
⎩
⎪
⎨
⎧
=−−
=++
.0
11
,0
2
121
21
1
1
dt
di
Ri
C
i
C
iR
dt
di
LRi
(4.30)
Заменяя
dtd / на p, находим характеристическое уравнение
0)(
11
2
1
=++++ RRpLRCRCLpR . (4.31)
Корни этого уравнения
93
22
1
2
0
1
2
0
2,1
)(1)(
2
ρ
ρ
ω
ρ
ρ
ω
R
Rj
R
Rp −−±+−=
. (4.32)
Откуда следует, что собственные колебания с частотой
22
1
2
0
)(1
ρ
ρ
ωω
R
R −−=
возникают в контуре лишь при
положительном подкоренном выражении, т. е. при малом
логарифмическом декременте затухания (
1
1
<+
R
R
ρ
ρ
). При выполнении
этого условия добротность контура
1
2
01
2
0
1
2
0
2
)(
2
1
)(
2
1
R
R
R
RT
R
R
Q
ρ
ρ
ω
πρ
ρ
ω
π
ρ
ρ
ω
π
+
=
+
≈
+
=
. (4.33)
Подчеркнем, что найденная добротности с хорошей точностью
совпадает с добротностью, рассчитанной по импедансу контура в
предыдущем примере.
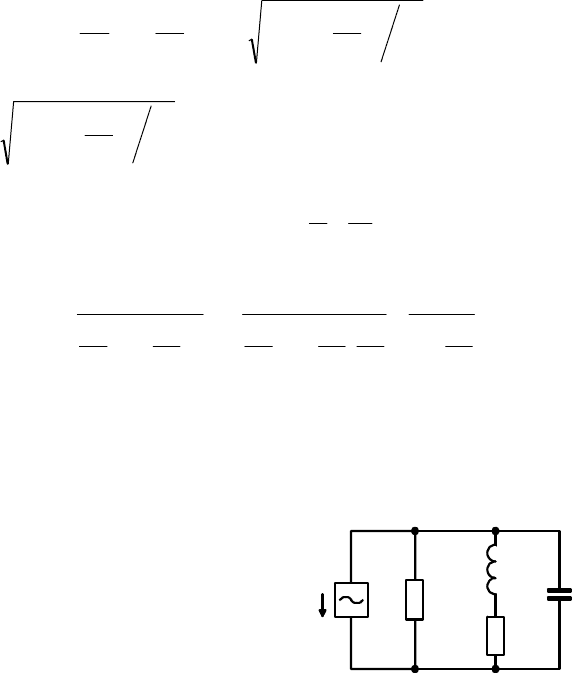
Пример 3. Расчет параметров параллельного колебательного
контура по его комплексной проводимости. Рассмотрим параллельный
контур, изображенный на рис. 4.12.
Источник тока
0
I
с внутренним
сопротивлением R
0
питает колеба-
тельный контур, состоящий из
идеального конденсатора C и ка-
тушки индуктивности L с потерями,
которые учитываются последо-
вательно включенным резистором R.
Найдем резонансную частоту и
добротность контура.
В этом контуре ветви, содержащие емкость и индуктивность,
параллельны и параллельно присоединены к источнику. Поэтому контур
является параллельным колебательным контуром. Решение
проведем
методом комплексных амплитуд.
Комплексная проводимость контура
R
L
C
R
0
I
0
Рис. 4.12
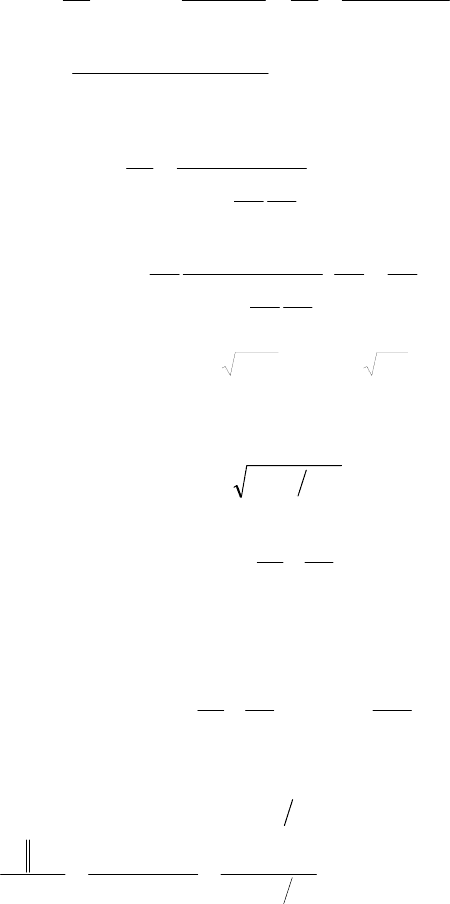
94
.
)(
)(
111
)(
22
223
22
00
LR
LCRCL
j
LR
R
RLjR
Cj
R
Y
ω
ωωω
ωω
ωω
+
−+
+
+
+
+=
+
++=
(4.34, а)
Преобразуем её к виду:
.)1(
)1(
)1(
11
)(
2
2
2
0
2
2
2
2
0
2
2
2
0
2
2
2
2
0
2
0
−+
+
+
+
+
+=
ρω
ω
ρ
ω
ω
ρ
ω
ω
ρ
ω
ω
ω
R
R
R
j
R
R
R
Y
(4.34, б)
В выражениях (4.34, а, б)
CL /=
ρ
, LC/1
0
=
ω
. Резонансная частота
находится из равенства нулю мнимой части проводимости. Исключая
случай постоянного тока (ω = 0), резонанс в контуре может возникнуть
при
/R
ρ
< 1 c частотой
2
0
)(1
ρωω
R
p
−=
. (4.35)
Проводимость контура на резонансной частоте вещественна
2
0
1
)(
ρ
ω
R
R
Y
р
+=
. (4.36)
Она определяет рассеивание энергии контуром.
В первом приближении по
/R
ρ
выражение для проводимости контура в
окрестности резонансной частоты упрощается:
)
1
(
1
)(
0
0
2
0
L
Cj
R
R
Y
ω
ω
ρ
ω
−++≈
, (4.37)
приобретая вид, простого параллельного колебательного контура
(рис. 4.5) с емкостью и индуктивностью как в исходном контуре, но с
эффективным резистором
RR
эф
2
ρ
≈ Поэтому добротность контура
0
2
0
0
0
)(
RR
RR
RR
RR
Q
эф
эф
эф
ρ
ρ
ρρ
+
≈
+
=≅
и она тем точнее соответствует
95
истинной, чем меньше отношение
/R
ρ
. Откуда следует, что при
эф
RR >
0
источник тока не влияет на добротность ( RRQ
эф
ρ
ρ
=
≅
) и
на колебательные процессы в контуре. Поэтому добротность становится
равной добротности последовательного контура, состоящего из
индуктивности
L , емкости
С
и сопротивления
R
. Наоборот, при
эф
RR <
0
добротность контура будет определяться величиной
внутреннего сопротивления источника
0
/QR
ρ
≈
.
Полученное решение корректно при наличии большой добротности не
менее ≈ 10, когда сопротивление
эф
R
практически постоянно в полосе
пропускания контура.
Пример 4. Расчет параметров параллельного колебательного
контура физическим методом. Проанализируем работу схемы,
приведенной на рис. 4.12 в режиме собственных колебаний, когда
источник тока отключен, но его внутреннее сопротивление
0
R оставлено.
Начальным состоянием контура выберем состояние, в котором токи
отсутствуют, а конденсатор имеет напряжение u
C
(0). Систему уравнений
Кирхгофа в интегро-дифференциальном виде запишем через напряжения
на элементах цепи
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
=+
=++
∫
∫
.
1
,
,0
1
0
0
0
R
u
dtu
L
uuu
dtu
LR
u
dt
du
C
R
t
L
CRL
t
L
CC
(4.38)
Дифференцируя уравнения и исключая из второго и третьего
напряжение u
R
, получаем систему однородных дифференциальных
уравнений
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=−−
=++
.0
111
,0
11
0
2
2
L
L
C
L
CC
u
Ldt
du
Rdt
du
R
u
Ldt
du
R
td
ud
C
(4.39)
Преобразуем ее в одно дифференциальное уравнение
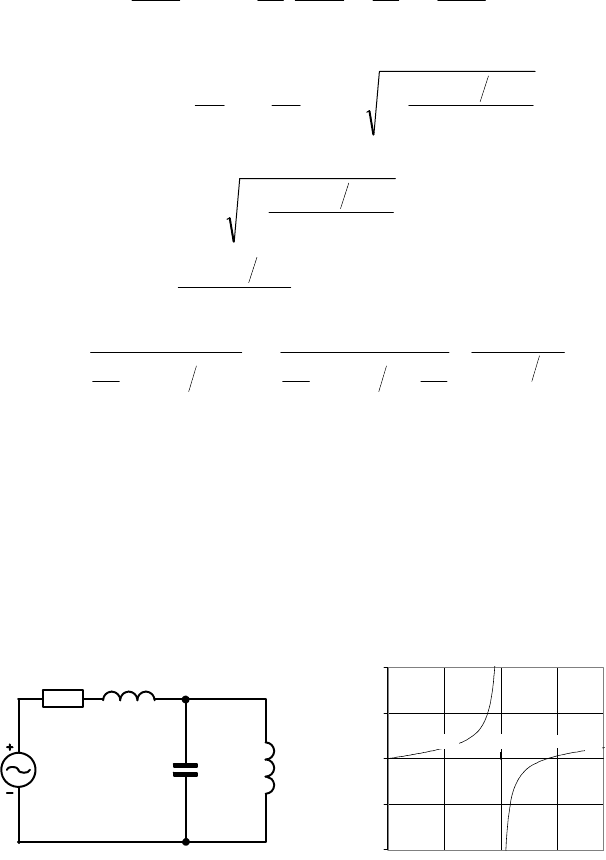
96
0)1()(
0
2
2
0
3
3
=++++
dt
ud
R
R
dt
ud
R
L
CR
dt
ud
LC
CCC
(4.40)
и найдем корни его характеристического уравнения
р
1
= 0 и
2
2
0
2
0
0
2
0
3,2
4
)(
1)(
2
ρ
ρ
ω
ρ
ρ
ω
RR
j
R
Rp
+
−±+−=
. (4.41)
Откуда собственные колебания в цепи с частотой
2
2
0
2
0
4
)(
1
ρ
ρ
ωω
RR +
−=
(4.42)
возникнут лишь при
1
2
)(
0
2
<
+
ρ
ρ
RR
и добротность цепи будет
0
2
0
2
0
0
2
0
2
)(
2
1
)(
2
1
RR
RRTRR
Q
ρ
ρ
ω
π
ρ
ρ
ω
π
ρ
ρ
ω
π
+
≈
+
≈
+
=
. (4.43)
Найденное выражение для добротности в области сделанных
приближений аналогично зависимости полученной на основе анализа
комплексной проводимости.
Пример 5. Резонансы в сложном контуре. В качестве примера
рассмотрим схему, приведенную на рис. 4.13. Она состоит из
двухполюсника (сложного резонансного контура) питаемого источником
ЭДС. В данном контуре согласно теореме Фостера должны возникать
(
21 =−n ) два резонанса: сначала резонанс токов, а затем резонанс
напряжений. Частотная характеристика реактивного сопротивления Z
этого двухполюсника (общее сопротивление всех индуктивностей и
R
L
1
C L
2
E
а
-10
-5
0
5
10
0 0,5 1 1, 5
ω
Z
0.5 1
1.5
б
Рис. 4.13
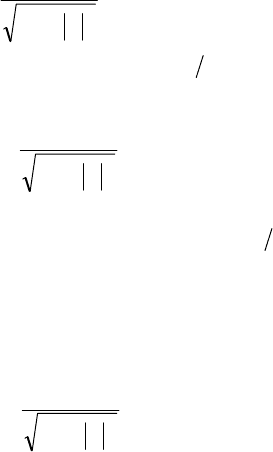
97
емкости), показана на рис. 4.13, б. Она получается сложением графика
сопротивления параллельного контура (рис. 4.8, б) с графиком
сопротивления индуктивности (рис. 4.7, а). Видно, что двухполюсник
имеет два резонанса один параллельный на частоте соответствующей
месту разрыва в спектре и один последовательный на частоте пересечения
спектра с осью частот. Ток, втекающий в двухполюсник (ток
через
резистор), определяется выражением
)sin()(
2
2
ψω
+
+
= t
ZR
E
ti
, (4.44)
где
Е
– амплитуда источника ЭДС, )( RXarctg
=
ψ
– фаза тока (фаза
ЭДС принята за нуль). Отсюда амплитуда напряжения
R
U
&
на резисторе
2
2
ZR
ER
U
R
+
=
, (4.45)
Следовательно, спектр амплитуды тока или напряжения на резисторе
имеет максимальные значения равные соответственно
RE и
E
при
0=Z
, т. е. при нулевой частоте и при частоте последовательного
резонанса. Минимальные, нулевые значения тока и напряжения на
резисторе возникают при
∞
=
Z
, когда частота равна частоте
параллельного резонанса или переходит в высокочастотную область
(
∞⇒
ω
). На реактивном сопротивлении контура амплитуда напряжения
2
2
ZR
EZ
U
X
+
=
. (4.46)
Поэтому, наоборот, на нулевой частоте и на частоте последовательного
резонанса амплитуда напряжения имеет минимальные значения равные
нулю, а на частоте параллельного резонанса и в высокочастотной области
она достигает максимальных значений равных
E
.
Рассмотрение особенностей в спектрах напряжений в понятиях
последовательного и параллельного резонансов позволяет качественно
объяснить изменения в спектрах с изменением величины сопротивления
резистора. Например, увеличение сопротивления будет вызывать
увеличение добротности для параллельного резонанса, а следовательно, к
сужению спектра в этой области частот. Наоборот, в случае
последовательного резонанса рост сопротивления резистора будет
приводить к уменьшению добротности последовательного резонанса, а,
следовательно, к уширению спектра в этой области частот.
98
Пример 6. Резонансы в контурах с взаимной индукцией. Рассмотрим
резонанс в связанных контурах, изображенных на рис. 4.14. Изменение
тока в первом контуре вызывает изменение тока во втором контуре,
благодаря взаимной индукции М. В рассматриваемой цепи взаимная
индуктивность положительна (на схеме трансформатора жирные точки
лежат друг против друга). Контуры не имеют общих
узлов. Поэтому в
эквивалентной схеме дополнительную катушку индуктивности,
отвечающую за взаимную индуктивность М, можно вводить, как сверху,
так и снизу. На рис. 4.14, б она введена снизу и направление токов в
контурах выбрано так, чтобы отсчитывать потенциал от нижнего узла.
Установившиеся процессы в этих контурах описываются уравнениями
Кирхгофа, которые получаются как
непосредственно по исходной схеме, с
прямым учетом взаимной индукции, так и по эквивалентной схеме:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+++=
+++=
1222
2
22
2111
1
11
1
0
1
IMjIRI
Cj
ILj
IMjIRI
Cj
ILjE
&&&&
&&&&&
ω
ω
ω
ω
ω
ω
(4.47)
Решение системы (4.47) дает:
ток в первом контуре
)(
2
21
2
21
1
nXXjnRR
E
I
−++
=
, (4.48)
ток во втором контуре
22
12
jXR
Mj
II
+
−=
ω
, (4.49)
R
1
L
1
C
1
R
2
E
L
2
M
C
2
а)
R
1
L
1
-M
C
1
R
2
E
L
2
-M
M
C
2
б)
Рис. 4.14

99
где введены обозначения
111
/1 CLX
ω
ω
−
=
,
222
/1 CLX
ω
ω
−
=
и
коэффициент трансформации
2
2
2
2
22
XR
M
n
+
=
ω
.
Входное сопротивление системы двух связанных контуров:
)()(
11
2
21
2
21
1
внвнвх
XXjRRnXXjnRR
I
E
Z −++=−++== , (4.50)
Вид входного сопротивления позволяет представить систему рас-
сматриваемых контуров, как один контур с эффективными элементами,
зависящими от частоты. Дополнительное активное (
2
2
nRR
вн
= ) и
реактивное (
2
2
nXX
вн
= ) сопротивления (их называют внесенными)
возникают за счет индуктивной связи и при разрыве её (
0
=
M ) исчезают.
Определение количества резонансов в первом контуре, их тип и
качественное представление спектра тока наиболее просто провести
графическим методом, используя эквивалентную схему (рис. 4.14, б). Для
этого в ней достаточно исключить резистор во втором контуре (
0
2
=R ) и
полученная схема становиться аналогичной схеме приведенной в
задаче 31 к данному параграфу. Проведите графические построения
самостоятельно, и убедитесь, что в первом контуре имеется три
резонанса: два последовательных и один параллельный расположенный
между ними. Поэтому амплитудно-частотная характеристика (АЧХ) тока
должна иметь два максимума на частоте последовательного резонанса и
минимум между
ними связанный с параллельным резонансом. Эти же
выводы можно сделать аналитически на основании полученного
выражения для входного сопротивления (4.50). Рассмотрим простой
случай:
0
2
=R
,
CCC
=
=
21
,
LLL
=
=
21
. Тогда
XXX =
=
21
и
)(
22
1
X
M
XjRZ
вх
ω
−+= . Из условия 0)Im(
вх
=
Z , которое выполняется
при
МX
ω
±
= , находим частоты последовательного резонанса:
kMCLC ±
=
±
=
1
1
0
2,1
ω
ω
, (4.51)
где введен коэффициент связи
/kML
=
и LC1
0
=
ω
. Тогда как, из
условия
∞=)Im(
вх
Z , что соответствует
0
=
X
, находим частоту
параллельного резонанса:
03
ω
ω
=
. При параллельном резонансе
100
амплитуда тока в первом контуре равна нулю, а во втором контуре
)()(
02
ρ
ω
kEI
m
=
, где CL=
ρ
и 0
≠
M . (При 0
=
M ток во втором
контуре тождественно равен нулю.) При последовательном резонансе эти
токи имеют равные амплитуды:
12,122,11
)()( REII
mm
==
ωω
. АЧХ тока
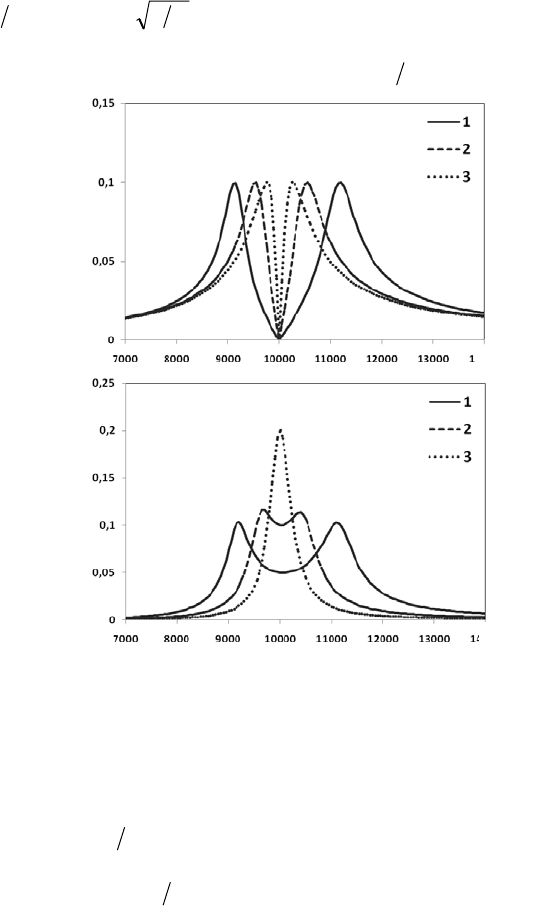
первого контура
имеет два резких
максимума положе-
ние, которых опре-
деляется коэффици-
ентом связи, чем он
больше, тем они
сильнее раздвига-
ются (рис. 4.15. а).
АЧХ тока второго
контура имеет бо-
лее сложную зави-
симость от коэффи-
циента связи. При
1
Rk >
ρ
АЧХ тока
так же имеет два
максимума на час-
тотах последова-
тельного резонанса.
Однако в данном
случае глубина про-
вала между ними
зависит от вели-
чины
ρ
k : с умень-
шением
ρ
k его
глубина уменьша-
ется, при
1
Rk ≅
ρ
он исчезает и далее
при
1
Rk <
ρ
в АЧХ проявляется только один максимум на частоте
параллельного резонанса (рис. 4.15, б). В связи с этим для связанных
контуров величина
)(
1
Rk
ρ
приобретает большое значение, и его
называют параметром или фактором связи. Фактор связи можно записать
как
kQ , где величина
1
RQ
ρ
=
соответствует добротности простого
Рис. 4.15. Амплитудно-частотные характеристики
токов в связанных контурах: а) ток первого кон-
тура; б) ток второго контура. Q = 10, R
1
=100 Oм,
Кривые: 1 – k = 0,2; 2 – k = 0,1; 1 – k = 0,05.
ω
,
c
-1
ω
,
c
-1
Ι
1
Ι
2
(a)
(б)
