Мищенко А.М. Сборник задач по линейным электрическим цепям с кратким изложением теории
Подождите немного. Документ загружается.

111
40.
В цепи катушки индуктивности включены согласно. При каком
значении сопротивления R
2
цепь будет находиться в состоянии резонанса
(напряжение и ток источника не сдвинуты по фазе)? Найти при этом
условии токи и потребляемые мощности в каждом контуре. E = 100 B,
1
L
X = 10 Ом,
2
L
X = 9 Ом,
C
X = 8 Ом,
M
X = 6 Ом.
41.
В цепи катушки индуктивности включены согласно,
10=E
B,
11
10 jXZ +=
[Ом],
50015
2
jZ
+
=
[Ом],
250=
M
X
Ом. При каком
значении реактивного сопротивления Х
1
цепь будет находиться в
состоянии первого частного резонанса? При этом резонансе ток во втором
контуре с увеличением частоты достигает свой первый максимум.
Определить при этом условии ток и потребляемую мощность во втором
контуре.
42.
В цепи задачи 37
10
=
E
B,
250
=
M
X
Ом,
11510
1
jZ
+
=
[Ом],
22
15 jXZ +=
[Ом]. При каком значении реактивного сопротивления Х
2
цепь будет находиться в состоянии второго частного резонанса? При этом
резонансе ток во втором контуре с увеличением частоты, пройдя первое
максимальное значение, достигает свой второй максимум. Определить
при этом условии ток и потребляемую мощность во втором контуре.
R
1
L
1
C
1
R
2
E
C
2
R
L
1
C
1
E
C
2
L
2
V
A
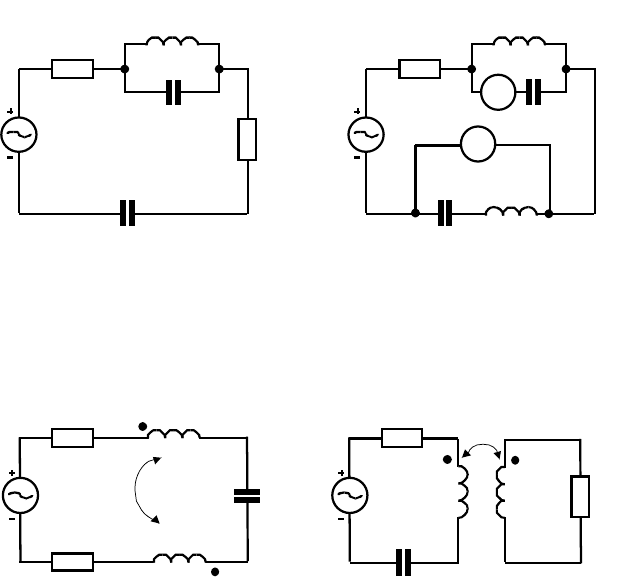
Рис. к задаче 37 Рис. к задаче 38
R
1
L
1
C
R
2
E
L
2
M
R
1
L
1
C
R
2
E
L
2
M
Рис. к задаче 39 Рис. к задаче 40
112
43.
В цепи задачи 37
10
=
E
B,
11
10 jXZ
+
=
[Ом],
27015
2
jZ +=
[Ом]. При каких значениях Х
1
и Х
М
цепь будет находиться
в состоянии полного резонанса? В этом случае ток во втором контуре
имеет один maximum maximorum. Определить при этом условии ток и
потребляемую мощность во втором контуре.
44.
В цепи L
1
= 4 Гн, L
2
= 2 Гн, С = 1 Ф, коэффициент связи
(
)(
22
LLMk
=
) равен
21
. Найти
резонансные частоты.
45.
В цепи E = 15 B, f = 0,8 кГц,
R
1
= R
2
= R = 200 Ом, L
1
= L
2
= L = 4 мГн,
С = 1 мкФ.
Как следует включить катушки (согласно
или встречно) для того, чтобы цепь
находилась в состоянии резонанса
(напряжение и ток источника в фазе)?
Найти при резонансе: токи в ветвях и
коэффициент связи (
)(
22
LLMk
=
).
R
1
L
1
C
1
R
2
E
L
2
M
C
2
L
1
E
L
2
M
C
R
Рис. к задаче 41 Рис. к задаче 44
C
E
M
L
1
R
2
L
2
R
1
М
Рис. к задаче 45
113
§ 5. Переходные процессы в электрических цепях
Переходные или нестационарные процессы возникают в результате
коммутаций и обеспечивают переход от одного стационарного режима к
новому. В электротехнике стационарный (установившийся) режим
называют принужденным, а под коммутацией понимают различные
включения, выключения, переключения пассивных и активных ветвей, а
также резкие изменения параметров элементов цепи. В
электротехнике
рассматриваются лишь квазистационарные переходные процессы, при
которых запасенная энергия магнитного и электрического поля изменяется
плавно, без скачков. Тем не менее, существуют особые случаи, когда при
коммутации в первые моменты времени возможны скачкообразные
изменения энергии в реактивных элементах цепи. В электротехнике эти
моменты времени, которые соизмеримы с Максвелловскими временами,
опускаются.
Законы коммутации и независимые начальные условия. Принци-
пы непрерывности потокосцепления и электрического заряда
В основе законов коммутации для реактивных элементов цепи:
индуктивности и емкости – лежит принцип непрерывности во времени
магнитного потока (потокосцепления) в индуктивности (L) и электри-
ческого заряда на емкости (С), т. е. принцип сохранения запасенной
энергии до и
после коммутации.
Первый закон коммутации гласит: в начальный момент после ком-
мутации ток в индуктивности остается таким же, каким он был
непосредственно перед коммутацией, а затем плавно изменяется. При
этом следует иметь в виду, что напряжение на индуктивности может
изменяться скачком.
Второй закон коммутации гласит: в начальный момент после
коммутации напряжение
на емкости остается таким же, каким оно
было непосредственно перед коммутацией, а затем плавно изменяется.
При этом также следует иметь в виду, что ток в емкости может изменяться
скачком.
На активном элементе – резисторе (R) ток и напряжение может изме-
няться скачком.
Ток в индуктивности и напряжение на емкости в момент
коммутации
называют независимыми начальными условиями. В математическом виде
их записывают в соответствие с основными законами коммутации
⎩
⎨
⎧
=+=−
=+=−
),()()(
),()()(
kCkCkC
kLkLkL
tututu
tititi
(5.1)
где t
k
– время момента коммутации; i
L
(-t
k
), u
C
(-t
k
) – ток в индуктивности и
напряжение на емкости до момента коммутации; i
L
(+t
k
), u
C
(+t
k
) –
114
соответственно после коммутации в первый момент переходного
процесса. Обычно за время отсчета берут момент коммутации, т. е.
полагают t
k
= 0.
Из условий (5.1) следует два важных частных случая:
• при
0)0( =−
L
i и 0)0(
=
−
C
u – индуктивность в момент коммутации
равносильна разрыву, а емкость – короткому замыканию;
• при
0
)0( ii
L
=− и
0
)0( uu
C
=
−
– индуктивность в момент коммутации
равносильна источнику тока с генерируемым током – i
0
, а емкость –
источнику напряжения с ЭДС, равной u
0
.
Для расчета переходного процесса обязательно требуется знание
независимых начальных условий, причем совершенно безразлично, каким
образом они возникли в цепи.
Отдельно необходимо рассматривать особые случаи, когда при
коммутации образуются: во-первых, контуры, состоящие либо из
источников ЭДС и конденсаторов, либо из одних конденсаторов
(сопротивление соединительных проводов пренебрежимо мало); во-
вторых, контуры
, состоящие из катушек индуктивности, причем катушки
индуктивности не зашунтированы резисторами, конденсаторами или
источниками напряжения. В таких контурах запасенная энергия
магнитного или электрического поля в первые моменты времени после
коммутации изменяется скачком и лишь затем, начинает плавно меняется.
В электротехнике эти моменты времени, связанные с быстро
протекающими процессами, опускаются и рассмотрение
переходного
процесса начинают после того как они закончатся. Для таких контуров
независимые начальные условия выводятся соответственно либо из
сохранения суммарного заряда на емкостях в контуре, либо из сохранения
общего магнитного потока (потокосцепления) контура. Прямое сле-
дование выше приведенным законам коммутации может привести к
противоречию с законами Кирхгофа.
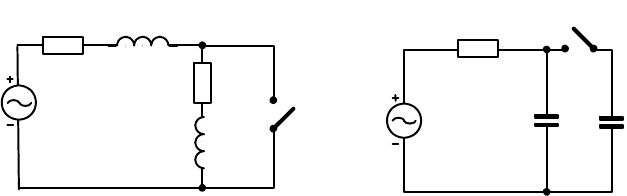
Проиллюстрируем возникновение данных особых
случаев на примере
двух цепей: одна с контуром имеющем две индуктивности (рис. 5.1);
L
1
R
1
R
2
L
2
K
e(t)
K
R
e(t) C
1
C
2
Рис. 5.1 Рис. 5.2

115
другая с контуром из двух емкостей (рис. 5.2). В первой цепи (рис. 5.1) при
замыкании ключа сохранение токов в индуктивностях после коммутации
не вызывает нарушение первого закона Кирхгофа. Поэтому независимые
начальные условия определяются первым равенством в выражении (5.1),
т. е.
)0()0(
11
+=−
LL
ii , )0()0(
22
+
=
−
LL
ii , где за время отсчета взят момент
коммутации. При размыкании ключа требование сохранения токов в
индуктивностях после коммутации вызывает нарушение первого закона
Кирхгофа. Поэтому в катушках должен произойти выравнивающий скачек
тока и в первые моменты времени после коммутации произойдет резкое
увеличение напряжений на индуктивностях. На практике это приводит к
пробою либо
в ключе, либо в катушках между витками. Теоретически без
учета пробоя найти данный скачёк тока можно с помощью уравнения,
записанном по второму закону Кирхгофа, оставив в нем только слагаемые
отвечающие за падения напряжения на индуктивностях:
0
21
21
≅+
dt
di
L
dt
di
L
LL
. За этот промежуток времени (τ) произойдет
перераспределение магнитных полей в катушках и токи в них станут рав-
ными (
)()()(
21
τ
τ
τ
LLL
iii =≅ ). Интегрируя уравнение Кирхгофа в интер-
вале от 0 до τ, получаем:
)()()0()0(
2121
21
τ
LLL
iLLiLiL
+
=
+
. Полученное
равенство можно трактовать, как сохранение магнитного потока в контуре
до и после коммутации. Отсюда, считая
0
≅
τ
, получаем независимое
начальное условие:
)/())0()0(()0(
2121
21
LLiLiLi
LLL
+
−
+
−
=
+ . Отметим,
что по окончании данного процесса часть энергии запасенной в катушках
индуктивности диссипируется.
Во второй цепи (рис. 5.2) при размыкании ключа в первый момент
времени заряды на конденсаторах остаются неизменными и независимые
начальные условия определяются вторым равенством в выражении (5.1).
Тогда как при замыкании ключа отсутствие между емкостями
сопротивления приводит к большим
токам, и заряды на емкостях
перераспределяются за малый промежуток времени. В электротехнике
этим временем пренебрегают и за время отсчета берут момент
коммутации. Используя условие сохранения суммарного заряда на
емкостях до и после коммутации, а также то, что после коммутации
напряжение на емкостях будет одинаковым, получается независимое
начальное условие:
)/())0()0(()0(
2121
21
CCuCuCu
CCC
+
−
+
−
=
+ . В этом
процессе часть энергии запасенной на конденсаторах диссипируется.
Расчет переходных процессов классическим методом
Анализ переходного процесса в разветвленной линейной цепи с
сосредоточенными параметрами (R, L, C ) классическим методом сводится
116
к решению задачи Коши для системы обыкновенных дифференциальных
уравнений (ОДУ), составленных на основании законов Кирхгофа для цепи
после коммутации. Начальными условиями для ОДУ служат значения
искомой функции (ток ветви или узловой потенциал) и величины ее
производных сразу после коммутации. Решение имеет вид суммы
свободной (решение однородной системы уравнений) и
принужденной
(частое решение) составляющей. Например, ток ветви
)()()( tititi
прсв
+
=
(5.2 а)
или узловой потенциал
)()()( tututu
прсв
+
=
(5.2 б)
Принужденные составляющие находят либо по установившемуся,
стационарному режиму работы схемы (любым способом, рассмотренным в
§ 3), либо прямым нахождением частного решения, применяя метод
вариации произвольных постоянных (метод Лагранжа) или метод Коши.
Для получения свободной составляющей систему ОДУ можно свести к
одному обыкновенному дифференциальному уравнению более высокого
порядка. Однако проще использовать операторный
метод, позволяющий
преобразовать исходную систему ОДУ в систему алгебраических
уравнений. С этой целью, производные d
k
/dt
k
заменяют на p
k
, а интегралы
либо исключают предварительным дифференцированием, либо заменяют
на 1/p. Тогда определитель системы дает характеристическое уравнение:
0)( =Δ p . Степень этого уравнения по отношению к оператору р
определяется количеством реактивных элементов. После этого находят
корни характеристического уравнения (р
k
), количество которых с учетом
кратности равно степени характеристического уравнения и записывают
решение системы ОДУ, придерживаясь общего правила.
Приведем в общем виде выражения для свободной составляющей на
примере тока ветви.
Для случая не кратных корней
,)(
1
∑
=
=
n
k
tp
kсв
k
eAti (5.3 а)
,)sin(
)sincos(
)()(
1
1
1
∑∑
∑∑
∑∑
=
−
=
=
−
=
−
==
−
++=
=++=
=++=
n
sk
kkk
t
sn
k
tp
k
n
sk
kkkk
t
sn
k
tp
k
sn
k
n
sk
tj
k
tj
k
ttp
kсв
tDeeA
tCtBeeA
eNeMeeAti
kk
kk
kkkk
ϕω
ωω
σ
σ
ωωσ
(5.3 б)
117
где n – степень характеристического уравнения; A
k
, B
k
, M
k
, N
k
, C
k
, D
k
, φ
k
–
постоянные интегрирования. В выражении (5.3 б) в явном виде показаны
комплексно сопряженные корни (p
k
= σ
k
± jω
k
).
Для случая кратных корней (кратностью m):
1) кратный корень – действительный (l–й корень)
,)(
,11
1
∑∑
−
≠==
−
+=
mn
lkk
m
k
k
k
tptp
kсв
tBeeAti
lk
(5.4)
2) кратный корень комплексно-сопряженный (l–й корень p
l
= σ
l
± jω
l
)
,)sin(
)()(
1
1
,1
,11
1
∑∑
∑∑
=
−
−
≠=
−
≠==
−
−
++=
=++=
m
k
klk
k
mn
lkk
ttp
k
mn
lkk
m
k
tj
k
tj
k
k
ttp
kсв
tDteeA
eNeMteeAti
lk
lllk
ψω
σ
ωωσ
(5.5)
где A
k
, B
k
, M
k
, N
k
, C
k
, D
k
, ψ
k
– постоянные интегрирования. Свободные
составляющие в цепях с пассивными элементами всегда затухают.
Поэтому действительные части всех корней должны быть отрицательны
(
σ
k
< 0).
Постоянные интегрирования находят из начальных условий.
Количество начальных условий должно быть равно количеству корней с
учетом их кратности. Поэтому кроме значений искомой функции в первый
момент после коммутации необходимо задать ее производные от первого
до n - 1 порядка. Начальные условия находят из законов коммутации и
уравнений Кирхгофа. С этой целью
удобно строить эквивалентную схему
для первых моментов, используя законы коммутации. В такой схеме
индуктивности заменяются идеальными источниками тока, емкости – на
идеальные источники напряжения. В частности, при нулевых начальных
условиях замена еще больше упрощает эквивалентную схему, так как в
этом случае индуктивность равносильна разрыву, а емкость – короткому
замыканию.
Суммируем основные этапы расчета
классическим методом:
1) рассчитывают токи в индуктивностях и напряжения на емкостях до
коммутации;
2) находят по законам коммутации токи в индуктивностях и
напряжения на емкостях после коммутации;
3) записывают систему дифференциальных уравнений на основе
законов Кирхгофа для схемы после коммутации;
4) находят начальные условия для токов или напряжений и их
производных по
п. 3 (часть начальных условий удобно находить из
эквивалентной схемы);

118
5) ищут частное решение системы неоднородных дифференциальных
уравнений п. 3 (установившиеся, стационарные токи или напряжения в
схеме после коммутации), т.е. принужденные составляющие;
6) находят решение системы однородных дифференциальных
уравнений, т. е. свободное решение (свободные составляющие);
7) определяют постоянные интегрирования решения п. 6;
8) находят окончательное решение сложением решений пп. 5, 6.
Основной объем расчетов
классическим методом связан, во-первых, с
нахождением корней (р
k
) характеристического уравнения, во-вторых, с
определением постоянных интегрирования по начальным условиям.
Расчет переходных процессов с применением преобразования
Лапласа
Расчет переходных процессов решением интегро-дифференциаль-
ных уравнений Кирхгофа методом преобразования Лапласа. Решение
интегро-дифференциальных систем уравнений данным методом основано
на возможности введения прямого и обратного преобразования функций
действительного переменного t в
область функций комплексного
переменного p = σ + jω.
Переход к функциям комплексного переменного осуществляют с
помощью прямого преобразования Лапласа
[]
)(
ˆ
)()(
0
tfLdtetfpF
pt
==
∫
∞
−
, (5.6)
где
L
ˆ
– оператор Лапласа. Строго говоря, преобразование определяет F(p)
в области значений p, для которых интеграл сходится, а именно в
полуплоскости σ > a, где a – абсцисса сходимости. В другой же
полуплоскости функция F(p) является аналитическим продолжением
интеграла (за исключением особых точек – полюсов).
При применении преобразования Лапласа к переходным процессам,
коммутацию
полагают при t = 0.
Определенную таким образом функцию F(p) называют изображением
по Лапласу, а функцию f(t) – оригиналом. Прямое преобразование первой
производной функции имеет вид
)0()(
)(
ˆ
+−=
⎥
⎦
⎤
⎢
⎣
⎡
fppF
dt
tdf
L , (5.7)
а интеграла –
p
pF
tdtfL
t
)(
)(
ˆ
0
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
′′
∫
, (5.8)

119
где F(p) – изображение по Лапласу функции f(t) а f(+0) – значение f(t) при
t = +0. Таким образом преобразование Лапласа переводит систему
интегро-дифференциальных уравнений в систему алгебраических
уравнений для изображений.
Обратное преобразование Лапласа осуществляют с помощью интеграла
[]
)(
ˆ
)(
2
1
)(
1
pFLdpepF
j
tf
jc
jc
pt
−
∞+
∞−
==
∫
π
, (5.9)
где c выбирается так, чтобы правее этой абсциссы отсутствовали полюсы
функции
)( pF
. При вычислении интеграла используют лемму Жордана,
заменяя путь интегрирования замкнутым контуром
n
Г
, составленным из
отрезка
(, )
nn
ajbajb−+ и части окружности
'
n
C , расположенной слева
от прямой
ap =Re . Это позволяет применять теорему о вычетах,
согласно которой оригиналом
)( pF служит функция:
pt
Г
p
n
epFrestf
n
k
)(lim)(
)(
∑
∞→
=
, (5.10)
где сумма берется по всем особым точкам функции
)( pF
, лежащей
внутри
n
Г
.
Обычно при расчете цепей изображение имеет вид правильной дроби
)(
)(
)(
2
1
pF
pF
pF =
. В отсутствии общих корней у числителя и знаменателя
полюсы изображения определяется корнями уравнения
0)(
2
=pF .
Возможны два случая: а) все корни простые; б) некоторые или все корни
кратные.
В случае простых корней расчет оригинала проводят по формуле
,
)(
)(
)(
)(
)(
)(
)(
)(
)(
ˆ
)(
1
2
1
1
2
1
1
2
1
2
1
1
∑∑
∑
==
=
=
−
′
=
⎥
⎦
⎤
⎢
⎣
⎡
−=
==
⎥
⎦
⎤
⎢
⎣
⎡
=
n
k
tp
k
k
n
k
pp
pt
k
n
k
pt
p
k
k
k
e
pF
pF
e
pF
pF
pp
e
pF
pF
res
pF
pF
Ltf
(5.11)
где сумма берется по всем n корням
)(
2
pF
,
k
pp
dp
pdF
pF
=
=
′
)(
)(
2
2
.
Для случая кратных корней приведем формулу расчета оригинала для
ситуации, когда l-й корень имеет кратность m:

120
.}
)(
)(
){(
)!1(
1
)(
)(
)(
)(
)(
)(
)(
)(
)(
)(
)(
ˆ
)(
2
1
1
1
1
2
1
2
1
1
2
1
1
2
1
2
1
1
l
k
lk
k
pp
ptm
l
m
m
mn
k
pp
pt
k
pt
p
mn
k
pt
p
n
k
pt
p
e
pF
pF
pp
dp
d
m
e
pF
pF
ppe
pF
pF
rese
pF
pF
res
e
pF
pF
res
pF
pF
Ltf
=
−
−
−
=
=
−
=
=
−
⎥
⎦
⎤
⎢
⎣
⎡
−
−
+
+
⎥
⎦
⎤
⎢
⎣
⎡
−=+=
==
⎥
⎦
⎤
⎢
⎣
⎡
=
∑∑
∑
(5.12)
Суммирование по всем корням проводиться после сокращения на (p – p
k
),
а дифференцирование после сокращения на (p – p
k
)
m
. В окончательные
выражения подставляют соответствующие значения корня.
Для достаточно широкого класса функций существуют таблицы
оригиналов и изображений (Приложение 2), которые упрощают взаимные
переходы от изображений к оригиналам и наоборот.
Расчет переходных процессов с применением преобразования Лапласа
сводится к следующей последовательности действий:
1) записывают уравнения Кирхгофа в интегро-дифференциальной
форме с учетом независимых
начальных условий (начальных токов в
индуктивностях и начальных напряжений на емкостях);
2) применяя преобразование Лапласа, переходят к алгебраическим
уравнениям для изображений токов и напряжений;
3) решают полученные алгебраические уравнения;
4) применяя обратное преобразование Лапласа, находят оригиналы,
т. е. искомые функции тока или узлового потенциала.
Использование преобразований Лапласа является лишь матема-
тическим методом
решения уравнений Кирхгофа. По сравнению с
классическим методом он упрощает проведение расчетов переходных
процессов, так как не требует нахождения: во-первых, всех начальных
условий (производных от первого до n
- 1 порядка); во-вторых, частного
решения для установившегося процесса; и, в-третьих, постоянных
интегрирования. Однако эта простота обеспечивается лишь возможностью
использования таблиц оригиналов и изображений, приводимых в
математических справочниках. Нахождение полюсов требует решение
уравнений аналогичных характеристическим уравнениям в классическом
методе. Поэтому здесь также могут возникнуть уравнения третьего и более
порядка, решение которого
в аналитическом виде не всегда возможно.
Расчет переходных процессов операторным методом. Операторный
метод основан на свойствах преобразования Лапласа (выражения (5.7)–
(5.8)), которые позволяют заменить исходную схему эквивалентной
