Мищенко А.М. Сборник задач по линейным электрическим цепям с кратким изложением теории
Подождите немного. Документ загружается.

121
схемой изображений. Построение эквивалентной схемы сводится к
следующей последовательности действий.
1)
Все реальные источники тока и напряжения заменяют изобра-
жениями.
2)
Индуктивности в силу свойства дифференцирования оригинала
[]
)0()(
)(
ˆ
)(
ˆ
+−=
⎥
⎦
⎤
⎢
⎣
⎡
=
L
L
L
LippLI
dt
tdi
LLtuL
(5.13)
заменяют не только на эффективное сопротивление pL, но и
последовательно с ним в схему вводят идеальный источник напряжения с
ЭДС, равной L⋅i
L
(+0), где i
L
(+0) – ток в индуктивности в момент
коммутации. Знак ЭДС совпадает с выбранным направлением тока в
индуктивности.
3)
Емкость, имеющую начальное напряжение u
C
(+0), в силу свойства
интегрирования оригинала
[]
p
u
pC
pI
utdti
C
LtuL
C
t
CC
)0()(
)0()(
1
ˆ
)(
ˆ
0
+
+=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
++
′′
=
∫
(5.14)
заменяют не только на эффективное сопротивление –
pC1 , но и
последовательно с ним вводят идеальный источник напряжения с ЭДС,
равной
(0)/
C
up+ . Направление ЭДС в этом случае противоположно
выбранному направлению тока в емкости.
Эффективные сопротивления по виду аналогичны соответствующим
комплексным сопротивлениям индуктивностей и емкостей в цепях
синусоидального тока, рассчитываемых методом комплексных амплитуд.
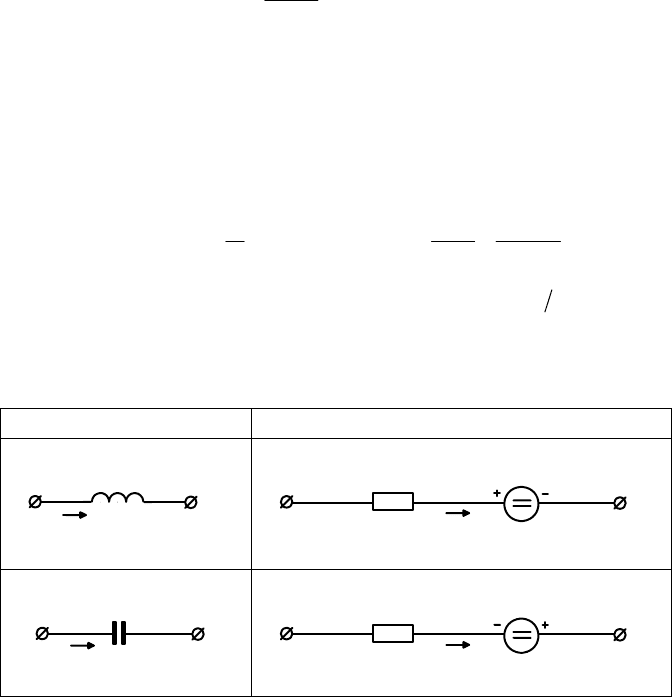
Исходная схема Операторная схема
L
u
1
(t)
i(t)
u
2
(t)
Z(p)=pL
Li
L
(+0)
U
1
(p)
I(p)
U
2
(p)
C
u
1
(t)
i(t)
u
2
(t)
Z(p)=1/pC
u
C
(+0)/p
U
1
(p)
I(p)
U
2
(p)
Рис. 5.1
122
Только в данном случае вместо
ω
j стоит p. На рис. 5.1 приведены такие
эквивалентные операторные схемы индуктивности и емкости.
Операторные схемы на рис. 5.1 можно рассматривать как схемы
источников напряжения с внутренними сопротивлениями. Тогда,
используя правило эквивалентности источников напряжения и источников
тока, рассмотренное в § 1, индуктивность и емкость в схемах изображений
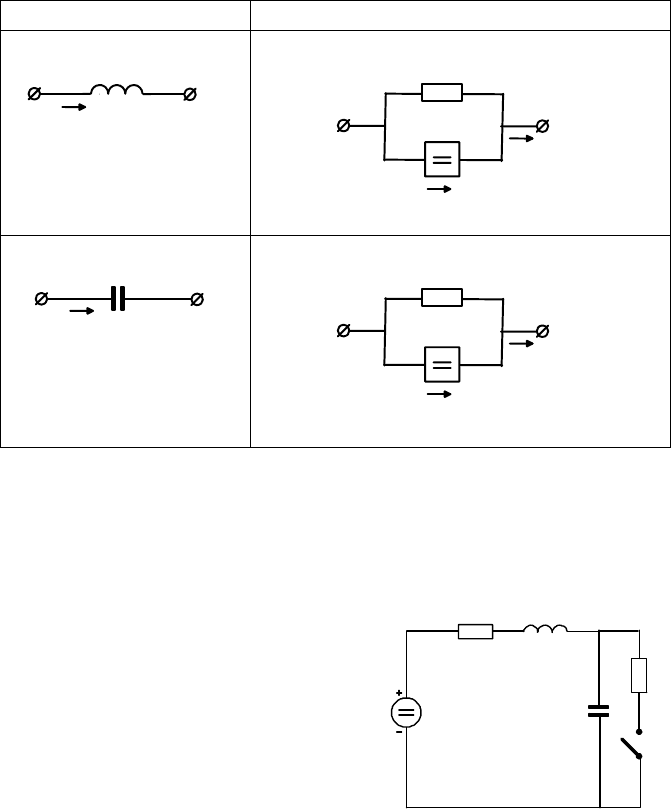
можно представлять и операторными схемами источника тока (рис. 5.2).
При этом не надо забывать, что эквивалентность замены операторной
схемы источника напряжения на операторную схему источника тока
осуществляется по отношению к внешней цепи (см. § 1).
Операторный метод в отличие от
прямого применения преобразований
Лапласа к уравнениям Кирхгофа
позволяет с помощью эквивалентных
операторных схем непосредственно
использовать все методы развитые для
расчета цепей синусоидального
тока
(см. § 3).
Пример 1. Расчет переходных
процессов классическим методом.
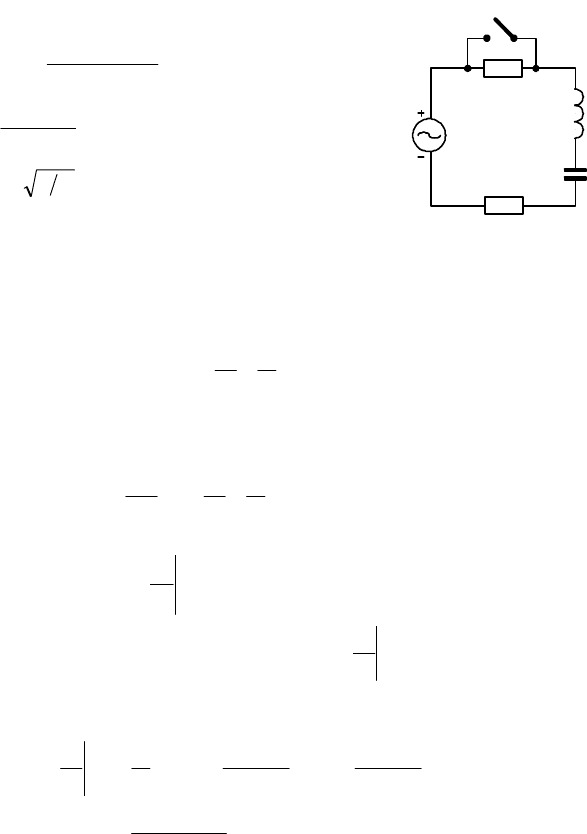
Найдем ток в цепи, показанной на
Исходная схема Операторная схема
L
u
1
(t)
i(t)
u
2
(t)
Z(p)=pL
I(p)
i
L
(+0)/p
U
1
(p)
U
2
(p)
C
u
1
(t)
i(t)
u
2
(t)
Z(p)=1/pC
I(p)
Cu
C
(+0)
U
1
(p)
U
2
(p)
Рис. 5.2
R
2
L
R
1
E
K
Рис.5. 3
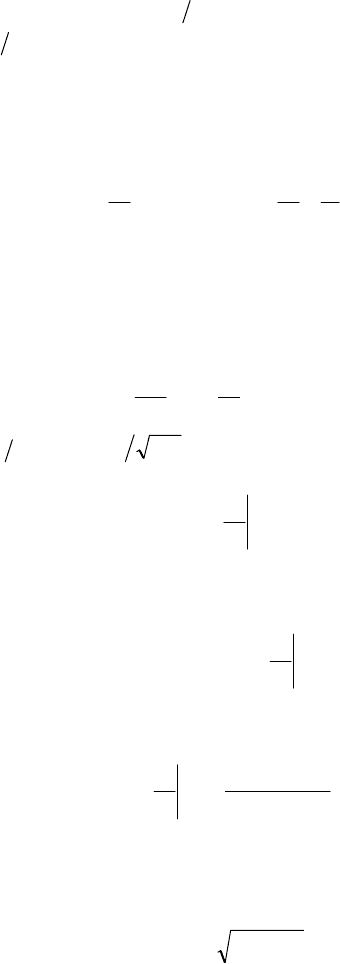
123
рис. 5.3, после размыкания ключа. До размыкания ключа напряжение на
конденсаторе
)()0(
212
RRERu
+
=− ; ток в индуктивности
)()0(
21
RREi +=− . Из законов коммутации следуют независимые
начальные условия
0
)0()0( iii
L
=
−
= ,
0
)0()0( uuu
CC
=
−
=
.
При размыкании ключа конденсатор начнет перезаряжаться до тех пор,
пока напряжение на нем не установиться равным
Е
. Уравнение Кирхгофа
для цепи после коммутации
0
0
')'(
1
)( udtti
Cdt
di
LRitu
dt
di
LRiE
t
C
+++=++=
∫
. (5.15)
Решение этого уравнения можно проводить операторным методом,
заменяя производную p, а интеграл на 1/p, или методом исключения
интеграла дифференцированием уравнения по времени. Выберем второй
метод. Тогда уравнение (5.15) сведётся к однородному диф-
ференциальному уравнению второго порядка:
02
2
0
2
2
=++ i
dt
di
dt
id
ωβ
, (5.16)
где
)2( LR=
β
, LC1
0
=
ω
. Решение уравнения (5.16) является током
контура в переходном процессе. Для решения его недостает начального
условия на производную тока
0=t
dt
di
, так называемого зависимого
начального условия. Это условие получим непосредственно из уравнения
Кирхгофа (5.15), которое надо записать для первого момента после
коммутации, используя известный начальный ток:
0
00
=
++=
t
dt
di
LRiuE
. (5.17)
Тогда полная система начальных условий:
⎪
⎩
⎪
⎨
⎧
−−
=
=
=
.
,0)0(
00
0
L
RiuE
dt
di
i
t
(5.18)
Характеристическое уравнение дифференциального уравнения (5.16)
02
2
0
2
=++
ωβ
pp . (5.19)
Оно имеет общее решение
2
0
2
2,1
ωββ
−±−=p . (5.20)
124
Отсюда решение однородного уравнения (5.16), в предположении
21
pp ≠
(корни не кратные):
tptp
eCeCti
21
21
)( += . (5.21)
При
0
ω
β
< корни характеристического уравнения являются комп-
лексно-сопряженными
22
02,1
βωβ
−±−= jp и в контуре возникают
затухающие колебания с частотой
2
0
22
0
)2(11 Q
с
−=−=
ωβωω
.
Если добротность контура Q велика, то
c
ω
ω
≈
0
. При
0
ω
β
> в
переходном процессе отсутствуют колебания и процесс протекает с
плавным затуханием тока (апериодические колебания). Будем
предполагать, что в контуре реализуется первый случай. Тогда, используя
начальные условия (5.18), получаем систему уравнений для определения
постоянных интегрирования:
⎪
⎩
⎪
⎨
⎧
−−
=+
=+
.
,
00
2211
021
L
RiuE
CpCp
iCC
(5.22)
Решение системы дает:
.
2
2/
2
1
,
2
1
2
2/
00
020
00
1
Lj
RiuE
iCi
Lj
RiuE
C
cc
ωω
−−
−=+
−−
=
(5.23)
Подставляя найденные значения
1
С
и
2
С
в равенство (5.21) и используя
формулы
j
ee
t
tjtj
c
cc
2
)sin(
ωω
ω
−
−
=
,
2
)cos(
tjtj
c
cc
ee
t
ωω
ω
−
+
=
,
получаем искомый ток в цепи после коммутации
)cos()sin(
2/
)(
0
00
teite
L
RiuE
ti
c
t
c
t
c
ωω
ω
ββ
−−
+
−−
= . (5.24)
Пример 2. Расчет переходных процессов классическим методом. На
рис. 5.4 приведена схема с синусоидальным источником напряжения
)sin()(
0
ϕ
ω
+= tEte . Источник напряжения работает на резонансной
частоте
LC1
0
=
ω
. Найдем ток i(t) в цепи после замыкания ключа.
До момента коммутации при t = 0 ток в индуктивности
)sin()0(
2
1
ϕ
RR
E
i
L
+
=−
, (5.25)
125
а напряжение на емкости
),cos(
)(
)cos(
)(
)0(
0
21
0
210
ϕω
ρ
ϕω
ω
+
+
−=
=+
+
−=−
t
RR
E
t
CRR
E
u
C
(5.26)
где
CL=
ρ
, а величина
ϕ
соответствует
фазе напряжения источника в момент ком-
мутации. Используя законы коммутации,
получаем независимые начальные условия:
)0()0(
−
=
L
ii
и
)0()0(
−
=
CC
uu
.
Уравнение Кирхгофа для цепи после коммутации
∫
+++=
t
C
uidt
Cdt
di
LiRte
0
2
)0(
1
)( (5.27)
Дифференцируя его, получаем дифференциальное уравнение второго
порядка, причем в отличие от примера 1, здесь уравнение неоднородное:
)cos(
1
002
2
2
ϕωω
+=++ tEi
Cdt
di
R
dt
id
L
. (5.28)
Начальными условиями для этого уравнения являются: 1) тока i(0) и
2) первая производная
0=t
dt
di
в первый момент после коммутации. Ток i(0)
уже найден. Значение же первой производной
0=t
dt
di
(зависимое начальное
условие) найдем из уравнения Кирхгофа (5.27), записав его для первого
момента после коммутации и использовав i(0), u
C
(0),
).cossin(
)(
)cossin(sin
1
21
2121
2
0
ϕρϕ
ϕ
ρ
ϕϕ
+
+
=
=
+
+
+
−=
=
R
RRL
E
RRRR
R
L
E
dt
di
t
(5.29)
Решение уравнения (5.28) начнем с поиска частного решения, которое
одновременно является принужденным и установившимся током. Найдем
его как установившийся в цепи ток, используя метод комплексных
амплитуд. Наличие резонанса в цепи после замыкания ключа позволяет
сразу записать:
Рис.5. 4
e(t)
C
L
R
2
R
1
K
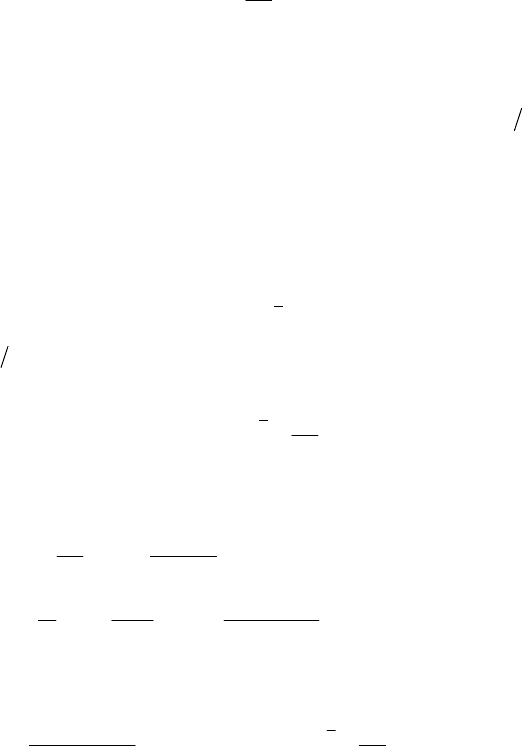
126
)sin()()(
0
2
ϕω
+== t
R
E
titi
пруст
. (5.30)
Теперь найдем общее решение однородного дифференциального
уравнения, которое является свободным током (i
св.
). Для его нахождения
необходимо сначала решить характеристическое уравнение, которое
аналогично уравнению (5.19). Однако в данном случае
)2(
2
LR
=
β
.
Поэтому переходной процесс может и здесь в зависимости от знака
дискриминанта развиваться по затухающему процессу с и без
периодических колебаний. В этом примере будем полагать, что
переходный процесс идет без колебаний и дискриминант равен нулю, т. е.
ρ
2
2
=R
. Тогда решение однородного дифференциального уравнения, а,
следовательно, и свободный ток
τ
t
св
eBtAi
−
+= )( , (5.31)
где
β
τ
1=
.
Реальный ток в цепи является суммой найденных токов:
)sin()()(
0
2
ϕω
τ
+++=+=
−
t
R
E
eBtAiiti
t
устсв
. (5.32)
Используя начальные условия для реального тока, получаем систему
уравнений для нахождения констант А и В:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+
+
=++−
+
=+
).cossin(
)(
cos
,sinsin
1
212
0
212
ϕρϕϕ
ω
τ
ϕϕ
R
RRL
E
R
E
B
A
RR
E
R
E
A
(5.33)
Подставляя решения системы (5.33) в выражение (3.32) для реального
тока, получаем искомый ток
[]
)sin(1)(
)(
sin
)(
0
2
0
1
212
1
ϕωϕωτ
ϕ
τ
++−−
+
=
−
−
t
R
E
ectgt
RRR
ER
ti
t
(5.34)
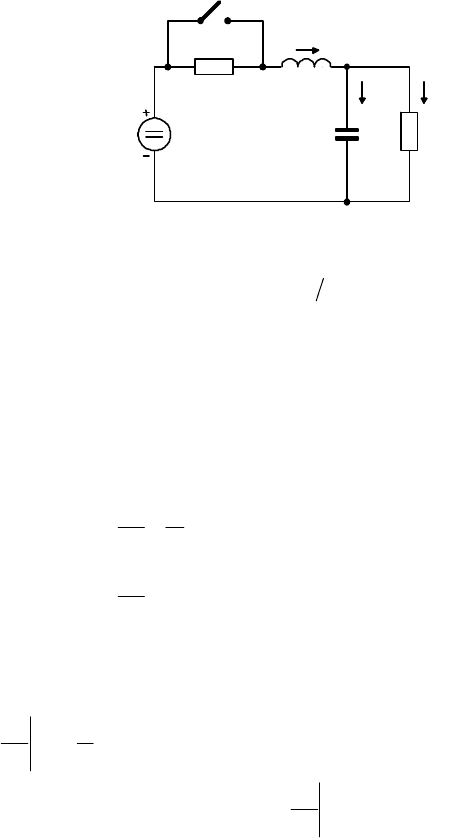
Пример 3. Расчет переходных процессов классическим методом.
Переходной процесс в схеме, изображенной на рис. 5.5, возникает после
размыкания ключа. Расчеты проведем в несколько этапов. В начале
найдем токи общим способом, используя полную систему уравнений
Кирхгофа. Затем для сравнения найдем токи, используя метод контурных
токов и наконец рассчитаем напряжение на конденсаторе. При этом в силу
громоздкости выражений ограничимся демонстрацией основных этапов
расчета и выделением достоинств того или иного метода. Полученные
127
результаты могут, без труда,
продолжены с использова-
нием конкретных значений
параметров схемы.
Нахождение токов вет-
вей методом Кирхгофа.
Расчеты начтем с устано-
вления независимых началь-
ных условий. Постоянный ток
не проходит через конден-
сатор, а индуктивность не
оказывает ему сопротивле-
ния. Поэтому до момента коммутации (t = 0)
2
)0( REi
L
=
, Eu
C
=)0( .
После коммутации эти значения сохраняются и являются независимыми
начальными условиями.
Система уравнений Кирхгофа после коммутации, где в качестве
независимых контуров выбран контур содержащий источник и
конденсатор, и контур содержащий источник и резистор
2
R :
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
++=
+
′′
++=
+=
∫
,
),0()(
1
,
22
1
11
0
3
1
11
321
iR
dt
di
LiRE
utdti
Cdt
di
LiRE
iii
t
C
(5.35)
где токи i
1
, i
2
и i
3
– в сопротивлениях
1
R ,
2
R и емкости.
Найдем зависимые начальные условия, используя эту систему и
независимые начальные условия. Из второго уравнения получаем
))0()0((
1
11
0
1
C
t
uiRE
Ldt
di
−−=
=
. (5.36)
Из третьего уравнения системы и найденное значение
0
1
=t
dt
di
получаем
222
//)0()0( RERui
C
=
=
. (5.37)
Отметим, что условие (5.37) можно найти и проще воспользовавшись
равенством напряжений на емкости и на сопротивлении R
2
. Это бы
следовало автоматически из системы уравнений Кирхгофа, если бы в
качестве второго контура был выбран контур из конденсатора и резистора
Рис.5. 5
E
K
L
C R
2
i
1
i
3
i
2
R
1

128
2
R . Из первого уравнения системы, используя независимое условие на ток
в индуктивности и найденный ток i
2
(0), получаем
0)0(
3
=
i . (5.38)
Значение
0
2
=t
dt
di
найдем путем вычитания третьего уравнения системы из
второго с последующим дифференцированием:
0
)0(
2
3
0
2
==
=
CR
i
dt
di
t
. (5.39)
Наконец, дифференцируя первое уравнение, находим
0
2
0
1
0
3
==
=
−=
tt
t
dt
di
dt
di
dt
di
. (5.40)
Найдем частное решение системы уравнений Кирхгофа, соот-
ветствующее установившемуся, стационарному состоянию схемы после
коммутации или принужденному режиму. Постоянный ток через емкость
не проходит, поэтому
0
пр3
=
i и )/(
21пр2пр1
RREii
+
=
=
.
Заменяя
dt
d
на р и
∫
t
0
на
p
1
, получим характеристическое уравнение
системы (5.35)
0)()(
2121
2
2
=++++ RRpLRCRpCLR (5.41)
из условия равенства нулю определителя её матрицы
0
111
0
1
0
21
1
=
−−
+
+
RLpR
Cp
LpR
. (5.42)
После нахождения корней характеристического уравнения (p
1,2
) можно
записать решение однородной системы (свободные составляющие токов) в
общем виде, полагая, что корни различны
⎪
⎩
⎪
⎨
⎧
+=
+=
+=
.)(
,)(
,)(
21
21
21
653
432
211
tptp
св
tptp
св
tptp
св
eCeCti
eCeCti
eCeCti
(5.43)
Теперь можно записать в общем виде и полное решение системы
129
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=+=
+++=+=
+++=+=
.)()()(
),/()()()(
),/()()()(
21
21
21
65333
2143222
2121111
tptp
прсв
tptp
прсв
tptp
прсв
eCeCtititi
RREeCeCtititi
RREeCeCtititi
(5.44)
Окончательное решение получается после нахождения постоянных
интегрирования по найденным начальным условиям.
Рассмотренный общий подход не всегда целесообразен. Особенно если
необходимо найти зависимость только одной неизвестной. В этом случае
бывает проще последовательным исключением неизвестных свести
систему уравнений Кирхгофа к одному дифференциальному уравнению
более высокого порядка. Например, для нахождения i
1
последовательная
подстановка i
2
из первого уравнения в третье, а затем i
3
во второе дает
уравнение второго порядка
EiRR
dt
di
LRCR
dt
id
RLC =++++⋅⋅
121
1
21
2
1
2
2
)()( . (5.45)
Начальные условия:
)0(
1
i и
0
1
=t
dt
di
находятся также как и раньше.
Нахождение токов ветвей методом контурных токов. В данной цепи
два независимых контура. Пусть первый контур состоит из ветвей с
источником и емкостью, а второй из ветвей с емкостью и сопротивлением
R
2
. Тогда система уравнений для контурных токов имеет вид
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+
′′
−
′
+=
+
′′
−
′
++=
∫
∫
),0())()((
1
0
),0())()((
1
t
0
1222
t
0
21
1
11
C
C
utdtItI
C
IR
utdtItI
Cdt
dI
LIRE
(5.46)
а её начальные условия
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
−=
−−=
=
=
=
=
)./()/)0(/(
,/))0()0((
,)0()0(
,)0(
222
0
2
11
0
1
22
21
CRRuRE
dt
dI
LuIRE
dt
dI
RuI
REI
C
t
C
t
C
(5.47)

130
Первые два начальных условия получены из независимых условий, а
последние (зависимые условия) из системы уравнений (5.46) с
использованием первых. Решение этой система проводиться одним из
выше изложенных способов. По найденным контурным токам отыскивают
все физические токи. Данный способ имеет преимущество в получении
системы уравнений с меньшим количеством уравнений.
Непосредственное применение
метода узловых потенциалов для
нахождения переходных процессов классическим методом невозможно,
когда ветви состоят из нескольких элементов. Поэтому нахождение
узловых потенциалов приходиться определять по найденным токам. Этот
процесс достаточно сложен, так как при наличии конденсаторов
необходимо интегрировать достаточно громоздкие выражения. Для
определения напряжений более предпочтительны методы основанные на
преобразованиях Лапласа. Тем не
менее, в отдельных случаях можно сразу
найти узловые потенциалы классическим методом без предварительного
поиска токов ветвей.
Проиллюстрируем это на рассматриваемом примере. В схеме на
рис. 5.5 конденсатор образует ветвь, поэтому, приравнивая нулю
потенциал нижнего узла, напряжение верхнего узла является напряжением
на конденсаторе. Это позволяет выразить токи i
2
и i
3
через напряжение на
конденсаторе:
22
Rui
C
= , dtduCi
C
=
3
. Далее используя первый закон
Кирхгофа для верхнего узла (первое уравнение в системе(5.35)) получаем:
dtduCRui
CC
+
=
21
. (5.48)
Теперь записывая закон Кирхгофа для контура с источником и
конденсатором (второе уравнение в системе (5.35)) с использованием
выражения (5.48), получаем дифференциальное уравнение второго
порядка
C
CC
u
R
R
dt
du
R
L
CR
td
ud
LCE )1()(
2
1
2
1
2
2
++++= (5.49)
с начальными условиями
⎪
⎩
⎪
⎨
⎧
−=−=
=
=
.
)0(
)0(
1
,)0(
222
1
0
CR
E
CR
E
CR
u
i
Cdt
du
Eu
C
t
C
C
(5.50)
Последнее условие получено с использованием равенства (5.48) и
знания тока в индуктивности до коммутации. Решение уравнения (5.48)
проводиться обычным способом.
Пример 4. Расчет переходных процессов с использованием преобра-
зования Лапласа. Расчет проведем для случая примера 2, чтобы можно
было провести сравнение с ранее проведенным расчетом классическим
Рис.
5.3.1
