Мищенко А.М. Сборник задач по линейным электрическим цепям с кратким изложением теории
Подождите немного. Документ загружается.

141
34.
В цепи в момент t = 0 замыкается ключ. ЭДС генератора
напряжения изменяется по закону
at
Atete
−
=)( . Определить напряжение
на конденсаторе.
35.
В цепи источник постоянного тока с I
0
=2 А включается в момент
t = 0. Напряжение на сопротивлении при t > 0 имеет зависимость от
времени:
)(6)(
62 tt
eetu
−−
−= [В]. Найти R, L, C.
36.
В цепи E = 12 B в момент t = 0 замыкают ключ и при t > 0 в ветви
сопротивления R
3
ток
t5,1
3
e24)t(i
−
+= [А]. Найти в схеме значения
сопротивлений и индуктивности.
37.
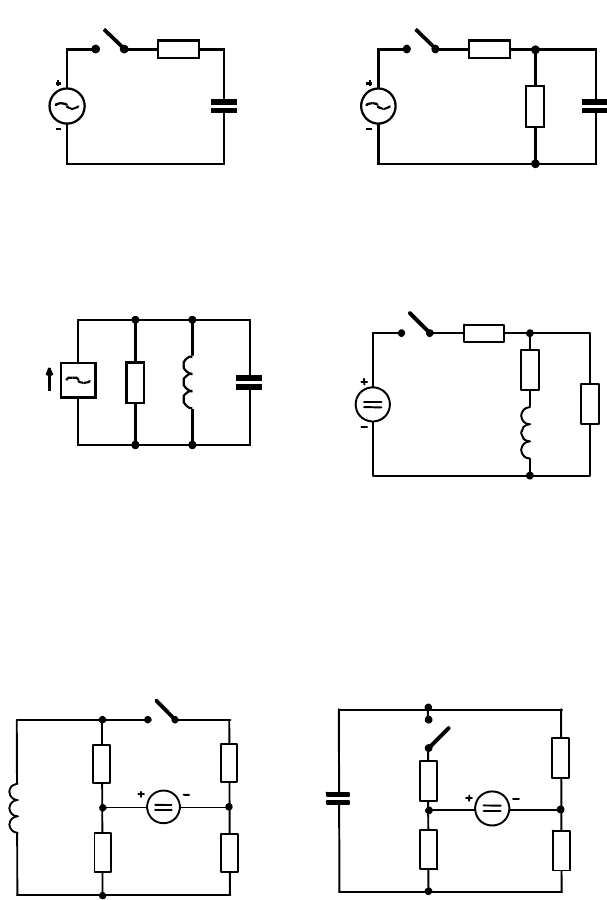
Найти ток в индуктивности после замыкания ключа.
38.
Найти напряжение на емкости после замыкания ключа.
K
C
R
e(t)
K
R
2
C
R
1
e(t)
Рис. к задаче 33 Рис. к задаче 34
R
L
Ci
0
(t)
R
3
R
2
R
1
K
E
L
Рис. к задаче 35 Рис. к задаче 36
R
1
R
2
R
4
K
L
E
R
3
R
1
R
2
R
4
K
С
E
R
3
Рис. к задаче 37 Рис. к задаче 38
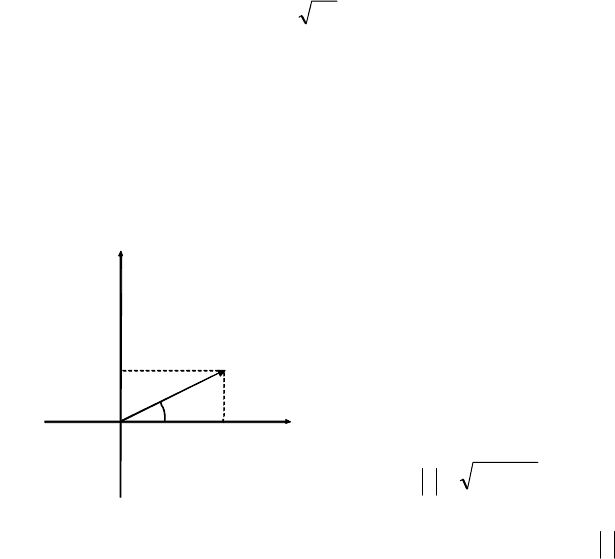
142
Приложение 1.
Комплексные числа и основные операции над ними
Комплексным числом z называется выражение вида
jbaz
+
=
, (П1.1)
где a, b – действительные числа, называемые вещественной и мнимой
чатями комплексного числа, 1−=j - мнимая единица. Вещественную и
мнимую части можно записывать еще и так:
)Re(za
=
, )Im(zb = .
Выражение (П1.1) – это алгебраическая форма записи комплексного
числа.
Комплексное число z отображается на комплексной плоскости точкой
z(a,b), абсцисса которой равна a, а ордината – b. Ось абсцисс, на которой
откладывается вещественная часть комплексного числа, называется
действительной (Re), а ось ординат на которой откладываться мнимая
часть, - мнимой (Im). Это позволяет комплексное число понимать
как
вектор 0Z с началом в точке 0(00) (начало координат) и с концом в точке
z(a,b) (рис. П1.1). Точке 0(00)
соответствует нулевой вектор.
Длина вектора, изображающего
комплексное число, называется
модулем этого числа и в соот-
ветствии с теоремой Пифагора
определяется через его действи-
тельную и мнимую части
формулой
22
baz += . (П1.2)
Комплексные числа z, имею-
щие один и тот же модуль
rz = ,
соответствуют точкам комплексной плоскости на окружности радиуса r с
центром в начале координат. Модуль равный нулю имеет только одно
комплексное число:
0=z
(
0
=
a
и
0
=
b
).
Направление вектора z углом φ, образуемый данным вектором с
положительным направлением вещественной оси. Этот угол называется
аргументом комплексного числа. Положительное направление отсчета
угла – против часовой стрелки от оси абсцисс. Задание модуля и аргумента
комплексное число определяется однозначно. Только число
0
=
z задается
одним модулем, для него аргумент не определяется. Аргумент
комплексного числа, в отличие от модуля, определяется не однозначно.
Множество его значений отличаются друг от друга на 2πk, где k – целое
Z
φ
Im(Z)
Re(Z)
a
b
Рис. П1.1
143
число. Главное значение аргумента заключено в промежутке
π
ϕ
π
≤
≤
−
.
Вещественная и мнимая части комплексного числа есть проекции
вектора z на действительную и мнимую оси (рис. П1.1):
ϕ
cos)Re( zza == , (П1.3а)
ϕ
sin)Im( zzb == . (П1.3б)
Главное значение аргумента комплексного числа можно найти как
a
b
arktg=
ϕ
. (П1.4)
Используя выражения (П1.1) и (П1.3), комплексное число можно
записать в тригонометрической форме:
ϕϕ
sincos zjzz += . (П1.5)
Используя формулу Эйлера
ϕϕ
ϕ
sincos je
j
+= , (П1.6)
где
e - основание натурального логарифма, переходим от тригономет-
рической формы записи комплексного числа к показательной форме
ϕ
j
ezz = . (П1.7)
Равенство комплексных чисел
ϕ
j
ezjbaz =+= и
1
1111
ϕ
j
ezjbaz =+=
обеспечивается равенством их действительных и
мнимых частуй:
1
aa =
,
1
bb
=
. Равнозначно, два комплексных числа z и
1
z равны, если равны их модули
1
zz = , а аргументы отличаются на 2πk
(k – целое число):
k
π
ϕ
ϕ
2
1
±= .
Комплексные числа
ϕ
j
ezjbaz =+=
и
ϕ
j
ezjbaz
−∗
=−=
называются сопряженными если отличаются только знаком мнимой части.
Модули сопряженных чисел равны, а главные значения аргументов
отличаются только знаком. На комплексной плоскости точки
соответствующие комплексным числам симметричны относительно
действительной оси.
Понятия «больше» и «меньше» для комплексных чисел не существует.
Арифметические действия с комплексными числами выполняются так
же, как
с обычными двучленами, учитывая, что 1
2
−=j .
Операции сложения и вычитания наиболее удобно проводить,
используя алгебраическую форму записи
144
)()()()(
11111
bbjaajbajbazz
+
+
+
=
+
+
+=+
, (П1.8)
)()()()(
11111
bbjaajbajbazz
−
+
−
=
+
−
+=−
. (П1.9)
В частном случае, сумма двух сопряженных чисел
jbaz +
=
и
jbaz −=
∗
есть действительное число равное a2 .
Умножение, деление и возведение в степень комплексных чисел
наиболее удобно проводить в показательной форме:
)(
111
][
1
ϕϕ
ϕ
ϕ
+
==
j
j
j
ezzezezzz , (П1.9)
)(
1
1
1
1
1
ϕϕ
ϕ
ϕ
−
==
j
j
j
e
z
z
ez
ez
z
z
, (П1.10)
ϕϕ
jn
n
njn
ezezz == ][ . (П1.11)
Частные случаи. 1) Умножение комплексного числа на действительное
число
c приводит к увеличению его модуля в c раз. В векторном смысле
это означает увеличение длинны исходного вектора в
c раз:
ϕ
j
ezccz = .
2) Для поворота вектора
ϕ
j
ezz = на заданный угол ψ необходимо
умножить его на единичный вектор
ψ
j
e :
)(
ψϕψ
+
=
jj
ezze Для поворота
против часовой стрелки знак ψ должен быть положительным, а для
поворота по часовой стрелки – отрицательным. В частности, умножение
вектора на
1
−
, означает изменение его направления на противоположное
или его поворот на
π
± : Это следует из равенства
π
j
e
±
=−1 . Умножение
на
j± приводит к повороту вектора на
2
π
± . Знака «+ » для поворота
против часовой стрелки и знак «−» - по часовой стрелке. Это следует из
равенства
2
π
j
ej
±
=± .
3) Умножение сопряженных комплексных чисел равно квадрату их
модулей:
2
zezezzz
jj
==
−∗
ϕϕ
.
Умножение и деление комплексных чисел в алгебраической форме:
)()())((
1111111
abbajbbaajbajbazz
+
+
−
=
+
+=
, (П1.12)
145
.
)()(
))((
))((
2
1
11
2
1
11
2
1
2
1
1111
1111
11
111
z
abba
j
z
bbaa
ba
abbajbbaa
jbajba
jbajba
jba
jba
z
z
+
+
−
=
=
+
+
+
−
=
−+
−
+
=
+
+
=
(П1.13)
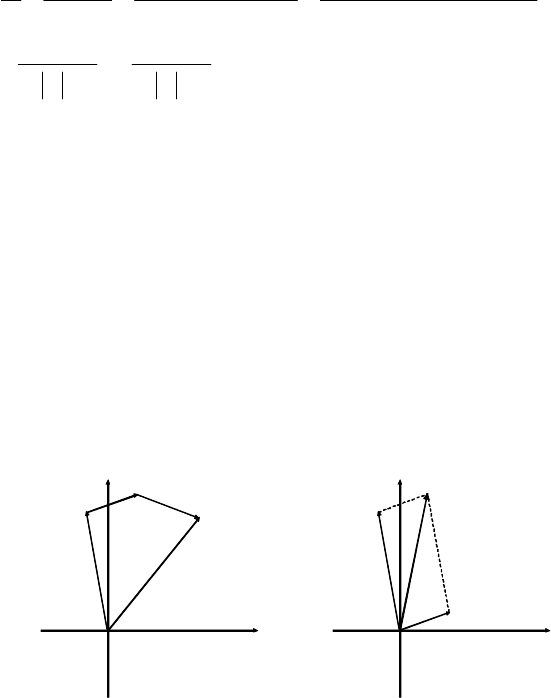
Суммирование комплексных чисел бывает удобно проводить
графически, используя правила сложения векторов. Можно выделить два
способа сложения векторов. Пусть необходимо построить вектор z, равный
сумме векторов z
1
, z
2
и z
3
. Первый способ. Построение осуществляется
следующим образом: из начала координат строят вектор z
1
, затем из конца
вектора z
1
как из начала координат строят второй вектор z
2
, из конца
вектора z
2
, как из начала координат строят вектор z
3
(Этот процесс можно
многократно повторять исходя из количества суммируемых векторов).
Вектор, выходящий из начала координат и замыкающий образованную
ломанную кривую из суммируемых векторов, является их суммой
(рис.П1.2). Второй способ основан на по парном сложении векторов.
Сначала складываются векторы z
1
и z
2
по правилу параллелограмма.
Вектор z
12
, равный сумме векторов z
1
и z
2
, есть диагональ параллелограмма
построенного на этих векторах .(рисП1.3). Искомый вектор z получают
суммированием вектор z
12
с вектором z
3
. Этот процесс так же можно
многократно повторять исходя из количества суммируемых векторов.
Вычитание векторов можно понимать как суммирование, если
предварительно направления вычитаемых векторов поменять на
противоположные.
Re
Z
1
I
m
Ů
Z
2
Z
3
Z
Re
Z
1
I
m
Ů
Z
2
Z
12
Рис. П1.2 Рис.П1.3

146
Приложение 2.
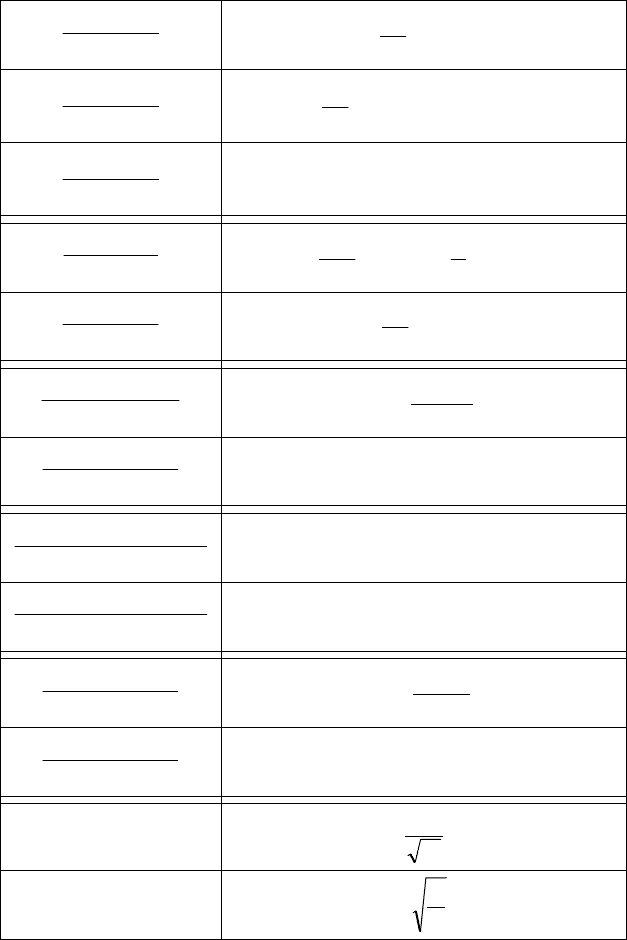
Основные оригиналы и изображения по Лапласу
)( pF )(tf
1
)(t
δ
– дельта функция
p
1
1
2
1
p
t
n
p
1
)!1( −n
t
n
, где n – целое положительное число
ap +
1
at
e
−
2
)(
1
ap +
at
te
−
3
)(
1
ap +
at
et
−2
2
1
n
ap )(
1
+
atn
et
n
−−
−
1
)!1(
1
, где n – целое
положительное число
)(
1
app +
)1(
1
at
e
a
−
−
)(
1
2
app +
)1(
1
−+
−
ate
a
at
n
app )(
1
+
]
!
)(
1[
1
0
∑
=
−
−
n
k
k
at
n
k
at
e
a
, где n – целое
положительное число
2
)( ap
p
+
at
eat
−
− )1(

147
3
)( ap
p
+
at
eatt
−
− )
2
1
1(
1
)(
+
+
n
n
ap
p
k
n
k
k
at
t
kkn
an
e
∑
=
−
−
−
0
2
)!()!(
)(!
, где n – целое
положительное число
))((
1
bpap ++
)(
1
btat
ee
ab
−−
−
−
))((
1
bpapp ++
)
11
(
11
atbt
e
a
e
babab
−−
−
−
+
))(( bpap
p
++
)(
1
atbt
aebe
ab
−−
−
−
22
1
ap +
)sin(
1
at
a
)(
1
22
app +
)]cos(1[
1
2
at
a
−
22
ap
p
+
)cos(at
22
1
ap −
)(
1
atsh
a
22
ap
p
−
)(atch
22
sincos
ap
babp
+
−
)cos( bat
+
22
cossin
ap
babp
+
+
)sin( bat
+
222
)(
1
ap +
)]cos()sin(
1
[
2
1
2
attat
a
a
−
148
222
)( ap
p
+
)sin(
2
at
a
t
222
2
)( ap
p
+
)]cos()[sin(
2
1
atatat
a
+
222
22
)( ap
ap
+
−
)cos(att
222
)(
1
ap −
)](
1
)([
2
1
2
atsh
a
atcht
a
−
222
)( ap
p
−
)(
2
atsh
a
t
2222
)(
1
bap ++
b
bt
e
at
)sin(
−
2222
)( bap
ap
++
+
)cos(bte
at−
2222
)(
sincos)(
bap
bap
++
−+
ψψ
)cos(
ψ
+
−
bte
at
2222
)(
cossin)(
bap
bap
++
++
ψψ
)sin(
ψ
+
−
bte
at
2222
)(
1
bap −+
b
btsh
e
at
)(
−
2222
)( bap
ap
−+
+
)(btche
at−
5,0−
p
t
π
1
5,1−
p
π
t
2
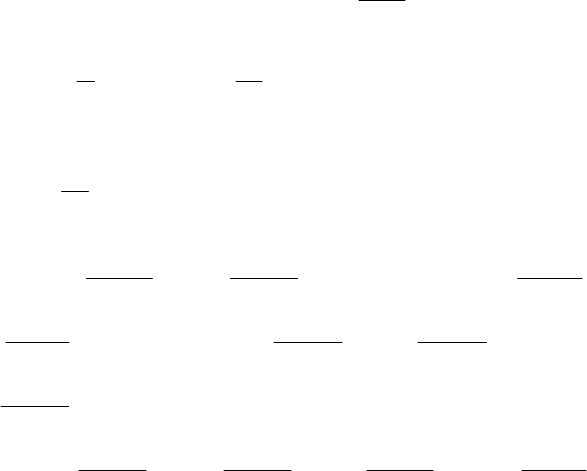
149
Ответы
Введение
1. Используя закон Ома для конденсатора (6), провести вычисления
u
C
(t), а затем по формуле (10) найти р
C
(t).
2
5,0)( ttu
C
= ,
3
5,0)( ttp
C
= при
10 ≤≤ t ;
2
)2(5,01)( −−= ttu
C
, )2)()2(5,01()(
2
tttp
C
−−−= при
31 ≤≤ t ;
2
)4(5,0)( −= ttu
C
,
3
)4(5,0)( −= ttp
C
при 43
≤
≤
t .
2. Используя закон Ома для катушки индуктивности (2), провести вы-
числения u
L
(t), а затем по формуле (9) найти р
L
(t). 1)(
=
tu
L
, ttp
L
=)( при
10 ≤≤ t ; 1)( −=tu
L
, 2)(
−
=
ttp
L
при 31
≤
≤
t ; 1)(
=
tu
L
, 4)( −= ttp
L
при
43
≤
≤ t .
3. Используя законы Ома для элементов цепи(1), (3) и (7), провести
вычисления токов во всех элементах, а затем по формулам (8), (9) и (10)
найти мгновенные мощности.
4. Воспользоваться указаниями к задаче 1.
5. Воспользоваться указаниями к задаче 2.
6. Для получения производной от ЭДС
dt
tde )(
необходимо измерять
напряжение на сопротивлении (u
R
(t)) при этом необходимо выполнение
условия
∫
〈〈 idt
C
Ri
1
или
t
i
i
RC
mx
c
Δ〈〈
. Для получения интеграла от ЭДС
∫
edt
необходимо измерять напряжение на емкости (u
C
(t)) при условии,
что
t
i
i
RC
mx
c
Δ>>
7. Воспользоваться указаниями к задаче 6.
8. а)
u
RR
R
u
21
1
1
+
=
, u
RR
R
u
21
2
2
+
=
,
21
RRR
+
=
; б) u
LL
L
u
21
1
1
+
=
,
u
LL
L
u
21
2
2
+
=
,
21
LLL += ; с) u
CC
C
u
21
2
1
+
=
, u
CC
C
u
21
1
2
+
=
,
21
21
CC
CC
C
+
=
.
9. а)
i
RR
R
i
21
2
1
+
=
, i
RR
R
i
21
1
2
+
=
,
21
21
RR
RR
R
+
=
; б) i
LL
L
i
21
2
1
+
=
,

150
i
LL
L
i
21
1
2
+
=
,
21
21
LL
LL
L
+
=
; с) u
CC
C
i
21
1
1
+
=
, u
CC
C
i
21
2
2
+
=
,
21
CCC += .
10. Воспользоваться законами Кирхгофа и последовательно выразить
токи в ветвях начиная с правого наименьшего контура.
11. Воспользоваться законами Кирхгофа и последовательно выразить
напряжения ветвей начиная с правого наименьшего контура.
12. а)
RRR ==
21
, )()(
0
tRite
=
; б) LLL
=
=
21
,
dt
tdi
Lte
)(
)(
0
=
;
с)
CCC ==
21
, dtti
C
te
∫
= )(
1
)(
0
Электрические цепи постоянного тока
1. 1) посередине сопротивления R
3
; 2) заземлить точку h.
2.
15
2
=
E В.
3.
0
2
=
E В.
4. 1)
8,22=
a
u
B; 2)
6
=
a
u
B.
5.
135
1
=
E В, 90
2
=E В, 8,1
1
=
P кВт, 550
2
−
=
P Вт.
6.
4,32
=
u В, 7=E В, 68,1
=
R Ом.
7.
47
=
R
Ом, 72
2
=E В.
8. Направление тока слева направо,
21
1
=
i A, 8
2
=
i A, 13
4
=i A,
16
5
=i
A,
8
6
=i
A.
9.
5,6
=
E В.
10.
5
1
=
i A, 8
2
=i A, 1
3
=
i A, 6
4
−
=
i A, 2
5
=
i A.
11.
424121
22421
1
)(
RRRRRR
RERRE
i
++
−+
= ,
424121
1241
2
RRRRRR
RERE
i
++
+
= ,
3
2
3
R
E
i = ,
424121
122
4
)(
RRRRRR
RRE
i
++
+
−=
.
12.
rR
E
i
+
=
1
1
,
rR
E
i
+
=
2
2
,
rR
EE
ii
+
−
==
21
63
,
rR
EE
ii
+
+
==
21
54
.
13. Удобно провести замену источника тока на два эквивалентных ис-
точника напряжения
101
RiE
=
,
402
RiE
=
внесенные соответственно в
ветви сопротивлений R
1
и R
4
.
14. 1)
20=E В, 10=R Ом; 2) 2
0
=
i A, 10
=
R Ом; 3) 10 В, 1 А.
15. 1)
)2(5
H
Ri += ; 2) iu 210
−
=
.
