Мищенко А.М. Сборник задач по линейным электрическим цепям с кратким изложением теории

61

I

00

I

01

U

1

U

2

Z

3

Z

1

Z

2

Z

4

I

02

0

него отсчитывают

потенциалы (на-

пряжения) всех

остальных. В пе-

рестроенной схе-

ме на рис. 3.9

потенциала двух

оставшихся узлов

обозначены

1

U

&

и

2

U

&

. Найдем соот-

ветственно пол-

ные проводимости этих узлов:

321

11

111

ZZZ

Y

++=

,

43

22

11

ZZ

Y +=

.

Используя первый закон Кирхгофа для двух верхних узлов, получаем си-

стему канонических уравнений

⎪

⎩

⎪

⎨

⎧

−=−+=−

−=−++=

.

1

)

11

(

,

1

)

111

(

1212221

3

2

43

0002

2121112

3

1

321

01

UYUYU

Z

U

ZZ

II

UYUYU

Z

U

ZZZ

I

&&&&&&

&&&&&

(3.25)

Решение этой системы:

;

))((

)]()([

2

243221

00024430121

1

ZZZZZZ

IIZZZIZZ

U

−+++

−++

=

&&&

&

(3.26)

.

))((

)]([

43221

2

3231210040114

2

ZZZZZZ

ZZZZZZIZIZZ

U

+++−

+++

=

&&

&

(3.27)

В силу эквивалентности преобразований эти напряжения будут

соответствовать напряжениям для двух верхних узлов отсчитанных от

нижнего узла и в исходной схеме (рис. 3.8). Поэтому, из закона Ома для

ветвей исходной схемы получаем все комплексные токи:

1

11

1

Z

UE

I

Z

&&

&

−

=

,

4

22

4

Z

EU

I

Z

&&

&

−

=

,

2

1

0

2

Z

U

I

Z

−

=

&

,

3

21

3

Z

UU

I

Z

&&

&

−

=

(3.28)

Отметим, что если определять токи, используя преобразованную схему

рис. 3.6, то необходимо помнить, относительно каких узлов проводилась

эквивалентная замена источников напряжения на источники тока, и какие

сопротивления считались при этом внутренними сопротивлениями

Рис. 3.9

62

источников. В рассматриваемом случае только токи в сопротивлениях

2

Z

и

3

Z

во всех схемах будут одинаковыми.

В связи с этим бывает более удобно проводить расчеты без

эквивалентных преобразований, используя непосредственно закон Ома и

первый закон Кирхгофа. Поэтому повторим расчеты данным способом,

используя непосредственно схему на рис. 3.8. Оставляя обозначение

потенциалов прежним, получаем систему уравнений

⎪

⎩

⎪

⎨

⎧

=−

−

+

−

=

−

+

−

+

−

.0

,0

0

00

4

22

2

21

3

12

2

1

11

I

Z

UE

Z

UU

Z

UU

Z

U

Z

UE

&

&&&&

&&&&&

. (3.29)

Первое уравнение записано для верхнего левого узла, второе – для

верхнего правого узла. Для упрощения написания уравнений все токи

считались втекающими, так как знаки токов автоматически определяются

законом Ома. Во втором слагаемом первого уравнения для наглядности

явно записано нулевое значение потенциала нижнего узла. Проведя

математические преобразования, легко убедиться, что данная система

сводится к системе (3.25) если учесть выражения для токов

01

I

&

и

02

I

&

,

полученных ранее по правилам эквивалентных преобразований

источников напряжения в источники тока.

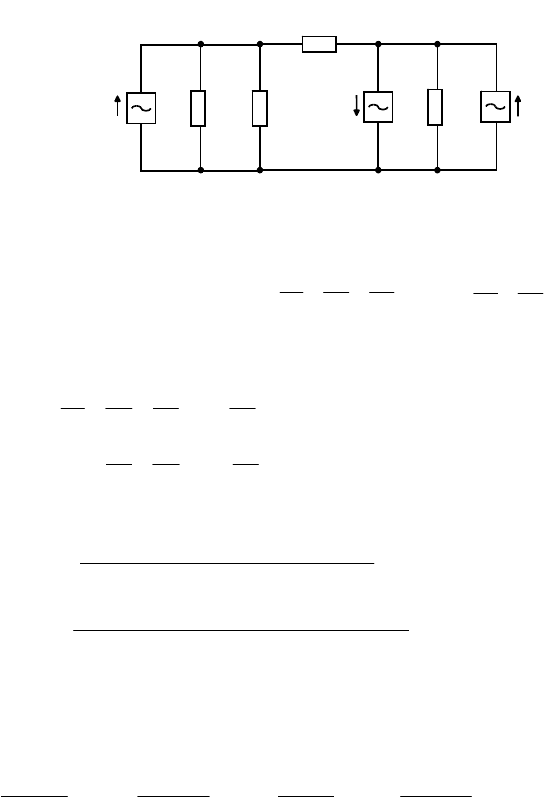
Пример 4. Расчет методом узловых напряжений схем с ветвями,

состоящими из источников ЭДС. Параметры схемы на рис. 3.10:

jЕ =

1

&

В,

1

2

=Е

&

В,

jЕ −=

3

&

В,

jZ

−

=

1

Ом,

1

2

=

Z

Ом,

1

3

=

Z

Ом,

1

4

=Z

Ом,

jZ =

5

Ом.

В этой схеме две ветви состоят

только из источников ЭДС (

1

Е

&

и

3

Е

&

).

За базисный узел возьмем крайний

правый узел. Потенциал этого узла

равен нулю:

0

=U

&

. Тогда потенциал

внутреннего узла, где сходятся

сопротивления Z

1

, Z

2

и Z

4

опре-

деляется идеальным источником на-

пряжения

3

Е

&

:

jEU −==

32

&&

В. Если положить потенциал нижнего узла

равным

3

U

&

, то потенциал верхнего узла jUEUU +=+=

3131

&&&&

. Таким

Z

4

Z

3

E

1

Z

5

Z

2

Z

1

E

2

E

3

Рис. 3.10

63

образом, хотя общее число неизвестных равно двум, достаточно найти

либо

1

U

&

, либо

3

U

&

.

Проведем решение с использованием дополнительной неизвестной

01

I

&

,

соответствующей току в ветви с

1

Е

&

. Будем считать, что его направление

совпадает с направлением ЭДС. Таким образом, общее количество

неизвестных стало равным трем. Составим систему уравнений по первому

закону Кирхгофа для верхнего и нижнего узла. При этом потенциал

внутреннего узла будем сразу считать известным (

32

EU

&&

= ). Выражая

токи в ветвях через закон Ома и полагая, для упрощения, что все они

втекают в узлы, получаем

⎪

⎩

⎪

⎨

⎧

=−

−

+

−

=+

−

+

−

.0

0

,0

0

01

5

3

4

33

01

3

1

13

I

Z

U

Z

UE

I

Z

U

Z

UE

&

&&&

&

&&

(3.30)

Преобразуем эту систему к каноническому виду:

⎪

⎩

⎪

⎨

⎧

−=−+

=−+

.)(

,)(

0134354

0131131

IEYUYY

&&&

. (3.31)

Видно, что система (3.28) могла быть записана, если бы при ее записи

“мысленно” считать ЭДС

1

Е

&

источником тока

01

I

&

. Такие “мысленные”

замены лишних источников ЭДС на источники тока значительно ускоряют

запись уравнений Кирхгофа. Полная система уравнений для определения

узловых напряжений получается объединением системы (3.31) с

уравнениями, связывающими узловые напряжения и ЭДС источников

⎪

⎩

⎪

⎨

⎧

=−

=++

=−+

.

,)(

231

3401354

3101131

EUU

EYIUYY

&&&

. (3.32)

Система (3.32) приведена к виду удобному для решения матричным

способом. Система состоит из трех независимых уравнений и может быть

решена в общем виде относительно трех неизвестных

1

U

&

,

3

U

&

и

01

I

&

.

Решение системы (3.32) сильно упрощается, если воспользоваться тем,

что токи

01

I

&

входят в уравнения с разными знаками. Поэтому,

64

суммирование первых двух уравнений, устраняет

01

I

&

и понижает ранг

системы на единицу. Эту особенностью написания систем уравнений

Кирхгофа эффективно использовать сразу, следуя выше сформу-

лированному правилу. В данном случае оно гласит, что сумма токов

втекающих в ЭДС

1

Е

&

равна сумме токов из неё вытекающих:

3154

IIII

&&&&

+=+

. (3.33)

Тогда имеем одно уравнение

1331115334

)()( UYEUYUYUEY

&&&&&&

+−=−−

, (3.34)

которое является суммой двух первых уравнений в системе (3.32).

Используя численные значения и уравнение

231

EUU

&&&

=− , получаем

jU −=1

3

&

и

1

=U

&

. Зная все потенциалы, по закону Ома находятся все

токи в ветвях. Например, ток в Z

3

:

π

4

5

3

21

1

0

j

ej

j

Z

U

I =−−=

−

=

−

=

&

. (3.35)

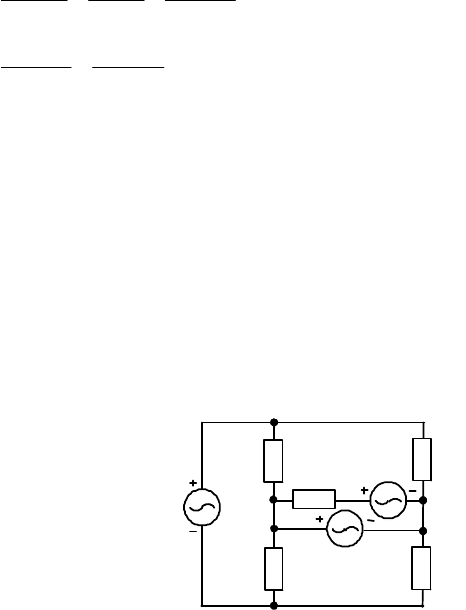
Пример 5. Расчет методом суперпозиции. Найдем токи в ветви с

сопротивлением Z

3

для схемы на рис. 3.8. Ток в Z

3

будем искать как сумму

токов созданных каждым источником:

IEEZ

IIII

&&&&

++=

213

. (3.36)

Тока

1

E

I

&

от идеального источника

1

Е

&

рассчитаем по схеме на

рис. 3.11. Она получена согласно правилам исключения источников

энергии. Источник тока

00

I

&

отсоединили, и данная ветвь стала

разомкнутой, а исключение источника ЭДС

2

Е

&

провели путем заменой

его проводом с нулевым сопротивлением. Для краткости обычно говорят,

E

1

I

E

1

Z

1

Z

2

Z

3

Z

4

Рис. 3.11 Рис. 3.12

E

2

Z

3

E

Z

1

E

Z

2

Z

4

I

E

2

65

что источники тока “размыкаются”, а источники ЭДС “замыкаются” или

накоротко шунтируются.

Эффективное сопротивление, присоединенное к источнику E

1,

равно

432

243

11

)(

ZZZ

ZZ

ef

++

+

+=

. (3.37)

Ток через сопротивление Z

1

равен

1

ef

Z

E

I

&

=

. (3.38)

Тогда

43

111

43

1

ZZ

IZE

ZZ

U

I

E

+

−

=

+

=

&&&

&

. (3.39)

Следующий этап – расчет тока

,

2

E

I

&

вызванного источником

2

E

&

. Он

проводится по схеме, получаемой “размыканием” источника тока и

“замыканием” источника

1

E

&

(рис. 3.12). Эффективное сопротивление, при-

соединенное к источнику

2

E

&

,

равно

21

432

ZZ

ZZZ

ef

+

++=

. (3.40)

Поэтому ток

2

E

I

&

с учетом полярности равен

2

ef

E

Z

E

I

&

−=

. (3.41)

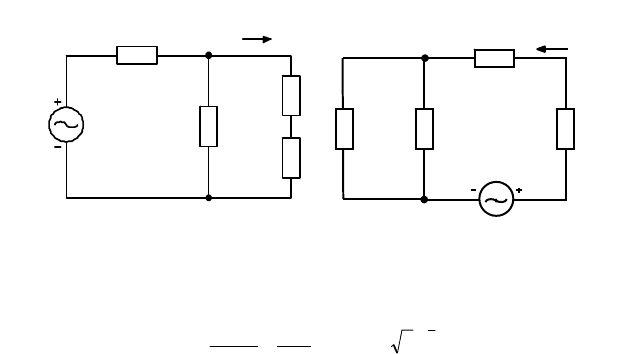
Последний ток

I

&

рассчиты-

вается по схеме, приведенной на

рис. 3.13. Она получена “замы-

канием” источников

1

E

&

и

2

E

&

.

Найдем сначала напряжение на

источнике тока. Оно равно

3efI

ZIU

&&

= , где эффективное

сопротивление Z

ef3

, подсоеди-

ненное к идеальному источнику

тока. Величину этого сопротивления найдем по формуле

I

Z

2

I

00

Z

1

Z

3

Z

4

Рис. 3.13

66

4343

111

efef

ZZZZ +

+=

, (3.42)

в которой

)(

21214

ZZZZZ

ef

+

= . Рассчитав U

&

, найдем искомый ток:

43 ef

I

ZZ

U

I

+

=

&

. (3.43)

Наконец, подставив все найденные значения токов в уравнение (3.36),

получим искомый ток через сопротивление Z

3

.

Преимущество данного метода в возможности анализа вкладов каждого

источника в окончательный результат.

Пример 6. Расчет тока в ветви из пассивных элементов методом

эквивалентного генератора. Найдем ток в сопротивлении Z

3

в схеме

рис. 3.8. Заменим всю цепь, к которой

присоединено сопротивление Z

3

эквива-

лентным генератором напряжения

(рис. 3.14). Найдем ЭДС генератора

xx

U

&

и его внутреннее сопротивление Z

0

.

Величину Z

0

рассчитаем по схеме,

приведенной на рис. 3.15. Она получена

из исходной схемы путем удаления сопротивления Z

3

и выключения ис-

точников: источник тока отсоединяется, источник напряжения “замы-

кается”. Величина Z

0

равна сопротивлению цепи между точками 1 и 2

21

40

ZZ

+

+=

. (3.44)

ЭДС генератора равна напряжению холостого хода, рассчитываемого

Z

0

Z

3

U

х

2

1

Рис. 3.14

Z

2

Z

1

Z

4

1

2

Z

1

Z

2

E

1

I

00

U

1

U

2

1 2

Z

4

E

2

U=0

Рис. 3.15 Рис. 3.16

67

как разница потенциалов

1

U

&

и

2

U

&

в точках 1 и 2 схемы рис. 3.16:

21

UUU

xx

&&&

−=

. Значения

1

U

&

и

2

U

&

вычисляются по формулам

,

21

1

21

ZZ

E

ZU

+

=

&

(3.45, а)

.

00422

IZEU

&&&

−=

(3.45, б)

Тогда согласно схеме рис. 3. 14 ток в сопротивлении Z

3

.

))((

)()(

2103

0021422112

03

3

ZZZZ

IZZZEZZEZ

ZZ

U

I

xx

z

++

+++−

=

+

=

&&&&

&

(3.46)

Преимущество данного метода в быстроте получения результата.

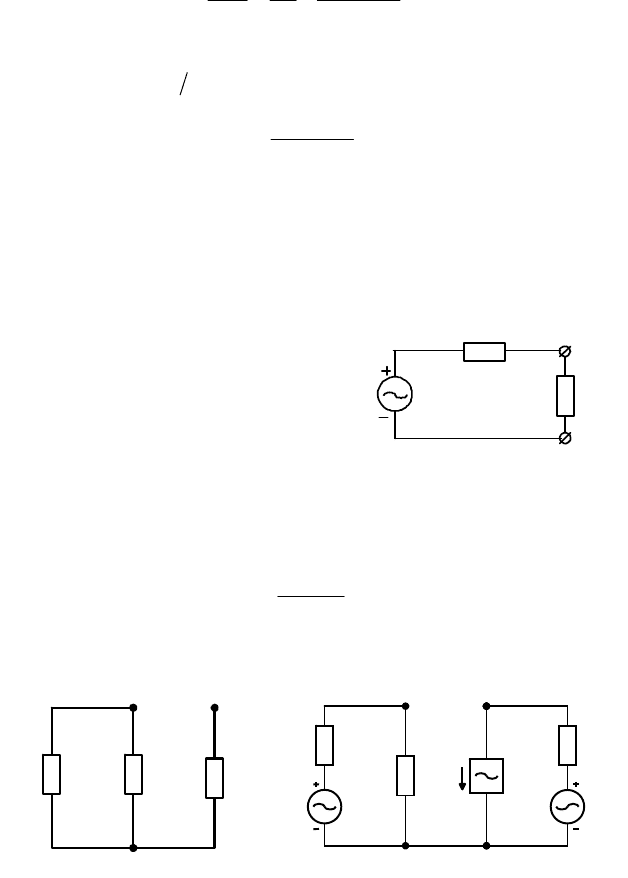
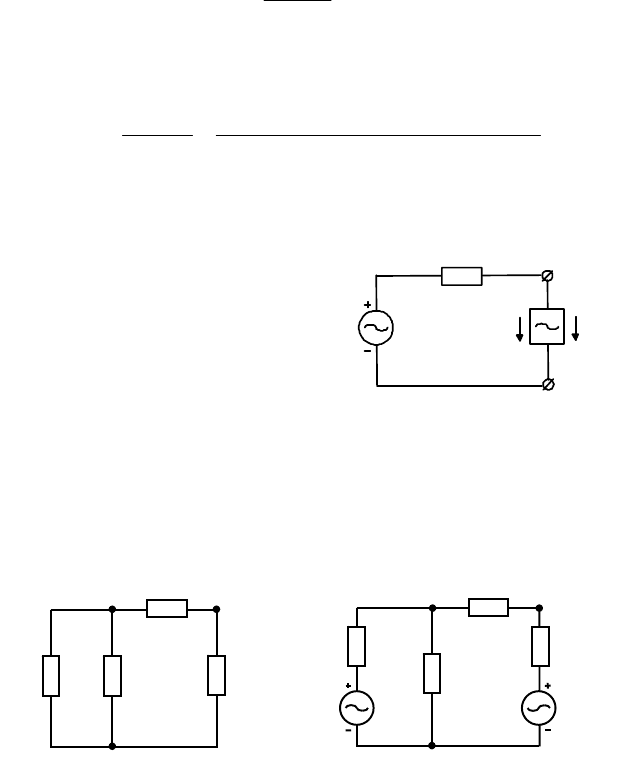
Пример 6. Расчет падения напряжения на ветви с идеальным

источником тока методом эквивалентного генератора. Найдем падение

напряжения на ветви образованной

идеальным источником тока

00

I

&

в

схеме рис. 3.8. Заменим всю цепь, к

которой присоединен источник тока

00

I

&

, эквивалентным генератором

напряжения (рис. 3.17). Найдем ЭДС

генератора

xx

U

&

и его внутреннее

сопротивление Z

0

.

Величину Z

0

рассчитаем по схеме, приведенной на рис. 3.18. Она

получена из исходной схемы рис. 3.8 путем удаления источника тока

00

I

&

и

“замыкания” ЭДС всех источников напряжения. Величина Z

0

соответствует сопротивлению цепи между точками 1 и 2.

Z

0

I

00

2

1

U

хх

U

21

Рис. 3.17

Z

2

Z

1

Z

4

1

2

Z

3

Z

4

E

2

Z

3

Z

1

Z

2

E

1

U

1

=0

U

2

1

2

U

Рис. 3.18 Рис. 3.19

68

212143

421213

2143

4213

0

))((

)(

ZZZZZZ

ZZZZ

Z

+++

++

=

++

+

=

. (3.44)

ЭДС генератора, равная напряжению холостого хода, рассчитывается

как разница потенциалов

1

U

&

и

2

U

&

в точках 1 и 2 на схеме рис. 3.19:

12

UUU

xx

&&&

−=

. Потенциал

1

U

&

возьмем равным нулю, Для определения

2

U

&

необходимо сначала найти ток в ветви источника ЭДС

2

Е

&

. Этот ток

можно найти либо методом контурных токов, либо с помощью метода

узловых потенциалов. Применим метод узловых потенциалов. Найдем

сначала потенциал

U

&

, указанный на рис. 3.19. С этой целью запишем

уравнение Кирхгофа для токов в узле

U

&

0

43

2

21

1

=

+

−

+

−

+

−

ZZ

UE

Z

U

Z

UE

&&&&&

. (3.47)

Решение уравнения (3.47)

214321

212431

))((

ZZZZZZ

ZZEZZE

U

+++

++

=

&&

&

. (3.48)

Теперь найдем ток в сопротивлении Z

3

214321

12221

43

2

))((

)(

ZZZZZZ

ZEZEE

ZZ

EU

I

+++

−−

=

+

−

=

&&&&&

&

(3.49)

и, наконец, получим напряжение холостого хода

214321

323212421

32

))((

ZZZZZZ

ZZZZZEZZE

IZUUU

xx

+++

−−+

=+==

&&

&&&&

. (3.50)

Используя найденные выражения для

xx

U

&

и Z

0

, а так же учитывая

направление тока в источнике, получим в соответствие со схемой рис. 3.17

напряжения

21

U

&

на источнике тока:

00021

IZUU

хх

&&&

+= . (3.51)

В силу громоздкости общего выражения для

21

U

&

опустим подстановку

xx

U

&

и Z

0

в равенство (3.51).

Преимущество данного метода в наглядности получения результата.

69

Задачи

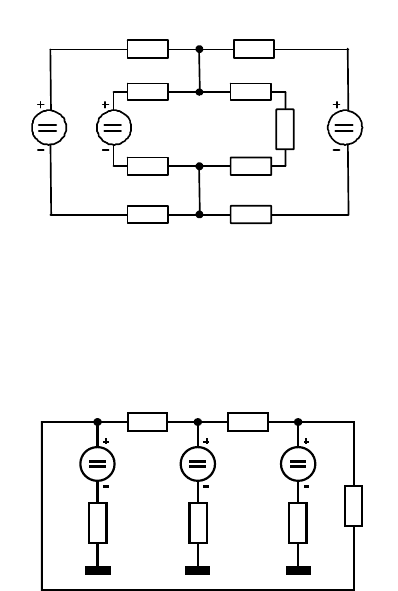
1. Методом контурных токов найти токи во всех ветвях схемы.

2.

Методом контурных токов найти токи во всех ветвях. Параметры

схемы: R

1

= R

2

= 15 Oм, R

3

= 5,5 Oм R

4

= 20 Oм, E

1

= E

2

= 100 B.

3.

Методом контурных токов найти токи в ветвях схемы приведен-

ной в задаче 13 § 1.

4.

Каким

методом проще

найти все токи

в ветвях: мето-

дом контурных

токов, методом

узловых потен-

циалов или ме-

тодом суперпо-

зиции. Рассмо-

трите два слу-

чая: 1) сопротивления всех резисторов различны; 2) все сопротивления

равны R.

E

1

R

2

R

5

E

3

E

2

E

4

R

1

R

4

R

3

R

6

E

1

E

2

R

1

R

2

R

3

R

4

Рис. к задаче 1 Рис. к задаче 2

E

R

5

I

0

R

3

R

1

R

2

R

4

E

R

3

R

5

R

1

R

2

R

4

Рис. к задаче 4 Рис. к задаче 5

R

31

R

23

R

12

U

1

U

2

U

3

I

1

I

3

I

2

R

2

U

2

U

1

R

1

R

3

I

2

I

1

I

3

U

3

O

Рис. к задаче 6

70

5.

Методом контурных токов или методом узловых потенциалов

проще рассчитать схему? Проведите этот расчет.

6.

Выразить сопротивления резисторов R

12

, R

23

, R

31

треугольника

через сопротивления резисторов

R

1

, R

2

, R

3

звезды и наоборот, так чтобы

данные цепи были эквивалентны, относительно внешних участков схемы

(токи, втекающие в цепи, и потенциалы на внешних узлах остаются неиз-

менными). Всегда ли

такие преобразования

возможны, если, напри-

мер, вместо резисторов

взять емкости или ин-

дуктивности?

7.

Методом узловых

потенциалов найти токи

во всех ветвях схе-

мы.

E

1

= 13 B, E

2

= E

3

=

= 12 B,

R

1

= R

3

= R

5

=

R

8

= 0,05 Oм, R

2

= R

9

=

= 0,125 Oм,

R

4

= R

6

=

= 0,1 Oм,

R

7

= 4,8 Ом.

8.

Найти токи во всех ветвях схемы сначала методом узловых потен-

циалов, а затем воспользоваться эквивалентам преобразованием треуголь-

ника в звезду и решить

задачу методом контурных

токов. (Какое решение

проще?) Параметры схе-

мы:

E

1

= E

3

= 4 B,

E

2

= 1 В, R

1

= 10 Oм,

R

2

= 50 Oм, R

3

= 5 Oм,

R

4

= 30 Oм, R

5

= 14 Oм,

R

6

= 20 Oм.

9.

Методом суперпо-

зиции решить задачу 12 § 1.

10. Пользуясь теоремой

об эквивалентном источнике найти ток в ветви сопротивления R

5

схемы

задачи 5.

11. Пользуясь теоремой об эквивалентном источнике найти ток в

ветви источника

E

2

схемы задачи 7.

12.

Пользуясь теоремой об эквивалентном источнике найти ток в

ветви сопротивления R

5

схемы задачи 13 §1.

E

1

R

1

R

1

R

3

R

4

R

2

R

5

R

6

R

1

R

8

R

9

E

2

E

3

R

7

Рис. к задаче 7

R

3

R

4

R

2

R

1

R

6

R

5

E

3

E

2

E

1

Рис. к задаче 8

Мищенко А.М. Сборник задач по линейным электрическим цепям с кратким изложением теории

Подождите немного. Документ загружается.