Мищенко А.М. Сборник задач по линейным электрическим цепям с кратким изложением теории

Подождите немного. Документ загружается.

проводимость ветви, соединяющей узел s с узлом k;

при i = k и

1−=

при i ≠ k. В матричном виде система уравнений (3.8) имеет вид

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−−

−

1,12,11,1

1,22221

1,11211

1,0

...

...........................................

...........

...

qqqq

YYY

. (3.9)

Отметим, что

ikki

YY = и получаемая система симметрична

относительно главной диагонали. Если узлы не связаны между собой, то в

этом месте в матрице проводимостей ставиться ноль.

Общее решение системы (3.9) можно получить методом Крамера

∑

−

ikik

, (3.10)

где Δ – определитель системы, Δ

– алгебраическое дополнение к

элементу

Проиллюстрируем получение систем уравнений (3.7), (3.8) на ситуации

некоторого k-го узла для участка цепи, изображенного на рис. 3.2а.

Использование первого способа приводит к уравнению Кирхгофа

)(

−+

−

kkk

UEU

&&&&&&&

. (3.11)

k+2

k+1

0k-1

k+4

k+2

k+3

k+2

k+1

0k-1

k+4

k+2

k+3

Рис. 3.2

При записи уравнения (3.11) использовалось, что ток в ветви либо задан

источником тока, либо определен по закону Ома. При этом направление

токов в ветвях с пассивными элементами было выбрано в сторону узла k.

Справедливость такого выбора основано на том, что закон Ома

автоматически устанавливает связь направления тока с разностью

потенциалов на

пассивном элементе. Уравнение (3.11) легко преобразуется

к каноническому виду

111

)

111

(

−

−−−++=+

kkk

ZZZ

&&&&&

. (3.12)

По второму способу уравнение (3.12) получается механически при

использовании следующего порядка действий. Вначале заменяется

источник напряжения, образованный сопротивлением ветви

источником ЭДС

, на эквивалентный источник тока c

kk0

внутренним сопротивлением

(рис. 3.2, б). Затем вычисляется полная

проводимость узла, равная сумме проводимостей всех ветвей узла k, и,

наконец, записывается уравнение.

Метод узловых напряжений при аналитических расчетах имеет

преимущество перед методом контурных токов, тогда когда ранг системы

(3.7) или (3.8) меньше ранга системы (3.1), т. е. когда справедливо

неравенство q - 1 < p - q + 1 или 2(q -

1) < p.

При записи систем (3.7) или (3.8) полагалось, что все источники

напряжения можно преобразовать в источники тока, т. е. они либо имеют

внутреннее сопротивление, либо если они идеальны, то последовательно с

ними стоят пассивные элементы, которые определяют их внутренние

сопротивления. В случае, когда ветви цепи образуют идеальные источники

напряжения – источники ЭДС,

расчет цепи методом узловых потенциалов

требует специального подхода.

• В схемах, содержащих одну такую ветвь, за базисный узел берут

один из узлов этой ветви. Тогда напряжение другого узла равно ЭДС

источника. Это позволяет отказаться от одного уравнения с участием этого

узла, уменьшив тем самым ранг общей системы на единицу.

• В

схемах с несколькими ветвями, состоящими только из источников

ЭДС, вводят новые неизвестные:

– токи в этих источниках. Токи

не могут быть бесконечными, так как они задаются суммой токов в ветвях,

присоединенных к одному из узлов источника. Такой подход позволяет

формально записывать систему уравнений Кирхгофа для токов в узлах,

“мысленно” считая источники ЭДС идеальными источниками тока с

неизвестными токами

. Добавляя к этой системе уравнения

(

ikk

EUU

&&&

±=

) для потенциалов узлов, соединенных источниками ЭДС,

получают полную систему независимых уравнений. Такую систему можно

сильно упростить, если воспользоваться тем обстоятельством, что

введенные токи

в уравнения Кирхгофа для узлов соединенных

источником ЭДС, входят с разными знаками. Действительно,

в один

узел втекает, а из другого вытекает. Поэтому сложением этих уравнений

введенные токи устраняются, что приводит к понижению ранга системы

уравнений Кирхгофа на количество ветвей, состоящих из идеальных

источников напряжения. Таким образом, введенные токи

, служат лишь

для упрощения процедуры получения системы уравнений Кирхгофа. При

наличии навыка, данная система уравнений может быть непосредственно

получена, если при ее написании придерживаться правила: для двух узлов

связанных источником ЭДС записывать сразу одно уравнение из условия,

что сумма токов, втекающих в эту ветвь, равна сумме токов из нее

вытекающих.

Последний способ применим и к случаю, когда ветвь имеет нулевое

сопротивление (например, амперметр), так как в этом случае на концах ее

будут одинаковые потенциалы.

Метод суперпозиции (наложения)

Метода суперпозиции основан на использовании независимости от

протекающего тока пассивных элементов и внутренних сопротивлений

активных элементов. Поэтому уравнения Кирхгофа, как в интегро-

дифференциальном, так

и в комплексном виде являются линейными. Это

позволяет рассматривать воздействия источников энергии на

электрическую цепь независимо друг от друга. Метод реализуют как для

токов, так и для узловых потенциалов. В первом случае токи в ветвях или

контурах рассчитывают как алгебраическую сумму токов, возникающих

либо от каждого источника в отдельности, либо

от групп источников, на

которые они предварительно разбиваются. Во втором случае узловые

напряжения любого узла находят алгебраическим сложением узловых

напряжений, созданных на этом узле либо каждым источником, либо

произвольной группой источников. Разбиение источников на группы

определяется удобством расчета и для каждой цепи производиться

индивидуально.

Реализацию метода осуществляют последовательным расчетом токов

или

узловых напряжений с одним источником или с целой группой

источников, имеющихся в цепи. С этой целью все другие источники

энергии отключаются. Для этого в них выключают сторонние

электродвижущие силы (генераторы). Поэтому в цепи вместо источников

остаются лишь их внутренние сопротивления. Это приводит к тому, что

ветви с идеальными источниками тока разрываются, а места

присоединения источников ЭДС соединяются (говорят, что источники

ЭДС шунтируются накоротко). Окончательный расчет завершают

алгебраическим сложением полученных решений.

Метод эквивалентного источника

Этот метод основан на теореме об эквивалентном источнике

(активном двухполюснике).

Теорема

Тевенена и Нортона. Любая сколь угодно сложная линейная

схема, которая может соединяться с другими схемами только посредством

двух узлов, эквивалентна генератору с задающим напряжением, равным

напряжению холостого хода и внутренним сопротивлением, равным

входному сопротивлению схемы, или генератору с задающим током,

равным току короткого замыкания, и внутренней проводимостью, равной

входной проводимости схемы

Теорема об эквивалентном источнике напряжения (теорема Тевенена).

Рассмотрим сначала вариант с источником напряжения. Утверждается, что

ток в любой ветви mn линейной электрической цепи не изменится, если

электрическую схему, к которой подключена данная ветвь, заменить

эквивалентным источником напряжения. Такой источник напряжения

имеет источник ЭДС (генератор) с

ЭДС, равной напряжению на

узлах m,

n при разомкнутой ветви mn, т. е

равной напряжению холостого хода –

. При этом его внутреннее со-

противление равно входному сопро-

тивлению Z

схемы со стороны узлов

m, n, при отключенных в ней

источниках энергии. Величина Z

определяется при отключенных в

схеме источниках энергии. На

рис. 3.3, а эта схема изображена пря-

моугольником, в котором

iii

ZIE ,,

обозначены имеющиеся в цепи активные и пассивные элементы, а на

рис. 3.3, б она заменена эквивалентным источником напряжения. Таким

образом, в простом случае, когда ветвь mn состоит только из пассивных

элементов, имеющих полное сопротивление

, расчет тока в ветви mn

можно проводить с помощью простой формулы:

, I

а)

б)

Рис. 3.3, а, б

, (3.13)

Справедливость теоремы вытекает из принципа суперпозиции,

согласно которому ток в ветви mn можно рассчитывать как сумму токов в

цепях, представляющих последовательную замену исходной цепи

схемами, изображенными на рис. 3.4. Квадратом изображена схема, к

которой подсоединена ветвь mn. Буква А в квадрате обозначает, что в

такой схеме имеются как активные (внутренние источники

напряжения и

тока), так и пассивные элементы, а буква П показывает, что схема состоит

только из пассивных элементов, которые остались после отключения

имевшихся источников энергии. Выключение источников осуществляется

путем отключения их электродвижущих сил, т. е. вместо источников в

схеме оставляют их внутренние сопротивления.

Включим последовательно в ветвь mn навстречу друг другу

два

одинаковых источника ЭДС

(правая верхняя схема). Это включение

согласно принципу суперпозиции не изменит ток в ветви mn. Далее, для

расчета тока в ветви mn применим еще раз метод суперпозиции, для этого

i = 0

Рис. 3.4

полученную схему разобьем на две схемы (центральная часть рисунка).

Первая (левая) схема отличается от исходной цепи только наличием в

ветви mn одной ЭДС

, так как в ней оставлены включенными все

имевшиеся источники энергии. Во второй (правой) же схеме включенной

оставлена только вторая ЭДС

. Исходный ток ветви mn будет равен

сумме токов, которые текут в ветвях mn в этих двух схемах. Выберем

теперь величину

такой, чтобы в ветви mn левой схеме ток стал равен

нулю. Для этого величину

возьмем равной напряжению холостого

хода (

) на зажимах mn и направим её против

, т. е.

mnmn

−=

Тогда во правой схеме:

mnmn

. Такой выбор

приводит к тому, что

первая схема эквивалентна разрыву, а ток во второй схеме становиться в

точности равным току ветви mn в исходной схеме. Наглядно это отражено

с помощью схем приведенных в нижней части рис. 3.4. Таким образом,

нижнюю правую схему можно рассматривать как эквивалентный источник

напряжения с нагрузкой в виде ветви

mn. Причем такой источник

напряжения имеет ЭДС равную

и внутреннее сопротивление равное

сопротивлению рассматриваемой схемы со стороны ветви mn, в которой

отключены все ее внутренние источники. Теорема доказана.

Таким образом, ток в ветви mn действительно может рассчитываться по

простой схеме приведенной на рис. 3.3, б.

Отметим, что ветви mn не обязательно должна состоять только из

пассивных элементов. При доказательстве

теоремы Теветена физическая

природа ветви mn не существенна. Например, при наличии в ветви

источника ЭДС

ток вычисляется по формуле

. (3.14)

Знак “+” в формуле (3.14) берется при

совпадений направлений

, а

знак “–”, когда они противоположны.

При наличии в выделенной ветви

идеального источника тока, так же

можно применять теорему Тевенена, но

в этом случае она позволяет найти

падение напряжения на данной ветви.

На рис. 3.5 приведена такая схема,

которая получена после замены остальной электрической цепи экви-

Рис. 3.5

валентным источником напряжения. Напряжение на такой ветви опре-

деляется формулой

IZUU

&&&

±=

. (3.15)

Знак “+” в формуле (3.15) берется при противоположных направлениях

, а знак “–”, когда направления совпадают.

Расчеты данным методом можно проводить одновременно для двух и

нескольких ветвей сложной активной схемы.

Теорема об эквивалентном источнике тока (теорема Нортона). Эта

теорема утверждает, что ток в любой ветви mn линейной электрической

цепи не изменяется, если электрическую цепь, к которой подключена

ветвь, заменить эквивалентным источником

тока; ток этого источника

должен быть равен току, проходящему между узлами m и n, замкнутыми

накоротко (

), а внутренняя проводимость источника (

) должна

равняться входной проводимости

пассивной электрической цепи со

стороны узлов m и n при разомкнутой

ветви mn. Таким образом, расчет тока в

ветви mn можно проводить с помощью

простой схемы приведенной на рис. 3.6,

в которой идеальный источник тока

имеет ток равный

Справедливость теоремы Нортона основывается на эквивалентном

преобразовании источника напряжения в источник тока. В соответствии с

теоремой об эквивалентном источнике напряжения (теоремой Тевенена)

приведем, как это было сделано выше, исходную схему к простой схеме,

изображенной на рис. 3.3. Данный источник напряжения преобразуем в

эквивалентный источник тока с внутренней проводимости

1 ZY

, (3.16)

где значения

и Z

те же, что и в источнике напряжения.

Тогда ток через ветвь mn рассчитывается как

mnmn

ZZZ

IZZ

)(

&&&

, (3.17)

где

mnmn

ZY 1=

Расчеты данным методом можно обобщить и на случаи наличия в ветви

mn, как идеальных источников напряжения, так и идеальных источников

0mn

Рис. 3.6

тока, а так же использовать его для одновременного расчета для двух и

нескольких ветвей.

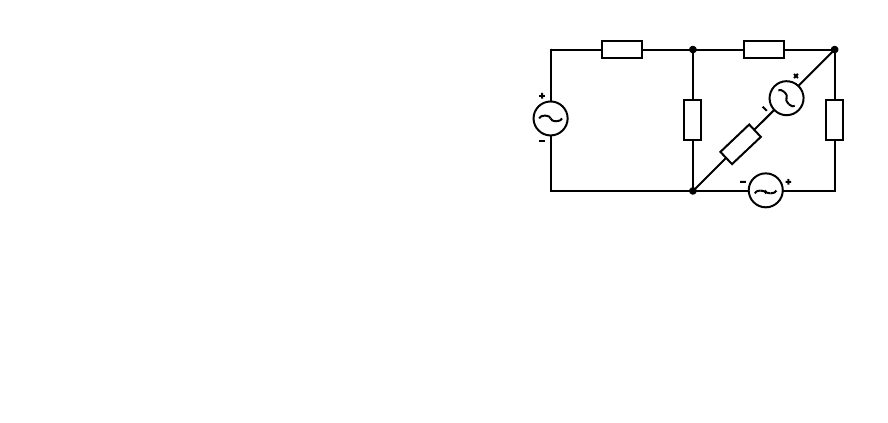
Пример 1. Расчет методом контурных токов. Расчеты проведем для

цепи рис. 3.7. Неза-

висимые контуры для

системы уравнений

Кирхгофа выберем

двумя способами: 1) с

использованием дерева

схемы; 2) последова-

тельным исключением

ветвей.

Дерево схемы обра-

зуется ветвями содер-

жащими

сопротивле-

ния Z

и Z

. Оно

включает все узлы и поочередное присоединение к этим ветвям других

ветвей образует всю схему. Присоединение ветви с сопротивлением Z

образует первый контур, подсоединение ветви с сопротивлением Z

–

второй контур, а присоединение ветви с сопротивлением Z

– третий

контур. Возникающая система контуров состоит из неперекрывающихся

независимых контуров. Все контурные токи положим текущими по

часовой стрелке. Тогда каноническая система уравнений имеет вид

⎪

⎩

⎪

⎨

⎧

++−=−

−+++−=−

+−+=

,)(0

,)(

,0)(

35424132

342432122

3221211

IZZIZIEE

IZIZZZIZE

IIZIZZE

&&&&&

&&&&

(3.18)

а ее матричный – вид

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+−

−++−

−+

⎟

⎠

⎞

⎜

⎝

⎛

−

544

44322

221

)(0

)(

0)(

ZZZ

ZZZZZ

ZZZ

(3.19)

Видно, что матрица сопротивлений имеет симметрию относительно

главной диагонали и что сопротивления, принадлежащие двум контурам,

входят со знаком минус.

Найдем теперь независимые контуры последовательным исключением

ветвей. Этим способом можно выбрать, как неперекрывающиеся контуры,

так и перекрывающиеся. Например, если в качестве исходного контура

Рис. 3.7

Рис.

3.1.2

взять контур, состоящий из ветвей с сопротивлениями Z

, Z

и Z

, то после

размыкания ветви с сопротивлением Z

, можно выбрать, либо правый

контур, либо левый. Дальнейшее размыкание любой ветви устраняет

замкнутые контуры. Найденная система контуров взаимно не

перекрывается и совпадает с ранее полученной. Возьмем теперь в качестве

исходного контура самый большой контур, огибающий всю схему.

Разомкнем ветвь с

и возьмем в качестве второго контура замкнутый

контур из ветвей, содержащих сопротивления Z

, Z

и Z

. Отсоединим

ветвь с сопротивлением Z

, оставшийся последний контур будет третьим.

Полученная система контуров содержит перекрывающиеся контуры.

Пусть все токи имеют направление по часовой стрелке. Тогда

каноническая система уравнения Кирхгофа имеет вид

⎪

⎩

⎪

⎨

⎧

+++−=−

+++=

−+++=−

35421532

3221111

3521153121

)(0

,0)(

,)(

IZZIIZEE

IIZZIZE

IZIZIZZZEE

&&&&&

&&&&

&&&&&

(3.20)

или в матричном виде

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+−

−++

⎟

⎠

⎞

⎜

⎝

⎛

−

545

211

51531

)(0

0)(

)(

ZZZ

ZZZZZ

. (3.21)

Видно, что матрица сопротивлений имеет симметрию относительно

главной диагонали. Однако знаки общих сопротивлений зависят от того,

являются контуры перекрывающимися или нет. При не перекрывающихся

контурах знак минус, а при перекрывающихся контурах знак плюс.

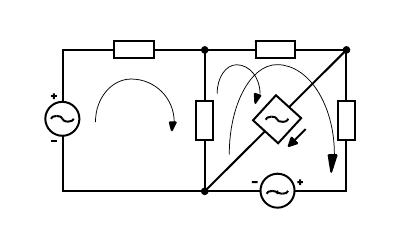
Пример 2. Расчет

методом контурных

токов при наличии

ветвей с идеальными

источниками тока.

Схема на рис. 3.8 как

схема в первом

примере имеет пять

ветвей и три узла.

Поэтому у неё три

независимых контура

(

3)1( =−− qp ).

Рис. 3.8

Однако, наличие в схеме идеального источника тока упрощает расчет, так

как достаточно найти только два неизвестных контурных тока, а в контуре,

содержащем источник тока, приравнять его току источника. Выберем

контур включающий источник тока. Пусть он будет состоять из ветвей

образованных сопротивлениями Z

, Z

и идеальным источником тока

Контурный ток в этом контуре будет равен току идеального источника

001

. Разомкнем ветвь, содержащую идеальный источник тока. В

качестве второго контура выберем контур, состоящий из сопротивлений Z

и Z

и источника ЭДС

. Уберем ветвь с Z

. Тогда следующим контуром

будет состоять из источника ЭДС

и сопротивлений Z

, Z

Неизвестными контурными токами являются токи

во втором и

третьем контуре. Направления токов

выберем по часовой стрелке.

В итоге, уравнения для контурных токов имеют вид

⎪

⎩

⎪

⎨

⎧

+++++−=−++−−−=−

−−+=−−+=

.)()()()(

,)()(

3432003222340033300222

3200222130022211

IZZZIZZIZIZIIZIIIZE

IZIZIZZIIIZIZE

&&&&&&&&&&

&&&&&&&&

(3.22)

Решение этой системы приводит к выражениям для контурных токов:

))((

)(

243221

0042221432

ZZZZZZ

IZZEZEZZZ

−+++

+−++

&&&

(3.23a)

))((

)()(

243221

0032312122112

ZZZZZZ

IZZZZZZEZZEZ

−+++

++−+−

&&&

(3.23б)

Реальные токи в сопротивлениях получают из соотношений

3003

00322

IIIII

IIIIII

&&&&&

&&&&&&

=+=

−−==

(3.24)

Пример 3. Расчет методом узловых напряжений. Расчет выполним

для той же схемы, что и во втором примере (рис. 3.8). Вначале расчеты

проведем с использованием прямой записи системы канонических

уравнений. С этой целью будем считать ветви содержащие источники ЭДС

реальными источниками напряжения с внутренними сопротивлениями

соответственно Z

и Z

. Эти эффективные источники напряжения заменим

эквивалентными источниками тока. На рис. 3.9 приведен результат таких

эквивалентных преобразований:

1101

ZEI

4202

ZEI

. Выберем за

базисный узел нижний узел схемы. Потенциал этого узла равен нулю и от