Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.


70
Глава
2.
Математические
модели
вход-выход
h
K+-.-~~~---------
t
Рис.
2.10.
Переходная
функция
апериодического
звена
где
К
-
коэффициент
передачи,
Т
>
О
-
постоянная
времени,
а
=
l/Т,
Ь
==
=
!(
/Т.
Операторная
форма
звена
имеет
вид
или,
соответственно,
!(
Хl
=
Тр+
1
Х2
ь
Хl
=
--Х2.
р+а
Переходная
функция
звена
(рис.
2.10)
определяется
выражением
h(t) =
K(l
-
e-
tjТ
),
а
статическая
характеристика
-
(2.85)
(2.86)
(2.87)
(2.88)
Примерами
апериодических
звеньев
могут
служить
усилители
мощности,
тепловые
процессы,
процессы
разгона
двигателя,
RС-цепи
(см.
пример
1.1),
LR-цепи.
Интегрирующее
звено.
Звено
описывается
дифференци
альным
уравнением
или,
в
операторной
форме
-
к
Хl
=
-Х2·
Р
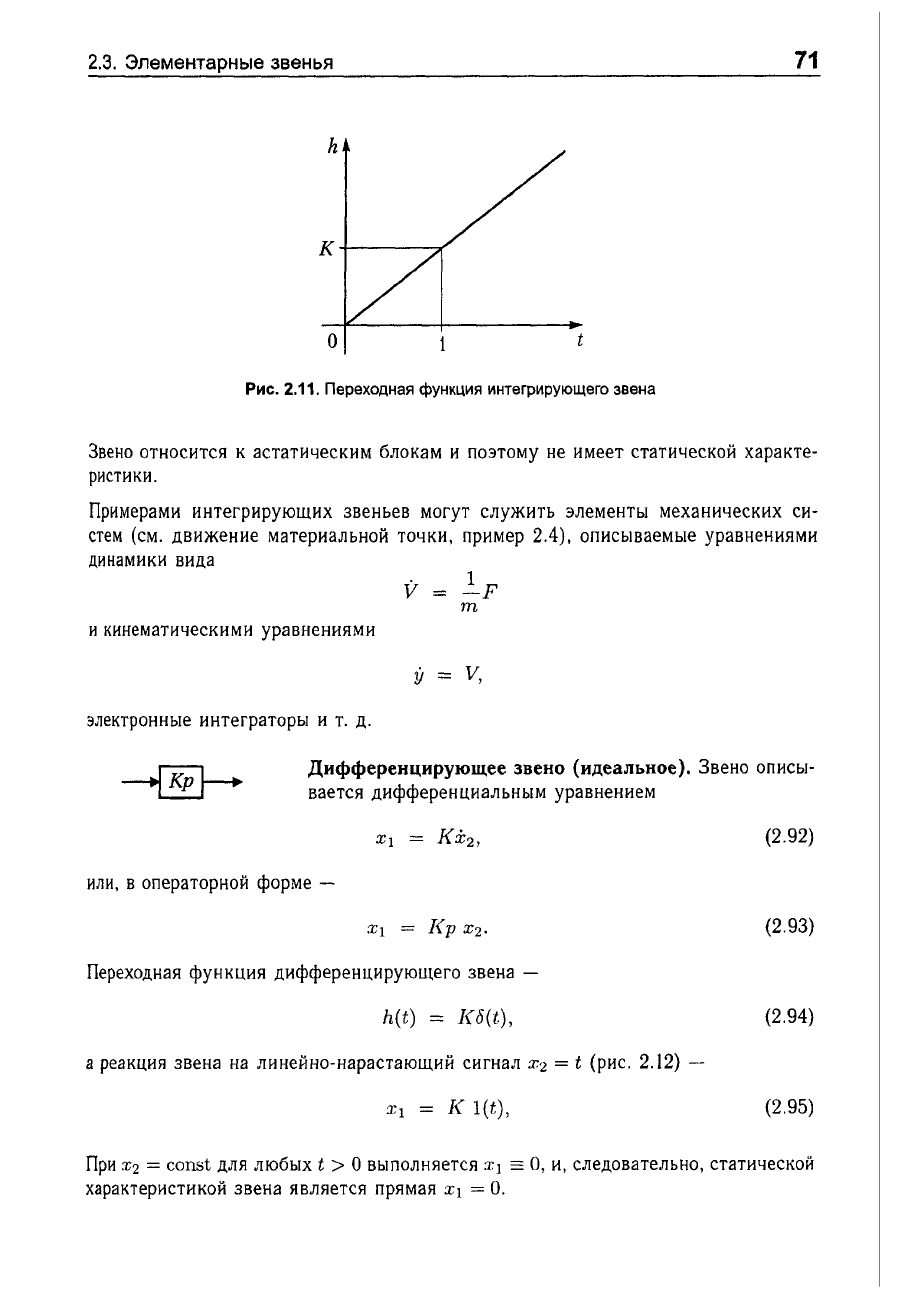
Переходная
функция
интегрирующего
звена
(рис.
2.11)
-
/l,(t)
=
Kt.
(2.89)
(2.90)
(2.91)
2.3.
Элементарные
звенья
71
h
K-+-----7I"
о
Рис.
2.11.
Переходная
функция
интегрирующего
звена
Звено
относится
к
астатическим
блокам
и
поэтому
не
имеет
статической
характе
ристики.
Примерами
интегрирующих
звеньев
могут
служить
элементы
механических
си
стем
(см.
движение
материальной
точки,
пример
2.4),
описываемые
уравнениями
динамики
вида
v =
J:..
p
m
и
кинематическими
уравнениями
у
=
V,
электронные
интеграторы
и
т.
д.
Дифференцирующее
звено
(идеальное).
Звено
описы
вается
дифференциальным
уравнением
(2.92)
или,
в
операторной
форме
-
(2.93)
Переходная
функция
дифференцирующего
звена
-
h(t) =
!(
8(t),
(2.94)
а
реакция
звена
на
линейно-нарастающий
сигнал
Х2
= t
(рис.
2.12)
-
Хl
=
к
l(t),
(2.95)
При
Х2
= const
для
любых
t >
О
выполняется
Хl
==
О, и,
следовательно,
статической
характеристикой
звена
является
прямая
Хl
=
О.

72
Глава
2.
Математические
модели
вход-выход
h
K+-----....---,..~---
о
Рис.
2.12.
Реакция
дифференцирующего
звена
на
линейно
нарастающее
воздействие
Примерами
дифференцирующих
звеньев
могут
служить
тахогенераторы
(электро
машинные
датчики
скорости),
электронные
ДИфференциаторы
и
т.
д.
Замечание
2.4.
При
К
= 1
выходом
дифференцирующего
звена
является
производ
ная
входного
сигнала,
т.
е.
его
мгновенная
скорость
dX2/dt.
Операция
нахождения
текущего
значения
скорости
Xl(t) = dX2(t)/dt
(только
по
информации
об
извест
ном
в
данный
момент
времени
t
сигнале
X2(t))
физически
не
реализуема,
и
поэтому
идеальных
дифференцирующих
звеньев
не
существует.
Тем
не
менее
производная
может
быть
приближенно
рассчитана
как
Хl
(t) =
дХ2(t)/
дt,
где
дt
-
интер
вал
времени,
дХ2
-
соответствующее
приращение
сигнала
Х2.
При
уменьшении
интервала
дt
можно
получить
значение
Хl
(t)
сколь
угодно
близкое
к
текущему
значению
скорости
Хl
(t).
Следовательно,
несмотря
на
нереализуемость
операции
дифференцирования
с
абсолютной
точностью,
возможно
построение
звена,
ко
торое
обеспечивает
сколь
угодно
точное
определение
производной
X2(t).
Реальное
дифференцирующее
звено.
Звено
описыва
ется
уравнением
или,
в
операторной
форме
-
Кр
Хl
=
Тр
+ 1
Х2·
Переходная
функция
звена
(рис.
2.13)
имеет
вид
h(t) =
~e-t/T,
(2.96)
(2.97)
(2.98)
а
реакция
звена
на
линейно
нарастающий
сигнал
Хl
= t
(рис.
2.14)
совпадает
с
переходной
функцией
апериодического
звена,
т.
е.
(2.99)
2.3.
Элементарные
звенья
73
h
к
о
т
t
п
=
3Т
t
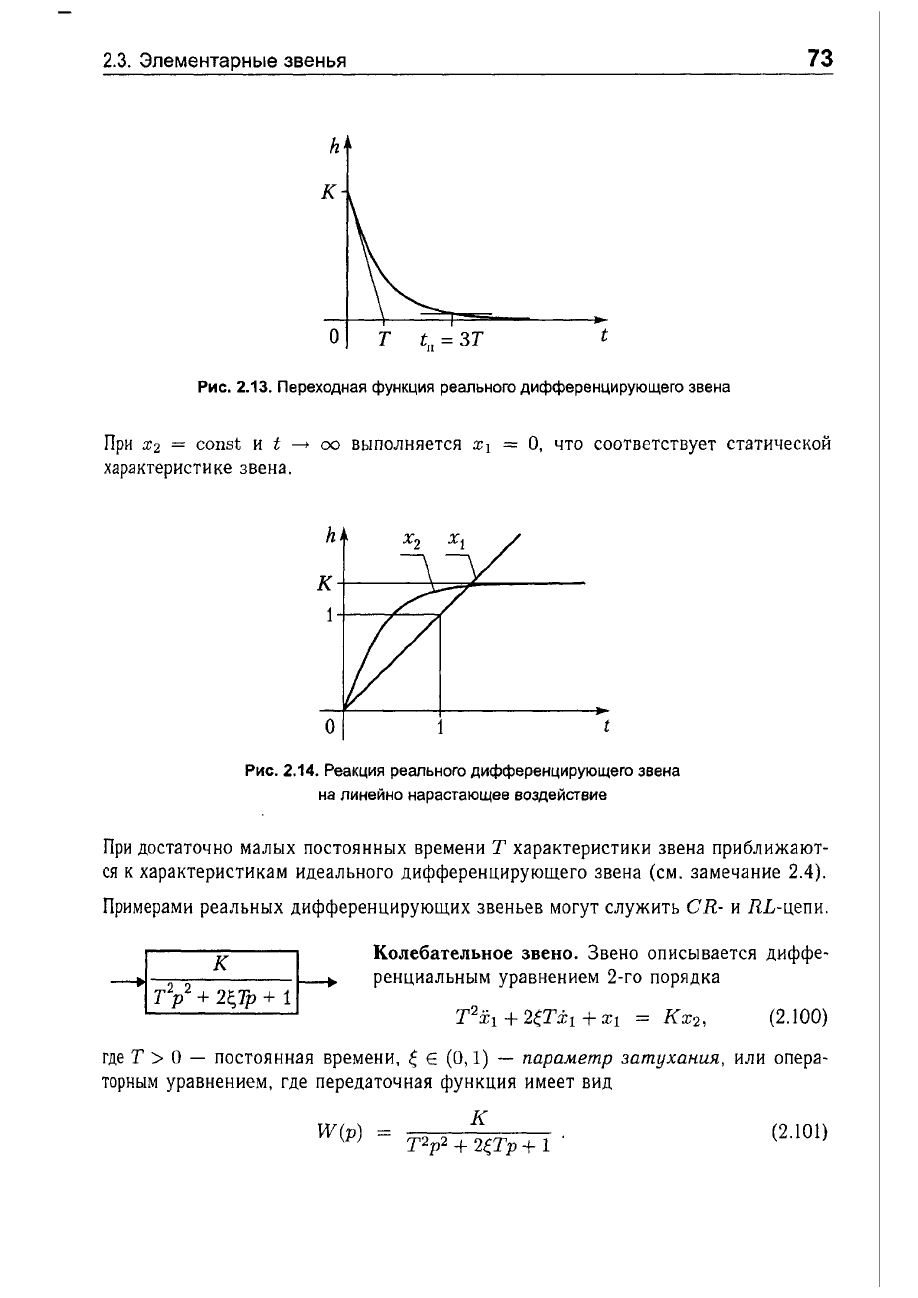
Рис.
2.13.
Переходная
функция
реального
дифференцирующего
звена
При
Х2
= const
и
t
~
00
выполняется
Хl
=
О,
что
соответствует
статической
характеристике
звена.
h
K+------+~~-------
о
Рис.
2.14.
Реакция
реального
дифференцирующего
звена
на
линейно
нарастающее
воздействие
При
достаточно
малых
постоянных
времени
Т
характеристики
звена
приближают
ся к
характеристикам
идеального
дифференцирующего
звена
(см.
замечание
2.4).
Примерами
реальных
дифференцирующих
звеньев
могут
служить
CR-
и
RL-цепи.
Колебательное
звено.
Звено
описывается
диффе
ренциальным
уравнением
2-го
порядка
(2.100)
где
Т
>
О
-
постоянная
времени,
~
Е
(0,1) -
параметр
затухания,
или
опера
торным
уравнением,
где
передаточная
функция
имеет вид
(2.101)

74
Глава
2.
Математические
модели
вход·выход
Корни
характеристического
уравнения
принимают
значения
~
.уТ=12
.
PI,2
=
-т
1=)
Т
=
а
1=)W,
где
cr
=
-~/T,
W =
уТ=12/Т
-
угловая
частота
колебаний.
h
о
t
Рис.
2.15.
Переходная
функция
колебательного
звена
Переходная
функция
звена
(рис.
2.15)
имеет
вид
h(t) =
](1
- Aoe-o:
t
sil1(wt
+
'РО)),
(2.102)
где
А
о
=
-11
+ a
2
/w
2
;
'Ро
= -arctg(w/cr) ,
а
статическая
характеристика
-
(2.103)
Примерами
колебательных
звеньев
могут
служить
маятниковые
системы
(в
вязкой
среде),
RLС-цепи
и
т.
д.
Замечание
2.5.
В
предельном
случае при
~
=
о на
выходе
звена
возникают
незз
тухающие
колебания,
а
при
~
= 1
имеет
место
монотонный
(апериодический)
процесс,
что
соответствует
рассматриваемым
далее
консервативному
и
двойному
апериодическому
звену.
Консервативное
звено
(осциллятор).
Звено
описывает
ся
дифференциальным
уравнением
(2.104)
или
операторным
уравнением,
где
W(p) =
!{
(2.105)

2.3.
Элементарные
звенья
75
и
получается
из
колебательного
звена
при
~
=
О.
Консервативное
звено
имеет
чисто
мнимые
полюсы
.1
.
Pl,2
=
=FJ
Т
=
=FJW
и
переходную
функцию
вида
(рис.
2.16)
h(t) =
/((1
- coswt),
(2.106)
где
U)
=
l/Т.
Звено
не
имеет
статической
характеристики.
h
о
t
Рис.
2.16.
Переходная
фУНКЦИЯ
консервативного
звена
Примерами
консервативных
звеньев
могут
служить
маятники
в
вакууме;
идеаль
ные
колебательные
(LC)
контуры
и
т.
д.
Двойное
апериодическое
звено.
Звено
описы
вается
уравнением
2-го
порядка
Т2Хl
+
2ТХl
+
Хl
=
/(
Х2
(2.107)
или
операторным
уравнением,
где
1
К
W
(Р)
=
Тр
+ 1
Тр
+ 1 .
(2.108)
Звено
имеет
равные
вещественные
корни
характеристического
уравнения
1
Рl,2
=
т
и
переходную
функцию
вида
(рис.
2.17)
/1(t)
=
К(l
-
e-
t
/
T
-
fe-t/T).
(2.109)
Статическая
характеристика
звена
-
(2.110)

76
Глава
2.
Математические
модели
вход-выход
h
K+-----~=-------------------
о
t
Рис.
2.17.
Переходная
функция
двойного
апериодического
звена
2.4.
Построение
моделей
вход-выход
Модель
вход-выход
системы
управления
строится
по
известным
уравнениям
от·
дельных
компонентов
(блоков,
звеньев,
см.
также
п.
4.3).
Процедура
сводится
к
преобразованию
системы
дифференциальных
уравнений,
описывающих
поведение
отдельных
блоков,
к
единому
уравнению
системы
управления
вида
(2.1),
(2.3)
или
(2.8).
При
этом
вне
зависимости
от
первоначального
описания
наиболее
удобной
для
осуществления
подобных
преобразований
является
операторная
форма
(2.8),
которая
по
окончании
процедуры
может
быть
легко
приведена
к
виду
(2.1)
или
(2.3).
2.4.1.
Простейшие
соединения
блоков
Рассмотрим
последовательное
соединение
блоков
(рис.
2.18),
т.
е.
систему,
опи
сываемую
операТОРНЫМI:i
уравнениями:
W
1
(p)X2,
W
2
(Р)ХЗ,
(2.111)
(2.112)
где,
соответственно,
Хl
=
Xl(t)
-
выходной,
а
Хз
=
.тз(t)
-
входной
сигналы
системы.
Рис.
2.18.
Последовательное
соединение
блоков
Требуется
найти
единое
описание
системы
(2.111)-(2.112),
т.
е.
уравнение
связи
сигналов
Хl
и
Хз.
Подставляя
(2.112)
в
(2.111),
получаем
(2.113)
2.4.
Построение
моделей
вход-выход
77
Таким
образом,
система
описывается
уравнением
Хl
=
W(р)хз,
(2.114)
где
-
передаточная
функция
системы
последовательно
соединенных
блоков.
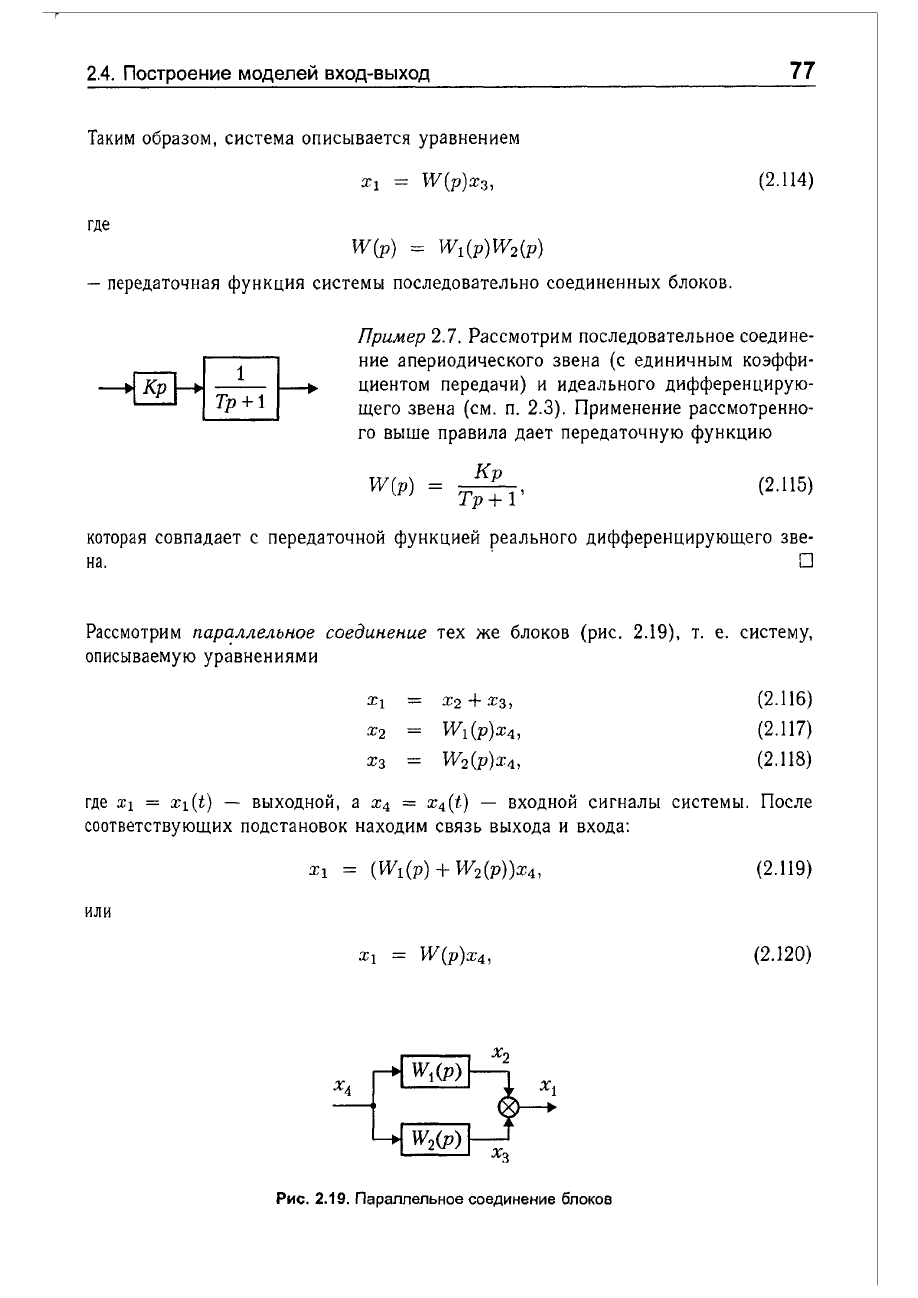
Пример
2.7.
Рассмотрим
последовательное
соедине
ние
апериодического
звена
(с
единичным
коэффи
циентом
передачи)
и
идеального
дифференцирую
щего
звена
(см.
п.
2.3).
Применение
рассмотренно
го
выше
правила
дает
передаточную
функцию
Кр
W(p) =
Тр+
l'
(2.115)
которая
совпадает
с
передаточной
функцией
реального
дифференцирующего
зве
на.
.
О
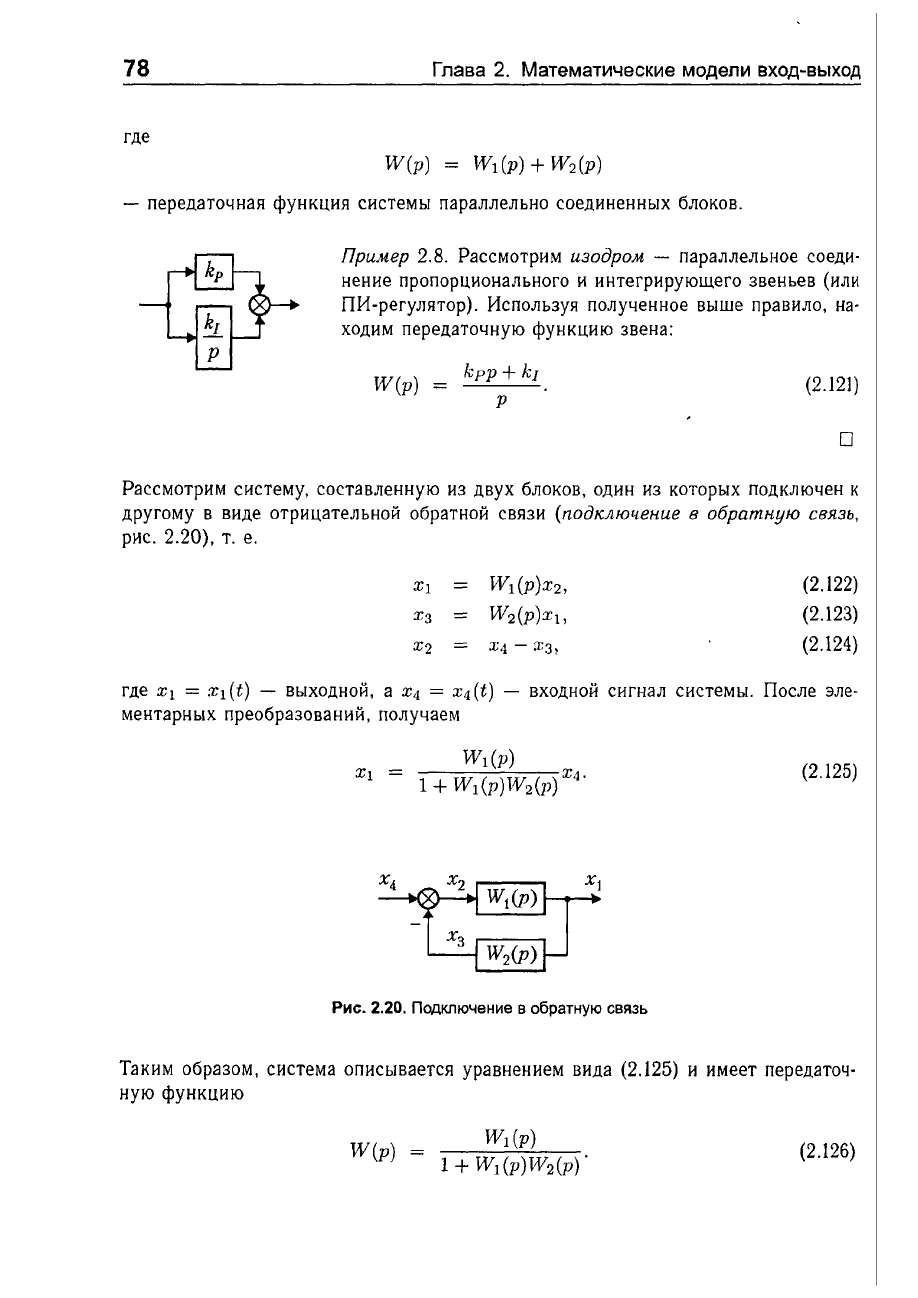
Рассмотрим
nаРG;ллелыюе
соединение
тех
же
блоков
(рис.
2.19),
т.
е.
систему,
описываемую
уравнениями
Хl
=
Х2
+
ХЗ,
Х2
W
1
(P)X4,
Хз
W
2
(P)X4,
(2.116)
(2.117)
(2.118)
где
Хl
=
Xl(t)
-
выходной,
а
Х4
= X4(t) -
входной
сигналы
системы.
После
соответствующих
подстановок
находим
связь
выхода
и
входа:
(2.119)
или
(2.120)
Рис.
2.19.
Параллельное
соединение
блоков
78
Глава
2.
Математические
модели
вход-выход
где
-
передаточная
функция
системы
параллельно
соединенных
блоков.
Пример
2.8.
Рассмотрим
изодром
-
параллельное
соеди
нение
пропорционального
и
интегрирующего
звеньев
(или
ПИ-регулятор),
Используя
полученное
выше
правило,
на
ходим
передаточную
функцию
звена:
W(p) = kpp + k]
р
(2.121)
о
Рассмотрим
систему,
составленную
из
двух
блоков,
один
из
которых
подключен
к
другому
в
виде
отрицательной
обратной
связи
(подключение
в
обратную
связь,
рис.
2.20),
т.
е.
Хl
= W
1
(Р)Х21
Хз
= W
2
(P)Xl,
(2.122)
(2.123)
(2.124)
где
Хl
=
Хl
(t) -
выходной,
а
Х4
=
Х4
(t) -
входной
сигнал системы.
После
эле
ментарных
преобразований,
получаем
(2.125)
Рис.
2.20.
Подключение
в
обратную
связь
Таким
образом.
система
описывается
уравнением
вида
(2.125)
и
имеет
передаточ
ную
функцию
W(p)
(2.126)

2.4.
Построение
моделей
вход-выход
79
Прuмер
2.9.
Рассмотрим
двойной
интегратор,
имеющий
передаточную
функцию
1 1 1
- - =
2'
р
р
р
с
отрицательной
обратной
связью,
образованной
пропорциональным
звеном
с
ко
эффициентом
",,2.
Используя
формулу
(2.125),
находим
(2.127)
где
К
=
1/~2
,
Т
=
l/~,
т.
е.
составной
блок
явля
ется
консервативным
звеном
(см.
п.
2.3).
О
Прuмер
2.10.
Рассмотрим
последовательное
соединение
пропорционального
звена
с
коЭффициентом
Ь
и
интегратора
l/р
с
отрицательной
обратной
связью
в
виде
пропорционального
блока
с
коэффициентом
а.
Используя
рассмотренные
выше
правила,
находим
ь
!(
W(p) =
р
+
а
=
Тр
+
l'
(2.128)
где
а
=
!(/Т,
Ь
=
l/I{,
Полученная
передаточ
ная
функция
соответствует
апериодическому
звену
(см.
п.
2.3),
О
Отметим,
что
для
системы
с
положительной
обратной
связью
уравнение
(2.124)
принимает
вид
(2.129)
и
С
другой
стороны,
в
простейшем
частном
случае,
когда
W
2
(p)
= 1
(единичная
отрицательная
обратная
связь),
получаем
2.4.2.
Передаточные
функции
систем
управления
Сначала
рассмотрим
систему
управления
без
обратной
связи
-
так
называемую
разомкнутую
систему,
СОСТОЯЩУIQ
из
последовательно
соединенных
регулятора
