Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.

60
Глава
2.
Математические
модели
вход-выход
2.2.1.
Переходные
процессы
Решением,
дифференциального
уравнения
(2.1)
называется
функция
()
(
. (n-l))
yt
= yt,yO,YO,
...
,yo ,
(2.44)
которая
при
t =
О
удовлетворяет
начальным
условиям,
а
для
любых
t
Е
[О,
t
f)
-
уравнению
(2.1).
С
этим определением
тесно
связано
понятие
фазовых
nерем,енных
систем,ы,
к
которым
относятся
функции
y(t), i;(t),
...
, y(n-l)(t),
удовлетворяющие
ура~нению
(2.1),
и
понятие
переходного
процесса.
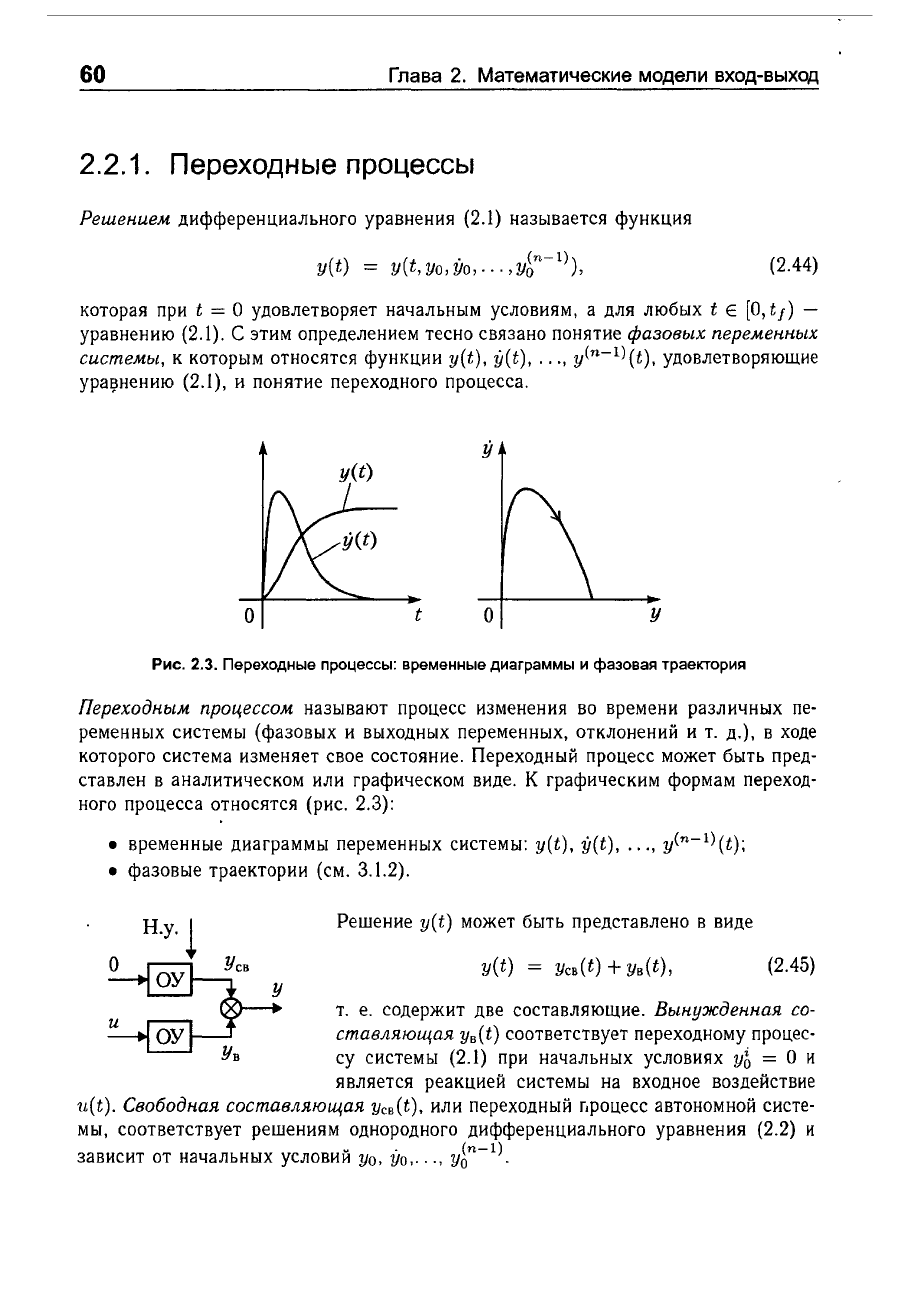
y(t)
о
t
о
у
Рис.
2.3.
Переходные
процессы:
временные
диаграммы
и
фазовая
траектория
Переходным,
nроцессом,
называют
процесс
изменения
во
времени
различных
пе
ременных
системы
(фазовых
и
выходных
переменных,
отклонений
и
т.
д.),
В
ходе
которого
система
изменяет
свое
состояние.
Переходный
процесс
может
быть
пред
ставлен
в
аналитическом
или
графическом
виде.
К
графическим
формам
переход
ного
процесса
относятся
(рис.
2.3):
•
временные
диаграммы
переменных
системы:
y(t), i;(t),
...
, y(n-l)(t);
•
фазовые
траектории
(см.
3.1.2).
H'Y'l
у
Решение
y(t)
может
быть
представлено
в
виде
y(t) =
YCB(t)
+
YB(t),
(2.45)
т.
е.
содержит
две
составляющие.
Вынужденная
со
ставляющая
ув
(t)
соответствует
переходному
процес
су
системы
(2.1)
при
начальных
условиях
уь
=
О
и
является
реакцией
системы
на
входное
воздействие
u(t).
Свободная
составляющая
YCB(t),
или
переходный
Гlроцесс
автономной
систе
мы,
соответствует
решениям
однородного
дифференциального
уравнения
(2.2)
и
u • (n-l)
зависит
от
начальных
условии
уо,
Уа,·
..
,
Уо
.
2.2.
Переходные
процессы
и
характеристики
моделей
вход-выход
61
2.2.2.
Процессы
автономных
систем
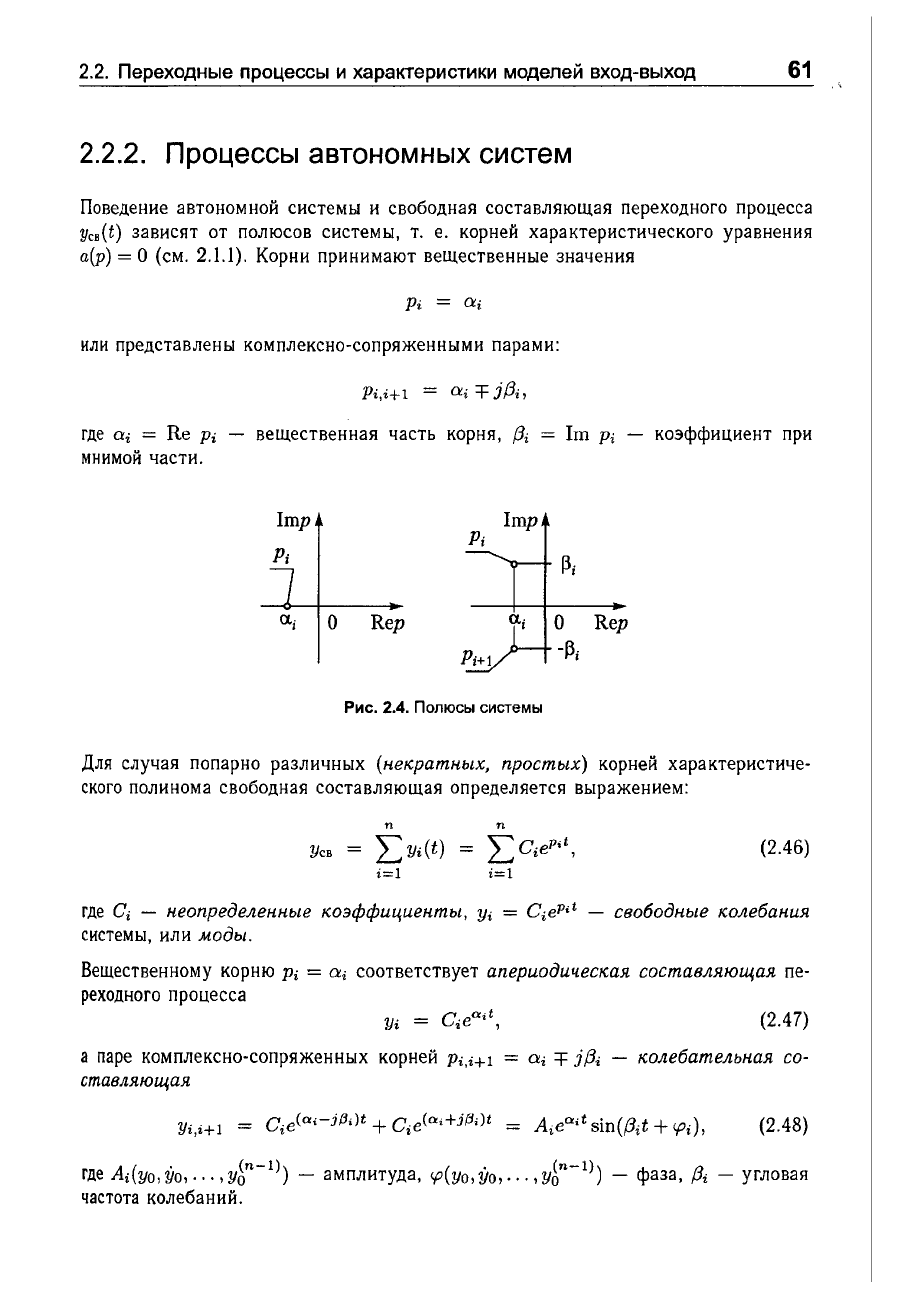
Поведение
автономной
системы
и
свободная
составляющая
переходного
процесса
YCB(t)
зависят
от
полюсов
системы,
т.
е.
корней
характеристического
уравнения
а(р)
=
О
(см.
2.1.1).
Корни
принимают
вещественные
значения
или
представлены
комплексно-сопряженными
парами:
где
ач
=
Re
Pi
мнимой
части.
вещественная
часть
корня,
f3i
=
1т
Pi -
коэффициент
при
Imp
Р;
Imp
Pi
~;
о,;
О
Rep
О
Rep
-~i
Рис.
2.4.
Полюсы
системы
Для
случая
попарно
различных
(некратных,
простых)
корней
характеристиче
ского
полинома
свободная
составляющая
определяется
выражением:
n n
Усв
=
LYi(t)
=
LCiePit,
(2.46)
i=l
i=l
где
C
i
-
неоnределенные
коэффициенты,
Yi
=
Cie
Pit
-
свободные
колебания
системы,
или
м,оды.
Вещественному
корню
Pi
=
Qi
соответствует
апериодическая
составляющая
пе
реходного
процесса
(2.47)
а
паре
комплексно-сопряженных
корней
Pi,i+l
=
Qi
=F
jf3i -
колебательная
со
ставляющая
(2.48)
А
(
.
(n-l))
('
(n-l))
Ф
f3
где
i
Уа,
Уа,
...
'Уа
-
амплитуда,
<р
Уа,
Уа,
...
'Уа
-
аза,
i -
угловая
частота
колебаний.
,\
62
Глава
2.
Математические
модели
вход-выход
УЦ+1
о
t
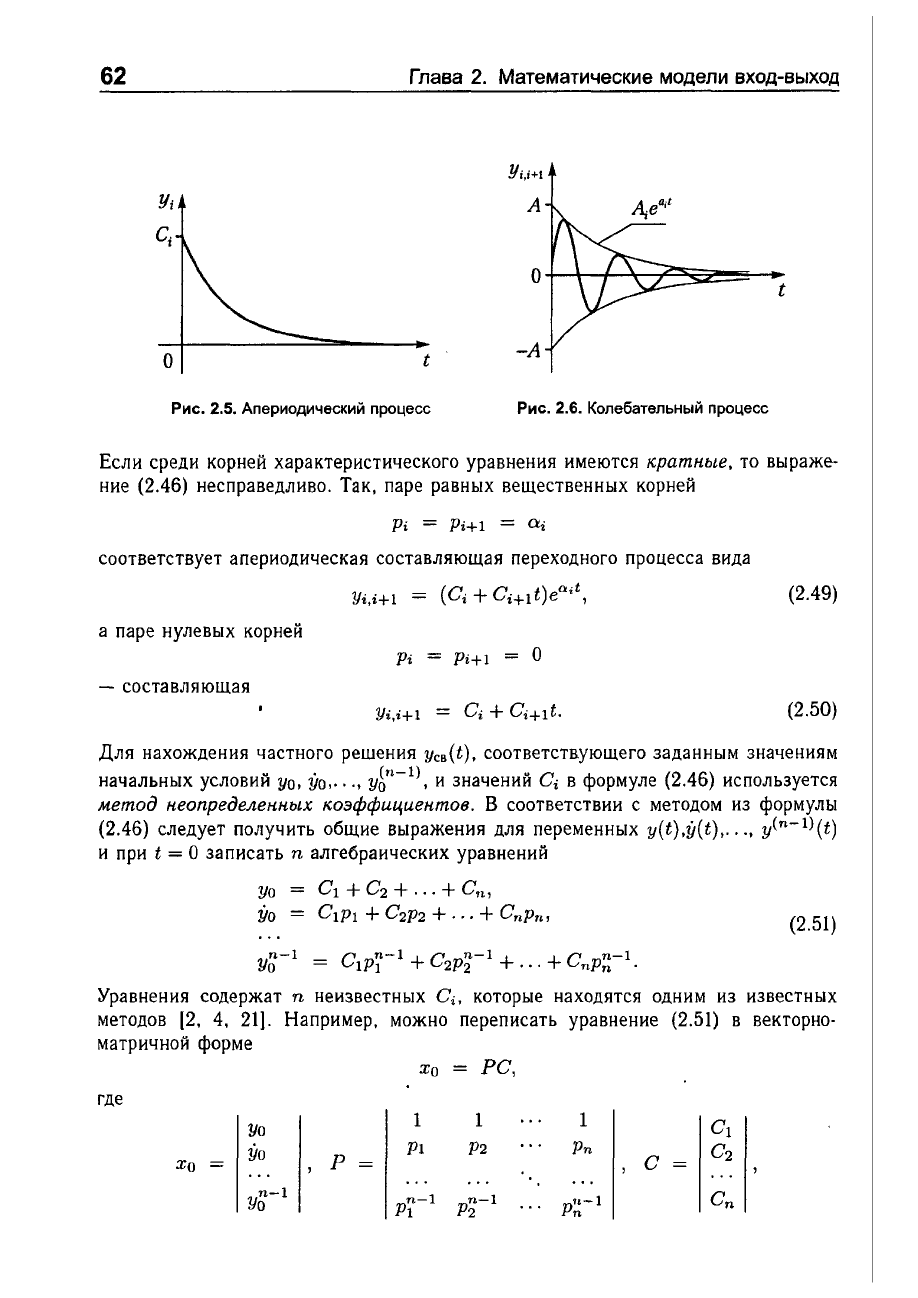
Рис.
2.5.
Апериодический
процесс
Рис.
2.6.
Колебательный
процесс
Если
среди
корней
характеристического
уравнения
имеются
кратные,
то
выраже
ние
(2.46)
несправедливо.
Так,
паре
равных
вещественных
корней
соответствует
апериодическая
составляющая
переходного
процесса
вида
Yi,i+1 =
(C
i
+ Ci+1t)eQit,
а
паре
нулевых
корней
Pi =
РН1
=
О
-
составляющая
(2.49)
(2.50)
Для
нахождения
частного
решения
YCB(t),
соответствующего
заданным
значениям
начальных
условий
Уо, Уо,
.
..
,
уа
n
-
1
),
и
значений
C
i
в
формуле
(2.46)
используется
м,етод
неоnределенных
коэффициентов.
В
соответствии
с
методом
из
формулы
(2.46)
следует
получить
общие
выражения
для
переменных
Y(t),y(t),
...
,
y(n-1)(t)
и
при
t =
О
записать
n
алгебраических
уравнений
Уо
=
С
1
+
С
2
+ ... +
сп,
уо
=
С
1
Р1
+
С
2
Р2
+ ... +
СnРn,
(2.51)
y~-1
=
C1p~-1
+
C2p~-1
+ ... +
Cnp~-1.
Уравнения
содержат
n
неизвестных
C
i
,
которые
находятся
одним
из
известных
методов
[2,
4,
21].
Например,
можно
переписать
уравнение
(2.51)
в
векторно
матричной
форме
Ха
=
РС,
где
Уо
1
1
1
С
1
Уо
Р
Р1
Р2
Рn
С
2
ХО
=
,
,
с
n-1
n-1
n-1
p~-1
Сп
Уо
Р1
Р2

2.2.
Переходные
процессы
и
характеристики
моделей
вход-выход
63
и
найти
вектор-столбец
неизвестных
коэффициентов
как
,
-1
С
=
Р
Хо.
Если
при
некоторых
начальных
значениях
имеет
место
тождество
Уев
=
у*,
t
~
О,
где
у*
= const,
то
значение
У
=
у*
называется
равновесным
значением
выход
ной
переменной
или
просто
положением
равновесия
автономной
системы
(2.2).
В
положении
равновесия
можно
записать
*.
о
(n)
Уев
=
У,
Уев
= , ... ,
Уев
О.
(2.52)
После
подстановки
(2.52)
в
уравнение
(2.2)
найдем
(2.53)
При
условии,
что
а
n
=f:.
О,
находим,
что
единственным
положением
равновесия
рассматриваемой
системы
является начало
координат
у*
=
О,
(2.54)
а
при
а
n
=
О
можно
получить
бесчисленное
множество
равновесных
значений.
Замечание
2.1.
При
условии,
что
вещественная
часть
Re
Pi
= D:i
некоторого
корня
Pi
строго
отрицательна,
т.
е.
Re
Pi
<
О,
(2.55)
соответствующая
мода
со
временем
затухает:
Нт
Yi(t) =
О.
t--->oo
Если
условие
(2.55)
имеет
место
для
всех
корней
(i =
г,n),
то
затухающей
явля
ется
свободная
составляющая
переходного
процесса
в
целом:
Нm
YeB(t)
=
О,
t--->oo
(2.56)
причем
предельное
значение
выходной
переменной
в
точности
совпадает
с
поло
жением
равновесия
автономной
системы
у*
=
О.
2.2.3.
Вынужденное
движение
Вынужденная
составляющая
переходного
процесса
YB(t)
зависит
от
входного
воз
действия и
может
быть
аналитически
определена
только
для
ряда
частных
случаев,
64
Глава
2.
Математические
модели
вход-выход
соответствующих
некоторым
типовым
входным
сигналам
[4,21].
Наиболее
распро
страненными
сигналами
являются
единичный
скачок,
дельта-функция
и
гармони
ческое
входное
воздействие.
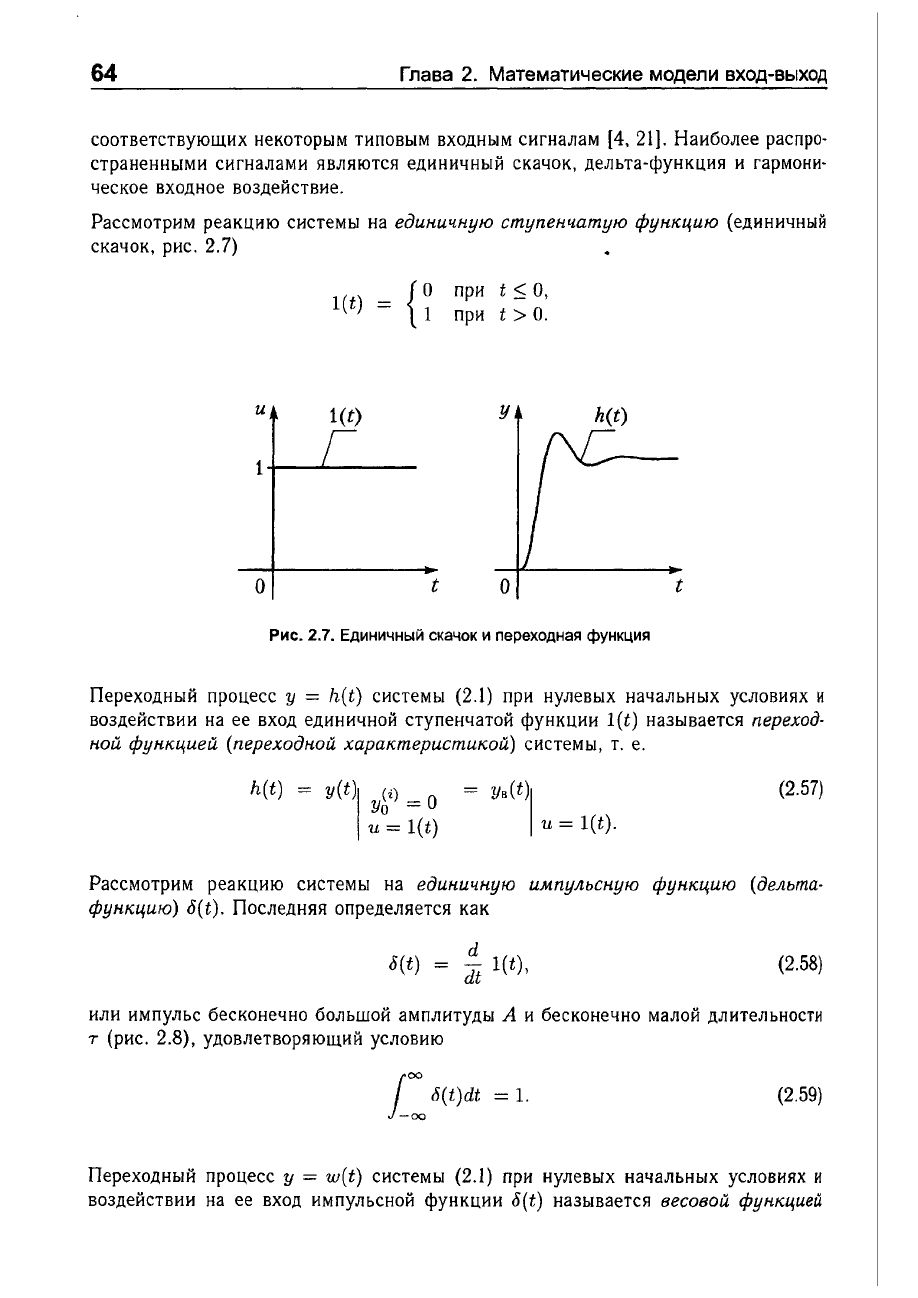
Рассмотрим
реакцию
системы
на
единичную
ступенчатую
функцию
(единичный
скачок,
рис.
2.7)
l(t)
=
{~
u
1(t)
1+--""'"-----
о
t
при
t
~
о,
при
t>
о.
у
о
h(t)
Рис.
2.7.
Единичный
скачок
и
переходная
функция
t
Переходный
процесс
у
= h(t)
системы
(2.1)
при
нулевых
начальных
условиях
и
воздействии
на
ее
вход
единичной
ступенчатой
функции
l(t)
называется
переход
ной
функцией
(переходной
характеристикой)
системы,
т.
е.
h(t) =
y(t)1
(i)
Уа
=
О
и
=
l(t)
=
YB(t)1
и
=
l(t).
(2.57)
Рассмотрим
реакцию
системы
на
единичную
импульсную
функцию
(дельта
функцию)
б(t).
Последняя
определяется как
d
б(t)
= dt
l(t),
(2.58)
или
импульс
бесконечно
большой
амплитуды
А
и
бесконечно
малой
длительности
т
(рис.
2.8),
удовлетворяющий
условию
[:
д(t)dt
=
1.
(2.59)
Переходный
процесс у
= w(t)
системы
(2.1)
при
нулевых
начальных
условиях
и
воздействии
на
ее
вход
импульсной
функции
б(t)
называется
весовой
функцией
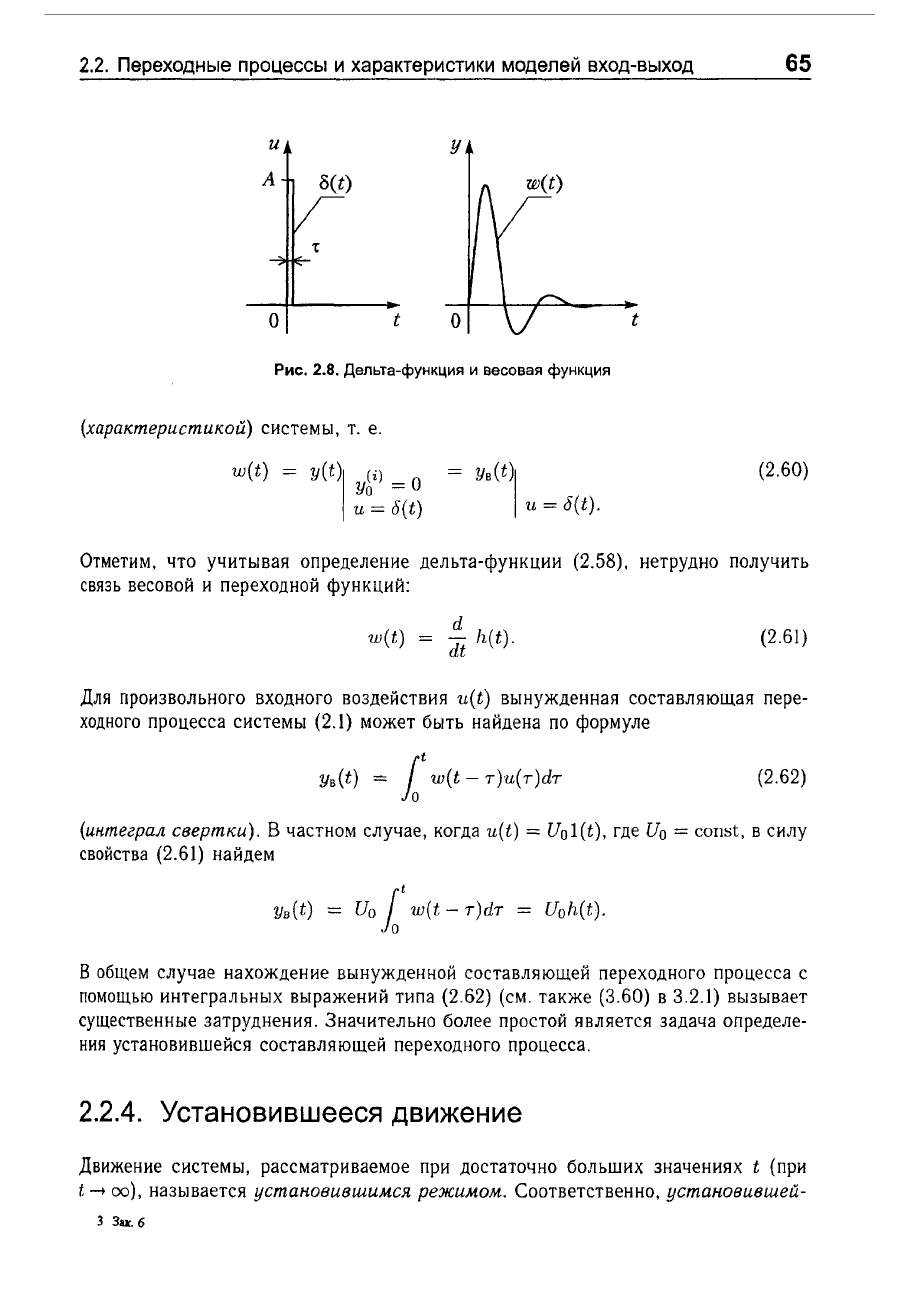
2.2.
Переходные
процессы
и
характеристики
моделей
вход-выход
65
u
у
А
8(t)
о
t
о
t
Рис.
2.8.
Дельта-функция
и
весовая
функция
(характеристикой)
системы,
т.
е.
w(t) =
y(t)1
(i)
Уа
=
О
и
=
б(t)
=
YB(t)1
и
=
б(t).
(2.60)
Отметим,
что
учитывая
определение
дельта-функции
(2.58),
нетрудно
получить
связь
весовой
и
переходной
функций:
d
w(t) =
dt
/1(t).
(2.61)
Для
произвольного
входного
воздействия
u(t)
вынужденная
составляющая
пере
ходного
процесс
а
системы
(2.l)
может
быть
найдена
по
формуле
YB(t)
=
l'
w(t - r)'U(r)dr
(2.62)
(интеграл
свертки).
В
частном
случае,
когда
u(t) = U
a
l(t),
где
U
а
= const,
в
силу
свойства
(2.61)
найдем
YB(t)
=
И
О
l'
w(t -
r)dr
=
Иоlt(t).
в
общем
случае
нахождение
вынужденной
составляющей
переходного
процесса
с
помощью
интегральных
выражений
типа
(2.62)
(см.
также
(З.60)
в
З.2.1)
вызывает
существенные
затруднения.
Значительно
более
простой
является
задача
определе
ния
установившейся
составляющей
переходного
процесса.
2.2.4.
Установившееся
движение
Движение
системы,
рассматриваемое
при
достаточно
больших
значениях
t
(при
t --+
00),
называется
установивши,М,ся
режи'м'О'м'.
Соответственно,
установившей-
3
Заж.6
66
Глава
2.
Математические
модели
вход-выход
ся
составляющей
переходного
процесса
Yy(t)
называется
вынужденная
составля
ющая
YB(t)
при
t
-+
00,
т.
е.
Yy(t) =
liш
YB(t).
t--+OO
(2.63)
Последнее
выражение
предполагает
существование
предела
функции
YB(t).
В
более
общем
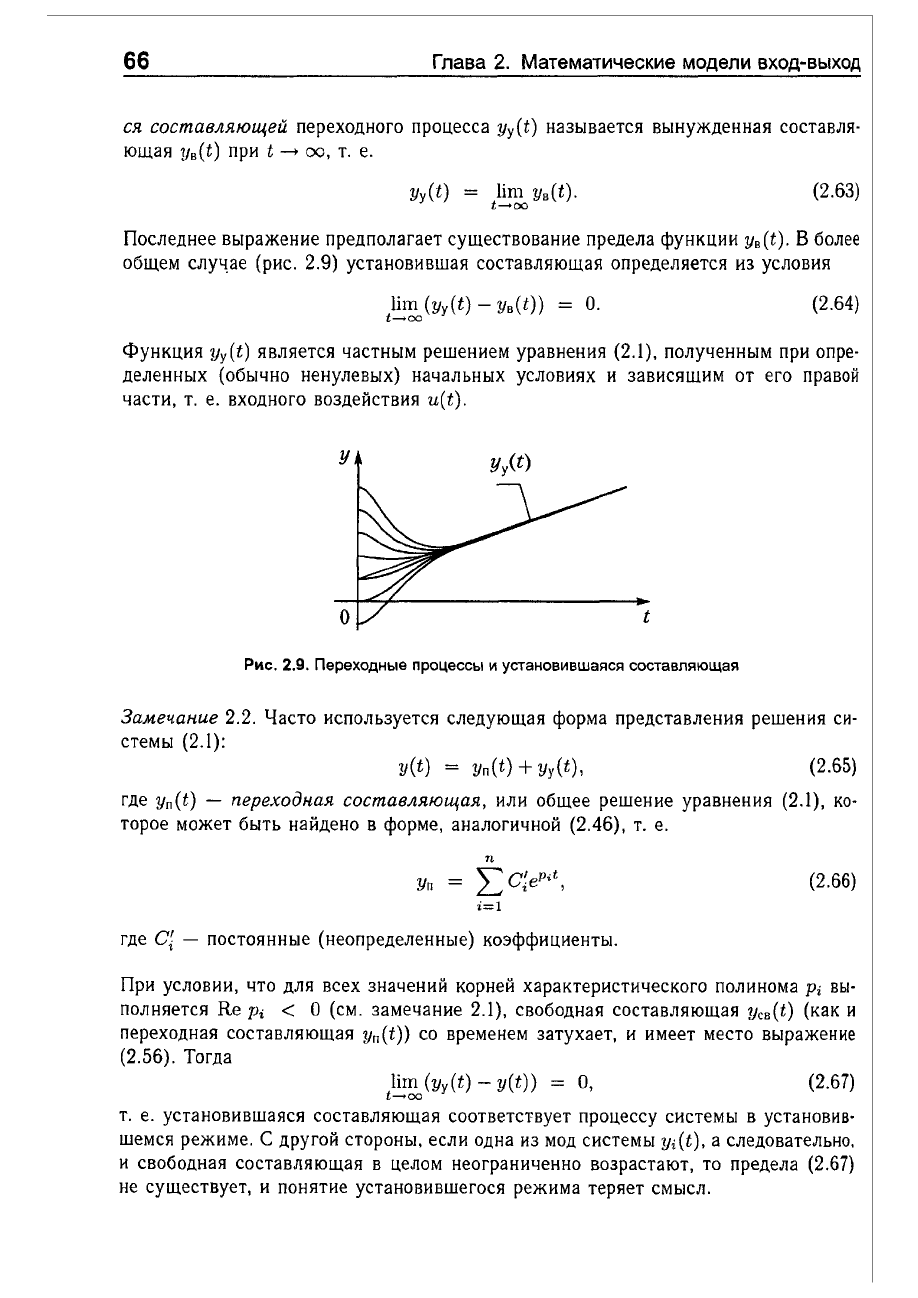
слу~ае
(рис.
2.9)
установившая
составляющая
определяется
из
условия
liш
(Yy(t) -
YB(t»
=
О.
t--+oo
(2.64)
Функция
Yy(t)
является
частным
решением
уравнения
(2.1),
полученным
при
опре
деленных
(обычно
ненулевых)
начальных
условиях
и
зависящим
от
его
правой
части,
т.
е.
входного
воздействия
u(t).
у
о
t
Рис.
2.9.
Переходные
процессы
и
установившаяся
составляющая
Замечание
2.2.
Часто
используется
следующая
форма
представления
решения
си
стемы
(2.1):
y(t) = yn(t) + Yy(t),
(2.65)
где
yn(t) -
nереходная
составляющая,
или
общее
решение
уравнения
(2.1),
ко
торое
может
быть
найдено
в
форме,
аналогичной
(2.46),
т.
е.
n
Уп
= L C:e
Pit
,
i=l
где
С:
-
постоянные
(неопределенные)
коэффициенты.
(2.66)
При
условии,
что
для
всех
значений
корней
характеристического
полинома
Pi
вы
полняется
Re
Pi
<
О
(см.
замечание
2.1),
свободная
составляющая
YCB(t)
(как
и
переходная
составляющая
yn(t)
СО
временем
затухает,
и
имеет
место
выражение
(2.56).
Тогда
liш
(Yy(t) - y(t») =
О,
t--+oo
(2.67)
т.
е.
установившаяся
составляющая
cOOTBeTC'FByeT
процессу
системы
в
установив
шемся
режиме.
С
другой
стороны,
если
одна
из
мод
системы
Yi(t),
а
следовательно.
и
свободная
составляющая
в
целом
неограниченно
возрастают,
то
предела
(2.67)
не
существует,
и
понятие
установившегося
режима
теряет
смысл.

2.2.
Переходные
процессы
и
характеристики
моделей
вход-выход
67
Типовые
частные
решения
линейного
уравнения
(2.1),
соответствующие
установив
шимся
составляющим
переходного
процесса
при
воздействии
на
систему
типовых
входных
сигналов
u(t),
находятся
по
известным
правилам:
и
У
у
U
о
У
О
U
о
+ U
1
t
У
О
+ Y
1
t
U
о
sinwt
У
О
sin(wt +
<р)
где
U
о
,
U
1
,
УО,
У
1
,
w,
<р
-
постоянные.
2.2.5.
Статический
режим
Наиболее
важный
частный
случай
решения
системы
(2.1)
соответствует
постоян
ному
входному
воздействию
u =
U
о
=
COl1st
и
установившейся
составляющей
у
=
У
О
=
COl1st.
(2.68)
Пусть
свободная
составляющая
системы
затухает,
т.
е.
имеет
место
свойство
(2.67)
и,
следовательно,
liш
y(t) =
Уу.
t->oo
Последняя
формула
показывает,
что
при
достаточно
больших
t
в
системе
отсут
ствует
движение,
т.
е.
имеет
место
статический
режим
работы.
Решение
уравнения
(2.1)
в
статическом
режиме
ищется
в
виде
Уу
=
к
и,
(2.69)
где
К
-
неопределенный
коэффициент.
С
учетом
того,
что
при
t >
О
u =
U
о
=
= const,
запишем
U(i)
=
О,
i = 1, n -
1,
а
из
уравнения
(2.69)
найдем,
что
ут
=
О,
i =
г,n.
(2.70)
(2.71)
После
подстановки
(2.70)-(2.71)
в
(2.1)
получим
простое
алгебраическое
выраже-
ние
Пусть а
n
=1=
О.
Тогда
коэффициент
!<
находится
как
!(
=
Ь
т
а
n
(2.72)
(2.73)

68
Глава
2.
Математические
модели
вход-выход
При
а
n
=
О
получим
Ьти
=
О
,
где
(см.
п.
2.1)
Ь
т
=1-
О,
т.
е.
в
этом
случае
(2.69),
вообще
говоря,
не
является
частным
решением
уравнения
(2.1).
Зависимость
установившейся
составляющей
(выходной
переменной
после
оконча
ния
переходного
процесса)
Уу
от
величины
входного
сигнала
u = const
называется
статической
характеристикой
динамической
системы.
Для
линейных
систем
ви
да
(2.1)
статическая
характеристика
представлена
уравнением
прямой
(2.69),
где
постоянная
К,
рассчитываемая
по
формуле
(2.73),
называется
коэффициентом
передачи,
или
статическим
коэффициентом
системы.
u
Система
(2.1),
для
которой
а
n
=1-
О
и,
следователь
но,
существует
статическая
характеристика,
называ
ется
статической
системой.
Астатической
называется
система,
для
которой
а
n
=
=
О
и,
следовательно,
статической
характеристики
не
существует,
а
установившийся
режим
невозможен
(см.
также
п.
6.4).
Нахождение
статической
характеристики
сводится
к
элементарной
операции
расчета
статического
коэффициента
К
по
формуле
(2.73),
где
а
n
И
Ь
т
-
соответствующие
коэффициенты
дифференциального
уравнения
(2.1).
Вместе
с
тем
статическая
характеристика
может
быть
получена
и из
опера
торной
формы
(2.3)
или
(2.8).
Сопоставляя
(2.73)
и
(2.8),
находим
Ь
т
=
к
=
W(O)
=
Ь(О)
.
а
n
а(О)
(2.74)
Следовательно,
в
статическом
режиме
система
описыва
ется
уравнением
Уу
= W(O)u.
(2.75)
Замечание
2.3.
По
аналогии
с
определением
положения
равновесия
автономной
системы
(2.2)
можно
ввести
понятие
равновесия
системы
(2.1)
при
постоянном
входном
воздействии
u =
и
о
= const,
т.
е.
положения,
в
котором
выполняется
тождество
y(t) =
у*
= const
и,
следовательно,
y(i)
=
О,
i =
г,n.
(2.76)
Нетрудно
показать,
что
равновесное
значение
у*
выходной
переменной
у
в
точно
сти
совпадает
с
установившимся
значением,
т.
е.
у*
=
Уу
= const.
(2.77)
В
частном
случае
при
u =
О
получаем
автономную
систему
(2.2)
и
равновесное
положение
у*
=
Уу
=
О.

2.3.
Элементарные
звенья
69
2.3.
Элементарные
звенья
Элементарными
звеньями
называюТся
простейшие
со
ставные
части
(блоки)
системы,
поведение
которых
опи
сывается
алгебраическими
уравнениями
или
дифферен
циальными
уравнениями
1-2-ro
порядков
(см.
также
[4, 39]):
(2.78)
где
Хl
= Xl(t) -
выходная
переменная,
Х2
=
X2(t)
-
входная
переменная,
ai,
b
i
-
постоянные
коэффициенты
(параметры).
Уравнение
(2.78)
можно
записать
в
операторной
форме:
Ь
1
Р
+
Ь
2
(2.79)
т.
е.
передаточная
функция
элементарного
звена
имеет
вид
(2.80)
Пропорциональное
(безынерционное)
звено.
Звено
опи
сывается
алгебраическим
уравнением
(2.81)
где
К
-
коэффициент
передачи
(nроnорциональности).
Уравнение
(2.81)
в
силу
отсутствия
у
блока
инерционных
свойств
совпадает
со
статической
характеристи
кой.
Переходная
функция
пропорционального
звена
-
h(t) =
Kl(t).
(2.82)
Примерами
пропорциональных
звеньев
могут
служить
измерительные
потенцио
метры,
редукторы,
усилители
напряжения
и
т.
д.
Апериодическое
звено.
Звено
описывается
дифферен
циальным
уравнением
(2.83)
или,
в
приведенной
форме
-
уравнением
(2.84)
